УДК 537.874; 621.3.095
Применение плоской металлической проволочной решетки для измерения диэлектрических параметров материалов
И. П. Никитин, Е. Е. Чигряй
Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья поступила в редакцию 10 марта 2016 г.
Аннотация. Предлагается модификация стандартной методики измерения диэлектрических свойств материалов в КВЧ диапазоне, которая основана на использовании электродинамических свойств плоских металлических проволочных решеток. С помощью таких решеток удается применить методы, основанные на измерении характеристик пропускания и отражения диэлектрической пластины, к исследованию жидких диэлектриков, а также модифицировать методику, основанную на измерении коэффициента отражения от плоской диэлектрической пластины.
Ключевые слова: диэлектрические свойства, КВЧ диапазон, решетки из металлической проволоки, интерференционная картина.
Abstract. A modification of the method for measuring the dielectric properties of materials in the EHF band is proposed. It is based on the application of the electromagnetic properties of plane wire grids. Using these grids, one can apply the methods based on the measurement of reflection and transmission characteristics of a dielectric plate to the study of liquid dielectric materials, as well as modify the method based on measuring the reflection coefficient of a plane dielectric plate.
Key words: dielectric properties, EHF band, wire grids, interference pattern.
1. Введение
В последние десятилетия изучение диэлектрических свойств твердых и жидких веществ в диапазоне крайне высоких частот (КВЧ), включающем миллиметровый и субмиллиметровый диапазоны длин волн, привлекало значительное внимание исследователей. В немалой степени этот интерес обусловлен тем, что измерение частотной зависимости комплексной диэлектрической проницаемости материалов позволяет получить важную информацию о физических процессах, происходящих в диэлектриках, полупроводниках, сегнетоэлектриках и ферритах. Кроме того, очень часто измерение диэлектрической проницаемости полимеров, керамик, различных композиционных материалов, а также многих бытовых и строительных материалов позволяет оценивать такие характеристики материалов, как химический состав, влажность, содержание примесей, и т.п. С другой стороны, знание диэлектрических характеристик материалов в КВЧ диапазоне необходимо для разработки различных функциональных элементов для систем радиовидения, неразрушающего контроля, интроскопии и локальной коммуникации, работающих в этом диапазоне.
Наиболее распространенным методом исследования диэлектриков является определение комплексной диэлектрической проницаемости e = e' - ie'' (или комплексного показателя преломления n* = n - ik). Для этого измеряют коэффициенты пропускания и/или отражения слоя исследуемого материала в зависимости от частоты падающей волны (рис. 1). В случае изотропного однородного диэлектрика коэффициенты пропускания и отражения нормально падающей линейно поляризованной волны выражаются следующими стандартными формулами:
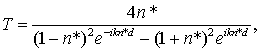 (1)
(1)
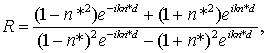 (2)
(2)
где ![]() , l0 - длина волны в
вакууме и d толщина слоя материала.
, l0 - длина волны в
вакууме и d толщина слоя материала.
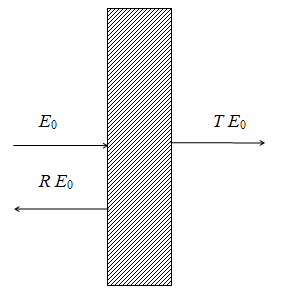
Рис. 1. Плоскопараллельная диэлектрическая пластина.
Стрелки
указывают направление падающей, прошедшей и отраженной волн.
Информация о свойствах диэлектрика может быть получена из анализа частотной зависимости коэффициентов |T|2 и |R|2. В качестве иллюстрации на рис. 2 представлены частотные зависимости коэффициента отражения |R|2 слоя диэлектрика толщиной d = 0.6 cm с e' = 2.5, рассчитанные при различных значения тангенса угла потерь tgd = e'/ e''. Показатель преломления и показатель поглощения материала, связанные с действительной и мнимой частями диэлектрической проницаемости по формулам
e' = n2 - k2, e'' = 2nk,
могут быть рассчитаны по измеренным значениям коэффициента отражения и пропускания в зависимости от частоты при различных значениях других параметров диэлектрического слоя. Например, показатель преломления можно легко определить по измерению разности частот между экстремумами интерференционной картины (см. рис. 2). Для более точного определения n применяются интерференционные методы на основе интерферометров Рождественского или Майкельсона. Для определения показателя поглощения k применяют разные методы в зависимости от толщины образца и параметров материала. Эти методы сводятся к измерению коэффициента ослабления a = 2pk/l и достаточно подробно изложены в [1, 2].

Рис. 2. Частотная зависимость коэффициента пропускания
пластины диэлектрика с e'
= 2.5 и толщиной d = 0.6 см,
рассчитанная при
различных значения тангенса угла потерь: tgd = 10-3 (кривая 1), 10-2 (2) и 10-1 (3)
.
К сожалению, описанная выше методика измерения характеристик диэлектриков сталкиваются со значительными трудностями в случае жидких диэлектриков. Прежде всего это связано с тем, что невозможно создать образец в виде плоскопараллельного слоя из жидкого материала. Поэтому приходится исследовать коэффициенты пропускания и отражения измерительной кюветы, содержащий слой исследуемого жидкого диэлектрика, где присутствие дополнительных слоев (стенок кюветы) усложняет методику и увеличивает погрешность измерений, либо приходится ограничиваться измерением коэффициента отражения от поверхности жидкости, предварительно исключив влияние отражения от дна сосуда, содержащего жидкость.
В данной работе,мы предлагаем небольшую модификацию вышеописанной методики измерений, которая заключается в использовании плоской решетки из металлической проволоки.
2. Решетки из металлических проводников
Периодические структуры из проводящих стержней находят многообразные применения в радиофизике и электронике. Плоские решетки, представляющие собой периодическую систему параллельных тонких проводящих нитей или проволок широко применяются в СВЧ и КВЧ диапазонах в качестве поляризаторов и делителей волновых пучков. Подробный обзор, а также обширная библиография по теории проволочных решеток представлены в [4]. В работе подчеркивается, что в большинстве случаев, когда период решетки и диаметр проволоки много меньше длины волны, проволочные решетки можно считать идеально отражающими для линейно поляризованной плоской волны с электрическим вектором, параллельным осям проволок, и не влияющими на прохождение этой волны в случае, когда электрический вектор перпендикулярен осям проволок. Весьма широкий класс периодических структур, а также строгий электродинамический анализ таких структур проведен в [3]. С теоретической точки зрения решетку из проволочных структур можно рассматривать как анизотропно проводящую поверхность. Оказалось [5], что на основе таких поверхностей можно создавать ряд структур, обладающих уникальными электродинамическими характеристиками, интересными для создания элементов и устройств СВЧ и КВЧ диапазонов. В частности, было показано [5], что такие структуры могут обладать резонансными свойствами даже в случае, когда их размеры малы по сравнению с длиной волны.
В настоящей работе мы рассматриваем простейший вид анизотропно проводящей поверхности - плоскую проволочную решетку. Если считать, что такая решетка практически не влияет на прохождение волны, поляризованной перпендикулярно к направлению осей проволок, а волна, поляризованная параллельно проволокам, полностью отражается от решетки, то в случае, когда электрический вектор падающей волны направлен под углом q к направлению проволок, коэффициенты пропускания и отражения имеют вид
![]() ,
, ![]() (3)
(3)
где q - величина угла между направлением электрического вектора падающей волны и направлением осей проволок. Следует, однако, отметить, что формулы (3) не учитывают поляризацию прошедшей и отраженной волн, т.е., направления поляризации прошедшей и отраженной волн не совпадают с направлением поляризации падающей волн. В экспериментах по исследованию свойств диэлектриков обычно имеют дело с фиксированным направлением поляризации. Поэтому коэффициенты пропускания и отражения при фиксированном направлении поляризации принимают вид
![]() ,
, ![]() (4)
(4)
2.1. Исследование жидких диэлектриков с использованием проволочных решеток.
Поскольку свободная проволочная решетка является проницаемой для жидкостей, то, помещая такую решетку в жидкость параллельно плоскости поверхности на расстоянии d от поверхности, можно создать вторую границу и таким образом применить методику измерения плоскопараллельной пластины к исследованию жидких диэлектриков (см. рис. 3).
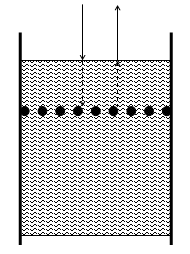
Рис. 3. Схема измерения коэффициента отражения от жидкого диэлектрика с погруженной в него решеткой.
В таком случае коэффициент отражения от поверхности жидкости, с погруженной в нее проволочной решеткой имеет вид
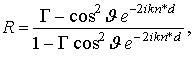 (5)
(5)
где
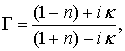 (6)
(6)
представляет собой комплексный коэффициент отражения от границы вакуум-диэлектрик, а d - глубина погружения решетки (расстояние от поверхности жидкости до плоскости решетки). Измеряя расстояние между минимумами функции |R|2, можно определить показатель преломления жидкости, а варьирую величину d и измеряя связанное с этим изменение максимумов, можно вычислить коэффициент поглощения k. Существуют и другие методы извлечения характеристик диэлектрика из измеренной частотной зависимости |R|2, которые можно легко реализовать в данном случае [1, 2]. В частности, применение проволочной решетки позволяет легко осуществить переход от режима закороченного слоя при q = 0, когда коэффициент отражения имеет вид
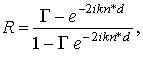 (7)
(7)
к режиму отражения от свободной границы, когда R = G, простым поворотом решетки вокруг оси, перпендикулярной плоскости решетки. К сожалению, в данной конфигурации трудно обеспечить точные измерения коэффициента пропускания. Поэтому в настоящей статье мы ограничимся анализом коэффициента отражения, который дает достаточно полную информацию для определения параметров диэлектриков.
В качестве иллюстрации на рис. 4 представлены частотные зависимости коэффициента отражения по мощности (|R|2) от структуры, изображенной на рис. 3, при e' = 2.5, q = 0, d = 0.6 см и различных значениях диэлектрических потерь tgd = e''/e' (кривые 1 - 3 соответствуют значениям tgd = 10-3, 10-2 и 10-1, соответственно. Верхняя пунктирная кривая соответствует материалу без потерь (tgd = 0) при q = 0, а нижняя - при q = 90 (т.е., коэффициенту отражения от свободной поверхности жидкости). Можно видеть, что коэффициент отражения очень сильно зависит от потерь в диэлектрике, что делает возможным определение параметров последнего путем измерения коэффициента отражения с помощью стандартных методов, описанных в [2]. Из рисунка также видно, что при малых потерях (кривая 1) глубина интерференции мала, что может привести ошибкам в измерении действительной части e (или n). В данной ситуации применение проволочной решетки позволяет легко преодолеть эту трудность. На рис. 4 представлены частотные зависимости коэффициента отражения в схеме рис. 5 при tgd = 10-3 для разных значений q: q = 0 (кривая 1) q = (кривая 2) и q = (кривая 3). Из рисунков видно, что изменяя угол q, можно существенно усилить резкость интерференционной картины и таким образом увеличить точность определения показателя преломления.
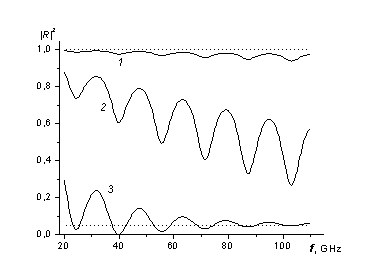
Рис. 4. Частотная зависимость коэффициента отражения,
измеренная в схеме рис. 3 при e'
= 2.5, q
= 0, d = 0.6 см
различных значениях
диэлектрических потерь tgd = e''/e'
(кривые 1 - 3
соответствуют значениям tgd = 10-3,
10-2 и 10-1).
Верхняя пунктирная прямая -
коэффициент отражения при tgd = 0 и q = 0, а нижняя
пунктирная прямая - при q = 90о.
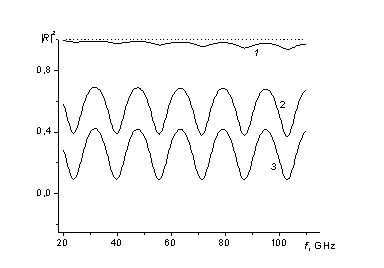
Рис. 5. Частотная зависимость коэффициента отражения,
измеренная в схеме рис. 3
при e'
= 2.5, tgd
= 10-3, d = 0.6 см и различных значениях угла q:
q = 0 (кривая 1), 30о (2)
и 45о (3). Пунктирная прямая - коэффициент отражения при tgd
= 0 и q =
0.
2.2. Применение проволочных решеток для исследования твердых диэлектриков.
Благодаря своим поляризационным свойствам проволочные решетки могут оказаться весьма полезными при исследовании твердых диэлектриков путем измерения коэффициентов отражения и пропускания плоскопараллельной пластины. В данном случае к тыльной поверхности пластины вплотную прикладывается проволочная решетка (рис. 6).

Рис. 6. Диэлектрическая пластина с проволочной решеткой.
Коэффициент отражения от такой структуры имеет вид
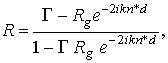 (8)
(8)
где
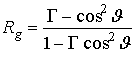 (9)
(9)
коэффициент отражения линейно поляризованной волны, падающей со стороны образца
на тыльную поверхность с решеткой. Из последней формулы видно, Rg обращается в нуль
при G = cos2q, т.е. при угле q между направлением
поляризации падающей волны и направлением осей проволок равном ![]() . В случае диэлектрика с e' = 2.5, этот угол равен
примерно 61.7о. Иными словами, при q = 61.7o отражение от второй границы
структуры отсутствует, что проявляется в сглаживании интерференционной картины (пунктирная
прямая на рис. 7). Происходит как бы "просветление" границы. Однако,
следует иметь в виду, что эффект просветления имеет место только для заданной
поляризации. На самом деле отраженная волна присутствует; однако, она имеет
ортогональную поляризацию и не учитывается в измерительной установке,
работающей при фиксированной поляризации. Указанный эффект может быть
использован для грубой но быстрой оценки величины e'. Измеряя угол, при которой исчезает
интерференционная картина, по формуле G
= cos2q в
пренебрежении k можно оценить величину n.
. В случае диэлектрика с e' = 2.5, этот угол равен
примерно 61.7о. Иными словами, при q = 61.7o отражение от второй границы
структуры отсутствует, что проявляется в сглаживании интерференционной картины (пунктирная
прямая на рис. 7). Происходит как бы "просветление" границы. Однако,
следует иметь в виду, что эффект просветления имеет место только для заданной
поляризации. На самом деле отраженная волна присутствует; однако, она имеет
ортогональную поляризацию и не учитывается в измерительной установке,
работающей при фиксированной поляризации. Указанный эффект может быть
использован для грубой но быстрой оценки величины e'. Измеряя угол, при которой исчезает
интерференционная картина, по формуле G
= cos2q в
пренебрежении k можно оценить величину n.
Однако, основным достоинством метода, использующего проволочную решетку, является то, что она позволяет повысить глубину интерференционной картины, а также чувствительность коэффициента отражения от потерь в диэлектрике; последние определяют точность определения действительной и мнимой частей комплексного показателя преломления. Для иллюстрации на рис. 7 и 8 в одинаковом масштабе представлены частотные зависимости коэффициента отражения от структуры, изображенной на рис. 6 при различных значениях потерь при q = 90o, что эквивалентно отсутствию решетки (рис. 7), и при q = 30o (рис. 8).
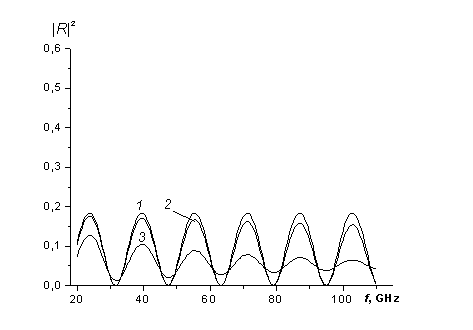
Рис. 7. Частотная зависимость коэффициента отражения,
измеренная в схеме рис. 6
при e'
= 2.5, q
= 90о, d = 0.6 см и
различных значениях диэлектрических потерь tgd = e''/e'
(кривые 1 -
3 соответствуют значениям tgd = 10-3,
10-2 и 10-1).

Рис.
8. То же, что на рис. 7 при q = 90о. Пунктирная прямая - коэффициент
отражения при q = 61.7о,
когда отражение от дальней границы
образца отсутствует.
Сравнение рис. 7 и 8 показывает, что с помощью проволочной решетки удается не только существенно увеличить глубину интерференции, но также в 2-3 раза усилить зависимость коэффициента отражения на максимуме от величины потерь в материале, что позволяет значительно повысить точность определения параметров материала.
3. Заключение
Таким образом, с помощью численных расчетов продемонстрировано, что применение проволочных решеток позволяет модифицировать стандартные методики определения параметров диэлектриков путем измерения коэффициентов отражения и пропускания плоскопараллельной пластины из исследуемого материала. Полученные результаты показывают, что модифицированная методика дает возможность существенно повысить точность определения параметров материалов.
Литература
1. В.В. Мериакри, В.Н. Аплеталин, А.Н. Копнин, Г.А. Крафтмахер, М.Г. Семенов, Е.Ф. Ушаткин, Е.Е. Чигряй, Субмиллиметровая лучеводная спектроскопия и ее применения, в сб. Успехи современной радиотехники и электроники, под ред. В.А. Котельникова, М: Наука, 1980.
2. В.В. Мериакри, Исследование диэлектриков, сегнетоэлектриков и ферритов на субмиллиметровых волнах, Дисс. докт. физ.-мат. наук, ИРЭ РАН, Москва, 1973.
3. Е.И. Нефедов, А.Н. Сивов, Электродинамика периодических структур, М.: Наука, 1977.
4. T. Larsen, A survey of the theory of wire grids, IRE Trans. Microwave Theory Tech., 1962, MTT-10, no. 3, pp 191-201.
5. И.П. Коршунов, Е.Н. Коршунова, А.Н. Сивов, А.Д. Шатров, "Частотно-селективные экраны, излучающие и волноведущие структуры на основе анизотропно проводящих поверхностей", Радиотехника и электроника, 2007, т. 52, №4, с. 389-402.