|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2002 |
|
СТРУКТУРА СПЕКТРА КВАЗИПЕРИОДИЧЕСКОГО КОЛЕБАНИЯ В СИСТЕМЕ СВЯЗАННЫХ НЕЛИНЕЙНЫХ ОСЦИЛЛЯТОРОВ
В. В. Копытов, К. С. Костенко.
E-mail: softmaster@pisem.net
Филиал Ростовского военного института РВ (г. Ставрополь)
Получена 20 мая 2002 г.
Оценена структура энергетического спектра квазипериодического колебания возникающего в системе связанных нелинейных осцилляторов с внешним гармоническим воздействием при переходе к хаосу через бифуркации удвоения периода частоты биений между осцилляторами
1.введение
Переходам к хаотическому движению через квазипериодические колебания в нелинейных распределенных системах и средах, как известно, предшествуют режимы усложняющейся автомодуляции. Бифуркационные явления рождения хаоса при разрушении квазипериодических колебаний реализуются и исследуются при периодическом внешнем воздействии на устойчивый предельный цикл автономных систем, в системах двух взаимодействующих нелинейных осцилляторов, а также в автономных нелинейных и распределенных системах, способных работать в режимах автомодуляции. В этом случае, согласно модели Рюэля-Такенса [1], переход к хаотическому движению становится возможным после двух бифуркаций Хопфа и сопровождается нелинейными процессами разрушения фазового портрета в виде двумерного тора. В результате в окрестности исходного тора возникает стохастическое множество – тор-аттрактор, эволюционирующий далее к развитому хаосу. Спектр колебаний обогащается новыми и комбинационными частотами, увеличивается их число и интенсивности, растет число гармоник, и в итоге спектр становится сплошным, свидетельствуя о нерегулярности колебаний. Однако экспериментальные исследования показали, что в связанных неавтономных нелинейных системах под внешним воздействием наблюдается переход к хаосу через бифуркации удвоения периода одного из движений на двумерном торе при изменении внешнего управляющего параметра, подобно каскаду удвоений периода Фейгенбаума [2]. Явления возникающие в данных системах существенно отличаются от модели перехода к турбулентности по Рюэлю-Такенсу и требуют проведения дополнительных исследований.
Целью работы является определение структуры энергетического спектра сложнопериодического колебания возникающего при переходе к хаосу в системе связанных неавтономных нелинейных динамических систем.
2. ОСНОВНЫЕ МОДЕЛЬНЫЕ СООТНОШЕНИЯ
Рассмотрим формирование энергетического спектра хаотического сигнала в системе связанных нелинейных осцилляторов в виде подобных связанных колебательных контуров (рис. 1) с внешним гармоническим воздействием, каждый из которых содержит нелинейную емкость с вольт-фарадной характеристикой показанной на рисунке 2.
Рис. 1. Система связанных нелинейных колебательных контуров
Рис. 2. Вольт-фарадная характеристика нелинейной емкости
Для решения задачи оценки прохождения сигнала от входного контура к выходному используют в качестве передаточной функции взаимное сопротивление между контурами, при этом выражение для амплитудно-частотной характеристики напряжения на вторичном контуре определяется следующим образом [3]
где ![]() - взаимное сопротивление между контурами; R1, R2 – значения
активных сопротивлений каждого контура; k – коэффициент связи катушек индуктивности; Q – добротность;
- взаимное сопротивление между контурами; R1, R2 – значения
активных сопротивлений каждого контура; k – коэффициент связи катушек индуктивности; Q – добротность; ![]() - обобщенная расстройка; wр(U) - резонансная частота
нелинейного контура зависящая от напряжения на контуре.
- обобщенная расстройка; wр(U) - резонансная частота
нелинейного контура зависящая от напряжения на контуре.
При значении коэффициента связи соответствующему
критическому значению ![]() напряжение
на вторичном контуре принимает максимальное значение
напряжение
на вторичном контуре принимает максимальное значение ![]() . Дальнейшему увеличению
коэффициента связи амплитудно-частотной характеристике соответствует двугорбая
форма, максимальные значения которой соответствуют двум значениям резонансных
частот w01,2, разность частот между которыми определяется
как
. Дальнейшему увеличению
коэффициента связи амплитудно-частотной характеристике соответствует двугорбая
форма, максимальные значения которой соответствуют двум значениям резонансных
частот w01,2, разность частот между которыми определяется
как
Предельно допустимое значение
коэффициента связи kпр
ограничено требованием, чтобы полоса пропускания связанных контуров не
содержала разрывов, т.е. ![]()
При внешнем воздействии на систему с нелинейными элементами энергетический спектр реакции системы оказывается дискретным, содержащим составляющие с частотами, кратными частоте вынуждающего сигнала. Рассмотрим формирование дискретного спектра в системе связанных нелинейных колебательных контуров при внешнем гармоническом воздействии с частотой w0.
Полагая добротность контура
достаточно большой, можно ожидать, что при протекании через контур тока с
частотой w0 напряжение на контуре будет
синусоидальным той же частоты ![]() даже, если ток i содержит еще и гармоники частоты w0. Ток в емкостной ветви определяется выражением
даже, если ток i содержит еще и гармоники частоты w0. Ток в емкостной ветви определяется выражением
где ![]() - дифференциальная емкость
p-n перехода. В результате
получаем
- дифференциальная емкость
p-n перехода. В результате
получаем
Аппроксимируя относительно смещения в рабочей точке зависимость С(и), показанную на рисунке 2, полиномом второй степени
с положительными коэффициентами С0, а1, а2 и подставляя (5) в (4) получаем
Из данного выражения видно наличие трех гармоник тока с частотами w0, 2w0, 3w0 с различными начальными фазами, причем первая и третья гармоники имеют одинаковую амплитуду и противоположные начальные фазы.
При значениях коэффициента связи k > kкр в системе связанных нелинейных колебательных контуров с увеличением величины входного тока I1 возникают колебания представляющие суперпозицию двух биений, обусловленных характером начальных условий (наличием энергии в первичном и вторичном контурах). Закономерности обоих биений одинаковы: уменьшение амплитуды колебаний в одном контуре сопровождается ростом ее в другом и наоборот, т.е. происходит перераспределение энергии между контурами. Процесс повторяется периодически с частотой биений, под которой подразумевают величину
В результате при превышении коэффициента связи критического значения в данной нелинейной системе возникают как гармоники частоты внешнего воздействия w0, 2w0,…, iw0,…, так и гармоники частоты биений W, 2W,…, jW,…, приводящие к амплитудной автомодуляции частоты внешнего воздействия, что соответствует фазовому портрету в виде двумерного тора. Проекция фазового портрета и осциллограмма сигнала во вторичном контуре при возникновении биений между нелинейными контурами показаны на рисунке 3.
Рис. 3. Проекция фазового портрета а) и осциллограмма напряжения во вторичном контуре б) при возникновении биений между нелинейными контурами (физический эксперимент)
Результирующий сигнал во вторичном контуре в случае, если частота внешнего воздействия совпадает с резонансной частотой контуров w0, определяется как
где UjW, F0j – амплитуда напряжения и начальная фаза j-ой гармоники частоты биений соответственно; j0i – начальная фаза i-ой гармоники напряжения внешнего воздействия во вторичном контуре.
Спектральный состав данного сигнала в области первой гармоники частоты внешнего воздействия с учетом первых трех гармоник частоты биений показан на рисунке 4.
Рис.4 Спектральный состав сигнала во вторичном контуре при возникновении
биений между нелинейными контурами
Определим энергетический спектр сигнала с учетом полосы пропускания системы. Для попадания комбинационных частот w0±W в полосу пропускания при предельном значении коэффициента связи должно выполнятся следующее условие [3]
Учитывая, что при
предельном значении коэффициента связи ![]() , получаем
, получаем ![]() . Это показывает, что комбинационные
составляющие уже от первой гармоники частоты биений находятся за пределами
полосы пропускания системы.
. Это показывает, что комбинационные
составляющие уже от первой гармоники частоты биений находятся за пределами
полосы пропускания системы.
Уровень подавления второй гармоники частоты вынуждающего воздействия 2w0 (значение расстройки x=2) определяется следующим отношением
![]()
При значении добротности Q = 10 и kпрQ = 2,41 уровень второй гармоники частоты внешнего воздействия будет составлять 0,013U2max. Следовательно, в энергетическом спектре системы будут присутствовать комбинационные частоты только от первой гармоники частоты воздействия и частоты биений.
При значении коэффициента связи kкр < k < kпр изменение значения внешнего управляющего параметра, которым в данном случае является частота внешнего воздействия, приводит к последовательности бифуркаций удвоения периода частоты биений и вблизи точки перехода приближено моделируется следующим одномерным отображением
где l - управляющий параметр; р – целое число.
Частота биений, являясь модулирующим сигналом частоты внешнего воздействия в результате бифуркаций удвоения периода, обладает сложным спектральным составом. Моделью такого сигнала является тригонометрическая функция
где частоте W0 соответствует значение частоты биений (7). В случае амплитудной автомодуляции задающего воздействия результирующее колебание во вторичном контуре примет вид
Определим значения
амплитуд ![]() возникающих
в результате бифуркаций удвоения периода частоты биений используя бифуркационную
диаграмму системы описываемой одномерным отображением (10). Как следует из самоподобия элементов цикла
[2] значения управляющего параметра ln в точке n-ой бифуркации при больших n ведут себя как геометрическая прогрессия с постоянной
d
возникающих
в результате бифуркаций удвоения периода частоты биений используя бифуркационную
диаграмму системы описываемой одномерным отображением (10). Как следует из самоподобия элементов цикла
[2] значения управляющего параметра ln в точке n-ой бифуркации при больших n ведут себя как геометрическая прогрессия с постоянной
d
![]() ,
,
где l¥ - значение управляющего параметра в точке возникновения статистической необратимости колебаний в системе.
Отношение расстояний dn/dn+1, где dn - расстояния по оси Х между ![]() и ближайшим к нему
элементом цикла при l = ln, также имеет предел равный
постоянной a [2]. При
увеличении в a раз вблизи
и ближайшим к нему
элементом цикла при l = ln, также имеет предел равный
постоянной a [2]. При
увеличении в a раз вблизи ![]() очередная бифуркация
будет выглядеть точно так же, как и предыдущая. Значения постоянных a и d в зависимости от показателя степени р в
выражении (10) приведены в табл. 1
[4].
очередная бифуркация
будет выглядеть точно так же, как и предыдущая. Значения постоянных a и d в зависимости от показателя степени р в
выражении (10) приведены в табл. 1
[4].
Таблица 1
|
р |
a |
d |
|
р |
a |
d |
|
1,0 2,0 3,0 4,0 5,0 |
2,5029 1,9277 1,6903 1,556 1,468 |
4,6692 6,0847 7,2851 8,345 9,31 |
|
6,0 7,0 8,0 9,0 10,0 |
1,405 1,35 1,32 1,29 1,27 |
10,18 10,98 11,72 12,48 13,15 |
Энергетический спектр стохастических колебаний при l < l¥ дискретный, так как колебания периодические, а при l > l¥ содержит как дискретные составляющие, так и шумовые. Расчет дискретного энергетического спектра в бифуркационной области с использованием самоподобия элементов цикла показал, что для l-ой Фурье-амплитуды при (n +1)-ой бифуркации удвоения
где ![]() - решение после (n +1)-ой бифуркации; Тn+1 – период данного решения;
- решение после (n +1)-ой бифуркации; Тn+1 – период данного решения;
вблизи точки l¥ выполняется универсальный закон подобия [2]
где
т. е. амплитуды нечетных субгармоник, которые появляются в результате каждой бифуркации, в среднем равны усредненным амплитудам старых нечетных компонент, помноженным на постоянное число g-1. Фурье – амплитуды для четных субгармоник остаются неизменными при всех последующих бифуркациях
Схематично изменение фурье-компонент в результате двух бифуркаций представлено на рисунке 5.
Следовательно, при бифуркациях удвоения, когда 2n- цикл переходит в 2n+1- цикл в спектре мощности процесса мягко рождаются 2n дополнительных субгармоник на частотах
![]() ,
,
амплитуды, которых с ростом управляющего параметра l возрастают и к моменту следующей бифуркации становятся максимальными, подчиняясь универсальному соотношению
Амплитуды субгармоник появившихся в результате предшествующих n бифуркаций остаются неизменными.
Рис. 5. Изменение фурье-компонент в результате бифуркации (схематично)
В соответствии с вышеизложенным выражение для напряжения во вторичном контуре, в случае равенства первой гармоники частоты биений амплитуде напряжения воздействующего сигнала на резонансной частоте (UW = U2(w0)) и нулевой начальной фазе воздействующего сигнала (j0=0), с учетом первых трех гармоник частоты биений, определяется следующим образом:
в результате первой бифуркации
![]() ,
,
в результате второй бифуркации
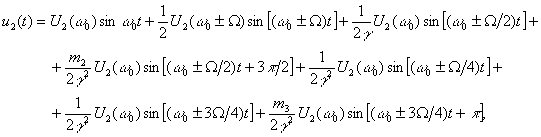
и т.д. Коэффициенты m2, m3 равны коэффициентам модуляции для второй и третьей гармоник частоты биений соответственно.
Формирование энергетического спектра системы в результате первых трех бифуркаций частоты биений с учетом амплитудно-частотной характеристики системы (1) и универсального соотношения (17) показано на рисунке 6. Коэффициент связи между контурами равен предельному значению. Начальные фазы трех гармоник частоты биений, как следует из выражения (6), равны соответственно 0, 3p/2 и p. Знаками (+) и (-) показаны сложение и вычитание появляющихся субгармоник в результате бифуркаций с различными начальными фазами.
Рис. 6. Спектр колебаний в связанных нелинейных колебательных контурах
для трех бифуркаций удвоения периода частоты биений
3. ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ полученных результатов
Механизм перехода к стохастичности через возникновение сложнопериодических колебаний в системе связанных нелинейных осцилляторов уверенно регистрируется и в физическом эксперименте. Измерения проводились в окрестности резонансной частоты осцилляторов, в качестве управляющего параметра использовались амплитуда и частота внешнего гармонического воздействия. Эволюция отображений Пуанкаре и спектров мощности колебаний в результате бифуркаций удвоения периода частоты биений показаны на рисунке 7.
Рис. 7. Эволюция отображений Пуанкаре и спектров мощности колебаний в результате бифуркаций удвоения периода частоты биений (физический эксперимент)
Из рисунка 7 видно, что при возникновении в системе амплитудной автомодуляции к спектру входного сигнала частоты w0 добавляются боковые составляющие w0 ± W, отвечающие режиму резонансных биений с частотой модуляции W (рис. 7, а). В спектре 2-тактных колебаний появляются гармоники половинной частоты w0 ± W/2, их амплитуды растут с увеличением глубины модуляции и достигают насыщения к моменту следующей бифуркации удвоения (рис. 7 б). В точке бифуркации появляются и плавно увеличиваются с ростом управляющего параметра компоненты спектра jW/4, j = 1,2, отвечая мягкому рождению цикла периода 4/jW (рис. 7 в). Тщательные измерения показали, что отношение интенсивности субгармоник jW/2n и jW/2n+1 для n = 0 и 1 составляет 10-12 дБ и достигает величины 13,0±0,3 дБ при n = 2. Данному отношению интенсивности субгармоник соответствует значение g » 0,045 при a » 2,5. В этом случае как видно из таблицы 1 показатель степени в выражении (10) р = 1 и система описывается квадратичным отображением.
В пределе накопления бифуркаций удвоения периода n>>1 становится справедливой масштабно инвариантная структура спектра в точках бифуркации. Дробление масштаба по оси частот соответствует делению интервала между ближайшими субгармониками пополам, а интенсивность возникших частотных компонент jW/2n+1 в точках бифуркации на 13 дБ меньше, чем интенсивность субгармоник jW/2n. При подходе к критической точке число предшествующих удвоений стремится к бесконечности и интервал частот между ближайшими субгармониками DWn ® 0. Спектр становится сплошным. Однако интенсивность субгармоник с ростом n очень резко убывает и стремится к нулю n ® ¥. С превышением порога стохастичности начинается процесс уширения спектральных линий высших субгармоник, приводящий к росту интенсивности сплошного шумового пьедестала в спектре. С некоторого значения параметра в эксперименте регистрируется сплошной спектр. Рисунок 7 г иллюстрирует спектр странного аттрактора при малом превышении над порогом, который соответствует размытому спектру 8-тактного цикла.
4. ВЫВОДЫ
Совокупность проведенных расчетов и представленных экспериментальных данных позволяет сделать вывод о возможности приближенного описания перехода к хаосу в системе связанных нелинейных осцилляторов при внешнем гармоническом воздействии через последовательность бифуркаций удвоения периода возникающей частоты биений между осцилляторами с помощью одномерного отображения типа квадратичной параболы и возникающей в системе амплитудной автомодуляции. Ширина энергетического спектра формируемого сигнала определяется амплитудно-частотной характеристикой системы связанных нелинейных осцилляторов.
1. Рюэль Д., Такенс Ф. О природе турбулентности // Странные аттракторы / Под. ред. Я.Г. Синая и Л.П. Шильникова.- М.: Мир, 1981. с. 117-151.
2. Шустер Г. Детерминированный хаос: Введение: Пер. с англ. - М.: Мир, 1998.
3. Афанасьев Б.П., Гольдин О.Е., Кляцкин И.Г. Теория линейных электрических цепей. - М.: Высшая школа, 1973.
4. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. - М.: Наука. Гл. ред. физ.-мат. лит., 1997.
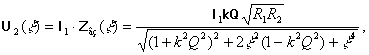 (1)
(1) . (6)
. (6)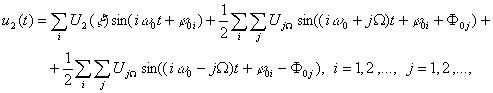 (8)
(8)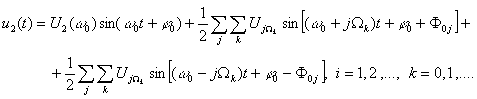 (12)
(12) ,
, 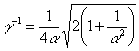 ,
(15)
,
(15)