|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2002 |
|
МЕТОД СТАТИСТИЧЕСКОГО ОБНАРУЖЕНИЯ НЕСАНКЦИОНИРОВАННЫХ ВТОРЖЕНИЙ В РАДИОКАНАЛ
И. М. Орощук, e-mail: Oroshchuk@yandex.ru
Тихоокеанский военно-морской институт им. С.О. Макарова, факультет радиосвязи.
Получена 25 мая 2003 г.
В статье представлен метод статистического обнаружения несанкционированных вторжений в цифровые радиоканалы в момент сеанса связи. Метод основан на оценке изменений математического ожидания процесса замираний по выборке значений амплитуд принимаемого сигнала. Кроме того, в работе представлена оценка эффективности данного метода, позволяющая определить оптимальные параметры сканирования для устройства, реализующего данный метод. Предлагаемый метод позволяет обеспечивать требуемую защиту радиосетей различного назначения от несанкционированных вторжений преднамеренного и непреднамеренного характера.
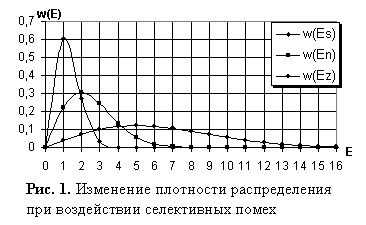
Проведенные теоретические исследования и практические эксперименты показывают, что при воздействии внешних селективных помех разного характера [1] в момент передачи полезных сообщений в цифровых каналах с регулярными замираниями происходят изменения стохастических характеристик принимаемого сигнала (рис. 1) [2-4]:
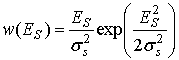 ;
;
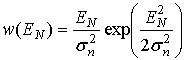 ;
;
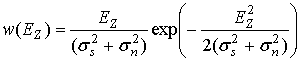 ,
,
где ![]() – амплитуда напряженности
поля полезного сигнала;
– амплитуда напряженности
поля полезного сигнала; ![]() – среднеквадратичное отклонение ортогональных
составляющих напряженности поля полезного сигнала;
– среднеквадратичное отклонение ортогональных
составляющих напряженности поля полезного сигнала; ![]() – амплитуда напряженности поля
селективной помехи;
– амплитуда напряженности поля
селективной помехи; ![]() –
среднеквадратичное отклонение ортогональных составляющих напряженности
поля селективной помехи;
–
среднеквадратичное отклонение ортогональных составляющих напряженности
поля селективной помехи; ![]() – амплитуда напряженности суммарного поля
полезного сигнала и селективной помехи. Данный факт позволяет осуществлять
обнаружение внешних воздействий нарушающих функционирование радиоканалов.
– амплитуда напряженности суммарного поля
полезного сигнала и селективной помехи. Данный факт позволяет осуществлять
обнаружение внешних воздействий нарушающих функционирование радиоканалов.
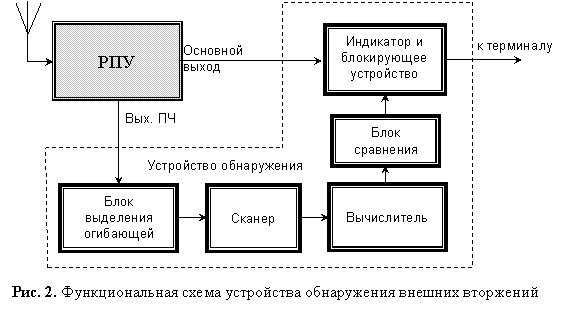
Сущность метода статистического обнаружения основана на обработке выборки данных принимаемого сигнала. Как показали исследования [2, 3], наиболее чувствительным является способ, основанный на оценке изменений статистики амплитуды. В качестве оценки предлагается использовать измерение математического ожидания (МО) стохастических флуктуаций амплитуды, вычисляемого как среднее арифметическое данных статистической выборки уровней принимаемого сигнала. На рис. 2 показана функциональная
схема устройства
реализации метода обнаружения несанкционированных вторжений в радиоканал.
Функционирование данной схемы заключается в выделении огибающей амплитуды
суммарного сигнала, поступающего с выхода тракта промежуточной частоты приемника.
После выделения огибающей выполняется сканирование амплитуды (снятие отсчетов).
Далее через установленный интервал выборки в вычислителе определяется среднее
арифметическое полученных значений амплитуд, которое сравнивается с пороговым
значением, зафиксированным в блоке сравнения в предшествующем периоде сканирования.
В случае если приращение среднего арифметического не превышает допустимое значение
[5], блок сравнения сохраняет полученное в вычислителе значение до очередного
периода сканирования. Если же изменение среднего арифметического амплитуды превышает
допустимое приращение, происходит срабатывание блока индикации и блокировки сигнала,
тем самым осуществляется оповещение оператора и исключение поступления к
терминалу сигнала внешнего вторжения. Следует заметить, что при обнаружении внешних
вторжений опасных для устойчивого приема полезной информации сигнал может
подвергаться специальной обработке, фильтрующей пораженный сигнал [6].
Для решения вопроса обнаружения возникает задача оценки изменений МО с определенной точностью и с заданной достоверностью, в противном случае задача лишается целесообразности. Согласно теореме Чебышева – Маркова [7] точность оценки МО независимых и зависимых случайных величин определяется, прежде всего, объемом выборки:
где
![]() – МО случайных
нормированных амплитуд сигнала (в дальнейшем амплитуд)
– МО случайных
нормированных амплитуд сигнала (в дальнейшем амплитуд) ![]() ;
; ![]() – дисперсия среднего арифметического
выборки случайных амплитуд;
– дисперсия среднего арифметического
выборки случайных амплитуд; 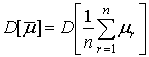 , e – сколь угодно малая величина, определяющая требуемую
точность оценки МО; n – объем выборки данных.
, e – сколь угодно малая величина, определяющая требуемую
точность оценки МО; n – объем выборки данных.
В общем случае при наличии корреляционной связи между значениями выборки случайной функции значение дисперсии среднего арифметического определяется выражением
где
![]() – дисперсия
случайной величины m;
– дисперсия
случайной величины m; ![]() – значение взаимной корреляции между двумя
случайными значениями выборки
– значение взаимной корреляции между двумя
случайными значениями выборки ![]() и
и ![]() .
.
Из
теоремы Маркова [7] известно, что значение ![]() должно снижаться по мере роста объема выборки.
Однако для практической оценки МО возникает определенная сложность, которая
заключается с одной стороны в ограниченности времени выборки из-за конечной
длительности самого сеанса связи, и с другой стороны большим интервалом
корреляции процесса замирания в реальных радиоканалах (рис. 3).
должно снижаться по мере роста объема выборки.
Однако для практической оценки МО возникает определенная сложность, которая
заключается с одной стороны в ограниченности времени выборки из-за конечной
длительности самого сеанса связи, и с другой стороны большим интервалом
корреляции процесса замирания в реальных радиоканалах (рис. 3).
В результате, для оптимизации выборки необходимо решать компромисс, обеспечивающий максимальную точность при минимальной длительности выборки в масштабе времени. Кроме того, в решаемой задаче стоит вопрос выбора оптимального интервала сканирования, который определяет объем выборки, и, следовательно, требуемые характеристики оперативной памяти устройства измерения. Из соображений целесообразности, длительность наблюдения должна быть минимальной, исходя из чего функцию автокорреляции (см. рис. 3) можно рассматривать на ограниченном интервале времени, на котором приближенно ее можно аппроксимировать экспонентой. Данному приближению адекватна математическая модель канала с замираниями и группированием ошибок, которая основана на учете влияния динамических изменений уровня сигнала [8].

Для оценки динамики замирания в предлагаемой
модели процесс изменений уровня сигнала разделен относительно медианного
значения ![]() на
два состояния, в результате чего можно выделит моменты замирания и усиления
сигнала (рис. 4). В момент замирания уровень сигнал ниже среднего, а в момент
усиления выше него.
на
два состояния, в результате чего можно выделит моменты замирания и усиления
сигнала (рис. 4). В момент замирания уровень сигнал ниже среднего, а в момент
усиления выше него.
Для упрощения модели с некоторым приближением на интервале замирания и усиления предлагается использовать средние значения коэффициента передачи эфира (см. рис. 4), величины которых для адекватности получим из известных значений числовых характеристик Рэлеевского распределения:
Из
решения системы уравнений (3) получим значения средних уровней на интервалах замирания
– ![]() и усиления
–
и усиления
– ![]() :
:
,
из которого
![]() ,
,
![]() .
.
На основании
полученных значений коэффициентов передачи можно определить соответствующие
вероятности ошибки приема бита (элемента) информации (![]() – на участке замирания сигнала,
– на участке замирания сигнала, ![]() – на участке усиления
сигнала) [8, 9].
– на участке усиления
сигнала) [8, 9].
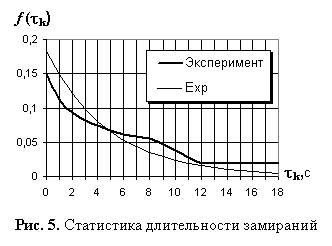
Анализ статистики замираний [10-11] показал, что длительности замирания и усиления распределены по экспоненциальному закону (рис. 5):
![]() ,
,
где
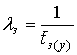 ,
, ![]() – средняя длительность
замирания или усиления сигнала.
– средняя длительность
замирания или усиления сигнала.
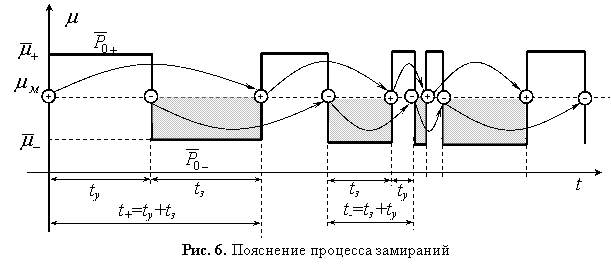
В результате, при экспоненциальном распределении длительности замираний моменты перехода канала в каждое состояние (замирания или усиления) представляют простейший пуассоновский поток [7]. Учитывая, что медианное значение уровня сигнала разделяет уровень на два равновероятных состояния, процесс перехода в одно из состояний представляет поток Эрланга второго порядка по отношению к общему потоку переходов в любое состояние (рис. 6).
В данном случае интенсивность переходов в определенное состояние (см. рис. 6) определяется выражением [7]
В
результате действия этих потоков канал переходит в одного из двух состояний: «З»
– замирания или «У» – усиления (рис. 7). При указанных потоках
данная система состояний канала описывается Марковской моделью [7].
Оба состояния канала составляют полную группу событий, в связи с чем
нормировочное условие будет определяться выражением ![]() .
.
Для определения вероятностей состояния модели составим уравнения Колмогорова:
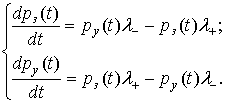
Из
решения системы полученных линейных дифференциальных уравнений с учетом нормировочного
условия и, в частности, при начальных условиях: ![]() определим соответствующие условные
вероятности состояний канала:
определим соответствующие условные
вероятности состояний канала:
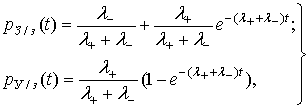
откуда с учетом формулы (4) получим:
и
по аналогии, при ![]() :
:
Исходя из полученных
выражений, можно определить значения состояний канала в стационарных условиях
при ![]() :
:
В данном случае сам
процесс замираний не имеет начальных условий (![]() ). Следовательно, надо полагать, что начало
сеанса связи всегда будет попадать на стационарный участок состояния канала.
Исходя из этого, вероятность попадания начала сеанса связи в то или иное
состояние будет определяться выражениями (7), откуда, соответственно, можно
записать вероятности начальных условий:
). Следовательно, надо полагать, что начало
сеанса связи всегда будет попадать на стационарный участок состояния канала.
Исходя из этого, вероятность попадания начала сеанса связи в то или иное
состояние будет определяться выражениями (7), откуда, соответственно, можно
записать вероятности начальных условий:
На основе полученных
выражений определим функцию автокорреляции процесса замирания в дискретные
интервалы времени (с интервалом квантования ![]() ):
):
где
![]() – возможные
значения коэффициентов передачи (в нашем случае
– возможные
значения коэффициентов передачи (в нашем случае ![]() или
или ![]() );
); ![]() – совместная вероятность состояний канала в
разные моменты времени.
– совместная вероятность состояний канала в
разные моменты времени.
Подставим соответствующие выражения данной модели в формулу (9):
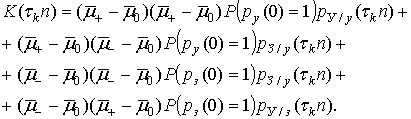
После ряда алгебраических преобразований с учетом формул (5), (6) и (8) получим:
Нормированная функция автокорреляции в данном случае будет определяться выражением
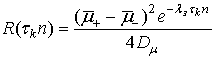 ,
,
где
![]() – дисперсия
коэффициента передачи эфира, значение которой с учетом формулы (3) будет равно
– дисперсия
коэффициента передачи эфира, значение которой с учетом формулы (3) будет равно
На основании полученного значения дисперсии [см. формулу (11)], нормированная функция автокорреляции будет определяться выражением
Для определения суммы
всех составляющих взаимной корреляции в выражении (2) проанализируем
корреляционную матрицу состояний канала через заданный интервал квантования ![]() . Данная матрица
образуется на основе значений взаимной корреляции между случайными величинами
(отсчетами значений амплитуд принятого сигнала):
. Данная матрица
образуется на основе значений взаимной корреляции между случайными величинами
(отсчетами значений амплитуд принятого сигнала):
где
![]() – коэффициенты
взаимной корреляции между случайными величинами
– коэффициенты
взаимной корреляции между случайными величинами![]() в разные моменты времени (
в разные моменты времени (![]() );
); ![]() – значения дисперсии случайных
величин.
– значения дисперсии случайных
величин.
Для дальнейших
расчетов определим значения МО ![]() и дисперсии
и дисперсии ![]() для каждого отсчета. Математическое
ожидание случайных величин
для каждого отсчета. Математическое
ожидание случайных величин ![]() определяется выражением
определяется выражением
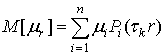 ,
,
где
![]() – значение
вероятности состояния канала через интервал времени
– значение
вероятности состояния канала через интервал времени ![]() , от начала сеанса связи.
, от начала сеанса связи.
Определим значение МО для представленной модели:
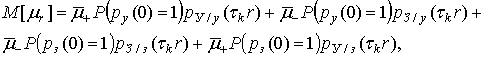
откуда с учетом формул (3), (5), (6) и (8) получим
Дисперсия случайных величин определяется выражением
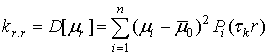 ,
,
величина которой для принятой модели будет равна
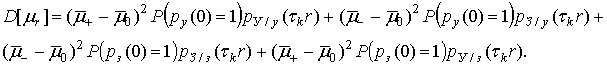
откуда также с учетом формул (3), (5), (6) и (8) получим
Из
выражений (14) и (15) видно, что МО и дисперсия случайной величины ![]() не зависят от времени
отсчета, что указывает на стационарность процесса замирания. Данный факт
подтверждает адекватность математической модели [10, 11].
не зависят от времени
отсчета, что указывает на стационарность процесса замирания. Данный факт
подтверждает адекватность математической модели [10, 11].
Величины ![]() (при
(при ![]() ) отличаются друг от
друга. На основании формулы (10) значения первой строки корреляционной матрицы
(13) вычисляются:
) отличаются друг от
друга. На основании формулы (10) значения первой строки корреляционной матрицы
(13) вычисляются:
В последующих строках значения изменятся, так как изменится совместная вероятность:
![]() .
.
С учетом формул (5), (6) и (8) совместную вероятность можно выразить:
![]() ,
,
в связи с чем выражение (16) преобразуется:
Сравнивая выражения (16) и (17), можно записать:
где
![]() – условная
вероятность i-го
состояния амплитуды канала через интервал
– условная
вероятность i-го
состояния амплитуды канала через интервал ![]() от начала отсчета, при условии, что в
начальных условиях он находился в том же состоянии – i;
от начала отсчета, при условии, что в
начальных условиях он находился в том же состоянии – i;
![]() – значение
взаимной корреляции между первым и последующими отсчетами (
– значение
взаимной корреляции между первым и последующими отсчетами (![]() ).
).
С учетом выражений (15) и (18), корреляционная матрица (13) примет вид
Откуда, с использованием формул (2), (16) и (17), значение дисперсии среднего арифметического выборки амплитуд сигнала можно определить выражением
Опуская громоздкие преобразования, запишем приближенное выражение для оценки дисперсии среднего арифметического выборки амплитуд сигнала:
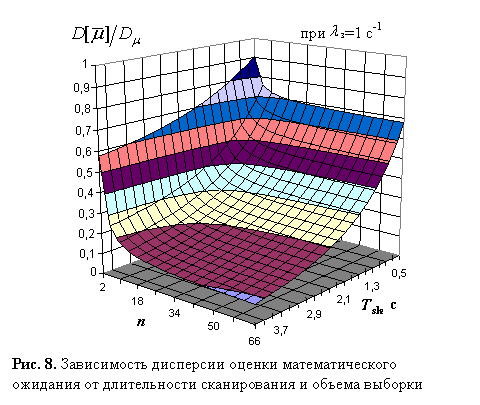
Для обнаружения несанкционированных вторжений в
радиоканалы систем связи, использующих кратковременные сеансы связи, актуально
рассмотреть зависимость дисперсии оценки МО от объема выборки при различных
интервалах сканирования – ![]() , которая представлена на рис. 8.
, которая представлена на рис. 8.
В
результате, согласно полученным графикам (см. рис. 8), в зависимости от поставленных
ограничений, можно определить необходимый объем выборки для достижения
требуемой дисперсии оценки МО при заданном интервале сканирования либо, зафиксировав
объем выборки, определить требуемый интервал сканирования. Требуемая дисперсия
оценки МО вычисляется по формуле (1), из которой при заданной точности e и
достоверности метода измерения 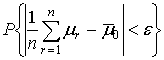 определяется максимальное значение
дисперсии оценки МО:
определяется максимальное значение
дисперсии оценки МО:
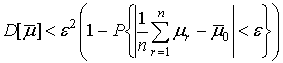 .
.
В дальнейшем, пользуясь выражением (21) либо графиками функции дисперсии (см. рис. 8), определяются параметры устройства статистического обнаружения воздействия несанкционированных вторжений в радиоканал.
Литература.
1. Oroshchuk I.M. New technologies of unauthorized influence on automatic radio communication systems. Tomsk, TUSUR 18.05.1999 // The 3-rd international symposium "Sibconvers’99”, 1999. V-2. – pp. 336-338. (на английском).
2. Oroshchuk I. The statistical detection method of unauthorized intrusions in the Rayleigh fading channel. St. Petersburg 26.05.2002 // 1st IEEE International Conference on Circuits and Systems for Communications. Proceedings. 2002. – pp. 424-427. (на английском).
- Орощук И.М. Статистические изменения в радиоканале с регулярными замираниями при воздействии имитопомех. Пенза, ПГУ май 2002 // Научно-техническая конференция: "Безопасность информационных технологий", Сборник докладов, 2002. - Том 3. Секция 6. – С. 76-80.
- Орощук И.М. Метод обнаружения и фильтрации имитационных помех в Рэлеевских каналах с замираниями // Безопасность информационных технологий: Москва, МИФИ. – № 3. – 2002. – С. 75-79.
- Орощук И.М., Аксенов В.П. Технологические особенности применения десинхронизирующих имитопомех в автоматизированных системах связи. Санкт-Петербург 11.06.2001 // Международная конференция по телекоммуникациям (IEEE/ICC2001/St. Petersburg). 2001. – 4 с. //http://www.eltech.ru/icc2001spb/rus /Program.htm
- Oroshchuk I.M. The filtering method of the digital radio channels by the frequency shift keying from the imitohindrances. Moscow, Russia 12.03.2003 // 5th International Conference «Digital signal processing and its applications». 2003. – 4 pp. (на английском).
- Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Наука, 1991. – 384 с.
- Орощук И.М. Динамическая модель Рэлеевского канала с замираниями // Журнал радиоэлектроники: М.: № 10. - 2002. – 10 с.
http://www.jre.cplire.ru/jre/oct02/index.html
10. Долуханов М.П. Флуктуационные процессы при распространении радиоволн. М.: Связь, 1971. – 184 с.
11. Головин О.В. Декаметровая радиосвязь. М.: Радио и связь, 1990. – 240 с.
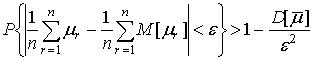 , (1)
, (1)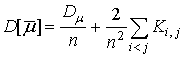 , (2)
, (2)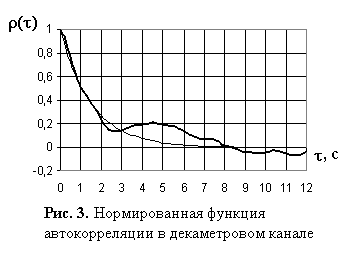
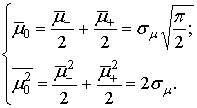 (3)
(3)
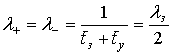 .
(4)
.
(4)
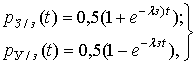 (5)
(5)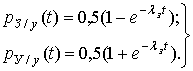 (6)
(6)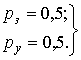 (7)
(7)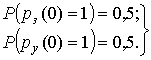 (8)
(8)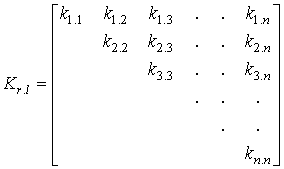
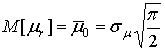 .
(14)
.
(14)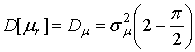 .
(15)
.
(15)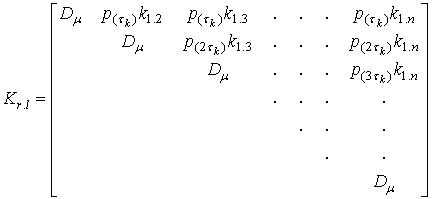
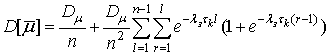 . (20)
. (20)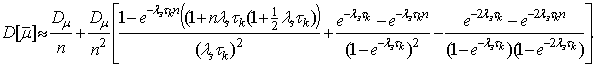 (21)
(21)