"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 5, 2007

оглавление

дискуссия

УДК  519.72 + 539.12

Пороговые информационные ограничения,  вносимые приемником в тракт передачи сигналов

С. Г. Басиладзе
НИИ Ядерной Физики МГУ

Постановка задачи

 

В обобщенной форме аналоговый сигнал может быть представлен непрерывной математической функцией y=F(x). Сигнал может быть описан и с использованием спектральной гармонической переменной: c=1/x. Переменной ‘x’ может быть как время, так и пространственная координата, а переменной c - частота или волновое число, соответственно. Квадрат функции времени: y=F(t), определяет приращение энергии сигнала на интервале dt (или интервале df), т.е. с одной стороны
 

dE = y²*dt,      с другой      dE = (g²/2)*df,                 (1,а,б)
 

где g(f) - спектральная плотность амплитуды сигнала (коэффициент 1/2  при g² вытекает из синусоидальной формы гармоник).

Классический одиночный сигнал имеет непрерывный спектр; хотя последний спадает достаточно резко в области высших гармоник, тем не менее, g(f) не обращается в нуль ни на одном конечном df  вплоть до бесконечности.

Согласно Винеру [1], количество информации, получаемое в результате нахождения (с точностью dy) положения точки на интервале Y, ограничено сверху величиной:
 

I £ log(Y/dy);                                                              (2)
 

здесь отношение Y/dy есть число доступных обнаружению (различимых) состояний положения точки. В определении Винера по умолчанию полагается, что каждая “порция” информации приобретается в результате некоторого события (например, акта измерения). Если говорить о сигнале, то акт получения от него очередной порции информации, согласно теореме отсчетов [2¸5], носящей в отечественной литературе имя Котельникова, происходит на “единичном” интервале – dt, задаваемом шириной спектра сигнала – Df: dt=1/2Df.

Если Y неограниченно возрастает, либо dy неограниченно уменьшается, то количество получаемой информации стремится к бесконечности, чего не должно быть в принципе (информация, как логарифм вероятности, конечна по определению). Следовательно, для значений Y должен существовать некоторый предел, а значение dy, в свою очередь, не может быть меньше некоторой пороговой величины.

В триаде: передатчик – передающая среда – приемник, каждое звено по-своему вносит ограничения на пропускную способность тракта передачи в целом. Со стороны передатчика очевидным предельным ограничением является мощность, отдаваемая в канал передачи. Именно мощность – P играет роль предела в известной формуле Шеннона [5] для плотности потока передаваемой информации:
 

DI/Dt = Df * log[1 + (P / <P_N>)].                             (3,а)
 

Ограничителем снизу на число различимых состояний в (3,а) является средняя мощность шума <P_N>, неизбежно присутствующая в тракте передачи (индекс N от ‘noise’). Поскольку мощность есть квадрат огибающей сигнала, то эту формулу при большом числе состояний можно представить в виде:
 

DI/Dt = Df * log[1 + (Y/dy)²] » 2Df * log(Y/dy) = log(Y/dy) / dt.      (3,б)
 

В результате, в числителе дроби справа имеем количество информации по Винеру (2), а в знаменателе – единичную длину по Котельникову, что подтверждает высказанные выше соображения.

Широкая распространенность формулы Шеннона порождает у многих иллюзию того, что шум является единственным или, по крайней мере, всегда является основным фактором количественного ограничения dy снизу.

Характеристическая энергия теплового шума, как известно [6],  равна 4kT (k – постоянная Больцмана, T – абсолютная температура); для комнатной температуры это 1,6*10^-20 Дж. Если, например, паразитная емкость на входе приемника C_П»1 пФ, а уровень различимости сигнала составляет U_П»1 мВ (типовая величина, для приемников сигналов с кабельных линий связи), тогда требуемая входная энергия заведомо больше C_П*U_П²/2=5*10^-19 Дж. Как видим, это в десятки раз выше уровня теплового шума, не считая того, что последний  может быть уменьшен в сотни раз понижением температуры входа приемника. Приведем еще несколько примеров, где шумы практически отсутствуют, не ограничиваясь рамками существующих технических приложений.

Наиболее наглядной является газовая акустическая среда: мы не воспринимаем шума хаотического движения молекул в газе, однако прекрасно слышим упорядоченные звуки, распространяющиеся по среде, образованной случайными столкновениями молекул. Реально имеющийся порог слышимости (не будь его, не было бы децибелов) не имеет прямого отношения к уровню шума передающей среды и тем более к наличию шума в ушах.

Сходная ситуация имеется и с электроном на атомной орбите, который хаотически “дрожит” под действием “нулевых колебаний” вакуума, в результате чего появляется лэмбовский сдвиг [7] спектральных линий. Однако, этот шум не размывает орбитальных уровней энергии, и состояний орбитального движения электрона; последние могут быть использованы в “компьютерах квантовой механики” (выражение Фейнмана [8]).

Следует упомянуть и о пространственных сигналах, где шум практически отсутствует, но информация, тем не менее, теряется за счет обрезания спектра волновых чисел. Например, если информация передается в виде текста на экран через проектор, то при расфокусировке объектива проектора текст на экране станет нечитаемым. Обрезание спектра частот динамического сигнала, по сути, и есть его “расфокусировка” во времени.

Наконец шум, поскольку он не имеет постоянной составляющей, не является принципиальным ограничением для приема информации; скорее, он ограничивает темп ее приема. Влияние шума можно низвести теоретически до нуля, если производить его усреднение путем многократного повторения сигналов. Например, вся квантовая механика есть наука о средних величинах, где экспериментальная информация получается длительным “набором статистики”, т.е. усреднением шумов (неопределенностей) микромира.

Смысл того, что мы будем называть информационным порогом, состоит в том, что подпороговыми сигналами вообще нельзя передать информацию. В качестве пороговой величины при получении, например, экспериментальной информации может выступать систематическая погрешность измерений.

В сказанном нет ничего удивительного, ибо каждому интуитивно понятно, что распознавание состояний сигнала может зависеть не только от наличия шума, но и от такого понятия как чувствительность приемника. Наивно было бы полагать, что “зона нечувствительности” может быть бесконечно малой или всегда меньшей, чем шум.

Настоящая работа была предпринята с целью проведения по возможности полного анализа вида, границ существования и количественных характеристик информационных ограничений, вносимых приемником. Ставилась задача выявить принципиальные, общие ограничения, не зависящие от конкретной технической реализации приемника. Ясно, что такая задача может быть решена лишь на основе анализа самых общих физических закономерностей восприятия сигналов. Полученные в работе выражения органично включают в себя и классический шум, а также порог по действию в макро- и микромире.

 

О чувствительности приемника

 

Нетрудно декларировать наличие у приемника порога чувствительности, сложнее понять, в чем именно заключается его физический механизм. К счастью, возможных вариантов не так уж много, ограничителем снизу может быть:

1) значение огибающей сигнала (или амплитуда короткого импульса);

2) значение мощности, точнее энергия на единичном интервале по ‘t’;

3) ширина спектра сигналов во времени или в пространстве – Dc=1/dx;

4) ограничения по ширине спектра и по энергии могут действовать совместно.

К первому определению прямо подталкивает формула Винера (2). Порог по амплитуде обычно подразумевает нелинейность входной характеристики приемника. Мы будем рассматривать ниже только линейные приемники; тогда, как будет показано ниже, невозможность регистрации сигналов малой амплитуды есть следствие наличия порогов 2)¸4) и пункт 1) можно исключить из списка причин. Энерго-ограничение 2) является очевидным, поскольку невозможно изменить состояние приемника, не передав ему никакой энергии. Фундаментальность ограничения 3), связанного с ограниченностью градиента сигнала: Y/dx, также не нуждается в особых пояснениях; во времени оно отражает универсальное свойство инерции, а в пространстве – ограниченность силы. Ограничение 4) является порогом по действию [9], оно также является всеобщим, поскольку принцип наименьшего действия является одним из основных законов природы.

 

 

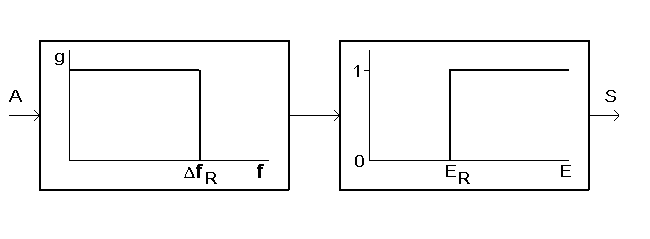
Рис.1. Обобщенная функциональная схема логического регистратора отклонений сигнала: A - аналоговый вход, S - логический выход;

            первое звено - фильтр гармоник  f>f_R, второе звено - дискриминатор по энергии на уровне E_R.   

    Величины  Df_R и E_R  определяют пороговую постоянную регистратора: H_R = E_R / 2Df_R, которая равна квадрату спектральной плотности

    амплитуды нулевой гармоники - g₀²  порогового входного сигнала или     квадрату его площади.

 

 

Обобщенная функциональная схема приемника. Следуя традициям электронной техники можно представить ограничения 2) и 3) в виде отдельных функциональных узлов приемника (хотя можно ввести и соответствующие математически операторы). Тогда функция 4) отобразится последовательным соединением узлов 3) и 2), т.е. произведением некоммутируемых операторов “быстроты” и энергии. В результате получим достаточно простую и наглядную обобщенную блок-схему, показанную на рис.1. Ее функциями обеспечивается различимость состояний сигнала, а на уровне порога – сам факт регистрации.

Если подать на такой регистратор низкочастотный сигнал (например, импульс с очень пологим фронтом) то момент срабатывания регистратора будет соответствовать достижению энергии входного сигнала пороговой величины, т.е. пункту 2).

Если же подать “быстро-медленный” испытательный сигнал в виде ступеньки малой амплитуды, то задержка его срабатывания также будет достаточно велика, поскольку на накопление необходимой второму узлу энергии (после фильтрации “быстрой” части энергии, например, паразитной емкостью в первом узле) потребуется значительное время. При токе входного сигнала 1 нА и для взятого во введении численного примера (C_П=1 пФ, E_П=5*10^-19 Дж), это произойдет не ранее, чем через 1 мкс. Этот случай соответствует пункту 3), регистратор будет обнаруживать ступеньку сколь угодно малой амплитуды, т.е. для этого типа сигнала его порог по амплитуде равен нулю.

Пункт 4) реализуется, если в качестве испытательного взять “быстрый” сигнал (например, прямоугольный импульс длительностью 10 нс). Тогда у регистратора появится порог по амплитуде (не менее 100 нА); он будет тем больше, чем уже входной сигнал. При увеличении амплитуды сигнала задержка срабатывания будет уменьшаться, сначала быстро, а затем все медленней стремясь к нулю. Этот “эффект гуляния” (walking) электронных дискриминаторов, вносящий аппаратную погрешность как в измерение времени, так и амплитуды, хорошо известен в наносекундной технике [10].

 

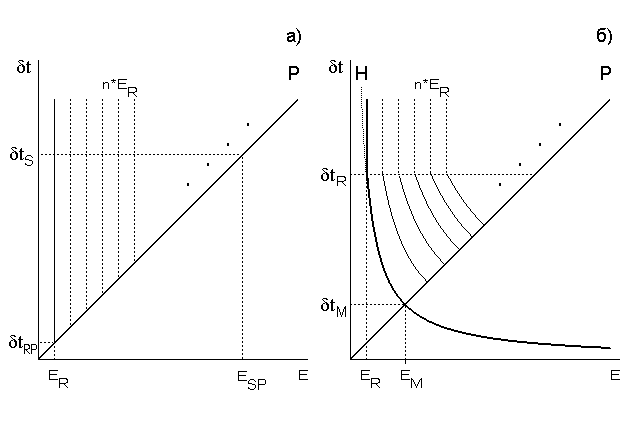
Рис.2. Информационные ограничения при практическом отсутствии шумов задаются сверху пределом мощности сигнала - P, а снизу зависят от

    быстродействия приемника:
a) если приемник “быстрый” (dt_R << dt_S), то он воспринимает  n=E_SP/E_R состояний в сигнале (плюс ‘0’),  при увеличении быстроты сигнала количество различимых состояний снижается, но темп передачи информации растет (снижении dt_S действует сильнее) и достигает максимума при   dt_S = dt_RP = E_R/P;

    б) если приемник “медленный” (dt_R > dt_S > dt_M), то ограничение снизу идет по пороговым гиперболам и число различимых состояний

         снижается,  кроме того, приемник воспринимает информацию с темпом, определяемым  dt_R, а не входным сигналом.

 

Таким образом, приведенная на рис.1 обобщенная функциональная схема, покрывает все возможные физические варианты ограничений при приеме сигналов (включая первый в списке, как следствие). Оценим, задавшись единичным интервалом времени dt=1нс, порог по действию 4): H_П=dt*E_П=5*10^-28 Дж*с; как видим, он на 6 десятичных порядков выше постоянной Планка. В численных примерах, использованных выше, мы в разных формах обыгрывали комбинацию: P=1 нВт, dt=1 нс, которая ориентировочно соответствует уровню восприятия сигналов массовой продукцией современной электронной техники.

Перейдем теперь к выводу общих формул, описывающих те или иные варианты информационных ограничений. Для большей наглядности мы будем иллюстрировать их графиками на плоскости параметров [E,dt] – “энергия-быстродействие”. Ограничение мощности передатчика задается на этой плоскости прямой линией, проходящей через начало координат.

 

Пороговые ограничения при регистрации сигналов

 

Рассмотрим возможные режимы работы регистратора, которые, как мы выяснили, определяются соотношением между быстротой сигнала (S) и быстродействием самого регистратора (R).

“Быстрый” регистратор. Повторим, что если сигнал имеет значительно меньшую ширину спектра, чем у приемника: dt_S>>dt_R (или Df_S<<Df_R), то он не фильтруется и целиком проходит во второе звено. В этом случае срабатывание регистратора определяется текущей величиной энергии сигнала и наступает сразу же, как только последняя становится больше E_R.

Тогда на плоскости параметров [E_R,dt_R] различаемые приемником состояния есть вертикальные линии, идущие с шагом E_R вплоть до предельной прямой – P (см. рис.2,а). Для сигнала с быстродействием dt_S, количество таких состояний: n=E_SP/E_R, где E_SP=P*dt_S. Соответственно, возможная плотность передачи информации во времени:
 

 DI_S / dt = log[1 + (P*dt_S / E_R)] / dt_S,                        (4,а)
 

здесь дополнительная единица появляется, как и в формуле Шеннона (3,а), из учета “состояния отсутствия” сигнала.

Информационный приоритет отсчетов над состояниями. Как видно из (4,а), при уменьшении dt_S, несмотря на то, что количество различимых состояний снижается, возможная плотность передаваемой информации, тем не менее, возрастает (поскольку логарифм меняется медленнее, чем 1/dt_S). Наибольшая плотность информации будет достигнута при повышении быстроты сигнала (интенсивности отсчетов), т.е. снижении dt_S до величины  dt_RP=E_R/P, где различаются  только 2 состояния:
 

(DI_S / dt)_MAX = log[2]*P / E_R.                                  (4,б)
 

Если сигнал сопоставим по ширине спектра с приемником, то на плоскости параметров [E_R,dt_R] зона, где регистратор является "быстрым", а сигнал "медленным" лежит выше горизонтальной прямой, проходящей через точку  dt_R  на оси ординат - рис.2,б (штриховая линия).

“Медленный” регистратор. Если же сигнал имеет большую ширину спектра, чем приемник (выходит за пределы основной полосы частот последнего): dt_S<dt_R (или Df_S>Df_R), то только часть энергии сигнала, содержащаяся в его нижних гармониках, пройдет во второе звено (рис.1):
 

E_REG = (g_LOW² / 2) * Df_R,                                           (5,а)
 

здесь g_LOW - спектральная плотность амплитуды сигнала в области низших гармоник. Для реальных сигналов спектральная плотность амплитуды в области самых нижних гармоник практически постоянна, поэтому (5,а) эквивалентно условию
 

E_REG = g₀² * 2Df_R,                                                    (5,б)
 

где g₀=g_LOW/2 – спектральная плотность амплитуды нулевой гармоники.

По мере роста Df_S все большая и большая часть энергии сигнала будет отфильтрована, т.е. потеряна для регистрации. Как следствие, все больше и больше информации, содержащейся в коротких деталях сигнала, будет утеряно.

Пороговое соотношение неопределимости. Для регистрации короткого сигнала “воспринимаемая” энергия E_REG должна быть больше или равна E_R. Это можно записать в виде неравенства, вытекающего из (5,б):
 

g₀² ³ E_R / 2Df_R,                                                        (6,а)
 

Это значит, что для коротких (для него) сигналов приемник имеет пороговую информационную постоянную
 

H_R = E_R / Df_R = E_R * dt_R                                         (6,б)
 

с размерностью действия.

Для сигнала величина  g₀²  есть квадрат его площади [11]; она также (6,а) имеет размерность действия, в данном случае это действие сигнала: g₀²=H_S. Тогда пороговое условие принимает весьма простой вид:
 

H_S ³ H_R.                                                                 (6,в)
 

Соответственно, область сигналов, регистрируемых медленным приемником, на рис.2,б будет располагаться справа от (пороговой) гиперболы, проходящей через точку [E_R,dt_R], поскольку  E_S»g₀²*Df_S=H_S/dt_S.

Легко также видеть из рис.2,б, что условие (6,в) справедливо и для быстрого регистратора, поскольку вертикальная прямая E_R=const проходит справа от пороговой гиперболы - H. Таким образом, условие (6,в) задает обобщенный порог приемника (точнее, является его необходимым условием).

Интервал обнаружения порогового сигнала. Как видим, короткие (для приемника) сигналы все же могут быть зарегистрированы за счет роста их площади (квадрат площади сигнала - H_S должен быть больше H_R - квадрата "пороговой площади" [12]). Однако, медленный регистратор срабатывает не в интервале наличия сигнала, а заведомо позже - по прошествии интервала:
 

dt_R = H_R / E_R = 1 / 2Df_R,                                             (7)
 

требуемого для "набора пороговой площади". Для чувствительных, но медленных регистраторов интервал обнаружения может быть достаточно большим. Хорошим примером является “регистрация“ вспышки молнии глазом – сама вспышка длится доли микросекунды (но она очень яркая), а глаз воспринимает ее через десятки миллисекунд.

Биполярные короткие сигналы. Входной сигнал в интервале, меньшем dt_R, интегрируется приемником (поскольку величина 1/dt_R находится выше границы спектральной полосы приемника). Если в интервале, меньшем dt_R, появится несколько входных сигналов, то для регистратора они будут суммироваться не по амплитудам огибающих, а по площадям.

Представим, что имеется короткий биполярный сигнал или два коротких одинаковых сигнала противоположной полярности, отстоящих на расстояние, существенно меньшее dt_R. В подобной паре оба сигнала не будут зарегистрированы, даже если они надпороговые (каждый имеет большую площадь), ибо их суммарная площадь в интервале обнаружения нулевая.

Количество “пороговых” состояний. Предположим, что сигнал несет только подпороговые "детали", тогда они, как и сам сигнал, будут потеряны при регистрации. Точно также не будут восприняты детали, лежащие между гиперболами H и 2H на рис.2 (хотя сам сигнал уже будет воспринят) потому, что невозможно определить разность между пороговым сигналом и сигналом, лежащим ниже гиперболы 2H. Следующий "слой" неразличимости лежит в границах от 2H до 3H и так далее.

Следовательно, линии  n*H  (n - целое число) задают информационные состояния сигнала (начиная с порогового) и только они являются различимыми. На рис.2,б ограничиваемая пороговой и предельной асимптотами область, где реальный сигнал удовлетворяет информационным ограничениям, заполнена линиями (гиперболы), идущими с шагом H.

Информационная пропускная способность. На пороговой гиперболе сигнал имеет только 2 состояния (он есть или его нет). Это значит, что на каждом интервале dt он может нести 1 бит информации, а на интервале L*dt - L бит (независимо от того сколько раз он появился - один или L-раз).

При движении вправо по горизонтали от точки [E_R,dt_R] до предельной прямой количество возможных состояний сигнала, как нетрудно убедиться, равно n=(dt_R/dt_M)²,  где dt_M=ÖH/P есть ордината точки пересечения пороговой гиперболы и предельной прямой на рис.2,б.

Если сигнал становится быстрее (dt_S<dt_R), то количество состояний снижается до n=dt_S*dt_R/dt_M², соответственно, возможная плотность информации во времени принимает вид:
 

 DI_R / dt = log[1 + (dt_S*dt_R / dt_M²)] / dt_R.                     (8)
 

В отличие от (4,а), значение dt в знаменателе (8) равно dt_R (потому, что на регистрацию сигнала тратится интервал dt_R). При уменьшении dt_S величина под знаком логарифма снижается, а знаменатель в (8) неизменен,  в результате, информационная способность тракта передачи уменьшается. Этот эффект делает энергетически невыгодным использование “слишком быстрых” сигналов в технике, поэтому описанный режим передачи информации до сих пор не привлекал особого внимания в теории сигналов. Однако, практически он используется  весьма  широко – достаточно  упомянуть  кино и телевидение: в каждой точке экрана сигнал в каждом кадре очень короткий, намного меньший, чем  dt_R  зрительного канала человека.

 

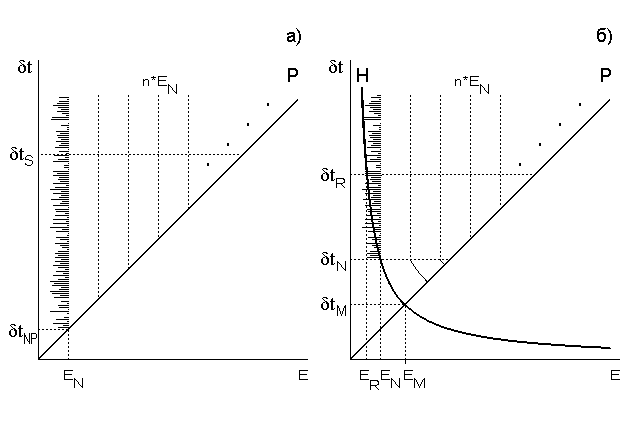
Рис.3. Информационные ограничения при подавляющем влиянии шумов задаются сверху пределом мощности сигнала - P, а снизу зависят от

    E_N  шума и  H  приемника:

            а) при пренебрежимо малых  E_R  и  dt_R  (весьма малом H) количество регистрируемых состояний определяется формулой Шеннона (11),

         а темп передачи информации зависит только от быстроты сигнала  - dt_S  (вплоть до  dt_S=dt_NP);

    б) если же приемник медленный, но чувствительный  (dt_R > dt_S,  но E_R < E_N),  то шум действует вплоть до уровня порога - dt_N,  а далее

         положение и количество регистрируемых состояний определяется гиперболами, идущими с шагом  H=E_R*dt_R.

    Ниже горизонтали  dt_N  рост быстродействия сопряжен с возрастанием энергозатрат на передачу одного бита информации.

 

  

Информационные ограничения, создаваемые шумом

 

Все известные физические носители сигналов обладают определенным уровнем шума, т.е. содержат некоторую неупорядоченную фоновую энергию.

Для электрических сигналов имеется два основных вида шумов: тепловой, средняя мощность которого [6]:
 

<P> = 4kT*Df_N,                                                      (9,а)
 

где  Df_N - полоса частот шума;

а также дробовой шум, порождаемый дискретностью носителей заряда, со средней мощностью [13]:
 

<P> = 2e*DU*Df_N,                                                 (9,б)
 

где     e - заряд электрона,

       DU - проходимая носителями разность потенциалов.

В обоих случаях параметром шума является некоторая величина энергии - E_N; для теплового шума это 4kT, а для дробового - 2e*DU. Из (9) ясно, что E_N это средняя энергия шумовой линии на "быстротном" интервале  dt_N=1/2Df_N.

При комнатной температуре характеристическая энергия дробового шума превосходит энергию теплового шума при DU>50 мВ. Поэтому при генерации сигналов основной вклад дает дробовой шум, а при их приеме - тепловой.

Быстрый чувствительный регистратор. При постоянных условиях (T=const, DU=const) энергия E_N=const - постоянна, поэтому в обоих случаях на плоскости [E, dt] линия шума есть вертикальная прямая – рис.3,а (так же, как при приеме медленных сигналов - рис.2,а). На этой прямой средняя мощность <P_N> и среднее действие <H_N> не являются константами и определяются из уравнений, аналогичных (9,а,б):
 

<P_N> / Df_N =  E_N  = <H_N> * Df_N.                         (10,а,б)
 

С учетом (10,а), для быстрого регистратора достаточно высокой чувствительности, по аналогии с (4,а) получаем формулу Шеннона (3,а):
 

DI_N / dt = log(1 + (P / <P_N>)) / dt_S.                       (11,а)
 

Это вполне логично, поскольку именно размытость шумовой линии задает здесь ширину интервалов между вертикальными линиями состояний - n*E_N. При увеличении быстроты сигнала возможная плотность передачи информации возрастает и наибольшая плотность будет достигнута, если dt_S снизить до величины  dt_NP=E_N/P, где различаются  только 2 состояния:
 

(DI_N / dt)_MAX = log[2]*P / E_N.                               (11,б)
 

Медленный чувствительный регистратор. Если  dt_S<dt_R (или Df_S>Df_R),  и  E_R<E_N,  то как видно из рис.3,б, картина в целом повторяет показанную на рис.2,б. Выше горизонтали dt_N линии состояний идут вертикально, а ниже – переходят в гиперболы, идущие с шагом H=E_R*dt_R. Заметим, что и на рис.2,б, темп (частота) распознавания сигналов определяется величиной dt_R, т.е. может быть низкой по сравнению с возможной частотой входных сигналов – 2/dt_S.

 

 

 

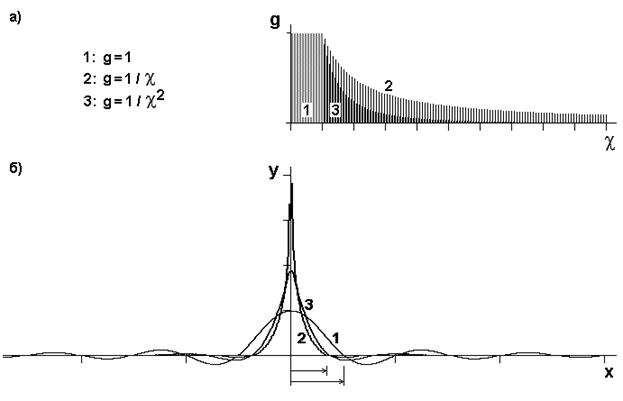
Рис.4. Типы сигналов (в пространстве или времени):

 а) 1 - плоский, обрезанный спектр функции отсчетов;

   1,2 - спектр классического сигнала, спадающий по закону ~1/c,

   1,3 - спектр классического сигнала, спадающий по закону ~1/c² за пределами основной полосы;

   гармониками являются косинусоиды (с нулевой фазой);

 б) 1 - функция отсчетов, вида sin(x)/x  (имеет плоский спектр ‘1’);

   2 - сигнал со спектром ~1/c;

   3 - сигнал со спектром ~1/c².

Период пересечения нулевой линии у функции отсчетов на 25¸30% больше, чем у сигналов с бесконечным спектром (помечено стрелками); сигналы 2 и 3 по расстоянию между опорными точками различаются незначительно.

 

 

Граница классического шума. Пороговая постоянная приемника H зависит от его физических размеров: чем они меньше, тем она ниже. При переходе к “нанотехнологиям” неизбежно появится природное физическое ограничение на уменьшение величины H в виде постоянной Планка – h.

Как видно из рис.3,б, граница обрезания классического шума проходит по пороговой гиперболе, заменив ‘H’ на ‘h” получаем ограничение на полосу частот классического шума:
 

2Df_N = E_N / h.                                                        (12,а)
 

Для теплового шума  E_N=4kT  (9,а), тогда  условие обрезания можно записать в следующем виде:
 

HDf_N / kT = 2.                                                       (12,б)
 

Именно отношение  hDf_N / kT  входит, как обрезающий параметр, в известную формулу Планка [14] для нахождения верхней границы спектра теплового излучения (шума) в полости.

Для температуры T=300^oK граница обрезания классического теплового шума находится на уровне: Df_N=1,3*10¹³ Гц. Этот диапазон частот всего на 2-3 десятичных порядка выше освоенного современной техникой передачи сигналов, поэтому он представляется достижимым в недалеком будущем.  При T=300^oK на границе обрезания энергозатраты на передачу информации составляют 1,6*10^-20 Дж/бит, а мощность на входе приемника находится на уровне 4,2*10^-7 Вт. Однако, ниже указанной границы (ниже dt_N на рис.3,б) энергия, затрачиваемая на каждый бит передаваемой информации, в силу появления порога по действию, должна существенно возрастать.

 

Информация за пределами основной полосы спектра

 

До сих пор мы интересовались количеством информации, которая воспринимается приемником из основной полосы частот сигнала – Df_m (на рис.4,а – спектр 1). В соответствии с теоремой отсчетов “основная полоса” по умолчанию имеет строго ограниченный (обрезанный) спектр такой же, как у функции отсчетов. Подобный спектр динамического сигнала легко вводится в математике, однако, физически он не реализуем, т.к. нарушает условие причинности [1]. Из соображения конечности энергии квадрат спектральной плотности амплитуды – g²(f) за пределами основной полосы должен спадать не слабее, чем по закону 1/f² (на рис.4,а – спектры 2 или 3). Это значит, что там может находиться до половины энергии сигнала; странно было бы думать, что эта энергия не способна нести информацию.

Не претендуя на полноту анализа, сделаем простые численные оценки. Построим огибающие сигналов, имеющих спектры 1¸3; это выполнено на рис.4,б. Как видим, период повторения нулевых значений у функции отсчетов (т.е. расстояние - dx  между опорными точками) на 25¸30% больше, чем у сигналов  с  бесконечным  спектром;  это характеризует  разницу  в возможном темпе приема информации. Следовательно, полученные нами (и Шенноном) формулы являются достаточно приближенными (хотя и хорошо отражают смысл происходящих явлений). Более того, поскольку спектр за пределами основной полосы может иметь бесконечное разнообразие форм, то у рассматриваемой задачи не существует общего точного решения.

 

 

 

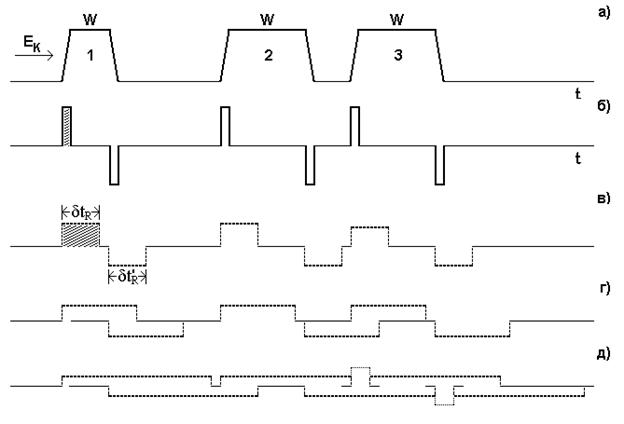
Рис.5. Взаимодействие частицы с потенциальным барьером – а)  может быть   представлено в терминах теории сигналов, как считывание частицей

   на фронте и срезе барьера  - б)  значений перепадов его энергии.

Если время регистрации dt_R (14,а) меньше, чем протяженность барьера,  то частица затормозится – в); если же оно больше dt_R (перекрываются пороговые “интервалы различимости“  dt_R  и dt^’_R  от фронта и среза барьера), как для сигнала 1 – г), или для сигналов 1 и 2 – д), то частица пройдет сквозь барьер (туннельный эффект).

   Если же перекрываются интервалы различимости  dt_R  от фронтов соседних барьеров, что возможно при короткой паузе между барьерами

   2 и 3 – д), то порогом будет их суммарная площадь;  в результате, второй и третий барьеры совместно могут оказаться непроницаемыми,

   хотя сами по себе он проницаемы.

   Интервал различимости, порожденный инертностью, эквивалентен пороговому сигналу (на фрагменте  в)  выделен штриховкой),    вызывающему отражение частицы; его энергия всегда равна энергии штрихованного сигнала на фрагменте б);  это значит, что при переходе

   от  б)  к  в), а также при переходах от  б)  к  г), или от  б)  к  д),  сигнал эволюционирует как квадратичная дельта-функция.

 

 

Регистрация микросигналов

 

Хотя это не входит прямо в задачу данной работы, остановимся кратко на регистрации сигналов в микромире, поскольку именно в нем в наиболее отчетливой форме проявляются пороговые ограничения по действию (ниже – просто порог). Рассмотрим случай когда “приемником” является частица, а сигналом – потенциальный барьер, с которым она взаимодействует.

Квадратичная дельта-функция как сигнал. Обычная дельта-функция Дирака есть короткий сигнал, в процессе роста амплитуды и “обужения” которого сохраняется постоянной площадь и, как следствие, величина его действия. Поэтому дельта-функция Дирака может быть как надпороговой (большая площадь), так и подпороговой (малая площадь).

Представим себе теперь, что процесс роста амплитуды и обужения идет при сохранении неизменной площади квадрата огибающей, т.е. энергии импульсного сигнала. Этот процесс соответствует на рис.2 движению вертикально вниз из-за чего спектральная плотность амплитуды сигнала – g(f) постоянно снижается (тогда как у дельта-функции Дирака она постоянна), что неизбежно приводит к тому, что квадратичная дельта-функция становится подпороговой.

Классический шум представляет из себя совокупность случайно распределенных во времени квадратичных дельта-функций, именно поэтому он фильтруется по пороговому ограничению.

Очевидно, что обратный процесс “размазывания” квадратичной дельта-функции, соответствующий движению вертикально вверх на рис.2, сопряжен ростом ее действия, в результате чего она становится надпороговой.

Потенциальный барьер как сигнал. Рассмотрим простейший случай, когда  потенциальный барьер имеет квази-ступенчатую форму, т.е. весьма короткие перепады – рис.5,а. Эти перепады образуются двумя сигналами, близкими к дельта-функциям – положительной (образует фронт) и отрицательной (образует срез барьера) – рис.5,б.

Будем считать, что на барьер двигается частица с кинетической энергией E_к, меньшей чем W, т.е. в классической механике она должна остановиться и отразиться от фронта барьера. В микромире этого не происходит, ибо получаемый частицей “сигнал торможения” является подпороговым (при очень коротком фронте барьера его действие меньше ‘h’ – постоянной Планка). Физический мир устроен так, что действие накапливается (интегрируется) при движении, поэтому через некоторое время – dt_R оно (как квадратичная дельта-функция) неизбежно достигнет порогового уровня (рис.5,в - слева). Тогда, если задержка на регистрацию фронта барьера dt_R окажется больше, чем продолжительность барьера (рис.5,г, слева), то частица пройдет барьер насквозь (туннельный эффект) потому, что сигналы от перепадов потенциала разнополярные и их суммарная площадь в интервале dt_R нулевая (см. раздел “Биполярные короткие сигналы”). Приведенное описание несколько упрощено, т.к. в действительности эта картина заметно размыта микрошумами.

Сказанное можно выразить в виде порогового соотношения:
 

/E_к – W/ * dt_R  ³  h                                             (14,а)
 

здесь разность E_к–W есть функция Лагранжа [15], интеграл от которой по времени определяет действие (в рассматриваемом случае E_к–W@const). Численную величину dt_R можно сопоставить с полосой частот регистрации (рис.1):  dt_R=1/2Df_R. Для сравнения приведем еще раз полученное выше необходимое условие регистрации классического сигнала H_S³H_R в следующем виде:
 

E_S * dt_S  ³  H_R.                                        (14,б)
 

Как видим, оба эти условия, хотя и несколько отличаются по форме, по смыслу они являются пороговыми соотношениями неопределимости и в их правой части фигурирует порог при приеме сигналов.

Разница в виде формул (14,а) и (14,б) следует из различий физических механизмов восприятия микро и макро-сигналов. Если для макро-приемника существует понятие длительности входного сигнала, высокочастотная часть энергии которого фильтруется “медленным” приемником, то в микромире энергия всегда воспринимается целиком, но происходит это с некоторой задержкой. Сигнал здесь представляет из себя “размазываемую” во времени (до уровня dt_R)  квадратичную дельта-функцию, как это наглядно видно из рис.5,б¸в (выделено косой штриховкой).

Время восприятия микро-сигналов определяется значением dt непосредственно на пороговой гиперболе – рис.2,б и при большой энергии оно может быть достаточно малым. Напомним, что для макро-приемника dt_R всегда соответствует точке стыка порога по энергии и по действию (8), т.е. лежит в самом начале пороговой гиперболы.

 

Заключение

 

Все разнообразные электронные устройства, включая аналоговые схемы, создаются, в конечном счете, для восприятия информации на своем входе. Исходными для информации являются понятия события и состояния (лишь затем появляется вероятность тех или иных состояний в событиях). Для аналогового сигнала проблема выделения событий в первом приближении решается теоремой отсчетов (дискретизацией времени). Проблема выделения различимых состояний, начиная с Шеннона и по сию пору, анализируется только как задача “обрезания шума” (по амплитуде). При таком подходе погрешности в сигнале, которые искажают принятую информацию, рассматриваются как отклонения от значений сигнала в отдельно взятой точке. Подобные рассуждения не совсем приемлемы при анализе сигналов потому, что значение сигнала не тождественно состоянию сигнала. Приемник физически не способен выделять состояния ни из точечных, ни из средних значений сигнала, поскольку он является анализатором энергии сигнала в конечном интервале времени (в конечной полосе частот). Именно этот физический механизм ответственен за появление информационных состояний сигнала, т.е. за его квантование.

Только для идеального приемника (неограниченного быстродействия и весьма высокой чувствительности по энергии) единственным ограничителем снизу является средняя мощность шума - <P_N> или, что тоже, его характеристическая энергия E_N в полосе частот сигнала. Тогда возможная плотность передаваемой информации определяется соотношением (10,б). Если быстрота приемника или входного сигнала ниже, чем отношение (средней) шумовой энергии E_N к пределу мощности P, то информационная пропускная способность заметно ниже и определяется формулой Шеннона (11,а).

При пренебрежимо малом уровне шума и быстром приемнике ограничителем снизу является его энергочувствительность - E_R (4,б). Если приемник медленный, то появляется дополнительное ограничение, задаваемой величиной dt_R. Информационная пропускная способность в этом случае определяется формулой (4,а), сходной с формулой Шеннона, где вместо средней шумовой мощности стоит отношение  E_R/dt_R.

Наконец, последним, возможным вариантом приема сигналов является такой, когда и чувствительность и быстродействие совместно ограничивают информационную пропускную способность тракта передачи сигналов. В этом случае порогом является уровень минимального действия приемника: H_R=E_R*dt_R. Пороговое ограничение одинаково влияет на прием, как при наличии шума, так и при его отсутствии (поскольку шум в этой зоне интегрируется приемником). Шумовые ограничения являются более “мягкими” по сравнению с пороговыми. Если имеется возможность повторной передачи (повторного измерения), то информацию можно извлечь из под шума; из под порога этого сделать в принципе невозможно.

Имеется естественное, природное ограничение на диапазон частот классического теплового шума, поскольку порог регистрации не может быть меньше, чем постоянная Планка. В области микро-масштабов проявляются пороговые эффекты квантовой механики, порог по действию здесь играет главную роль в задании шага между различимыми состояниями. Количество же состояний над уровнем естественного порога определяется пределом мощности электромагнитного взаимодействия. 

 

Литература

 

1. Н.Винер. Кибернетика. М.: Наука, 1983.

 

2. E.T.Whittaker, Proc.Roy.Soc., Edinburg, V35, 1915, p.181-184.

 

3. R.V.L.Hartley, Bell Sys.Tech.J.,7,3, 1928, p.535-563.

 

4. В.А.Котельников, О пропускной способности "эфира" и проволоки в электросвязи, Материалы к 1-му Всесоюзному съезду по вопросам      реконструкции дела связи и развития слаботочной промышленности. Изд-во "Ред.связи РККА", 1933.

 

5. C.E.Shannon, A mathematical theory of communications, Bell Syst. Tech. Journal, 1948, 27, P.379-423.

 

6. H.Nyquist, Thermal agitation of electric charge in conductors,  Phys.Rev., 1928, V.32 No 1. P.110-113.

 

7. Физика микромира, Маленькая энциклопедия п/р Д.В.Ширкова. М.: Советская энциклопедия 1980.

 

8. R.Feinman. Quantum Mechanical Computers, Plenary Talk presented to IQEC-CLEO Meeting, Anaheim, June 16, 1984.

 

9. С.Г.Басиладзе, Пороговые и предельные соотношения для сигналов, Препринт НИИЯФ МГУ 2004-20/759, Москва 2004 г.

 

10. С.Г.Басиладзе. Быстродействующая ядерная электроника. М.: Энергоиздат, 1982 г.

 

11. И.С.Гоноровский. Радиотехнические цепи и сигналы.  М.: Радио и Связь, 1986.
 

12. С.Г.Басиладзе, Сигнал, данные и информация в физических измерениях,  Физика Элементарных Частиц и Атомного Ядра, 2000, том 31, вып.3.

 

13. A.Qilespi. Signal, noise and resolution in nuclear counter amplifiers. Pergamon press, 1953.

 

14. М.Планк. Теория теплового излучения. М. 1935.

 

15. Р.Фейнман, Р.Лейтон, М.Сэндс. Фейнмановские лекции по физике, Т.6. М.: Мир, 1966.