удк 62-506
синтез конструкции и закона юстировки
управляемой составной поверхностью параболоида главного рефлектора большого радиотелескопа
М. В. Белов
Санкт-Петербургский государственный политехнический университет
Получена 4 мая 2011 г.
Аннотация. Описаны основные конструктивные схемы управляемой составной многопанельной отражающей поверхности главного зеркала большого полноповоротного радиотелескопа миллиметрового диапазона с каркасно-ферменным основанием, использующей при сборке зеркальные щиты гексагональной или трапецеидальной форм, как статически определенного жесткого тела с управляемой пространственной поверхностной фигурой. Выявлены необходимые и достаточные условия геометрической неизменяемости составной поверхности. Сформированы структурные свойства многоэлементной поверхностной структуры и установлены условия ее управляемости. Предложен итерационный закон юстировочного позиционирования пространственного положения реперных точек составной зеркальной поверхности, асимптотически устойчивый в окрестности поверхности стабилизации.
Ключевые слова: радиотелескоп, главный рефлектор, составная отражающая поверхность, геометрическая неизменяемость, реперные точки, неуправляемые и управляемые связи, управляемость, юстировка, асимптотическая устойчивость.
Abstract. It is described general structural schemes of the composite controlled multipanel reflecting surface of the large millimeter radio telescope’s main reflector with frame-truss bottom, which uses hexagonal or trapezoidal mirror shields as statically defined rigid body with controlled spatial surface. Necessary and sufficient terms of the geometric invariability of the composite surface are identified. Also structural properties of the multielement surface structure and terms of its controllability are formed. The iterative asymptotically stable in vicinity of stabilization’s surface principle of adjusting positioning of spatial location of the reflecting surface’s fixed points is proposed.
Key worlds: radio telescope, main reflector, composite reflecting surface, geometrical invariability, fixed points, controlled and uncontrolled ties, controllability, adjustment, asymptotic stability.
1. Введение
Освоение в радиоастрономии миллиметрового диапазона длин волн привело к тому, что заметно возросли требования к качеству параболической поверхности рефлектора антенны, стабильности взаимного расположения главного зеркала и контррефлектора. Вместе с тем многотонный вес, температурные изменения приводят к деформациям элементов конструкции радиотелескопа, к нарастающим линейным смещениям точек поверхности главного зеркала. По этим причинам для достижения требуемых точностных параметров аппроксимации параболоида вращения главного рефлектора многоэлементной составной зеркальной поверхностью используются специальные средства адаптации отражающей поверхности и автоматической подстройки положения контррефлектора, оснащенные электромеханической системой коррекции возникающих деформаций и возмущений.
Подобные многоэлементные зеркальные конструкции обычно называются активными составными отражающими поверхностями [1] и они относятся к классу статически определимых регулярных или псевдорегулярных структур, представляя собой пространственные объекты, образованные однотипными (или ограниченным числом типоразмеров) многократно повторяющимися элементами, связанными между собой или с несущей конструкцией однотипным образом. Такие статически определимые многоэлементные структуры занимают промежуточное положение между механизмами и статически неопределимыми системами и позволяют осуществлять сборку и управление формой большой многоэлементной конструкции без напряжений и не требуют при этом организации согласованной работы множества исполнительных механизмов.
Естественно важными вопросами при этом являются определение базовых конструкций многоэлементной отражающей поверхности, способов сборки составных пространственных структур и настройки такого исходного (доэксплуатационного) пространственного положения их зеркальных щитов, при котором обеспечивается заданная точность аппроксимации составной поверхностью некоторого эталонного параболоида вращения.
2. Базовые пространственные конструкции многоэлементных
отражающих поверхностей с каркасно-ферменным основанием
Пусть имеются две панели (фацеты,
пластины, зеркальных элемента, щита – все эти понятия в рассматриваемом
контексте статьи являются синонимами), между которыми имеются определенное
число связей, и они закреплены на некотором несущем каркасе. Тогда, при общем
количестве связей 
одной
панели с соседними компонентами (с соседней панелью и несущим каркасом)
выбранным из условия 
,
такая система представляет собой механизм,
при 
– имеет
место статически определимая,
а при 
– статически неопределимая конструкция.
Статически определимая конструкция, занимая промежуточное положение между
механизмами и статически неопределимыми конструкциями, обладает важными для
высокоточных составных поверхностей свойствами:
1. Ошибки в изготовлении (настройке) связей не приводят к деформации составных зеркальных поверхностей при их сборке.
2. Освобождение произвольной связи превращает конструкцию в механизм с одной степенью свободы. Размещая в освобожденной связи прецизионный исполнительный механизм, можно тем самым управлять формой составной поверхности, трансформируя ее пространственную структуру за счет изменения взаимного положения зеркальных щитов без упругих деформаций.
Заметим,
что отмеченные свойства распространяются и на составную многоэлементную
конструкцию, содержащую 
панелей. Для последней необходимое условие статической определимости
записывается следующим образом:
.
(1) Выбирая число связей для
каждой из панелей из условия (1) и
распределяя их по многоэлементной составной структуре различным образом, можно
получить различные типы управляемых отражающих поверхностей.
Вопросы управления формой многоэлементной составной поверхности являются, пожалуй, самыми важными, прежде всего, с точки зрения достижения требуемой точности соблюдения формы поверхностной структуры для обеспечения заданной частотной эффективности функционирования радиоастрономических инструментов или систем космической связи. В сложившейся традиции для подобных структур задача управления формой больших составных конструкций обычно рассматривается как квазистатическая и носит кинематический характер. Тогда многопанельная составная структура является управляемой, если при произвольных малых нарушениях связей, вызванных тепловыми и ветровыми воздействиями, гравитационными возмущениями, неточностями изготовления, сборки и юстировки, деформациями и другими причинами, существуют такие положения регулируемых связей, при которых все управляемые панели занимают требуемое положение, восстанавливая при этом заданную погрешность аппроксимации идеальной отражающей поверхности многоэлементной составной пространственной конструкцией и компенсируя тем самым негативное влияние возмущающих факторов.
Возникает естественный вопрос – сколько связей между отражающими панелями, между панелями и несущим каркасом радиоантенны делать регулируемыми, если общее число связей в многоэлементной составной конструкции выбирается из условия (1)? Здесь необходимо учитывать тот факт, что поверхности, предназначенные для отражения электромагнитных волн, делятся на два больших класса:
1. Составные
зеркальные поверхности, обеспечивающие заданное направление отражения излучения
от каждой панели
(направление нормали к поверхности панели). Для этого случая необходимым
условием управляемости является выбор количества 
управляемых связей на основании следующего
неравенства:
. (2)2. Составные антенные конструкции, обеспечивающие заданную фазу отражения сигнала. Для обеспечения этого режима отражения на каждую панели необходимо вывести три реперных точки на стабилизируемую поверхность и необходимое условие управляемости при этом записывается как:
Другим важным вопросом является определение базовой конструкции многоэлементной отражающей поверхности. Анализируя конструктивные решения, используемые при построении антенных систем наземных радиотелескопов миллиметрового диапазона и центров космической связи [1-5], в качестве базовой конструкции составного многозеркального рефлектора большого радиотелескопа выделим составную многоэлементную отражающую поверхностную структуру с каркасно-ферменным основанием. Пример подобных конструкций отражающих поверхностей представлен на рис. 1. Для обеспечения статической определимости данной конструкции зеркальной поверхности каждая из отражающих пластин-фацет имеет шесть кинематических связей с соседними элементами, при этом три кинематических связи реализуются с каркасно-ферменным основанием, при этом именно эти связи выполняются регулируемыми.
Рис. 1. Многопанельное главное зеркало радиотелескопа:
а) Геометрическая модель с каркасно-ферменным основанием;
b) Пространственная модель с опорно-поворотным устройством;
с) Пространственная модель ферменного каркаса.
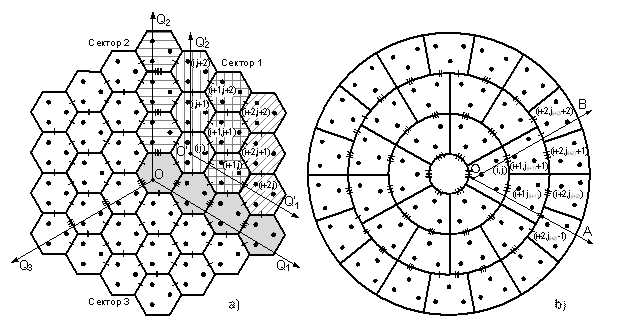
В конструктивном плане отражающие поверхности с каркасно-ферменным основанием могут быть реализованы с использованием зеркальных панелей различных форм. В практике создания зеркальных систем главных рефлекторов современных наземных радиотелескопов миллиметрового диапазона нашли применение две основные базовые пространственные структуры многоэлементных отражающих поверхностей: конструкции с использованием однотипных гексагональных (шестиугольных) панелей (рис. 2.a) и конструкции на основе трапецеидальных разнотипных щитов (рис. 2.b).
Рис. 2 Базовые схемы построения составной отражающей поверхности:
a) На основе гексагональных панелей;
b) На основе трапецеидальных панелей разных типоразмеров.
Установим порядок наращивания числа панелей в представленных на рис. 2 схемах и минимальный состав нерегулируемых межэлементных связей, необходимый для организации первичной сборки составной поверхности зеркала.
Введем на рис. 2.a двухиндексную нумерацию отражающих
панелей так, чтобы индексы 
и 
при 
, 
соответствовали бы панелям,
располагающимся на опорных направлениях, которых в схеме с гексагональными
зеркалами можно выделить три – располагаемые по осям OQ1, OQ2, OQ3. Учитывая эффект тройственности
симметрии гексагональной схемы, позволяющей в ней выделить три идентичных
сектора (сектора 1,2,3) ограничимся только анализом только одно сектора,
например, сектора 1. При сборке поверхности сначала соединяются панели
находящиеся на одном из опорных направлений, например, на оси OX, в последовательности: 
; затем производится
присоединение отражающих панелей рядами в следующем порядке: 
;…; 
. При этом следует учесть, что
центральная панель с индексом 
жестко закреплена на несущем ферменном каркасе
и этот каркас также задействуется для организации кинематических связей с
устанавливаемыми панелями. При присоединении любых панелей к ранее
установленным фрагментам сектора необходимо учитывать базовое требование, заключающееся
в том, что каждая устанавливаемая
панель должна иметь шесть кинематических связей с элементами конструкции
формируемой составной поверхности и с ферменным каркасом в совокупности, причем
три из этих связей согласно соотношениям (3) должны быть регулируемыми. Тогда
присоединение каждой панели на опорном направлении (в рассматриваемом секторе 1
это направление оси OQ1) приводит к необходимости введения
трех нерегулируемых связей с уже закрепленной панелью и трех регулируемых
связей с ферменным каркасом, причем точки присоединения последних (по три на
каждую пластину) смещены на 50% от вершины к центру пластины [4] (на рис. 2.a эти точки обозначены черными кружками внутри каждой
шестиугольной фигуры панели). По завершении сборки исходного опорного
направления (ось OQ1) добавление следующих панелей,
осуществляемое по рядам, приводит к необходимости подключения первой панели ряда
с индексом как
опорной, т.е. с введением трех неуправляемых связей с ранее установленной
опорной панелью 
в
предыдущем ряду и трех управляемых по принятой системе для собираемой составной
поверхности. Это связано с тем, что все панели с индексами вида находятся на втором
опорном направлении, т.е. на оси OQ2.
Другие панели, добавляемые в неопорные ряды, присоединяются к уже установленным
панелям, с которыми граничат своими ребрами, одиночными неуправляемыми связями,
т.е. крепятся к панелям с индексами 
, 
, 
, а три оставшиеся связи таких панелей
делаются регулируемыми и они организуются с ферменным каркасом. В конечном
итоге схема организации неуправляемых связей гексагональных панелей принимает
вид, условно показанный на рис. 2.a, где число связей между панелями и их конкретное расположение отображено
числом «перечеркиваний» граничащих ребер панелей. Точки присоединения
регулируемых связей на любой панели неопорных направлений располагаются также
как и на панелях опорных направления.
На рис. 2.b используется несколько иная система
двухиндексной нумерации панелей. В индексе 
позиция 
соответствует номеру слоя, а позиция 
– номеру отражающей
панели в слое, при этом, как и в предыдущем случае, центральная панель с
индексом жестко
закреплена на ферменном каркасе основания отражающей поверхности. Каждая
панель 
-го слоя
связана с панелями -го
слоя тремя неуправляемыми связями, остальные три связи этих панелей делаются
регулируемыми и они формируются с ферменным основанием составной поверхности.
Связи между соседними панелями в пределах -го слоя отсутствуют. Это позволяет
наращивать поверхность слоями, начиная от центрального сегмента . При установлении
панелей -го
слоя в случаях, когда добавляемая панель контактирует одновременно с двумя
панелями 
-го
слоя, общее количество неуправляемых связей с ними также остается равным трем,
однако они распределяются так, чтобы со всеми контактируемыми щитами -го слоя существовали
связи. Количество отражающих сегментов в последовательных слоях либо одинаково,
либо удваивается, с тем, чтобы радиальные края панелей лежали бы вдоль общих
радиальных линий, насколько это возможно. Это позволяет свести к минимуму
ситуации, когда панель следующего -го слоя контактирует с двумя разными
пластинами предыдущего -го слоя. Точки присоединения регулируемых
связей к пластинам (по три на каждую) смещены на 50% от вершины к центру пластин
[4]. На рис.2.b эти точки присоединения условно показаны в виде черных
кружков внутри трапецеидальных фигур пластин. Таким образом, каждая пластина -го слоя всегда связана
с панелями -го
слоя тремя неуправляемыми связями, а остальные три кинематические вязи пластины
реализуются с ферменным основанием и они выполняются регулируемыми.
3. Условия геометрической неизменяемости составной
отражающей поверхности
Произвольное размещение связей в конструкциях многоэлементных отражающих поверхностей не гарантирует геометрическую неизменяемость таких пространственных структур, поскольку равенство (1) является лишь необходимым условием их статической определимости. Для геометрической неизменяемости требуется обеспечить невырожденность (независимость) этих связей. Установим эти условия геометрической неизменяемости.
Каждую отражающую панель статически определимой конструкции, собранной по любой из приведенных на рис. 2 схем сборки, можно рассматривать как твердое тело, произвольное перемещение которого складывается из поступательного движения и вращения.
Введем локальную
систему координат 
,
связанную с -й
отражающей панелью и зададим пространственное положение этой панели вектором 
. Здесь первые три
компоненты вектора 
, т.е. вектор 
, определяют начало
(точку 
локальной
системы координат в неподвижной системе координат 
, связанной с центром сегмента
, а вращение
задается вектором 
,
направленным по оси вращения -ой панели и равным по
длине углу поворота.
Аналогично вектором 
зададим
на ферменном каркасе основания составной отражающей поверхности
пространственное положение области опорных точек регулируемых связей -ой
панели (при этом 
,
).
Тогда произвольная 
-я 
связь на опорных направлениях
схемы сборки по рис. 2.a (для
сектора 1) между соседними панелями может быть задана как:
и 
, 
, (4)
если связь является нерегулируемой; и
и 
, 
, (5)
если связь регулируемая.
Вся система связей пластин на опорных направлениях есть:
, 
. (6)
Пластины с индексами ,
находящимися не на опорных направлениях, согласно рассмотренной в пп. 2
процедуре наращивания присоединяются одиночными неуправляемыми связями к
панелям с индексами ,
, и тремя регулируемыми
связями к соответствующей -й области основания,
предназначенной для организации опорных точек регулируемых связей -ой
панели. Следовательно, уравнения связей этих соединений -ой неопорной панели имеют вид
,
(7)где 
, 
, 
; 
Положим, что при 
, удовлетворяющем
условиям (6), (7), выполнено неравенство:
.
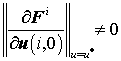(8)
Тогда, в силу справедливости
теоремы о неявных функциях в окрестности состояния 
, первое уравнение системы (6) разрешимо относительно 
и на опорном направлении
по оси OQ1 пространственное положение 
-й панели однозначно определяется
положением 
-й
пластины и положением -й
области основания, предназначенной для организации опорных
точек регулируемых связей -ой панели.
Отсюда следует, что крепление -й панели опорного направления OQ1 геометрически неизменяемо, т.е. является
жестким.
Выполнение условий
.
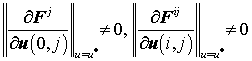(9)
гарантирует геометрически неизменяемое (жесткое) наращивание зеркальных панелей на опорном направлении OQ2 и остальных направлениях сборки 1-го сектора схемы составной отражающей поверхности, приведенной на рис. 2.a. Заметим, что аналогично записываются условия геометрической неизменяемости и для остальных секторов (сектора 2 и сектора 3) отражающей поверхности, собранной их гексагональных зеркальных щитов. .
При
использовании для построения отражающей поверхности трапецеидальных пластин (рис.
2.b) процесс наращивания
отражающей поверхности осуществляется послойно, при этом опорных направлений
сборки нет, вследствие чего система уравнений связей строится для каждой -й панели с учетом числа
панелей -го слоя, с которыми
контактирует эта панель, и количества связей с этими панелями -го слоя, а также с
учетом связей с -й областью основания. В общем виде эта система уравнений связи совпадает с
системой (7), в которой локальные уравнения регулируемых связей есть 
, где индексом 
обозначен номер панели
на -м слое, а
вид описаний связей 
зависит
от конкретного местоположения -й панели на составной
поверхности отражателя. Так, например, для схемы сборки поверхности,
приведенной на рис. 2.b, для панелей первого слоя (
, 
) уравнения локальных связей имеют следующий вид: 
; для 2-го слоя, при 
,
, 
)
– вид 
или
; для третьего
слоя (, 
, 
) – 
для связей панелей с номерами 
и 
либо 
для связи щитов с индексами 
и 
для
связей вида 
.
Если положить, что для схемы сборки
конструкции отражающей поверхности из трапецеидальных панелей для каждой -й
пластины выполняется второе из условий (9), т.е.
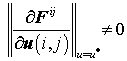(10)
и удовлетворяет условию (7) для схемы сборки
поверхности по рис. 2.b, то для каждой -й
пластины гарантируется геометрически неизменяемое (жесткое) наращивание панелей
в порядке, описанном в пп. 3, при этом пространственное положение -й
панели на -м
слое однозначно определяется положением сопряженного отражающего щита на -м
слое (или положением двух щитов -го слоя, если
имеет место постоянное соединение с ними) и положением -й области каркасно-фермененого основания, предназначенной для
организации опорных точек регулируемых связей -ой отражающей панели.
Рассуждения и описания кинематических ограничений и связей до сих велись в приложении к математическим уравнениям связей. Однако на практике реализации одной физической связи может приводить к нескольким кинематическим ограничениям и нескольким уравнениям связей. Например, стержень, защемленный с одной стороны и закрепленный на другой стороне с помощью сферического шарнира, описывается тремя уравнениями связей.
Рассмотрим простейший случай, когда каждая физическая связь, как нерегулируемая, так и регулируемая в конструкции отражающей поверхности из трапецеидальных панелей реализована посредством стержня, закрепленного с обеих сторон с помощью сферических шарниров. Такое соединение приводит к одному кинематическому ограничению и одному уравнению связей. Покажем, что в конструкции подобной составной поверхности, собранной, например, по схеме рис. 2.b, размещение точек крепления связей согласно рис. 3 обеспечивает выполнение условия (10).
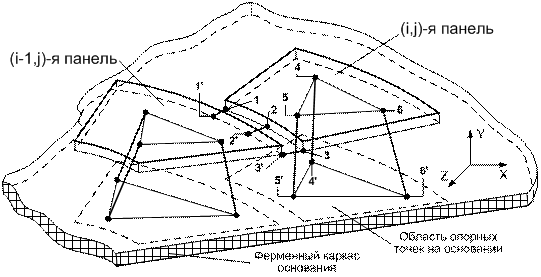
Рис. 3. Схема размещения связей между элементами конструкции
отражающей поверхности, собранной из трапецеидальных пластин:
неуправляемых между панелями (связи 1,2,3) и
регулируемых между панелями и основанием (связи 4,5,6).
Точки 
, расположенные на -й присоединяемой
пластине, в рассмотренной процедуре наращивания, назовем входными точками крепления -й панели. Выходные точки крепления 
соединительных
стержней находятся на -й
панели ранее собранной части конструкции -го
слоя отражающей поверхности и в -й области расположения опорных
точек регулируемых связей на основании поверхности.
Зададим
пространственное положение каждой входной и выходной точек крепления каждой из связей -й панели в абсолютной
(неподвижной) и
локальной системе
координат в виде следующих векторов:
1. Вектор положения -й входной точки
крепления в неподвижной системе координат 
.
2. Вектор положения 
-й 
выходной точки
крепления в неподвижной системе координат 
.
3. Вектор направления и
длины -й соединительного
стержня невозмущенной конструкции 
.
4. Вектор положения -й входной точки
крепления в локальной системе координат 
.
Запишем уравнение связи -й связи -й
панели в виде
(11)
и продифференцируем его, учитывая, что
, (12)
где вектор 
определяет сдвиг -й
панели, а матрица 
, 
определяет ее поворот.
После завершения вычислений получаем:
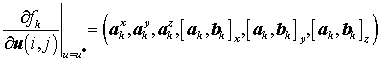, (13)
где 
– 
-я, 
, компонента векторного
произведения.
Отсюда следует, что условие
(10) геометрической неизменности положения -й панели необходимо
переписать в виде
.
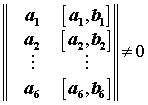(14)
Выполнение
неравенств (14) для всех -х панелей есть достаточное условие геометрической
неизменяемости в схеме сборки отражающей поверхности, представленной
на рис. 2.b.
4. Характеризация структурных свойств составной отражающей поверхности как объекта регулирования
Как объект управления конструкции многоэлементных зеркальных поверхностей (рис. 2) должны обладать следующими структурными свойствами:
Свойство 1. При фиксированном положении управляемых связей конструкции являются геометрически неизменяемыми, т.е. ведут себя как твердое тело (обладают шестью степенями свободы), если элементы конструкций и связи ведут себя как жесткие тела.
Свойство 2. Сборка конструкций и регулирование их форм не приводят к упругим деформациям панелей.
Свойство 3. Часть связей управляема и снабжена исполнительными механизмами для изменения пространственного положения элементов конструкций.
Свойство 4. Конструкции допускают наращивание, при этом присоединение нового элемента происходит с минимальной перестройкой ранее подключенных связей. Добавление одного элемента сопровождаться перестройкой связей лишь между небольшим числом (обычно не более чем тремя) ранее закрепленных в конструкции панелей, к которым вновь присоединяемая пластина крепится.
Свойство 5. Любая из рассмотренных конструкций представляет собой управляемый объект регулирования, т.к. при фиксации в требуемом положении на поверхности стабилизации реперных точек одной из панелей и произвольных малых неточностях изготовления, сборки, остаточных, термических, ветровых и иных деформациях существует такое положение управляемых связей, при котором все остальные реперные точки других отражающих щитов лежат на стабилизируемой поверхности.
Покажем, что любая из упомянутых конструкций многоэлементных поверхностей с каркасно-ферменным основанием (рис. 2), использующая схемы управления формой, ведет себя как статически определенное жесткое тело с управляемой пространственной поверхностной фигурой и тем самым удовлетворяет свойствам 1…5. Для этого докажем утверждение.
Утверждение 1. Пусть заданы:
– число панелей,
образующих составную конструкцию;
– число нерегулируемых связей
панелей с соседними элементами конструкции;
– число управляемых связей с
основанием составной конструкции;
– число реперных точек на составной поверхности (по 3 на каждой панели).
Тогда составные конструкции поверхностей с актуаторными схемами управления их формой удовлетворяют свойствам 1…5, если выполняются следующие условия:
,
(15)
,
(16)
.
(17)
Доказательство. Пусть управляемые связи в любой из конструкций с актуаторным управлением зафиксированы. Для того, чтобы такая конструктивная структура была мгновенно неизменяема и статически определима, необходимо выполнение следующего условия:
.
Предположим теперь, что 
, тогда из (15) следует
.
(18) Будем считать, что состояние
любой 
-й 
реперной точки в
локальной системе координат 
, связанной с геометрическим центром
главного зеркала, может быть задано вектором,
и положим, что все 
реперные точки
панели с индексом зафиксированы на
стабилизируемой поверхности 
при отсутствии
возмущений, т.е. 
, 
. Остальные 
панели
составной поверхности находятся в возмущенном состоянии, при этом пространственное
положение их реперных точек (по 
на каждом -м щите) характеризуется вектором
,
(20)
в котором 
, 
– произвольный малый вектор возмущений размерности
, где 
– число неуправляемых
связей -й 
панели с ранее
установленными элементами составной поверхности.
Тогда состояние всей возмущенной конструкции, за исключением первой панели, можно описать составным вектором следующего вида:
,
(21)
где 
и размерность малого вектора 
равна 
, 
.
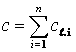Положим, что все управляемых связей освобождены и в состоянии 
все реперные точки возмущенной
конструкции лежат на стабилизируемой поверхности .
Примем также, что в окрестностях состояния для каждой реперной точки уравнение 
разрешимо относительно
одной из координат и пусть это будет координата 
. Обозначим совокупность
всех найденных таким образом координат, образующих 
-мерный вектор,
через 
.
Через 
обозначим вектор размерности 
, образуемый остальными
компонентами вектора ,
при этом 
, и
положим, что между векторами 
и имеет место функциональная взаимосвязь
вида:
,
откуда
.
(22)
Тогда считая, что функция
гладкая,
после подстановки (21) в (20) приходим к отображению вида 
:
.
Отсюда следует, что для
обеспечения управляемости любой из конструкций составной поверхности с
актуаторным управлением необходимо, чтобы у любого малого в 
в окрестности 
существовал прообраз, а это
обеспечивается только тогда, когда [6]:
,
(23)
откуда
,
что противоречит (18) и, следовательно:
,
(24)
т.е. утверждение 1 справедливо.
Согласно свойству 5,
рассмотренному ранее, любая составная управляемая с помощью актуаторов конструкция
отражателя должна быть построена так, чтобы при произвольных малых нарушениях
связей, вызванных неточностями изготовления, сборки и первичной настройки,
деформационными процессами, возникающими под влиянием гравитации, солнечной радиации,
остужающего действия ветра, аэродинамических явлений существовало бы такое
положение 
регулируемых
актуаторами связей, при котором все реперные точки зеркальных панелей находятся
на стабилизируемой поверхности .
Покажем, что в
любой из рассматриваемых многопанельных отражающих поверхностей (рис. 2) при
соблюдении числа неуправляемых и управляемых связей с учетом требований
утверждения 1, существуют такие состояния регулируемых связей, при которых
достигается требуемая точность аппроксимации составной отражающей конструкцией
заданной поверхности стабилизации . Для этого докажем утверждение.
Утверждение 2. Пусть:
–
поверхность стабилизации;
– совокупность пространственных
координат всех реперных
точек, находящихся под влиянием возмущений;
– вектор невязки реальной
поверхности аппроксимируемой составной многопанельной поверхностью и эталонной
поверхностью стабилизации , определяемый в точках,
соответствующих реперным точкам;
– вектор 
управляемых связей составной
поверхности;
– допустимое значение
среднеквадратического отклонения реальной составной отражающей
поверхности от «идеальной» .
Тогда соотношение
,
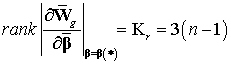(25)
где 
– состояние вектора 
, при котором вектор невязки 
,устанавливает достаточное условие управляемости составного многопанельного зеркала главного рефлектора.
Доказательство.
Известно, что в трехмерной системе координат, подобной локальной
системе координат ,
связанной с геометрическим центром главного зеркала, расстояние
между двумя точками 
и 
можно определить по формуле:
.
Как уже
упоминалось ранее, конечной целью управления формой составной отражающей
поверхности главного зеркала радиотелескопа является достижение такого пространственного положения -й реперной точки с
координатами 
, когда расстояние 
между реперной точкой и точкой 
на стабилизируемой
поверхности , в которой эта-я точка должна быть «в идеале»,
удовлетворяет следующему требованию:
, (27)
Положим, что между
вектором и макровектором
, характеризующим
невозмущенное состояние составной зеркальной поверхности, и, соответственно,
между и вектором
существует
однозначная функциональная взаимосвязь вида:
или 
.
(28)
Заметим, что это уравнение (28) описывает смещение реперных точек при точном выполнении всех неуправляемых связей.
В реальных условиях
эксплуатации возмущенное состояние -й реперной точки можно описать вектором , а возмущенное
состояние всей составной поверхности – макровектором . В силу малости вид зависимостей 
и 
не изменяется и это позволяет
записать следующее выражение:
.
(29)
Для уменьшения значений 
с целью обеспечения
условия 
в любой
из рассматриваемых конструкций составного рефлектора предусмотрена возможность
управления реальным положением реперных точек зеркальных панелей путем введения
изменения 
в
состояние вектора .
В результате вектор перейдет
в новое состояние 
,
при этом .
Положим, что функции и гладкие, при этом для любой из
конструкций составной поверхности (рис.2) в
окрестностях равновесного состояния 
для невозмущенной отражающей поверхности справедливо
соотношение
,
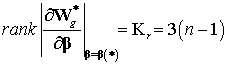(30)
где – число управляемых связей в составной
конструкции поверхности.
Здесь значение есть
то значение управляемых связей, при котором , т.е. смещение реперных точек 
.
Тогда, в силу грубости
условия (30) при достаточно малых нарушениях и малых значениях контрдеформаций 
имеет место
,
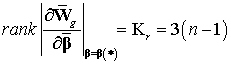(31)
т.е. в окрестностях состояния
между макровекторами 
и 
существует взаимно-однозначное
соответствие и найдется такое состояние 
, при котором будет выполнено соотношение (26).
Таким образом, выражение (31) есть достаточное условие управляемости составной конструкции отражающей поверхности, являясь, по сути, ранговым критерием управляемости подобных объектов. Следовательно, утверждение 2 доказано.
5. Синтез закона предэксплуатационной юстировки составной
отражающей поверхности
Выше (в пп. 4) было показано, что многомерный
объект регулирования – составная зеркальная поверхность управляем, поскольку
при произвольных малых отклонениях состояния реперных точек от заданной
поверхности стабилизации существует такое
положение управляемых связей, при котором ошибка регулирования стремится к
нулю, т.к. все реперные точки лежат в зоне допустимых отклонений от стабилизируемой
поверхности . Может показаться, что отсюда
вытекает простой способ юстировки пространственного положения зеркальных щитов
составной поверхности – измерить отклонения контролируемых реперных точек,
затем вычислить и выставить в нужное положение состояние управляемых связей.
Однако такой способ
юстировки неприменим в силу того, что при высокой точности контроля смещения
реперных точек, нарушения состояния любых связей (как неуправляемых, так и
управляемых), зачастую достаточно значительные, либо вообще не контролируются (неточности
изготовления и сборки неуправляемых связей) либо контролируются частично (достаточно
точные измерения текущих состояний штоков актуаторов управляемых связей при
отсутствии контроля за ошибками и деформациями сборки точек присоединения их
исполнительных механизмов в ферменному каркасу и объектам регулирования, за
линейными искажениями отражающих пластин и металлоконструкций ферменного
каркаса, вызванных гравитаций, термическими воздействиями, ветровым напором). По
этим причинам вычисление требуемого положения управляемых связей только по ошибке
регулирования – смещению реперных точек 
дает только оценочное значение характеристик
положения стержней исполнительных механизмов, определяющее некоторое исходное
состояние, с которого начинается процедура юстировки. Таким образом, функция
управляемых связей в расчетном положении не устранит ошибку регулирования.
В связи с этим предлагается итерационная процедура юстировки положения отражающих щитов составной поверхности при условии, что гравитационные нагрузки зафиксированы (чему соответствует некоторое статическое угломестное состояние главного рефлектора радиотелескопа), термическое воздействие стабилизировано (имеет место умеренно термическое состояние окружающей атмосферы в пасмурные дни, исключающие прямой нагрев зеркальных панелей солнцем), ветровой напор минимален и близок к нулю.
Очевидно, что конечной
задачей выполнения управляющих воздействий в многопанельном объекте регулирования
является достижение такого состояния 
регулирующих стержней управляемых связей с
ферменным каркасом, когда смещение 
. Этому состоянию соответствует соотношение
,
(32)
где 
– матрица параметров объекту правления, 
– матрица управлений, откуда
Введем уравнение
,
(33)
определяющее смещение по нормали реперных
точек от поверхности стабилизации при условии, когда положение
центрального сегмента поверхности зафиксировано и задано положение регулируемых связей. Обозначим через 
состояние управляемых связей на 
-м такте процесса
позиционирования зеркальных панелей составной конструкции, а через 
– соответствующее
смещение реперных точек.
Тогда уравнение линейного
приближения на -м
такте для системы (19) примет следующий вид
. (34)
Положим, что матрица невырождена и закон
управления имеет линейный вид и реализуется в форме, учитывающем информацию о
задающем воздействии, каковым следует считать величину смещения реперных точек:
,
(35)
где 
– матрица обратных связей по задающему воздействию, при этом считается справедливой гипотеза
о полной измеримости компонентов .
Отсюда следует
.
(36)
Из [7] известно, что система
(33) с регуляторами (35) асимптотически устойчива (в малом) относительно
состояния равновесия, когда асимптотически устойчива система (36). Тогда задача
стабилизации формы многоэлементной отражающей поверхности заключается в выборе
такой матрицы ,
при которой все собственные значения 
матрицы 
удовлетворяют
условию 
.
Укажем класс законов
управления, обеспечивающий асимптотическую устойчивость рассматриваемой системы
в окрестности стабилизируемой поверхности .
Введем вспомогательную
невырожденную матрицу 
и
положим, что возможен такой выбор матрицы , что
.
(37)
Тогда из (36) получим
,
(38)
откуда следует, что при 
асимптотическая
устойчивость системы (33) с регуляторами (35) и равенство
(39)
будут обеспечены, и закон управления (33) примет вид
.
(40)
Итерационная процедура
позиционирования многопанельной зеркальной поверхности имеет конечное число 
шагов в силу наличия
допустимого значения среднеквадратической ошибки отклонения пространственного положения
реперных точек пластин от поверхности стабилизации . Положим, что задано
некоторое начальное состояние отклонения 
, с которого запускается процесс
регулировки формы составной поверхности и пусть при заданной на -м шаге юстировки получим 
. Т.к. в силу (38) 
есть
,
то, положив
,
(41)
можно определить число итераций , требуемых для
достижения состояния составной поверхности :
,
(42)
где 
– целая часть числа.
Заметим, что закон управления (40) обеспечивает позиционирование состояния составной поверхности главного рефлектора как цельного объекта регулирования, т.е. соответствует централизованной схеме управления,
6. Заключение
В данной статье описаны конструктивные особенности многоэлементных зеркальных поверхностей главных антенн больших полноповоротных радиотелескопов наземного базирования с каркасно-ферменным основанием рефлектора. Обрисованы базовые схемы построения составных поверхностей с использованием гексагональных и трапецеидальных зеркальных пластин, сформированы схемы сборки поверхностей, приводящие к минимальным нарушениям при присоединении к ранее собранным поверхностным сегментам. Установлены необходимые и доставочные условия геометрической неизменяемости составной пространственной конструкции зеркала главного рефлектора.
Введены структурные свойства составных поверхностей как объекта управления и показано, что любая из рассмотренных конструкций составной поверхности (на основе гексагональных или трапецеидальных пластин), использующая три связи каждой панели с ферменным каркасом для управления формой, ведет себя как статически определенное жесткое тело с управляемой пространственной поверхностной фигурой, т.к. при фиксации в требуемом положении на поверхности стабилизации реперных точек одной из панелей и произвольных малых неточностях изготовления, сборки, остаточных термических, ветровых и иных деформациях существует такое положение управляемых связей, при котором все остальные реперные точки других отражающих щитов лежат на стабилизируемой поверхности.
Определено достаточное условие управляемости составной многоэлементной конструкции зеркала в виде рангового критерия, согласно которому количество регулируемых связей должно быть равно половине общего количества межэлементных связей.
Сформирован итерационный закон выполнения юстировки положения щитов составной отражающей поверхности, обеспечивающий асимптотическую устойчивость составного зеркала вблизи поверхности стабилизации.
Литература
1. Jacob W.M. Baars. the paraboloidal reflector antenna in radio astronomy and communication theory and practice.//astrophysics and space science library. v.348. – New York, Springer Science+Business Media, LLC. 2007. – 253p.
2. Grue G., Alvito G., Ambrosini R., etc. The Sardinia Radio Telescope. // Memorie Societa Astronomica Italiana Supplementi, 2004, Vol. 5 – P.351-356.
3. Orfei A., Morsiani M., Zacchiroli G., etc. The Active Surface System on the Noto Radio Telescope.//the 6th European VLBI Network Symposium, June 25th-28th 2002, Bonn, Germany – P.13-16.
4. Woody D. Sensitivity of Edge Sensors to Zernike Modes.// Technical Report 12, CCAT Memo Series, 2005. – 10 p.
5. Шевченко Д.В. Конечно-элементное моделирование и исследование проблем механики радиотелескопа рт-70. – Автореф. дисс….канд.техн.наук. – СПб.: СПбГПУ, 2005. – 17с.
6. Стернберг C. Лекции по дифференциальной геометрии. Пер. с англ. – М., Мир, 1970. – 412с.
7. Бромберг П.В. Матричные методы в теории релейного и импульсного регулирования. – М.: Наука, 1967. – 324с.