УДК 621.391
ОЦЕНКА ПАРАМЕТРОВ ФРАКТАЛОВ В СМЕСИ ХАОТИЧЕСКИХ СИГНАЛОВ ПО СПЕКТРУ МОЩНОСТИ
С. А. Останин
Алтайский государственный университет, г. Барнаул
Получена 10 мая 2012 г.
Аннотация. Приводятся результаты спектрального анализа смеси хаотических сигналов. Аналитически показано, что по спектру мощности можно обнаружить наличие фрактального сигнала в смеси с шумом и выполнить оценку параметров фрактала. Приведены результаты спектрального анализа тестового акустического сигнала и определена его фрактальная размерность.
Ключевые слова: фракталы, спектральный анализ.
Abstract. The results of spectral analysis of a mixture of chaotic signals. It is shown analytically that the power spectrum can detect the presence of a fractal signal mixed with noise and perform parameter estimation of the fractal. The results of spectral analysis of the acoustic signal and the test is defined by its fractal dimension.
Keywords: fractals, spectral analysis.
Многие процессы природе протекают таким образом, что их динамические переменные представляют собой функции с дробной размерностью (в том числе, фракталы). В работе [1] представлен обзор использования фракталов и дробных операторов в радиотехнике и электронике. Методы фрактального анализа используют в разных областях биологии и медицины [2-8].
С целью повышения отношения сигнал/шум, при регистрации сигнала осуществляют фильтрацию. В случае, когда шум или сигнал занимают узкую полосу, а так же в случае, когда сигнал и шум занимают неперекрывающиеся участки спектра, эта задача решается просто. Если сигнал представляет собой фрактал, шум и сигнал обычно имеют перекрывающиеся полосы спектра. Однако, используя тот факт, что спектр мощности фрактального сигнала имеет характерный вид, спектральный анализ можно использовать для оценки параметров сигнала, например, фрактальной размерности.
Пусть наблюдаемая
величина 
представляет собой аддитивную смесь
сигналов 
и 
:
. (1)
В отношении сигналов и известно,
что они представляют собой случайные функции полученные в результате
дифференцирования или интегрирования белого шума.
Пусть Фурье образы сигналов и имеют
вид:
, (2)
, (3)
где i – мнимая единица; 
– круговая частота; 
, 
– параметры,
характеризующие порядок (в том числе дробный) производной или интеграла белого
шума; 
, 
– параметры,
определяющие интегральную мощность сигналов. Спектры мощности 
и 
сигналов
и имеют
вид
, (4)
. (5)
В работах [9-10] показано, что при 
и 
сигнал
представляет собой фрактал, фрактальная
размерность 
которого определяется как
Следовательно, по спектру
мощности наблюдаемой величины можно определить
наличие или отсутствие фрактала в сумме сигналов , и определить его размерность.
Фурье образ 
функции , в
силу линейности Фурье преобразования, имеет вид
.
(7)
Спектр мощности 
функции определятся
как
. (8)
Найдем и 
Фурье образа . Учитывая, что
,
выражение (7) можно записать как
,
следовательно
, (9)
. (10)
Подставляя (9) и (10) в (8) получим:
Введем обозначения:
,
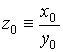. (11)
С учетом (11) можно
записать как
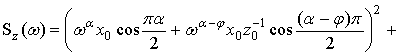
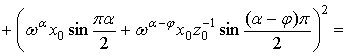
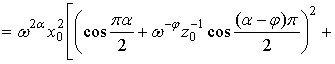
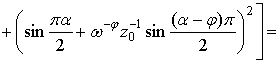
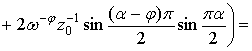
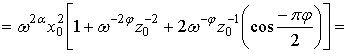
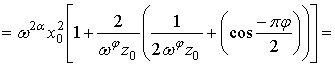
. (12)
Как видно из (12), спектр мощности суммы фрактальных сигналов симметричен
относительно параметров обоих сигналов. Параметры , , , найти из спектр мощности при 
, 
или , 
не представляется возможным. При , и 
выражение (12) имеет вид
. (13)
Прологарифмируем уравнение (13) и
найдем параметры , 
одного
из сигналов:
. (14)
Функцию 
можно
получить в результате линейной аппроксимации функции 
при
. Параметр находим
из (14) по двум значениям на разных частотах 
и 
:
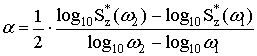. (15)
Параметр находим
из (14) при условии 
:
. (16)
Параметры и
второго сигнала определяем аналогично,
аппроксимируя линейной функцией
(17)
при 
.
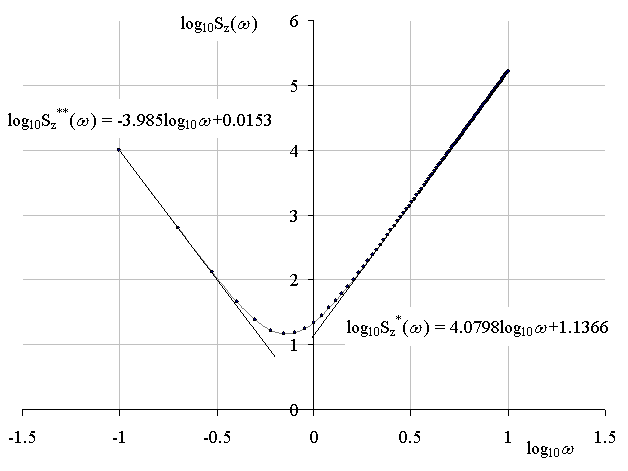
Рис. 1. Спектр мощности суммы
сигналов разной фрактальной размерности с параметрами 
,
, 
, 
.
На рисунке 1 показан пример
спектра мощности (в логарифмическом масштабе) суммы сигналов и Фурье
образы которых имеют вид
и 
. (18)
В результате линейной аппроксимации спектра
мощности получены уравнения
, (19)
. (20)
Используя (15) и (16), из уравнений (19)
и (20) получены значения параметров 
, 
, 
. Этот результат хорошо согласуется со
значениями параметров спектров 
, 
(15).
Для анализа реальных
сигналов в среде визуального программирования LabVIEW был создан генератор суммы акустических случайных сигналов (рисунок 2) и (рисунок
3) со спектрами мощности 
и 
. На рисунке 4 показан сигнал 
, поступающий на акустический излучатель.
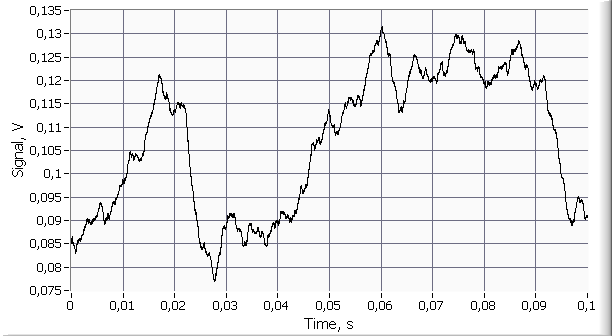
Рис. 2. Сигнал с 
.
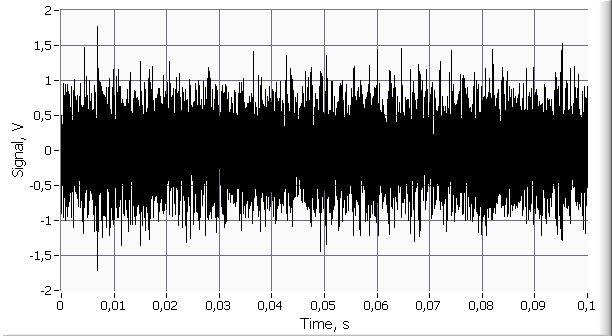
Рис. 3. Сигнал с 
.
Рис. 4. Сигнал .
Упрощенная схема
установки для передачи сигнала по акустическому
каналу и анализа показана на рисунке 5. Акустический излучатель 1 был
расположен на расстоянии 1м от микрофона 2. Сигнал микрофона поступал на вход
звуковой карты компьютера. Компьютер рассчитывал спектр мощности сигнала
микрофона в логарифмическом масштабе (рисунок 6), усреднял его по 500
реализациям, осуществлял линейную аппроксимацию и оценивал параметры , случайных
сигналов и .
Рис. 5. Схема установки для передачи
сигнала по акустическому каналу: 1 –
акустический излучатель, 2 – микрофон.
Рис. 6.
Спектр мощности сигнала микрофона усредненный по 500 реализациям.
В результате
автоматического анализа спектра мощности акустического сигнала были получены 
и 
.
Относительное отклонение оценки параметров и от заданных значений (– 1.45 и 1.45)
составило около одного процента. В соответствии с (6) значение параметра одного из сигналов соответствует
фрактальной размерности D =1.04
(значению исходной компоненты смеси соответствует
фрактальная размерность D =1.05).
Таким образом, установлено что анализ спектра мощности позволяет оценивать
независимые параметры хаотических сигналов с различными статистическими
свойствами в аддитивной смеси.
Литература
1. Потапов А.А. Фракталы, скейлинг и дробные операторы в радиотехнике и электронике: современное состояние и развитие // № 1, 2010, М.: ИРЭ РАН. http://jre.cplire.ru/jre/jan10/4/text.html
2. M. E. Dokukin, N. V. Guz, R. M. Gaikwad, C. D. Woodworth, I. Sokolov. Cell Surface as a Fractal: Normal and Cancerous Cervical Cells Demonstrate Different Fractal Behavior of Surface Adhesion Maps at the Nanoscale // Phys. Rev. Lett., 2011, V.107, 028101.
3. Phinyomark А., Phukpattaranont P. et. all. Electromyography (EMG) signal classification based on detrended fluctuation // Fluctuation and Noise Letters, 2011, V.10, № 3, p.281-301
4. Исаева В.В., Каретин Ю.А., Чернышев А.В., Шкуратов Д.Ю. Фракталы и хаос в биологическом морфогенезе / Институт биологии моря ДВО РАН, 2004, 128 с.
5. Waliszewski P., Konarski J. Neuronal differentiation and synapse formation occur in space and time with fractal dimension // Synapse. 2002. V. 43. P. 252-258.
6. Лебедева Н.Н., Бецкий О.В. Фракталы в биологии и медицине // Биомедицинские технологии и радиоэлектроника, №10, 2002. с.49-59.
7. Крестьева И.Б., Цыганов М.А., Асланиди Г.В.,Медвинский А.Б., Иваницкий Г.Р. Фрактальная самоорганизация в популяциях бактерий Escherichia coli: экспериментальное исследование // ДАН. 1996. Т. 351, № 3, с. 406-409.
8. Havlin S., Buldyrev S.V. et all. Fractals in Biology and Medicine // Chaos. Solitons & Fractals, 1995, V.6, p.171-201.
9. Berry M.V. Diffractals // J. Phys. A. 1979. V.12. N6, p. 781-797.
10. Berry M.V., Lewis Z.V. On the Weierstrass-Mandelbrot fractal function. // Proc. R. Soc. Lond., 1980, A 370, р.459-484.