УДК 538.975
АНИЗОТРОПИЯ ТЕМПЕРАТУРНЫХ ХАРАКТЕРИСТИК МАГНИТОСТАТИЧЕСКИХ ВОЛН В ПЛАНАРНЫХ ФЕРРИТАХ
В. В. Шагаев
Московский государственный технический университет им. Н.Э. Баумана, Калужский филиал
Получена 16 апреля 2012 г.
Аннотация. Обсужден вопрос о влиянии анизотропных свойств ферритовой пленки на температурные коэффициенты частот основных типов магнитостатических волн. Детально исследованы пленки с кубической магнитной анизотропией и волна поверхностного типа. Установлено, что при намагничивании вдоль оси <100> температурные зависимости намагниченности насыщения и поля анизотропии частично, а в отдельных случаях полностью, компенсируют друг друга, повышая термостабильность частот. Приведены результаты экспериментальных исследований пленок железоиттриевого граната.
Ключевые слова: магнитостатическая волна, ферриты, железоиттриевый гранат, магнитная анизотропия, намагниченность, температурный коэффициент частоты.
Abstract. The question about influence of anisotropic properties of a ferrite film upon temperature coefficients of the basic types of magnetostatic waves is discussed. Films with cubic magnetic anisotropy and surface type of the wave are investigated in details. It is revealed that at magnetization along a <100> axis the temperature dependences of saturation magnetization and of anisotropy field partially, and in some cases completely, compensate each other, increasing thermostability of frequencies. Results of experimental investigations of yttrium iron garnet films are given.
Keywords: magnetostatic wave, ferrites, yttrium iron garnet, magnetic anisotropy, magnetization, temperature coefficient of frequency.
Введение
Обработка сверхвысокочастотных сигналов с помощью магнитостатических спиновых волн (МСВ) относится к перспективным направлениям развития электроники [1]. Основу МСВ-устройств составляют пленки ферритов, выращенные на подложках немагнитных кристаллов [2]. При этом используются ферриты с малым затуханием спиновых возбуждений. Также важно, чтобы магнитные параметры феррита слабо зависели от температуры. Попытки создать материал, удовлетворяющий обоим требованиям, пока не увенчались успехом. Из всех известных ферритов самым малым затуханием спиновых волн обладает железоиттриевый гранат (ЖИГ, Y3Fe5O12). Однако температурная зависимость намагниченности насыщения у ЖИГ такова, что требуются дополнительные меры по обеспечению термостабильности устройств. Как правило, высокая стабильность достигается усложнением конструкции [3, 4], применением дополнительных узлов и (или) электронных схем, осуществляющих термокомпенсацию. Вместе с тем одним из факторов, определяющих характеристики МСВ, является магнитная анизотропия феррита [5]. Поэтому уместна постановка вопроса об использовании полей анизотропии в качестве средства термостабилизации характеристик. Пленкам, выращенным на монокристаллических подложках, присущи два основных вида анизотропии – кристаллографическая и одноосная. К настоящему времени проявления анизотропии в спектрах МСВ достаточно подробно исследованы. Тем не менее, вопрос о масштабах влияния полей анизотропии на температурные изменения спектров все еще остается в стадии разработки. В данной статье изложены результаты исследований, позволяющие провести сравнительный анализ влияния температурной зависимости намагниченности насыщения и обоих видов полей анизотропии на температурные коэффициенты частот основных типов МСВ. Акцент в исследовании был сделан на поиске путей повышения термостабильности частот.
Модель пленки
Температурный коэффициент частоты (ТКЧ) МСВ с заданным значением волнового числа рассчитывался по формуле (f – частота МСВ, T – температура)
 .
.
Выражения для ТКЧ были выведены из законов дисперсии МСВ путем их дифференцирования по температуре. При этом были использованы законы дисперсии, полученные совместным интегрированием уравнений Максвелла, взятых в магнитостатическом приближении и с соответствующими электродинамическими граничными условиями, и линеаризованного уравнения движения намагниченности без учета обмена и потерь (уравнения Ландау-Лифшица). Эффективное поле магнитной анизотропии рассчитывалось на основе выражения для плотности энергии магнитной анизотропии
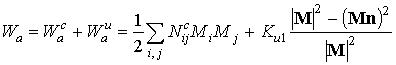 .
.
Здесь кристаллографическая анизотропия
учтена в наиболее общем виде – посредством тензора эффективных размагничивающих
факторов ![]() , а одноосная – посредством константы Ku1
(n – нормаль к пленке). Вектор
намагниченности феррита M
имеет статическую (M0)
и переменную (m) составляющие,
так что
, а одноосная – посредством константы Ku1
(n – нормаль к пленке). Вектор
намагниченности феррита M
имеет статическую (M0)
и переменную (m) составляющие,
так что ![]() . Компоненты тензора
. Компоненты тензора ![]() и вектора намагниченности Mi
взяты
в системе координат xyz
с осью z || M0.
Тогда в линейном по m
приближении имеем:
и вектора намагниченности Mi
взяты
в системе координат xyz
с осью z || M0.
Тогда в линейном по m
приближении имеем: ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Для проведения
физически ясного анализа в модель были введены ограничения. Полагалось, что
вектор статической намагниченности M0
направлен вдоль кристаллографической оси симметрии не ниже третьего порядка. Анализ
показывает, что в этом случае из инвариантности энергии относительно
преобразований симметрии следуют равенства: ![]() и
и ![]() , если
, если ![]() . При
этом в дисперсионных уравнениях МСВ кристаллографическая анизотропия может быть
учтена с помощью единственного параметра:
. При
этом в дисперсионных уравнениях МСВ кристаллографическая анизотропия может быть
учтена с помощью единственного параметра: ![]() . Уместно
отметить, что кристаллическая решетка ЖИГ имеет оси симметрии второго, третьего
и четвертого порядка, и влияние поля кристаллографической анизотропии на
спектры МСВ оказывается экстремальным при намагничивании именно вдоль
высокосимметричных осей.
. Уместно
отметить, что кристаллическая решетка ЖИГ имеет оси симметрии второго, третьего
и четвертого порядка, и влияние поля кристаллографической анизотропии на
спектры МСВ оказывается экстремальным при намагничивании именно вдоль
высокосимметричных осей.
Одноосная магнитная
анизотропия в рассматриваемой модели обусловлена плотностью энергии ![]() , где q – угол наклона
вектора намагниченности к пленке. В данной работе была использована геометрия с
, где q – угол наклона
вектора намагниченности к пленке. В данной работе была использована геометрия с
![]() (касательное намагничивание) и
(касательное намагничивание) и ![]() (перпендикулярное). Кроме того, при
проведении расчетов был введен параметр
(перпендикулярное). Кроме того, при
проведении расчетов был введен параметр ![]() (поле
одноосной анизотропии).
(поле
одноосной анизотропии).
«Привязка» ориентации вектора M0
как к оси симметрии кристалла, так и к одной из двух предельных ориентаций
относительно плоскости пленки позволяет упростить расчет ТКЧ. В этом случае
будем полагать, что направление M0
совпадает с направлением вектора напряженности намагничивающего поля, и при
этом температурные изменения магнитных параметров феррита не приводят к
изменению направления вектора M0.
Следовательно, при расчете ТКЧ отпадает необходимость учета температурных
производных от углов, задающих ориентацию M0.
Угловые переменные входят в дисперсионные уравнения МСВ как в явном виде, так и
в составе выражений для ![]() . Вместе с тем кристаллографическая
ориентация пленки не может быть произвольной, так как либо нормаль к пленке,
либо одно из касательных направлений должны совпадать с кристаллографической осью
симметрии высокого порядка.
. Вместе с тем кристаллографическая
ориентация пленки не может быть произвольной, так как либо нормаль к пленке,
либо одно из касательных направлений должны совпадать с кристаллографической осью
симметрии высокого порядка.
Вывод выражений для температурных коэффициентов частот
В рамках сформулированной модели можно выполнить аналитический расчет ТКЧ для основных типов МСВ.
1. Прямые объемные МСВ (ПОМСВ).
В этом случае векторы напряженности внешнего намагничивающего поля Hex и равновесной намагниченности M0 направлены перпендикулярно пленке (M0 || Hex || n).
Дисперсионное уравнение (ДУ) ПОМСВ имеет вид
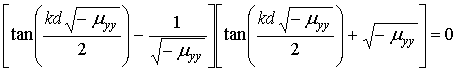 . (1)
. (1)
Здесь k – модуль волнового вектора k, d – толщина пленки, µyy – компонента тензора магнитной проницаемости в системе координат xyz с направлениями осей z || M0 и у || k. Расчет µyy из уравнения Ландау-Лифшица для рассматриваемой модели пленки приводит к следующему выражению
 , (2)
, (2)
где ![]() ; g
– гиромагнитное отношение (в расчетах полагалось g
= 2.8 MHz/Oe).
; g
– гиромагнитное отношение (в расчетах полагалось g
= 2.8 MHz/Oe).
Уравнение (1) разбивается на два ДУ – одно для симметричных, а другое для антисимметричных мод. В частности, для основной моды, относящейся к симметричному типу, получим
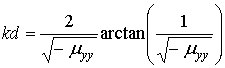 . (3)
. (3)
Именно для этой моды был рассчитан ТКЧ.
Из (2) следует
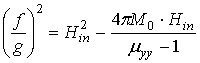 . (4)
. (4)
Уравнения (3) и (4) задают
дисперсионную зависимость f(kd) в параметрическом виде. Компонента µyy играет роль промежуточного параметра со значениями, лежащими в интервале
![]() . Рассматривая µyy именно в таком
качестве и дифференцируя (4), получим ТКЧ
. Рассматривая µyy именно в таком
качестве и дифференцируя (4), получим ТКЧ
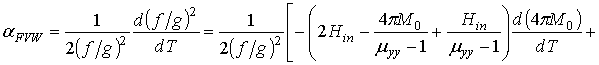
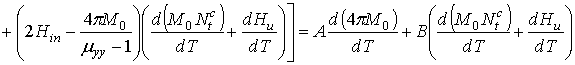 .
(5)
.
(5)
Последнее равенство отображает структуру выражения ТКЧ.
На рис. 1 приведены примеры зависимостей, рассчитанных по формулам (3), (5) и дающие представление о влиянии полей магнитной анизотропии на ТКЧ. В частности отметим, что из (5) следует неравенство
![]() ,
,
так что для существенности влияния
необходимо, чтобы производные ![]() и
и ![]() были сравнимы с
были сравнимы с ![]() .
.
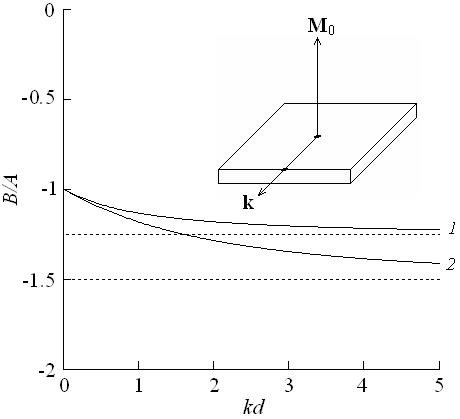
Рис.
1. Зависимости, характеризующие вклады полей анизотропии пленочного феррита в
ТКЧ основной моды ПОМСВ. Значения параметров: 1 – ![]() ; 2 –
; 2 – ![]() .
Асимптотические значения
.
Асимптотические значения ![]() (
(![]() ) изображены точечными линиями.
) изображены точечными линиями.
2. Обратные объемные МСВ (ООМСВ).
В этом случае вектор M0,
направлен касательно к пленке, и волна распространяется вдоль этого
касательного направления (![]() и
и ![]() ).
).
Законы дисперсии симметричных и антисимметричных мод задаются уравнением
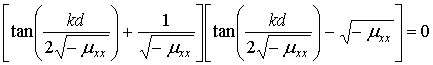 , (6)
, (6)
где μxx – компонента тензора магнитной проницаемости в системе координат xyz с осями z || M0 и x || n.
Аналогично анализу ПОМСВ будем
рассматривать μxx как параметр со
значениями ![]() . Тогда закон дисперсии основной моды ООМСВ
(антисимметричной) будет задан в виде параметрической зависимости
. Тогда закон дисперсии основной моды ООМСВ
(антисимметричной) будет задан в виде параметрической зависимости
![]() , (7)
, (7)
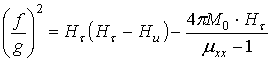 , (8)
, (8)
где ![]() .
.
Из (8) получим выражение для ТКЧ

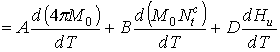 . (9)
. (9)
В отличие от предыдущего
случая производные ![]() и
и ![]() входят
в выражение ТКЧ с разными коэффициентами. Анализ выражения показывает, что в
важной для практики длинноволновой части спектра (когда согласно (7)
входят
в выражение ТКЧ с разными коэффициентами. Анализ выражения показывает, что в
важной для практики длинноволновой части спектра (когда согласно (7) ![]() ) большие значения
) большие значения ![]() реализуются в полях
реализуются в полях ![]() . И даже если
. И даже если ![]() , то влияние
поля кристаллографической анизотропии может оказаться существенным.
, то влияние
поля кристаллографической анизотропии может оказаться существенным.
Вклад одноосной анизотропии в
ТКЧ характеризуется отношением ![]() , которое по уравнению
(7) зависит только от kd. Причем, если
, которое по уравнению
(7) зависит только от kd. Причем, если ![]() , то
, то ![]() . Так что в длинноволновой части спектра
ООМСВ влияние одноосной анизотропии на ТКЧ будет определяться соотношением
производных
. Так что в длинноволновой части спектра
ООМСВ влияние одноосной анизотропии на ТКЧ будет определяться соотношением
производных ![]() и
и ![]() . На
рис. 2 приведены примеры зависимостей, рассчитанных на основе уравнений (7) и (9).
. На
рис. 2 приведены примеры зависимостей, рассчитанных на основе уравнений (7) и (9).
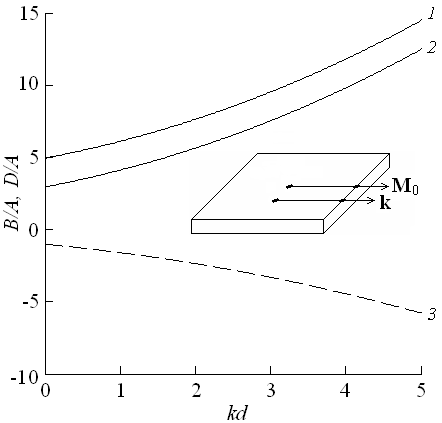
Рис. 2.
Зависимости, характеризующие вклады полей анизотропии пленочного феррита в ТКЧ
основной моды ООМСВ. Сплошные кривые 1, 2 изображают отношение В/А,
пунктирная 3 – отношение D/A.
Значения параметров: 1 – ![]() ; 2 –
; 2 – ![]() , 3 – не зависит от
, 3 – не зависит от ![]() . Полагалось, что
. Полагалось, что ![]() ,
но без наложения ограничений на значение производной
,
но без наложения ограничений на значение производной ![]() .
.
3. Поверхностная магнитостатическая волна (ПМСВ).
Вектор M0
направлен касательно к пленке, и волна распространяется перпендикулярно этому
направлению (![]() ,
, ![]() и,
по-прежнему,
и,
по-прежнему, ![]() ).
).
Для небольших полей одноосной анизотропии, когда ![]() и
и ![]() (но
без ограничений на значения
(но
без ограничений на значения ![]() ), ДУ поверхностной МСВ
имеет вид [6]
), ДУ поверхностной МСВ
имеет вид [6]
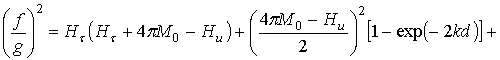
![]() , (10)
, (10)
где функция ![]() задана выражением
задана выражением
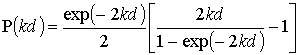 .
.
Из (10) путем дифференцирования по температуре получим выражение для ТКЧ поверхностной МСВ
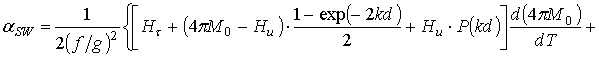
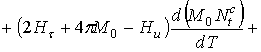
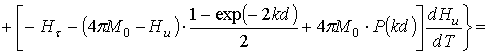
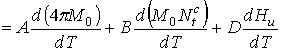 . (11)
. (11)
Графический анализ формулы приведен на рис. 3.
Видно, что влияние поля кристаллографической
анизотропии будет наиболее существенным в длинноволновой части спектра и в слабых
намагничивающих полях, когда ![]() .
.
Относительный вклад поля одноосной анизотропии
характеризуется приближенным равенством ![]() (точным
на границах спектра), так что влияние одноосной анизотропии на ТКЧ будет
определяться соотношением производных
(точным
на границах спектра), так что влияние одноосной анизотропии на ТКЧ будет
определяться соотношением производных ![]() и
и ![]() .
.
Подытоживая результаты
данного раздела, отметим, что проведенный анализ основывался на наиболее общем
описании кристаллографической магнитной анизотропии. Для получения численных
значений ТКЧ необходимо конкретизировать выражение ![]() ,
связав его с материальными параметрами феррита и типом оси симметрии. При этом наибольший
интерес представляют ферриты с кубической симметрией кристаллической решетки и
оси симметрии третьего и четвертого порядка.
,
связав его с материальными параметрами феррита и типом оси симметрии. При этом наибольший
интерес представляют ферриты с кубической симметрией кристаллической решетки и
оси симметрии третьего и четвертого порядка.
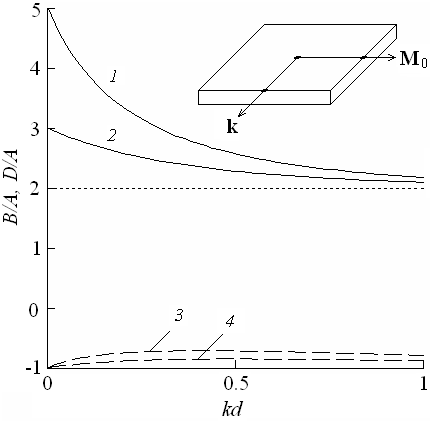
Рис.
3. Зависимости, характеризующие вклады полей анизотропии пленочного феррита в
ТКЧ поверхностной МСВ. Кривые 1, 2 изображают отношение В/А;
3, 4 – D/A.
Значения параметров: 1, 3 – ![]() ; 2,
4 –
; 2,
4 – ![]() . Полагалось, что
. Полагалось, что ![]() и
и
![]() , но без ограничений на значение
производной
, но без ограничений на значение
производной ![]() .
.
Поверхностная МСВ в пленке с кубической магнитной анизотропией
Знание зависимости эффективных размагничивающих факторов от углов, определяющих ориентацию вектора намагниченности относительно кристаллической решетки, позволяет детализировать исследование. В частности, появляется возможность сравнивать между собой характеристики МСВ для направлений намагничивания вдоль осей симметрии разного порядка.
Вывод необходимых угловых зависимостей был построен на основе выражения для плотности энергии кубической магнитной анизотропии. Инвариантное к преобразованиям симметрии кристаллической решетки выражение, учитывающее лишь одну, как правило, наибольшую константу, имеет вид [7]

Здесь ![]() –
первая константа кубической магнитной анизотропии, а суммирование производится
по проекциям вектора намагниченности на оси системы координат, образованной
осями симметрии кристалла четвертого порядка. В системе координат xyz с осью z || M0 и при произвольной ориентации M0 диагональные компоненты
тензора
–
первая константа кубической магнитной анизотропии, а суммирование производится
по проекциям вектора намагниченности на оси системы координат, образованной
осями симметрии кристалла четвертого порядка. В системе координат xyz с осью z || M0 и при произвольной ориентации M0 диагональные компоненты
тензора ![]() имеют вид
имеют вид
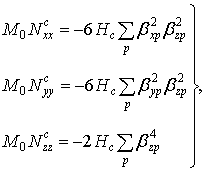
где ![]() –
эффективное поле кубической анизотропии, βip – косинусы
углов, образованных координатными осями i = x, y, z
с осями кристалла p = [100], [010], [001]. Из этих выражений был
рассчитан параметр
–
эффективное поле кубической анизотропии, βip – косинусы
углов, образованных координатными осями i = x, y, z
с осями кристалла p = [100], [010], [001]. Из этих выражений был
рассчитан параметр ![]() для направлений вектора M0 вдоль высокосимметричных
осей типа <100> и <111>.
для направлений вектора M0 вдоль высокосимметричных
осей типа <100> и <111>.
Пусть z || M0 || [001]. Тогда
![]() .
.
После подстановок и простейших вычислений получим
![]() . (12)
. (12)
Очевидно, что выведенные равенства можно использовать для любой оси типа <100>.
Аналогичный расчет был
выполнен для M0 ||
<111>. Полагая z || M0 || [111] и ![]() , получим окончательно
, получим окончательно
![]() . (13)
. (13)
Выражения (12) и (13) могут быть использованы для подстановок в формулы (5), (9), (11).
Наибольший практический интерес представляет ПМСВ. Поверхностная волна имеет только одну моду и более эффективно, чем объемные волны, возбуждается с помощью микрополоскового преобразователя. Для удобства проведения анализа ТКЧ поверхностной волны преобразуем (11) к виду

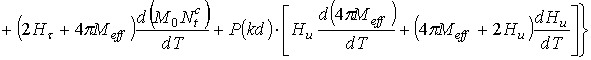 , (14)
, (14)
где ![]() –
эффективная намагниченность. Анизотропия ТКЧ в плоскости пленки обусловлена
слагаемыми с производными
–
эффективная намагниченность. Анизотропия ТКЧ в плоскости пленки обусловлена
слагаемыми с производными ![]() и
и ![]() , так как параметр
, так как параметр ![]() (входящий,
в том числе, в выражение для Hτ) зависит от
кристаллографической ориентации вектора M0. Слагаемые, объединенные квадратными скобками с
множителем P(kd), изотропны. Кроме того, в ряде случаев (например, в
устройствах на основе пленок ЖИГ) можно полагать, что
(входящий,
в том числе, в выражение для Hτ) зависит от
кристаллографической ориентации вектора M0. Слагаемые, объединенные квадратными скобками с
множителем P(kd), изотропны. Кроме того, в ряде случаев (например, в
устройствах на основе пленок ЖИГ) можно полагать, что![]() и
и
![]() . Тогда с учетом того, что функция P(kd)
имеет максимум со значением
. Тогда с учетом того, что функция P(kd)
имеет максимум со значением ![]() , выражение (14) можно
использовать в нулевом по параметрам
, выражение (14) можно
использовать в нулевом по параметрам ![]() и
и ![]() приближении.
приближении.
Примеры расчетов ТКЧ,
выполненных по формуле (14) с подстановками (12) и (13) приведены на рис. 4, 5.
При этом рис. 4 демонстрирует чувствительность ТКЧ к кристаллографической
ориентации вектора M0, а рис.
5 – к температурному коэффициенту ![]() и к напряженности
намагничивающего поля Hex. Отметим, что в примерах полагалось
и к напряженности
намагничивающего поля Hex. Отметим, что в примерах полагалось ![]() , так что масштаб плоскостной анизотропии
ТКЧ определяется исключительно производной
, так что масштаб плоскостной анизотропии
ТКЧ определяется исключительно производной ![]() . Причем
оказалось, что значения этой производной могут компенсировать гораздо большие
значения производной
. Причем
оказалось, что значения этой производной могут компенсировать гораздо большие
значения производной ![]() . В условиях полной компенсации
зависимости на рис. 5 проходят через нулевое значение.
. В условиях полной компенсации
зависимости на рис. 5 проходят через нулевое значение.
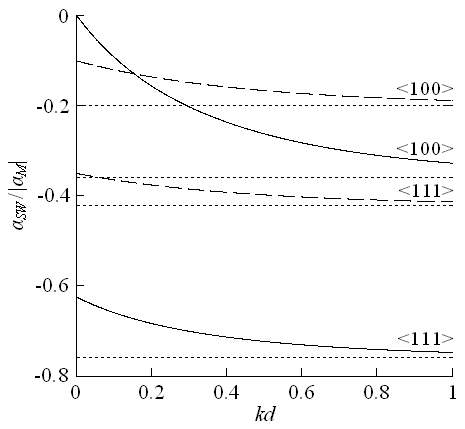
Рис. 4. Нормированный
температурный коэффициент частоты ПМСВ для двух кристаллографических ориентаций
вектора постоянной намагниченности (указаны на кривых). Полагалось: 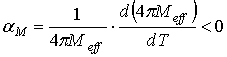 ;
;  ;
; 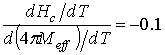 ;
; 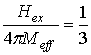 –
сплошные кривые;
–
сплошные кривые; 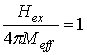 – пунктирные. Асимптотические
значения – точечные.
– пунктирные. Асимптотические
значения – точечные.

Рис. 5. Полагалось: M0 ||
<100> ;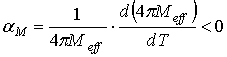 ;
;  .
.
Таблица 1
Параметры, использованные при расчете зависимостей на рис. 5.
|
№ кривой |
|
|
|
1 |
- 0.10 |
1/3 |
|
2 |
- 0.11 |
1/3 |
|
3 |
- 0.10 |
1/4 |
Термостабилизация частот из спектра поверхностной МСВ
Возможность обращения ТКЧ в ноль имеет большое практическое значение. Поэтому был проведен подробный анализ необходимых условий.
Рассмотрим пленку с
кристаллографической ориентацией {110}. В плоскости такой пленки расположены
оба типа высокосимметричных осей – <100> и <111>. Используем
формулу (14) для анализа знака ТКЧ. По-прежнему ограничимся нулевым приближением
по параметрам ![]() и
и ![]() . Кроме
того, полагаем, что
. Кроме
того, полагаем, что ![]() и
и ![]() . Оба
неравенства выполняются, например, в пленках ЖИГ. Тогда для ориентации M0 || <111> из (14) с
подстановкой (13) следует
. Оба
неравенства выполняются, например, в пленках ЖИГ. Тогда для ориентации M0 || <111> из (14) с
подстановкой (13) следует
![]() . (15)
. (15)
Потребуем для M0 || <100> выполнения противоположного неравенства
![]() . (16)
. (16)
В этом случае между осями <111> и <100> будет расположено направление намагничивания с нулевым значением ТКЧ. Исследуем условия выполнения (16). Выражение (14) с подстановкой (12) и алгебраические преобразования приводят к следующему условию положительности значений ТКЧ для ориентации M0 || <100>
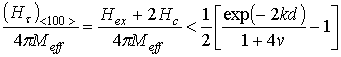 , (17)
, (17)
где
 .
.
В соответствии со знаками производных отношение
v отрицательно (v
< 0), и вместе с тем при выводе (17) полагалось ![]() (что
имеет место, например, в ЖИГ). При возрастании kd правая часть
неравенства (17) из положительной становится отрицательной, тогда как левая
всегда положительна. Следовательно, неравенство может быть удовлетворено в
ограниченном интервале значений kd, расположенном вблизи длинноволновой
границы спектра ПМСВ. Из (17) следует также ограничение на значения Hex.
Полагая
(что
имеет место, например, в ЖИГ). При возрастании kd правая часть
неравенства (17) из положительной становится отрицательной, тогда как левая
всегда положительна. Следовательно, неравенство может быть удовлетворено в
ограниченном интервале значений kd, расположенном вблизи длинноволновой
границы спектра ПМСВ. Из (17) следует также ограничение на значения Hex.
Полагая ![]() , получим
, получим
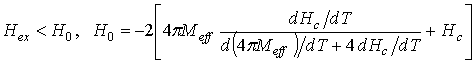 . (18)
. (18)
В частности, оценка значения H0
для ЖИГ дает: ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Для сравнения заметим, что в модели пленки из изотропного феррита, помещенного в касательное намагничивающее поле, ТКЧ поверхностной МСВ всегда имеет отрицательное значение. При этом модель изотропного феррита, как правило, применяется к пленкам с ориентацией типа {111}. В анизотропном же материале и пленках с ориентацией {110}, как следует из проведенного рассмотрения, возможна инверсия знака ТКЧ при изменении направления намагничивания между касательными осями <111> и <100>.
Экспериментальные результаты
Метод измерения
дисперсионных характеристик ПМСВ был аналогичен использованному в работе [8].
Магнитостатические волны возбуждались и регистрировались с помощью двух пар
микрополосковых преобразователей, изготовленных на металлизированной подложке
из поликора (рис. 6). Исследуемый образец накладывался на модуль и фиксировался
прижимным устройством. С помощью измерителя комплексных коэффициентов передачи
снималась амплитудно-частотная характеристика (АЧХ) модуля. Из-за разницы
расстояний, пройденных МСВ между двумя парами преобразователей, на АЧХ
формировалась интерференционная картина. По интерференционным максимумам и
минимумам определялись значения частоты и волнового числа. В отличие от метода
подвижного преобразователя, позволяющего выбрать любую частоту из спектра МСВ,
в данном методе закон дисперсии строился по дискретному набору значений
волновых чисел и соответствующих им частот. Возможные значения определены интерференционными
равенствами: ![]() и
и ![]() .
.
Измерительная ячейка была расположена между полюсами электромагнита, служившего источником постоянного намагничивающего поля. Изменения температуры образца осуществлялись его охлаждением в парах жидкого азота, либо нагревом с помощью плоского термоэлемента. Для измерения температуры использовалась термопара.
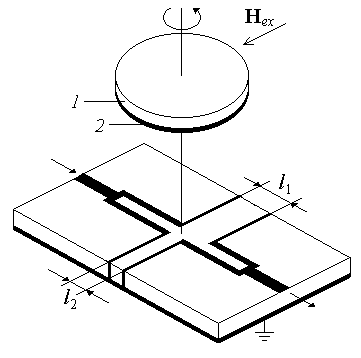
Рис. 6. Конструкция микрополоскового модуля. ![]() . 1 – подложка из кристалла Gd3Ga5O12,
2 – пленка ЖИГ. Изменение кристаллографической ориентации намагничивающего
поля Hex
осуществлялось
поворотом образца.
. 1 – подложка из кристалла Gd3Ga5O12,
2 – пленка ЖИГ. Изменение кристаллографической ориентации намагничивающего
поля Hex
осуществлялось
поворотом образца.
Из
зависимостей ![]() и
и ![]() ,
построенных при температурах
,
построенных при температурах ![]() и
и ![]() , рассчитывался ТКЧ
, рассчитывался ТКЧ

Полученные значения приведены на рис. 7. Для построения расчетных зависимостей были измерены материальные параметры пленки (по методике работы [9]).

Рис.
7. Экспериментальные значения ТКЧ в касательно намагниченной пленке ЖИГ с
ориентацией {110} и толщиной ![]() . Направление
магнитного поля совпадало с касательными осями <100>, <111> и указано
на зависимостях. Напряженность поля
. Направление
магнитного поля совпадало с касательными осями <100>, <111> и указано
на зависимостях. Напряженность поля ![]() . Параметры пленки,
использованные при построении расчетных зависимостей (сплошные кривые):
. Параметры пленки,
использованные при построении расчетных зависимостей (сплошные кривые): ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Экспериментальные результаты подтвердили выводы теории о существенности влияния кристаллографической магнитной анизотропии на температурные характеристики МСВ. Данные на рис. 7 демонстрируют значительную плоскостную анизотропию ТКЧ и термостабилизирующее влияние поля анизотропии для направлений намагничивания вдоль осей типа <100>.
Выводы
1. Выполнен сравнительный анализ температурных характеристик основных типов магнитостатических волн в монокристаллической пленке. При выводе выражений для ТКЧ была учтена температурная зависимость всех параметров, входящих в дисперсионные уравнения. «Привязка» вектора намагниченности к осям симметрии позволила упростить расчеты и выявить физические факторы, определяющие температурные характеристики МСВ. Установлено, что влияние кристаллографической магнитной анизотропии на ТКЧ определяется как температурной зависимостью параметров поля анизотропии, так и ориентацией вектора намагниченности относительно кристаллической решетки и плоскости пленки.
2. Изучены температурные коэффициенты частот ПМСВ в пленке феррита с кубической симметрией кристаллической решетки. Показано, что в пленке с кристаллографической ориентацией типа {110} магнитная анизотропия может приводить к инверсии знака ТКЧ. Основные выводы теории были подтверждены экспериментальным исследованием пленок ЖИГ.
3. Развитые представления могут быть использованы как для обработки результатов физических экспериментов, так и для проектирования пленочных приборов с заданными температурными характеристиками. Из полученных результатов следует, что даже в слабоанизотропных материалах влияние кристаллографической анизотропии на ТКЧ будет существенным. При этом температурными характеристиками МСВ можно управлять, осуществляя выбор кристаллографической ориентации пленки и ориентации намагничивающего поля.
Литература
1. Вашковский А.В., Стальмахов В.С., Шараевский Ю.Г. Магнитостатические волны в электронике СВЧ. Саратов: Изд.-во СГУ, 1993. 316 с.
2. Гласс Х.Л. Ферритовые пленки для СВЧ-устройств // ТИИЭР. 1988. Т. 76, № 2. С. 64-72.
3. Берегов А.С., Кудинов Е.В., Ерещенко И.Н. Улучшение термостабильности устройств на магнитостатических волнах // Электронная техника. Сер. 1. Электроника СВЧ. 1987. Вып. 1(395). С. 19-21.
4. Фетисов Ю.К. Термостабильная ориентация пленки феррита в устройствах на магнитостатических волнах // ЖТФ. 1987. Т. 57, № 12. С. 2393-2397.
5. Луцев Л.В., Березин И.Л. Термостабильность параметров магнитостатических волн, распространяющихся в пленках с произвольным направлением подмагничивания // Электронная техника. Сер. 1. Электроника СВЧ. 1989. Вып. 6(420). С. 3-8.
6. Шагаев В.В. Метод расчета характеристик поверхностных магнитостатических волн в анизотропных ферромагнитных пленках // ЖТФ. 2004. T.74. Вып. 10. С. 108-112.
7. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. – М.: Наука, 1994, 464 с.
8. Гусев Б.Н., Чивилева О.А., Гуревич А.Г., Эмирян Л.М., Наронович О.Б. Затухание поверхностной магнитостатической волны // Письма в ЖТФ. 1983. Т. 9, № 3. С. 159-163.
9. Шагаев В.В. Зависимость частот магнитостатических волн от напряжённости поля подмагничивания в ферритовых плёнках // ФТТ. 1998. Т.40, № 11. С. 2089-2092.

