ПРИМЕНЕНИЕ Модифицированного Метода Дискретных Источников В СФЕРОИДАЛЬНЫХ и тороидальных КООРДИНАТАХ

 А. Г. Кюркчан, С. А. Маненков, Е. С. Негорожина

Московский технический университет Связи и Информатики
 

Получена 28 мая 2013г.

 

Аннотация: Предложен эффективный подход в рамках модифицированного метода дискретных источников к решению трехмерных скалярных задач дифракции волн на сильно вытянутых и сильно сплюснутых осесимметричных частицах, а также на частицах тороидальной формы. Показано, что использование сфероидальных и тороидальных координат более удобно для такого класса задач. Приведен сравнительный анализ использования данных систем координат. Показано, что рассматриваемый метод позволяет существенно сократить объемы вычислений и значительно увеличивает разнообразие геометрий рассеивателей.

Ключевые слова: задача дифракции; модифицированный метод дискретных источников; сферические, сфероидальные, тороидальные координаты.

Abstract: An efficient approach for the modified discrete sources method to the solution of three-dimensional scalar problems of wave diffraction by highly elongated and highly flattened axisymmetric particles, and the particles of the toroidal shape is proposed. It is shown that the use of spheroidal and toroidal coordinates is more convenient for this class of problems. The comparative analysis of these coordinate systems is provided. It’s shown, that the considered method can significantly reduce the amount of computation and greatly increases the variety of geometries of scatterers.

Key words: diffraction problem, a modified method of discrete sources, spherical, spheroidal, toroidal coordinates.

 

Введение

При численном моделировании волновых полей различной физической природы естественным желанием является получение решения с наперёд заданной точностью и с минимальными вычислительными затратами. Существующие в настоящее время численные методы позволяют реализовать только некоторое оптимальное соотношение между получаемой точностью и временем счёта.

Используемый ниже модифицированный метод дискретных источников (ММДИ) [1,2] основан на аналитическом продолжении полей за пределы области их первоначального определения. ММДИ – это обобщённый вариант метода дискретных источников (МДИ) [3], в котором предложен простой и единообразный способ выбора носителя источников, опирающийся на результаты исследований аналитического продолжения дифракционных полей [4,5]. Ниже подробно рассмотрен вопрос о выборе упомянутого носителя. В работах [6,7] предложена модификация ММДИ для расчета векторной задачи дифракции на сильно вытянутых и сильно сплюснутых телах, а также на телах тороидальной формы. В настоящей работе этот подход применен к решению скалярных задач дифракции на телах вращения.

Наличие симметрии вращения позволяет свести задачу к двумерной. Для этого ядро интегрального уравнения раскладывается в ряд Фурье.

Известно, что нахождение коэффициентов Фурье фундаментального решения уравнения Гельмгольца (так называемых S-функций Васильева) представляет собой очень сложную вычислительную задачу. Поэтому в работе сначала ядро раскладывается по вейвлетному базису, и только после этого вычисляются коэффициенты Фурье.

Кроме того, в работе приведен сравнительный анализ решения таких задач в сфероидальных и тороидальных координатах. Показано их преимущество по сравнению с использованием сферических координат.

 

1. Основная идея метода

Для определенности речь будет идти о решении задачи Дирихле для уравнения Гельмгольца. Итак, требуется найти функцию

удовлетворяющую уравнению

всюду вне рассеивателя, занимающего область D с границей S и краевому условию

где  – известная функция (поле падающей на рассеиватель волны), которая имеет вид:

                               .                 (1)

Рассеянное поле удовлетворяет условию на бесконечности

.

Здесь  – сферические координаты.

Рассмотрим реализацию ММДИ в трехмерном случае. В качестве рассеивателя  выберем тело вращения. С использованием представления для поля 

                                                                                   (2)

задача сводится к решению следующего интегрального уравнения:

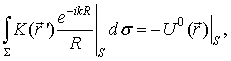                                                    (3)

где – вспомогательный ток, распределенный на замкнутой поверхности ∑, лежащей внутри S, dσ – элемент площади поверхности ∑. Для получения уравнения поверхности ∑ перейдем к сфероидальным координатам (например, вытянутым):

.                       (4)

При этом поверхность вращения задается уравнением . Вспомогательные поверхности определяются соотношениями [6,7]

,                                  (5)

где  – сфероидальные координаты «образа» точки с координатами  на исходной поверхности. Для получения декартовых координат точки на вспомогательной поверхности нужно воспользоваться формулами

       ,                                               (6)

где . В случае сплюснутых сфероидальных координат необходимо взять .

  Рассмотрим также случай тороидальных координат. При этом

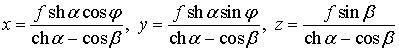          ,                            (7)

 

где  – уравнение поверхности тела в тороидальных координатах. Формулы (5) для определения тороидальных координат точек на вспомогательной поверхности остаются в силе, а для нахождения декартовых координат точек на ∑ следует в формулы (6) подставить величину .

  Таким образом, имеем единообразный подход, позволяющий строить вспомогательные поверхности в различных ортогональных координатах.

   Отметим, что указанная деформация исходной поверхности частицы возможна до тех пор, пока отображение  остается взаимно-однозначным (однолистным). Таким образом, необходимо определить максимальную величину параметра деформации , которая зависит от формы исходной поверхности тела. Ниже приведен численный алгоритм нахождения  для так называемых чебышевских частиц [8].

Разложим далее ядро уравнения (3)  в ряд Фурье:

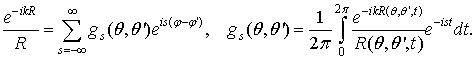                      (8)

Искомый ток также представим рядом Фурье

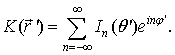                                                                                   (9)

Прямое вычисление коэффициентов , как уже отмечалось, сопряжено с серьезными трудностями. Попытаемся обойти их, представив функцию 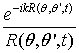 в виде суммы масштабирующей функции и вейвлетов. Например, в случае использования вейвлетов Хаара такое представление будет иметь следующий вид:

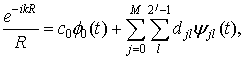                                                (10)

где 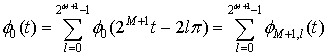– масштабирующая функция, а  – вейвлеты.

 

В соответствии со свойствами кратномасштабного анализа [9,10],

Коэффициенты  в разложении (10) имеют следующий вид:

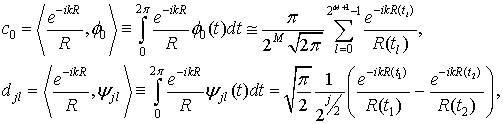
где

Подставив выражение (10) в формулу для  (8), получим:

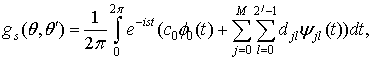
причем

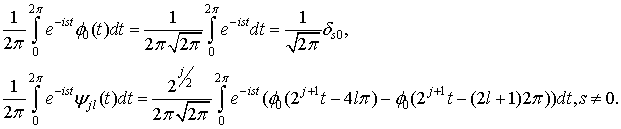
В результате элементы  вычисляются в явном виде, поскольку, например:

 

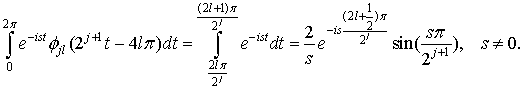
2. Результаты численных исследований

Покажем преимущества сфероидальных координат по сравнению со сферическими. Рассмотрим рассеяние плоской волны на идеально проводящем сфероиде, вытянутом вдоль оси z с большой полуосью . Плоская волна падает вдоль оси вращения тела. В таблице 1 представлены результаты расчета невязки краевого условия при использовании стандартного ММДИ и модификации ММДИ, рассмотренной в настоящей работе. В левой графе показано соотношение полуосей сфероида. Число источников обозначено через N.

Как видно из таблицы, при использовании сфероидальных координат требуется брать количество дискретных источников от 4 до 10 раз меньшее, чем при использовании сферических координат для получения примерно одинакового уровня невязки (чем больше соотношение полуосей, тем значительнее уменьшение размера системы). Таким образом, имеется существенный выигрыш при использовании модификации ММДИ, предложенной в настоящей работе.

 

Таблица 1. Сравнение стандартного ММДИ и модификации ММДИ, использующего сфероидальные координаты.

	Стандартный ММДИ		ММДИ с использованием сфероидальных координат
	N	Максимальный уровень невязки	N	Максимальный уровень невязки
12	700		60
10	500		50
8	350		45
6	200		35
4	100		25

 

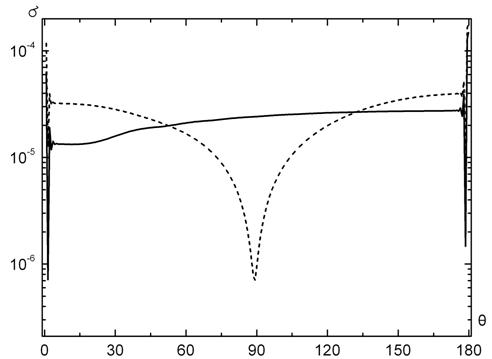
Рис. 1. Зависимость модуля невязки краевого условия от координаты  для сильно вытянутого и сильно сплюснутого сфероида с отношением полуосей 50.

 

На рис. 1 показано распределение модуля невязки краевого условия для вытянутого и сплюснутого идеально проводящего  сфероида с соотношением осей, равным 50. Плоская волна падала вдоль оси вращения тела. Кривые получены с использованием сфероидальных координат. Сплошная кривая на рисунке относится к случаю вытянутого сфероида с полуосями , а штриховая кривая иллюстрирует распределение невязки для случая . Число источников составляло 250. Как видно из рисунка, максимальный уровень невязки не превосходит , то есть достаточно мал. Отметим, что при использовании сферических координат такую точность вычислений получить практически не возможно.

Рассмотрим так называемую частицу Чебышева в сферических координатах

                                       (11)

При  имеем сферу с радиусом . Как указано в [8], уравнение чебышевских частиц в сфероидальных координатах имеет вид:

                           ,                                            (12)

где , причем  – полуоси «невозмущенной» частицы, то есть сфероида, когда параметр ,  – межфокусное расстояние данного сфероида, . Аналогично, тороидальная частица задается в тороидальных координатах в виде (12), причем , где  и  – соответственно, радиус и смещение «невозмущенного» тора (при ). Подчеркнем, что в формуле (12) в различных системах координат смысл величин  и  совершенно различный. Параметр  в (12) не может принимать значения, большие, чем [6,7]

,                                           (13)

так как в противном случае контур осевого сечения частицы имел бы точки самопересечения.

Сделаем пояснение относительно выбора вспомогательных поверхностей для чебышевской и тороидальной частицы. Рассмотрим этот вопрос на примере чебышевской частицы. Предполагаем, что контур осевого сечения частицы не имеет самопересечений. Для определения максимальной степени деформации, то есть параметра , необходимого для построения вспомогательной поверхности, мы использовали алгоритм, аналогичный методу половинного деления при решении нелинейных уравнений. Вначале задаем некоторое значение , при котором контур осевого сечения вспомогательной поверхности имеет самопересечения, причем последнее эквивалентно тому, что

                                                                                                   (14)

для некоторого  из интервала . Далее рассматриваем интервал  изменения параметра . Делим этот интервал пополам и проверяем, выполняется ли условие (14) для значения  из середины исходного интервала. При этом функция  строится так, как было описано выше. Если указанное условие выполняется, то берем левую половину интервала , если нет, то правую, и вновь делим ее пополам, и т. д. Алгоритм заканчивает работу при условии, что длина интервалов, на которые разбит исходный интервал , будет меньше заданной малой величины. В результате за  принимаем левую границу интервала, рассматриваемого на последней итерации. Существенно отметить, что данный алгоритм построения вспомогательной поверхности согласуется с результатами работы [11], в которой показано, что для корректности использования метода необходимо, чтобы внутренняя вспомогательная поверхность охватывала особенности аналитического продолжения внешнего поля внутрь частицы.

Уравнение данных особенностей для сфероидальных и тороидальных частиц имеет вид:

                                               ,                                                  (15)

где штрих означает производную по переменной . Особые точки в осевом сечении для фигур рассматриваемого вида являются точками ветвления алгебраического характера [4], поэтому они должны быть соединены разрезами. Геометрия этих разрезов и определяет упомянутые выше области однолистности. Для вытянутых чебышевских частиц, по крайней мере, один из разрезов идет вдоль оси , что и приводит к условию (14). Для тороидальных частиц разрез проходит по линии . Как показывают расчеты, самопересечение вспомогательной поверхности, определяемое с помощью условия (14), происходит «раньше» пересечения вспомогательной поверхностью особенностей аналитического продолжения поля.

Рассмотрим результаты расчета диаграмм рассеяния чебышевских и тороидальных частиц. Диаграмму рассеяния вычисляем с использованием ММДИ в сферических и в сфероидальных координатах. Сначала рассмотрим чебышевскую частицу с размерами:  (см. рис. 2). Для построения диаграмм размер алгебраической системы был равен N=180. Невязка граничного условия в сферических координатах принимает значение порядка , а в случае сфероидальных меньше, чем  (см. рис. 3). Далее, будем уменьшать малую полуось. В результате уже при kb=10 (см. рис. 4), в случае сферических координат диаграмма рассеяния весьма существенно отличается от диаграммы, полученной в сфероидальных. При этом точность вычислений во втором случае не изменяется. Это свидетельствует о целесообразности применения сфероидальных координат. При kb=5 в сферических координатах при выбранном значении N не удается получить сколько-нибудь достоверный результат. В то же время в сфероидальных координатах удается вычислить диаграмму для частицы размером ka=20, kb=2 и ka=30, kb=2, с приемлемой точностью.

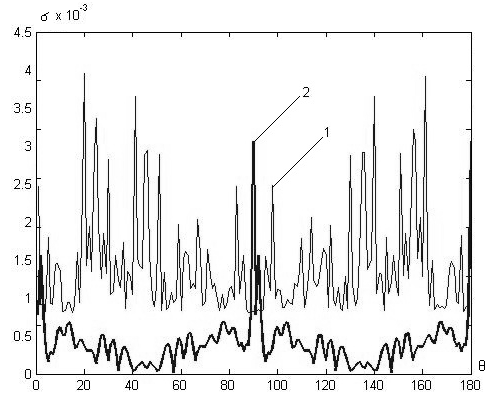
На рис. 5 приведены зависимости модуля невязки краевого условия для тороидальной частицы с параметрами: . По оси абсцисс отложена координата . Волна падает перпендикулярно оси частицы. Кривая 1 соответствует числу источников, равному , кривая 2 – , кривая 3 – . Как видно, уже при  уровень невяки не превосходит . При этом, как видно из врезки к рисунку 6, частица является сильно «изрезанной». Таким образом, имеем хорошую точность вычислений для сильно деформированной тороидальной частицы.

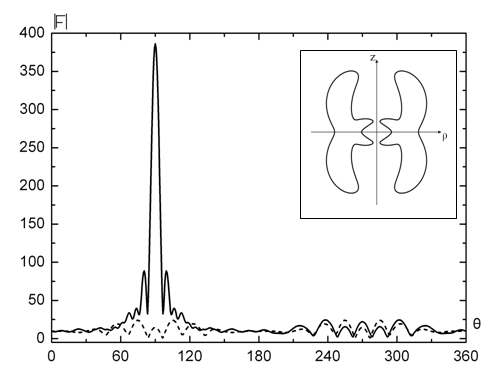
На рис. 6 показана диаграмма рассеяния от угла  для тороидальной частицы с параметрами, указанными выше. Волна падала под углом . Диаграмма построена для углов наблюдения (сплошная кривая) и  (штриховая кривая).

 

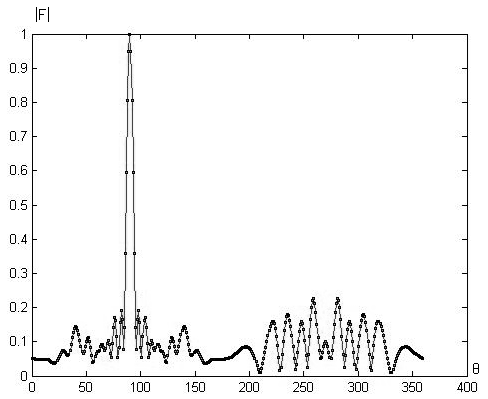
Рис.2. Диаграмма рассеяния волны, падающей на частицу размеров  ,сплошная линия-сфероидальные координаты, точки-сферические координаты.

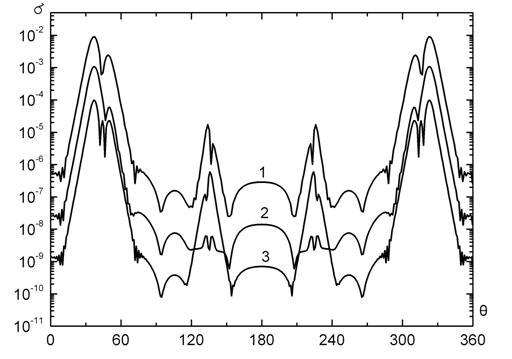
Рис.3. Невязка краевого условия в задаче дифракции на частице Чебышева сферические координаты (кривая 1), сфероидальные координаты (кривая 2).

Рис.4. Диаграмма рассеяния волны, падающей на частицу размеров , сферические координаты (кривая 1), сфероидальные координаты (кривая 2).

 

Рис.5. Зависимость модуля невязки краевого условия для тороидальной частицы с параметрами ka=10, kb=15, .

 

Рис.6. Диаграмма рассеяния волны, падающей на тороидальную частицу с параметрами ka=10, kb=15, .

 

3. Выводы

Проведено исследование эффективности ММДИ при решении скалярных задач дифракции в различных системах координат. Установлена целесообразность применения сфероидальных и тороидальных координат. Численные расчеты показали, что предложенный подход позволяет решать задачи дифракции волн на телах весьма сложной геометрии с высокой точностью при относительно небольших объемах вычислений.

 

Литература

1.     Кюркчан А.Г., Минаев С.А., Соловейчик А.Л. Модификация метода дискретных источников на основе априорной информации об особенностях дифракционного поля. Радиотехника и электроника. 2001. Т. 46. №6 С. 666 – 672.

2.     Алексидзе М.А., Фундаментальные функции в приближённых решениях граничных задач, М., Наука, 1991.

3.     Anioutine A.P., Kyurkchan A.G., Minaev S.A. About a universal modification to the method of discrete sources and its application. Journal of Quantitative Spectroscopy & Radiative  Transfer, 79-80 (2003) 509-520.

4.     Апельцин В.Ф., Кюркчан А.Г., Аналитические свойства волновых полей. МГУ 1990 г.

5.     Кюркчан А.Г., Стернин Б.Ю., Шаталов В.Е. Особенности про-должения волновых полей. УФН, т. 166, N12, 1996. С. 1285 – 1308.

6.     Kyurkchan A.G., Manenkov S.A. Application of different orthogonal coordinates using modified method of discrete sources for solving a problem of wave diffraction on a body of revolution. Journal of Quantitative Spectroscopy & Radiative  Transfer, 113 (2012) 2368-2378.

7.     Кюркчан А.Г., Маненков С.А. Применение различных ортогональных систем координат для моделирования рассеяния волн группой тел. Радиотехника и электроника. 2012. Т. 57. №9 С. 987 – 995.

8.     Фарафонов В.Г., Винокуров А.А., Барканов С.В. Электростатическое решение и приближение Рэлея для малых несферических частиц в сфероидальном базисе. Оптика и спектр. 2011. Т.111.  №5. С.852-865.

9.     Блаттер К. Вейвлет-анализ. Основы теории. М.: Техносфера, 2004.

10.Чуи К. Введение в вэйвлеты. М.: Мир, 2001.

11.  Кюркчан А.Г., Смирнова Н.И. Методы вспомогательных токов и нулевого поля. Электромагнитные волны и электронные системы. 2009. Т. 14. №8. С. 4 - 12.