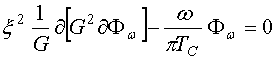УДК 538.945; 530.145

СВЕРХПРОВОДЯЩИЕ φ-ЭЛЕМЕНТЫ НА ОСНОВЕ ДЖОЗЕФСОНОВСКИХ СТРУКТУР С ФЕРРОМАГНИТНЫМИ СЛОЯМИ

 

Н. В. Кленов^1,2, С. В. Бакурский^1,2, В. И. Ружицкий², А. В. Кузнецов², К. Е. Нестеров², С. Ж. Герасимова²,  И. И. Соловьев¹

¹ Московский государственный университет имени М.В. Ломоносова, НИИЯФ

² Московский государственный университет имени М.В. Ломоносова, Физический факультет
 

Получена 20 мая 2013 г.

 

Аннотация.  В статье изложены основы моделирования транспорта тока через джозефсоновские гетероструктуры с нормальным и ферромагнитным би-каналом слабой связи произвольной геометрии и анализа ток-фазовых зависимостей. Предложен метод создания на основе джозефсоновских структур с NF би-каналом не только джозефсоновских φ-контактов, но и перспективных φ-ячеек со встроенным заданием рабочей точки, представлен анализ параметров таких элементарных логических ячеек, содержащих φ-контакты.

Ключевые слова: эффект Джозефсона, магнитный джозефсоновский переход, ток-фазовая зависимость.

Abstract: The article describes the basics of both: the modeling of current transport through the Josephson heterostructures with ferromagnetic and normal bi-channel as weak link of arbitrary topology and the analysis of its current-phase relation. We propose a method to create φ-contacts on the base of such Josephson heterostructures with NF bi-channel and to realize promising φ-cells with built-in frustration. We analyze the parameters of such elementary cells containing φ-contacts.

Key words: Josephson effect, magnetic Josephson junction, current-phase relation.

 

Введение

Развитие твердотельной сверхпроводниковой электроники, позволяющей создавать устройства с чрезвычайно высоким быстродействием (характерная частота F_c которых лежит в диапазоне от десятков до сотен гигагерц) и низким энерговыделением [1] (характерная энергия переключения сверхпроводникового джозефсоновского логического элемента между состояниями составляет порядка E_J = 2∙10^-15 Вб · 10^-4 А ≈ 10^-18 Дж), требует все более и более глубокого изучения особенностей основы её элементной базы – джозефсоновского контакта. Джозефсоновский контакт представляет собой слабую связь (например, изолирующую прослойку или область нормального металла) между двумя сверхпроводниками, через которую может течь бездиссипативный сверхток, величина которого зависит от разности фаз φ комплексного параметра порядка на разных берегах сверхпроводника [2].

В последние годы проблема создания сверхпроводниковой магнитной памяти и спиновых вентилей сформировала устойчивый интерес к джозефсоновским структурам с ферромагнитными слоями. В таких гетероструктурах сосуществование столь различных явлений, как сверхпроводимость и ферромагнетизм, приводят к осцилляциям критического тока как функции толщины ферромагнитной прослойки, используемой в качестве слабой связи, что открывает путь к реализации джозефсоновских π-контактов – контактов с джозефсоновской фазой φ₀ = π в основном состоянии в отсутствие тока, т.е. отрицательным критическим током I_C. Использование уже созданных π-контактов с большим критическим током для сдвига фазы на π (фазовых π-инверторов) может существенно уменьшить размеры логических элементов и увеличить скорость работы интегральных схем быстрой одноквантовой логики [3-5].

В настоящее время активно изучаются сложные гетероструктуры, в том числе с нормальными (N) и ферромагнитными (F) слоями, граница между которыми расположена вдоль направления протекания тока. Ожидается, что использование таких структур позволит не только улучшить характеристики существующих элементов и схем, но и создать новые устройства, включая высокоэффективные спиновые вентили [6,7].

Для работ по совершенствованию сверхпроводниковых квантовых битов важным шагом вперед стало бы создание φ-контактов на основе SFS структур  – контактов, основным устойчивым состоянием которых в отсутствие тока через слабую связь (J_S = 0) становится состояние с отличной от нуля разностью фаз φ₀, то есть J_S(φ₀) = 0, φ₀ ≠ 0, πn (n – целое число). Для развития современных квантовых вычислений появление φ-контактов означало бы уменьшение размеров сверхпроводящих квантовых битов, низкую индуктивность и слабую чувствительность к внешним шумам [8-10]. При этом немалый интерес, на наш взгляд, может представлять использование φ-контактов как компактных фазовых батарей в сверхпроводящих логических элементах, работающих по «классическим» законам.

Цель настоящей работы – изложение подходов к моделированию токового транспорта в общем случае джозефсоновских гетероструктурах с N и F би-каналом в области слабой связи и оптимизации свойств таких структур в зависимости от их конкретной топологии для включения в устройства сверхпроводниковой электроники. Особое внимание уделено исследованию эффекта близости: проникновению куперовских пар – носителей сверхтока – из сверхпроводника в N и F слои области слабой связи.

2. Модель

Для описания сверхпроводящих систем в грязном пределе, когда длина свободного пробега электрона l_e много меньше и длины когерентности ξ, и характерного геометрического размера структуры, используется система уравнений Узаделя [11,12] для нормального и сверхпроводящего слоев соответственно:

,                           (1)

                           (2)

 

где G и Ф – нормальная и аномальная функции Грина, характеризующие плотность квазичастиц и куперовских пар соответственно, Δ – потенциал спаривания,  – мацубаровская частота, ξ – длина когерентности в материале, зависящая от критической температуры T_C и коэффициента диффузии D.

Учет магнитных свойств вещества в рамках уравнения Узаделя также возможен. В распространенном частном случае магнитные свойства характеризуются энергией обменного (среднего) поля H в материале. Обменное поле изменяет эффективную энергию электронов в среде, что может быть описано заменой мацубаровской частоты  на эффективную частоту . Это приводит к появлению асимметричности уравнений по номеру мацубаровской частоты и увеличению размерности уравнений. Уравнение Узаделя для ферромагнетика принимает вид.

                                                     (3)

 

Границы между системами сверхпроводников, нормальных металлов, ферромагнетиков и изолятором описываются с помощью условий Куприянова-Лукичева [13]. В общем случае двух материалов с эффективными мацубаровскими частотами  и  они записываются в виде:

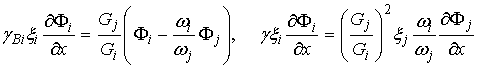         , (4)

где

,   – 

 

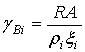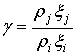безразмерные параметры границы, R  –  сопротивление контакта, A – его площадь, i,j  –  обозначения материалов по разные стороны от неё; ρ_i  –  удельное сопротивление этих материалов. Здесь достаточно задать только первое граничное условие и характеристики материалов, так как второе является его следствием. Действительно, из

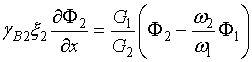                                                       (5а)

                                                         (5б)

 

прямым образом вытекает уравнение (4). В такой форме (5а-5б) граничные условия и будут записываться дальше.

Для моделирования токового транспорта через структуры с произвольной геометрией необходимо записать граничные условия на всех границах между различными материалами. Сделаем это для относительно простой структуры с FN бислоем в области слабой связи между S-электродами (см. рисунок 1а), позволяющей, как было показано, при определенных условиях создать φ-контакт.

 

Рис. 1. Схематичное изображение топологий (а) S-FN-S и   (б)  SN-FN-NS структур.

Здесь d_N и d_F – толщины слоев соответственно нормального металла и ферромагнетика; W – ширина слоев (размер вдоль оси, перпендикулярной плоскостям рисунков), причем мы полагали, что распределение тока по ширине однородно. Длина би-канала L (расстояние между S-электродами) в рамках рассматриваемого подхода к теоретическому анализу может меняться  в широких пределах.

Связь между ферромагнитной и нормальной прослойками в такой S-FN-S структуре опишем через граничные условия на FN границе:

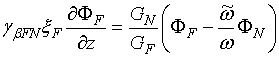                                                  (6а)

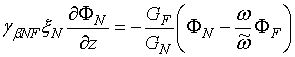                               ,               (6б)

где  -

 

параметр, характеризующий слой изолятора между слоями.

 

В рамках рассматриваемой модели мы пренебрегаем подавлением потенциала спаривания Δ в сверхпроводнике, что позволяет решать задачу о расчете функций Грина только внутри нормально-ферромагнитного бислоя с жестко заданными граничными условиями. Это приближение применимо в случае значительных толщин диэлектрика на границе с ним, однако, даже если это условие не выполнено, характеристики зарядового транспорта в этом случае качественно не изменятся, и полученные результаты можно будет использовать с  некоторой количественной поправкой. Таким образом, можно записать жесткие граничные условия на границах SN, SF:

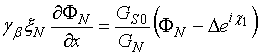                               ;                      (7а)

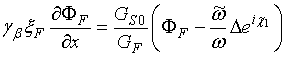                                                 (7б)

На границах NS, NF:

 ,                  (8а)

,              (8б)

где

,   – 

 

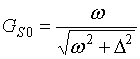функции Грина однородного сверхпроводника, , –  фазы потенциала спаривания в электродах.

Остаются поверхности, на которых би-канал ограничен массивным изолятором (NI, FI). Здесь граничное условие принимает совсем простой вид:

                            ,       .                                       (9)

 

Таким образом, система уравнений оказывается замкнутой, и для полного описания системы достаточно решить двухмерную краевую задачу с граничными условиями третьего рода.

 

3. Алгоритм расчета характеристик джозефсоновской структуры, включающей слои нормального металла и ферромагнетика в области слабой связи

Основной сложностью при моделировании подобных систем является нелинейность уравнения Узаделя (1), (2). Для численного решения таких уравнений используются итерационные методы, в которых производится линеаризация относительно , а потом уже используются стандартные методы решения линейных систем, таких как метод Гаусса или n-диагональной прогонки. Встает вопрос в способе линеаризации. В настоящей работе линейность базовой системы достигается следующим образом. Вводится дополнительная затравочная функция  и задается ее начальное значение. При каждом вычислении матрицы  гриновская функция считается заранее заданной, после чего по вычисленным значениям производится расчет новой . Подобные итерации проводятся до тех пор, пока изменение нормальной функции за один шаг не окажется меньше малой величины .

Итак, базовая структура разработанного численного метода:

А) Задаем параметры системы, создаем сетку размером  для значений функций , и заполняем её затравочными значениями массива .

Б) Начинаем цикл суммирования по мацубаровским частотам . Все дальнейшие вычисления проходят для фиксированной .

В1) Решаем двухмерную краевую задачу. Для составления системы уравнений используется численная схема типа крест, полученная из уравнения Узаделя:

            

Для замкнутости дополняем систему граничными условиями, также записанными в разностном виде. Полученная система линейных уравнений размерности решается с помощью специального метода Гаусса для -диагональных матриц.

В2) Необходимо сразу решить такую же задачу для отрицательной мацубаровской частоты . Это возможно благодаря тому, что нормальные гриновские функции для противоположных частот прямым образом связаны друг с другом. Действительно,

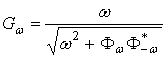                                    .                                    (10а)

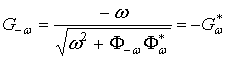                                .                           (10б)

 

Тогда нужно заново решить систему равнений для частоты и матрицы .

Г) По результатам пунктов В1 и В2 строим новую матрицу

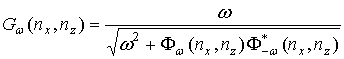                        .              (11)

 

Если в каждой точке  только что построенная функция отличается от старой меньше чем на заданную величину , то можно считать алгоритм сошедшимся и по полученным (x,y) и (x,y) анализировать характеристики системы. Иначе нужно вернуться в пункт В) и повторить вычисления.

Д) Имея функции Грина, являющиеся решением краевой задачи, вычисляем ток через структуру. Общее выражение для джозефсоновского тока имеет вид:

 

, (12)

 

где T – температура, W – толщина прослойки, φ – фаза джозефсоновского перехода, индекс i – тип материала. Вычисляя такой ток при джозефсоновских фазах от 0 до 2, можно получить ток-фазовую зависимость и, определив максимум этой функции, узнать критический ток перехода. Наиболее информативными оказываются значения гармоник ток-фазовой зависимости  (ТФЗ), которые получаются после преобразований Фурье:

 

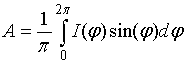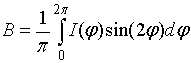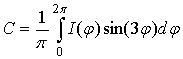;;. (13)

 

Также это позволяет проверить отсутствие четных по фазе φ компонент в разложении ток-фазовой зависимости, предсказанное теоретически и многократно проверенное экспериментально.

Наконец, при необходимости можно рассчитать также и распределение тока по структуре. В этом случае компоненты тока имеют вид:

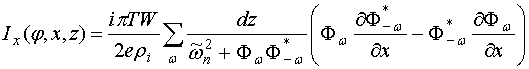.       (14а)

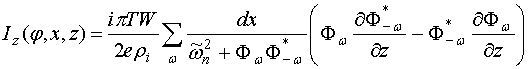        (14б)

 

4. φ-контакт на основе джозефсоновских гетероструктур с NF биканалом

Численное решение двумерной задачи на функции Грина Ф и G в NF би-слое дает возможность рассчитать джозефсоновский ток через изучаемую структуру, используя (для случая S-FN-S перехода) выражение:

;        

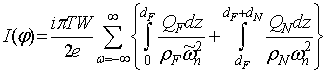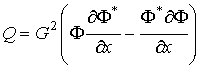
В отличие от работ [14,15], оперирующих с линеаризованным уравнением Узаделя, используемый подход позволяет вычислять не только критический ток, но и ток-фазовые зависимости вида (оставляем далее только две первые гармонические компоненты)

I_S(φ) = A sin(φ) + B sin(2φ ) +…                         (15)

как для компонент тока через нормальную и ферромагнитную прослойки I_N  и I_F , так и для перехода в целом.  Уже было показано, что при соизмеримости вкладов в общий джозефсоновский ток нормальной и ферромагнитной компонент в определенном диапазоне параметров гетероструктуры возможно формирование φ-контакта [16,17]. Для существования такого состояния необходимо выполнение двух следующих условий:

| B | > |A|/2 ,                                               (16а)

B < 0.                                                       (16б)

Отметим, что в случае, когда вторая гармоника в ТФЗ вида (15) достаточно велика, но положительна, устойчивые бестоковые состояния будут существовать либо при φ₀ = 0, либо при φ₀ = π  (0-π контакты). Достаточно большая амплитуда второй гармоники (| B | > |A|/2) и для φ-, и для 0-π контактов приводит к специфическим динамическим характеристикам джозефсоновской системы: так, на рис. 2б показано, что уже в рамках простейшей резистивной модели вид генерации на φ-контакте меняется настолько сильно, что может, например, спровоцировать «лишние» срабатывания сверхпроводникового логического элемента. Это заставляет обращать особое внимание на вид ТФЗ принципиально новых джозефсоновских переходов (разрабатываемых, в том числе для ячеек быстрой магнитной джозефсоновской памяти) [18].

 

 

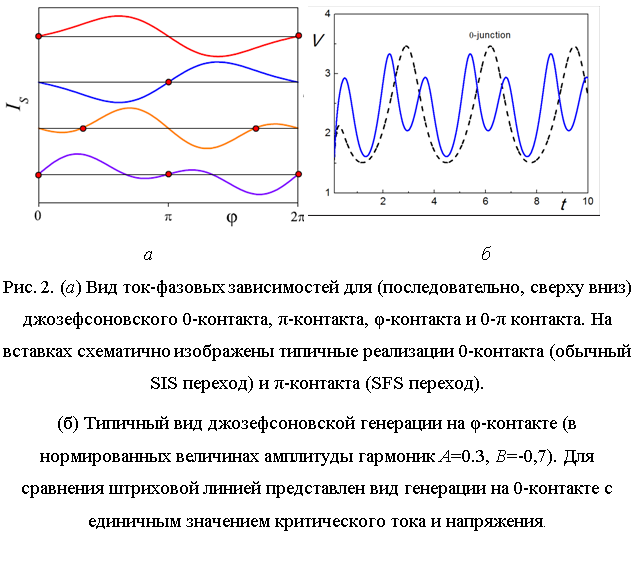
          С другой стороны, компактные φ-контакты вполне могут найти свое применение в сверхпроводниковой электронике:

-при реализации перестраиваемых источников джозефсоновской фазы на чипе [19],

- при создании защищенных квантовых систем обработки информации [8-10],

- для сверхпроводниковых перестраиваемых метаматериалов с генерацией второй гармоники [20].

В обычных SNS переходах типа «сэндвич» условие (16б) на знак второй гармоники выполняется, но условие (16а) не выполняется, так как величина второй гармоники мала при всех разумных температурах (T > 0,1T_C). В SFS сэндвичах условие (16а) на соотношение амплитуд выполняется в области смены знака амплитуды первой гармоники, однако в этой области вторая гармоника всегда положительна, то есть, не выполняется условие (16б). В случае гетероструктур с FN би-каналом оба условия могут быть одновременно выполнены в области смены знака амплитуды первой гармоники [17]. На рис. 3 сплошной и штриховой линиями представлено поведение соответственно амплитуд первой (A) и второй (B) гармонических компонент ТФЗ перехода, а также его нормальной и ферромагнитной компонент. К сожалению, как и во всех джозефсоновских структурах с магнитной прослойкой, попасть в эксперименте в область смены знака первой гармоники не слишком просто. Однако и тут использование сложной прослойки позволяет увеличить устойчивость к разбросу параметров в несколько раз. Действительно, если
 

 

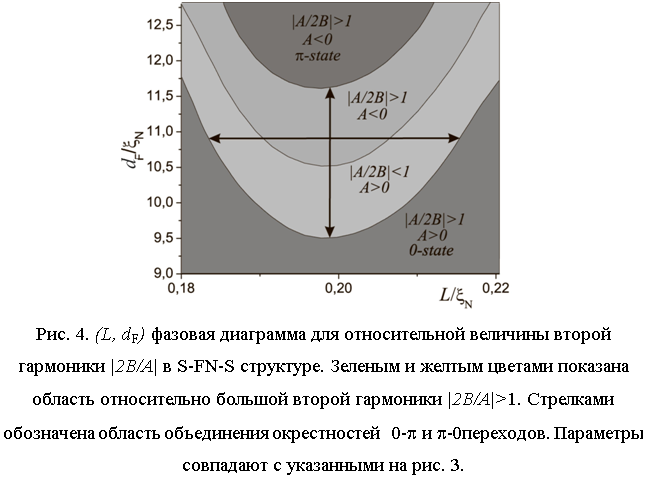
изменение знака первой гармоники происходит в точке, где токи через нормальный металл и ферромагнетик равны по модулю и противоположны по направлению, то это приводит к объединению окрестностей 0-π и π-0 переходов в одну большую область. Фазовая плоскость, позволяющая составить представление о требованиях на допустимый разброс параметров изготовления гетероструктур, представлена на рис. 4. Хотелось бы отметить, что представленная на рис. 1а топология S-FN-S структуры с технологической точки  зрения выгодно отличается от варианта, обсуждавшегося в работе [17].

 

Все интересные свойства, обнаруженные для показанной на рис 1а структуры, могут быть реализованы в SN-FN-NS структуре, которая изображена на рис. 1б. Это достигается за счет того, что имеет место прямой контакт N канала с S-электродами, причем эффективная длина этого канала близка к длине F канала. В качестве примера на рис. 5 показана зависимость амплитуд первой и второй гармоник полного тока, а также токов I_N  и I_F, для случая малого влияния эффекта близости на NF границе (осцилляции тока I_N отсутствуют). На основе такой структуры также возможно формирование φ-контакта – контакта, основным устойчивым состоянием которого в отсутствие тока через слабую связь является состояние с отличной от нуля джозефсоновской фазой.

 

 

Поскольку период осцилляций критического тока и амплитуд гармоник ТФЗ с увеличением длины L может быть сделан достаточно большим для структур с FN би-каналом, диапазон ΔL, в котором выполняются условия (16), также может быть достаточной величины, при которой делается возможным воспроизводимое формирование φ-контактов. Это подтверждают следующие оценки. При использовании меди с длиной когерентности ξ_N = 100 нм в качестве нормальной прослойки (удельное сопротивление ρ_N= 5∙10^-8 Ом∙м) в качестве материала для F-канала можно взять сильно разбавленный ферромагнетик с длиной когерентности порядка ξ_F ~10 нм. В качестве такого слабого ферромагнетика можно использовать, например, сплав Pd_0.99Fe_0.01 с температурой Кюри для тонких пленок порядка 10 К [21-23]. Сверхпроводящие электроды в первых экспериментальных реализациях гетероструктур с NF би-слоями были сформированы из алюминия с характерной критической температурой T_C = 1,21 K [21]. Подстановка перечисленных величин в результаты численных расчетов позволяет оценить размеры структуры, на которых возможна реализация φ-контакта, а также допустимый диапазон их отклонений: расстояние между S-электродами L ~ 60 нм ± 3нм, толщина ферромагнетика d_F ~ 200 нм ± 20 нм, толщина нормального металла d_N > 100 нм. Положив ширину перехода W=140 нм, получим, что для φ-контакта критический ток примерно равен ~3 мкА. Таким образом, и размеры структуры, и та точность, с которой эти размеры необходимо выдерживать, оказываются вполне доступными для современной технологии [21].

 

5. Спонтанные токи в ячейках с φ-контактами

 

 

 

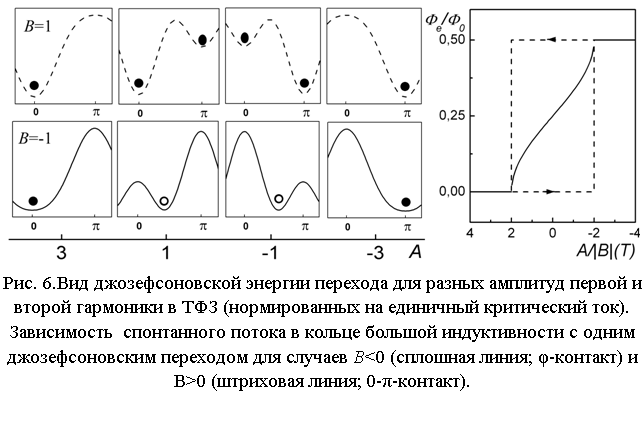
Отдельной важной проблемой является исследование спонтанных токов, возникающих в ячейках с φ-контактами. Как утверждалось выше, при малых амплитудах первой гармоники |A|<2|B| и отрицательной второй B<0 на потенциальной энергии

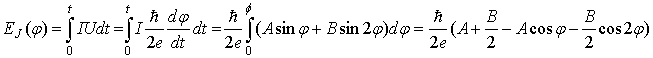
формируется минимум в нетривиальной точке 0<|φ|<π. В противоположном случае B>0, формируется две потенциальные ямы в точках 0 и π, глубины которых изменяются в зависимости от отношения A/|B|. Качественно поведение джозефсоновской энергии перехода проиллюстрировано на рис. 6. Создав структуру с относительно малой первой гармоникой и сделав ее частью сверхпроводящего кольца (одноконтактного интерферометра), можно измерить зависимость спонтанного магнитного потока через сквид в зависимости от температуры Ф(T), по аналогии с тем, как это было сделано при исследовании спонтанных токов в структурах, содержащих джозефсоновские π-контакты [24]. При изменении температуры структура претерпевает переход из 0 в π состояние, в котором поток изменяется от нуля до половины кванта магнитного потока Ф₀/2  (в π-состоянии). Если вторая гармоника меньше нуля, то при каждой температуре будет формироваться своя устойчивая фаза перехода, а значит изменение Ф(T) должно быть плавным и непрерывным. Напротив, если мы включили в кольцо джозефсоновский 0-π контакт, изменение заключенного в кольце потока будет происходить резким скачком, а сама зависимость окажется гистерезисной.

 

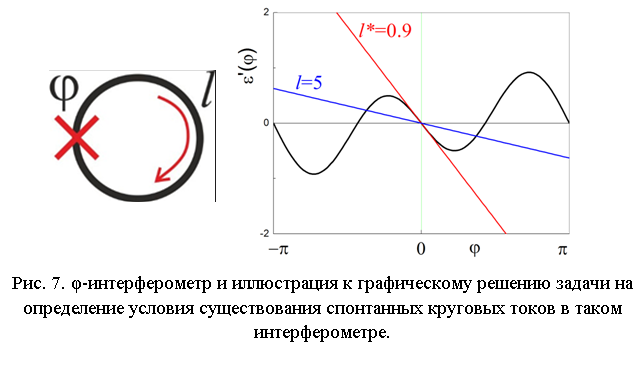
         Отметим, что при включении φ-контакта в сверхпроводящее кольцо конечной индуктивности спонтанный круговой ток и связанный с ним магнитный поток могут и не возникнуть: все зависит от соотношения между характерными значениями джозефсоновской и индуктивной энергий в системе [25].  Нормированная энергия интерферометра и необходимое условие экстремума имеют вид:

 

,                       (17)

 

 

 

Отсюда очевидно, что минимум потенциальной энергии при φ₀ ≠ 0, возможен, как показано на рис. 7, только если нормированная индуктивность сверхпроводящего кольца l = L/L_J > l*=0.9  (джозефсоновская индуктивность перехода  L_J = F₀/2pI_C, I_C – критический ток джозефсоновского перехода).

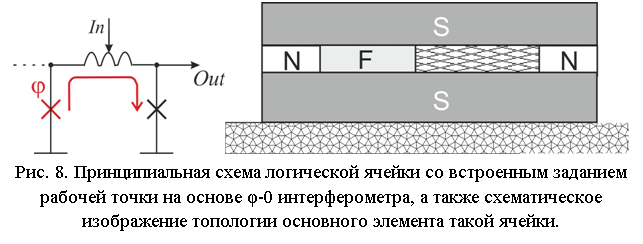
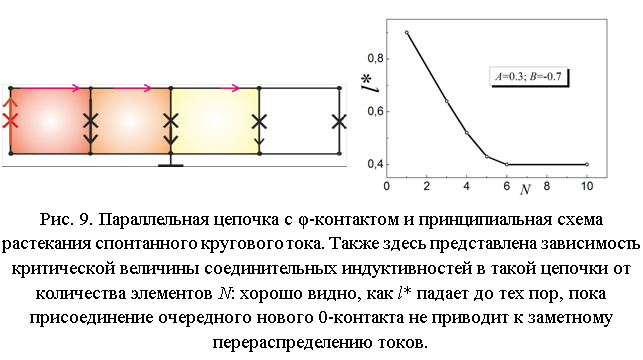
Добавив в кольцо φ-интерферометра обычный джозефсоновский 0-контакт можно получить φ-ячейку со встроенной асимметрией, представленную на рис. 8 (там же представлено схематическое изображение топологии, позволяющей реализовать 0-φ интерферометр на базе джозефсоновских переходов с NF би-каналом в области слабой связи). Очевидно, что дополнительно включая в кольцо φ-интерферометра  0-контакт(ы) мы вносим в систему дополнительные линейные и нелинейные индуктивности, что позволяет (одновременно с улучшением функционала устройства) уменьшить требования на нормированную минимальную соединительную индуктивность. Для примера, в параллельной цепочке из N джозефсоновских переходов, содержащей один φ-контакт и (N-1) 0-контакто критическая величина одной соединительной индуктивности будет падать с ростом N как показано на рис. 9, до тех пора, пока не выйдет на насыщение при N>6.

6. Выводы

Изложены основы численного моделирования двумерного токового транспорта через джозефсоновские гетероструктуры с нормальным и ферромагнитным би-каналом слабой связи и представлены результаты анализа ток-фазовых зависимостей. Рассмотрены топологии таких структур NF биканалом, открывающие возможности для реализации φ-контактов, использование которых позволит существенно оптимизировать конструкцию потоковых квантовых битов и существенно уменьшить чувствительность к флуктуациям прикладываемых к ним магнитных полей, увеличивая тем самым время потери когерентности. Исследованы условия возникновения спонтанных токов в системах с φ-контактами, на основе которых могут быть созданы логические элементы со встроенным заданием рабочей точки.

 

Работа выполнена при поддержке Министерства образования и науки РФ (ГК 14.513.11.0009, Соглашение 8746), стипендии Президента РФ. Авторы крайне признательны Куприянову М.Ю. за помощь в создании численных алгоритмов и участие в обсуждение полученных результатов.

Литература

1.     Mukhanov O.A. Energy-Efficient Single Flux Quantum Technology // IEEE Transactions on Applied Superconductivity, 2011. V. 21, 3. P. 760 – 769.

2.     Golubov A.A., Kupriyanov M. Yu., Il'ichev E. // Rev. Mod. Phys., 2004. V. 76.         P. 411.

3.     Feofanov A. K., Oboznov V. A., Bol’ginov V. V., Lisenfeld J., Poletto S.,  Ryazanov V. V., Rossolenko A. N., Khabipov M., Balashov D., Zorin A. B., Dmitriev P. N., Koshelets V. P., Ustinov A. V. // Nature Physics, 2010. V. 6. P. 593.

4.     Ustinov A. V., Kaplunenko V. K., // J. Appl. Phys., 2003. V. 94. P. 5405.

5.     Wetzstein O., Ortlepp T., Stolz R., Kunert J., Meyer H.-G., Toepfer, H. // IEEE Transactions on Applied Superconductivity, 2011. V. 21. P. 814 – 817.

6.     Fominov Ya.V., Golubov A.A., Karminskaya T.Yu., Kupriyanov M.Yu., Deminov R.G., Tagirov L.R. // JETP Letters, 2010. V. 91. P. 329-333.

7.     Tagirov L.R. // Phys. Rev. Letters, 1999. V. 83. No 10. P. 258-261.

8.          Van der Waal C. H. , ter Haar A. C. J., Wilhelm F. K., Schouten R. N., Harmans C. J. P. M., Orlando T. P., Seth Lloyd, Mooij J. E. // Science, 2000. V. 290. P. 773-776.

9.     Amin M. H. S., Smirnov A. Yu., Zagoskin A. M., Lindstrom T., Charlebois S. A., Claeson T., Tzalenchuk A. Ya.// Phys. Rev. B, 2005. V. 73. P. 064516-1-5,

10.           Klenov N. V., Kornev V. K., Pedersen N. F. // Physica C, 2006. V. 435. P. 114-117.

11.           Usadel K.D. Generalized Diffusion Equation for Superconducting        Alloys // Phys. Rev. Lett., 1970. V. 25. P. 507.

12.           F. S. Bergeret, A. F. Volkov, and K. B. Efetov // Rev. Mod. Phys., 2005. V. 77. P. 1321.

13.           M.Yu. Kuprianov, V. F. Lukichev // Zh. Eksp. Teor. Fiz., 1998. V. 94. P. 139.

14.            Karminskaya T.Yu., Golubov A.A., Kupriyanov M.Yu., Sidorenko A.S. // Phys. Rev. B, 2009. V.79. No.13. P. 134516.

15.           Karminskaya T.Yu., Golubov A.A., Kupriyanov M.Yu., and Sidorenko A.S. // Phys. Rev. B, 2010. V. 81. P. 214518.

16.           Кленов Н. В., Пугач Н. Г., Шарафиев А. В., Бакурский С. В., Корнев В. К. // Физика Твердого Тела, 2010. Т. 52. С. 2104-2109.

17.           Bakurskiy S. V., Klenov N. V., Karminskaya T. Yu., Kupriyanov M. Yu. and Golubov A. A. // Superconductor Science and Technology, 2013. V. 26. P. 015005.

18.           Vernik I.V., Bol’ginov V. V., Bakurskiy S. V., Golubov A.A., Kupriyanov M. Yu., Ryazanov V. V., Mukhanov O. A. Magnetic josephson junctions with superconducting interlayer for cryogenic memory // IEEE Transactions on Applied Superconductivity, 2013. V. 23. P. 1701208.

19.           Pugach N. G., Goldobin E., Kleiner R., Koelle D.  Method for reliable realization of a φ Josephson Junction // Phys. Rev. B, 2010.V. 81. P. 104513.

20.            S. Savel'ev, V.A. Yampol'skii, A.L. Rakhmanov, F. Nori // Phys. Rev. B, 2005.V. 72. P. 144515.

21.           Golikova T. E., Hubler F., Beckmann D., Batov I. E., Karminskaya T. Y., Kupriyanov M. Y., Golubov A. A. and Ryazanov V. V. // Phys. Rev. B, 2012. V. 86. P. 064416.

22.           Голикова Т.Е., Хюблер Ф., Бекманн Д., Кленов Н. В., Бакурский С. В., Куприянов М.Ю., Батов И. Е., Рязанов В.В. // Критический ток в планарных джозефсоновских S-N-S системах. Письма в ЖЭТФ, 2012.  т. 96, № 10, с. 743-748.

23.           Naoto Nagaosa, et. al. // Rev. Mod. Phys., 2010. V. 82. P. 1539–1592.

24.           Frolov S., Stoutimore M., Crane T. et al. Imaging spontaneous currents in superconducting arrays of pi-junctions // Nature Physics, 2008. V. 4. P. 32 - 36.

25.           A. Buzdin, A. E. Koshelev, Periodic alternating 0- and π-junction structures as realization of φ-Josephson junctions // Phys. Rev. B, 2003. V. 67. P. 220504.