УДК 621.396.697

Формирование трехмерных радиоизображений космических объектов по совокупности одномерных и двумерных проекций

 

С. В. Куликов, Д. Д. Садов, Д. С. Смолев

Открытое акционерное общество "Научно-производственный комплекс "Научно-исследовательский институт дальней радиосвязи"

Статья получена 28 апреля 2014 г.

 

Аннотация. Одномерные и двумерные радиоизображения объектов, построенные по информации широкополосных РЛС, рассматриваются в работе как совокупность проекций объекта, полученных для различных ракурсов на соответствующие направления  и плоскости. Применение к полученным проекциям томографического подхода обеспечивает возможность построения трёхмерных радиоизображений объектов. В работе представлены результаты моделирования алгоритмов построения трёхмерных радиоизображений вращающихся и стабилизированных космических объектов по их одномерным и двумерным радиоизображениям.

Ключевые слова: радиоизображение, 3D, томография.

Abstract: One-dimensional and two-dimensional radio images of objects, built by broadband RADARS information. They are considered as a projection object obtained for different camera angles to directions and planes. Application of tomographic projections to approach provides the ability to build 3D radio images. The article presents the results of modeling algorithms build 3D radio images for rotating and stable space objects by their one-dimensional and two-dimensional radio images.

Keywords: radio image, three-dimension, tomography.

 

Введение

Применение широкополосных сигналов в радиолокации обеспечивает возможность непосредственного формирования одномерных радиоизображений (дальностных портретов) объектов, а при использовании метода обратного синтеза апертур и двумерных изображений – проекций видимых «блестящих точек» на плоскость «линия визирования-вектор скорости объекта». Рассматривая построенные одномерные и двумерные радиоизображения как совокупность проекций объекта, полученных для различных ракурсов на соответствующие направления  и плоскости, и используя томографический подход можно формировать трёхмерные радиоизображения. Наиболее благоприятные условия для реализации указанной возможности возникают при достаточно хорошо известных и стабильных траектории объекта и закона движения относительно центра масс, что характерно для космических объектов (КО). В настоящей работе рассматриваются задачи формирования трёхмерных радиоизображений вращающихся объектов по совокупности дальностных портретов и  объектов с трёхосной стабилизацией по двумерным изображениям, полученным при зондировании КО на нескольких участках одной проводки, на различных витках КО, а также по информации от различных РЛС. 

Формирование трёхмерных радиоизображений вращающихся объектов по совокупности дальностных портретов

Лоцирование вращающихся объектов обеспечивает получение за один сеанс наблюдения существенно большего объёма информации. Этот объём зависит от ракурса наблюдения, он максимален, как и в задаче радиоастрономии [2], при углах jмежду линией визирования и осью вращения объекта 45 и 135 градусов. Указанная зависимость делает необходимым выбор соответствующего участка орбиты космического объекта. При длительности сеанса наблюдения не менее периода вращения объекта и указанных значениях угла между линией визирования и осью вращения объекта за один сеанс наблюдения подвергается зондированию большая часть поверхности объекта, причём значительная часть – в каждом зондировании, что создаёт  условия для построения трёхмерных изображений.

В работе используются две прямоугольные системы координат (СК).Центры обеих СК совпадают с центром масс объекта. Первая СК (x,y,z) связана с объектом и вращается вместе с ним с постоянной угловой скоростью. Осьzсовпадает с осью вращения объекта. Отражательные характеристики  объекта задаются функцией .

Ось ζ второй  СК (ξ,η,ζ) совпадает  с линией визирования. Ориентация осей x,yпервой СК и ξ,η второй СК могут задаваться произвольно, исходя из удобств пересчёта из одной СК в другую.

Радиолокатор, по информации которого формируются трёхмерные радиоизображения, обладает высоким разрешением по дальности (элемент разрешения значительно  меньше размеров объекта), а ширина диаграммы направленности радиолокатора много больше угловых размеров объекта.

Дальностные портреты, представляющие собой одномерные массивы амплитуд сигналов в каналах дальности, формируются в каждом периоде зондирования  на этапе первичной обработки радиолокационной информации.

Формируемые в каждом периоде зондирования массивы амплитуд сигналов в каналах дальности являются проекциями элементов объекта на линию визирования , j – номер канала дальности:

,

где  - распределение амплитуд по каналам дальности (по номерам j) при наличии одного точечного отражателя (блестящей точки, локального центра рассеяния) с координатой  в СК,  - коэффициент пересчёта отражательных характеристик в амплитуды.

Построение радиоизображения выполняется в два этапа. На первом производится формирование суммарного изображения объекта методом обратного проецирования. На втором этапе производится восстановление изображения, при этом в качестве начального приближения используется суммарное изображение. 

Обратное проецирование  в рассматриваемом случае состоит в последовательном отображении плоских слоёв  (каналов дальности ) из СК (ξ,η,ζ) в СК (x,y,z) и суммировании по всем проекциям и во всех   точках   области построения  изображения (куба, шара). В результате формируется суммарное изображение

,                                                                    (1)

где  – отображение проекции из СК (ξ,η,ζ) в СК (x,y,z)(обратная проекция), i – номер проекции (зондирования), N – число проекций.  

Суммарное изображениесвязано с исходной функцией  интегральным соотношением

=,           (2)

где –импульсная переходная функция линеаризованной модели  системы построения радиоизображения (реакция на один точечный отражатель),   – шум. Для решения уравнения (2)  относительноисходной функции  целесообразно  использовать итерационный метод с нелинейными ограничениями, не требующий нахождения оператора обратного преобразования [2]:

 ,

где x=(x,y,z), λ – параметр, управляющий сходимостью процесса,  – суммарное изображение,  I – единичный оператор, A – оператор преобразования исходного изображения в принятое (суммарное), E – оператор нелинейного преобразования, n – номер итерации.

Оператор A преобразования исходного изображения в суммарное реализуется соотношениями (1), (2). Оператор E нелинейного преобразования использует прежде всего общее свойство изображений, формируемых с использованием некогерентного накопления – положительность интенсивностей изображения во всех элементах разрешения. Другие нелинейные процедуры используют априорную информацию об объекте – о его размерах, об отражательных характеристиках объекта. В частности, если в отражённом от объекта сигнале преобладают сигналы, рассеянные локальными центрами (блестящими точками), информация об этом позволяет существенно повысить качество изображения. Используемая для этого процедура в каждой итерации выделяет локальные максимумы в трёхмерном массиве  и обнуляет интенсивности в остальных элементах разрешения, а также и «слабые» локальные максимумы. Применение этой процедуры обеспечивает в модели достаточно быстрое приближение формируемого изображения к исходному. Однако дальнейшее её применение может приводить к исключению из изображения точек, соответствующих истинным блестящим точкам объекта. При наличии априорной информации о количестве блестящих точек она может быть использована для остановки итерационной процедуры либо для исключения из итогового изображения «лишних» точек.

В отсутствие априорной информации о количестве блестящих точек может быть применена процедура, направленная на выделение наиболее «ярких» точек. При этом в качестве порога может быть использовано значение амплитуды, при котором в упорядоченном по убыванию массиве реализуется максимальная крутизна.

Таким образом, решение задачи формируется последовательным (многократным) применением прямого преобразования, связывающего суммарное изображение объекта с исходным, с применением мер по обеспечению устойчивости решения в условиях воздействия  шумов, а также (на каждой итерации) нелинейных преобразований, основанных главным образом на использовании априорной информации о восстанавливаемом изображении [2].

На качество формируемого изображения могут оказывать влияние ошибки в используемой при обработке информации о параметрах движения объекта, как его центра масс, так и относительно центра масс. Представляют интерес прежде всего ошибки радиальной скорости центра масс , ориентации оси вращения объектаdu, периода вращения объекта.

Ошибка в оценке ориентации оси вращения объектаdu не будет существенной, если D/2*du<d,гдеD – размер КО, d – разрешающая способность РЛС.

Ошибка в оценке периода вращения объекта не приведёт к существенному искажению изображения, если p**T/ *D<d.

При D=10м, d=0.2м, T==15сзначения ошибок не должны превышать du»2.2град,d» 0.1c, что в настоящее время представляется реализуемым.

Процедуры построения изображений наиболее критичны к ошибкам радиальной скорости центра масс . Для выполнения условия *T<dнеобходимо <0.014м/с. Ошибки оценок радиальной скорости  могут быть существенно больше полученного выше критического значения (1.4см/с), что приведёт к искажению изображения. В этих условиях повышение качества изображения может быть достигнуто повторением процедуры формирования изображения при различных гипотезах об истинном значении радиальной скорости  и выборе изображения, для которого принятый показатель качества (контрастность, резкость) окажется максимальным.

Наилучшие условия для построения изображения объекта возникают, когда на одном витке на различных его участках реализуются оба значения угла j между линией визирования и осью вращения  (45 и 135град). Такие условия реализуются в частности, если «на параметре» ориентация оси вращения совпадает  с орбитальной скоростью объекта (или мало отличается от неё). При этом в процессе зондирования на двух участках проводки информация об объекте получается в полном телесном угле и минимизируются потери, вызванные затенением элементов объекта. В этих условиях перед обработкой возникает дополнительная задача – объединение двух «половинок» изображения, полученных на двух ракурсах. Становятся более жёсткими требования к ошибкам оценок параметров движения объекта, прежде всего оценок периода вращения.  Однако для адаптации к ошибкам дальности (в рассматриваемом случае эту ошибку уже нельзя считать постоянной) и периода вращения нет необходимости пересчитывать дальностные портреты и изображения. Достаточно уже сформированные «половинки» изображения «двигать» по оси вращения - для компенсации ошибок дальности и вращать вокруг оси вращения объекта - для компенсации сдвига фазы вращения, «набежавшего» из-за ошибки  за время движения КО между участками проводки (сотни секунд). Эти операции можно  реализовывать в интерактивном режиме.

На рис.1-4 показаны результаты моделирования алгоритма формирования трёхмерных изображений вращающихся объектов. Моделирование проводилось для следующих условий:

·        объект в форме радионепрозрачной сферы с радиусом R=5м и с расположенными на её поверхности 18 блестящими точками (8 на экваторе, по 1 на полюсах, по 4 на двух промежуточных поясах);

·        разрешающая способность РЛС 0.2м;

·        орбита близка к круговой с высотой 500км;

Зависимость угла jмежду осью вращения объекта и  линией визирования от времени представлена на рис.1, из которого видно, что на траектории реализуются оба указанные выше значения угла j (45 и 135град).

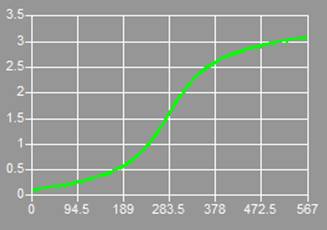
Рис.1.Зависимость угла (в радианах) между осью вращения объекта и линией визирования от времени (в секундах)

На рис.2 показано изображение, построенное при прохождении объектом угла j=45град. На графике присутствуют все 8 точек экваториального пояса (в нижней части изображения), точка на полюсе и 4 точки промежуточного пояса. На рис.3 – то же для  угла j=135град. На рис.4 показана сумма изображений рис.2,3, сформированных для углов между осью вращения объекта и линией визирования j=45град  и j=135град. Различные цвета выделенных элементов (блестящих точек) соответствуют различным оценкам их яркостей.

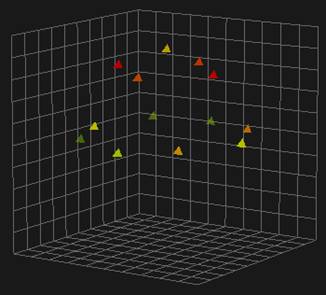
Рис.2. Изображение, построенное при прохождении объектом угла между осью вращения объекта и линией визирования j=45град.

Рис.3.Изображение, построенное при прохождении объектом угла между осью вращения объекта и линией визирования j=135град.

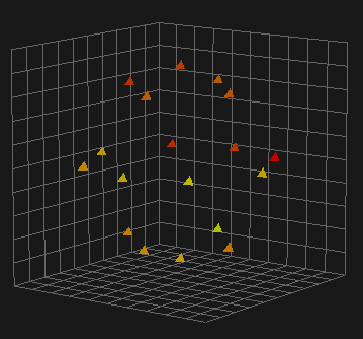
Рис.4. Сумма изображений, сформированных для углов между осью вращения объекта и линией визирования j=45град  и j=135град.

Формирование трёхмерных радиоизображений  объектов с трёхосной стабилизацией по двумерным изображениям

Для формирования трёхмерных радиоизображений  объектов с трёхосной стабилизацией по двумерным изображениям может использоваться информация, получаемая при зондировании КО на нескольких участках одной проводки, на различных витках КО, а также информация от различных РЛС.  Суммарное количество исходных двумерных изображений может составлять несколько десятков.  Оно существенно меньше числа одномерных проекций, получаемых при зондировании вращающихся объектов, что повышает роль процедуры восстановления. Однако информативность двумерных изображений значительно выше, что наглядно проявляется при обратном проецировании:  если обратной проекцией точки в одномерной проекции является плоскость, то обратной проекцией точки в двумерном изображении – прямая.  При совместной  обработке информации, полученной при различных ракурсах и дальностях, в различное время, на различных средствах необходимо решать задачу совмещения «центров» частных изображений, что может потребовать значительных вычислительных затрат. Однако при  времени сбора исходной информации несколько часов или десятков часов требования к времени обработки не должны быть слишком жёсткими.

Рассматривалось движение КО с двумя видами трёхосной стабилизации. Первый - в инерциальной системе координат (СК). Второй -  в подвижной орбитальной СК, связанной с объектом, одна из осей которой направлена к центру Земли, две другие связаны с плоскостью орбиты. Оценка информативности и качества формируемых трёхмерных радиоизображениий проводилась моделированием для круговой орбиты с высотой 500км и наклонением 45град. Как и ранее, имитировался объект в форме  радионепрозрачной сферы с радиусом R=5м и с расположенными на её поверхности 18 блестящими точками. Двумерные портреты, получаемые методом обратного синтеза апертур, имитировались проецированием видимых (с учётом затенения) блестящих точек на плоскость, содержащую вектор скорости КО и линию визирования.

Для КО, стабилизированного в инерциальной СК, при зондировании с одной РЛС, расположенной на экваторе, результаты моделирования аналогичны полученным для вращающихся КО (рис.2,3,4).Первое частное изображение формировалось по информации, полученной на трёх смежных витках, на каждом из которых формировались двумерные изображения через 20с с ограничениями: угол места не менее 5град, дальность не более 1500км. Второе частное изображение формировалось аналогичным образом через 12 часов после первого, когда КО наблюдался с РЛС с противоположной стороны. Общее число двумерных изображений составило ~30. Оба эти изображения ввиду радионепрозрачности сферы воспроизводили объект не полностью. Третье изображение, полученное по всей информации (суммированием двух частных изображений), воспроизводит объект в полном телесном угле.

При смещении точки наблюдения (стояния РЛС) в направлении средних широт (при выполнении условий наблюдаемости КО с учётом наклонения орбит[3]) яркости точек, чаще попадающих в зону затенения, падают. При наличии двух среднеширотных РЛС, расположенных в южном и северном полушариях, на объединённом изображении  выделяются все 18 блестящих точек.

Условия наблюдения КО со вторым типом стабилизации (в подвижной орбитальной СК, связанной с объектом)  характеризуются тем, что информация, получаемая через 12 часов, мало отличается от полученной ранее, в результате чего трёхмерное изображение может быть построено не в полном телесном угле. Информация от других РЛС также существенно не увеличивает возможности построения трёхмерных изображений. 

Результаты исследования

Использование томографического подхода обеспечивает построение трехмерных радиоизображений вращающихся космических объектов. При этом необходимо достаточно точно знать движение объекта, как его центра масс, так и относительно центра масс. По результатам моделирования видно, что восстановление трехмерного радиоизображения этим методом – принципиально возможно (рис.5, 6).

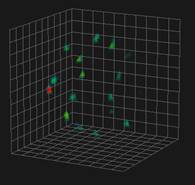
Рис.5. Изображения КО, стабилизированного в инерциальной СК. Левое построено по информации, полученной на трёх смежных витках, в центре - построено также по трём смежным виткам через 12 часов, правое изображение построено по всей информации.

 

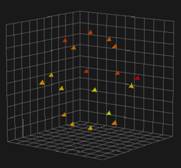
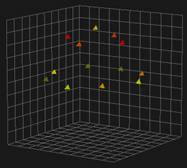
Рис.6. Изображения вращающегося объекта, построенные при прохождении объектом углов j=45град (левый график) и j=135град (правый график) и их сумма (средний график).

Выводы

Использование томографического подхода обеспечивает построение трехмерных радиоизображений по совокупности проекций (одномерных и двумерных изображений) объекта, полученных для различных ракурсов на соответствующие направления  и плоскости.

Для вращающихся объектов трехмерные радиоизображения могут быть построены по совокупности одномерных проекций (дальностных портретов) объектав полном телесном угле, если в одной проводке на различных её участках объект наблюдается при значениях углов между осью вращения и линией визирования ~45 и ~135град.

Для объектов, стабилизированных в инерциальной СК, трехмерные радиоизображения могут быть построены по совокупности двумерных изображений в полном телесном угле по информации от одной РЛС, расположенной в районе экватора, либо от двух среднеширотных РЛС, для которых выполняются условия наблюдаемости КО с учётом наклонения орбит.

Для объектов, стабилизированных в подвижной орбитальной СК, связанной с объектом, трехмерные радиоизображения могут быть построены по совокупности двумерных изображений не в полном телесном угле. 

 

Литература

1. Агафонов М.И., Шарова О.И. Томография при ограниченном числе проекций. II.Радиоастрономический подход cleanв приложении к трёхмерным задачам. ИВУЗ, Радиофизика, том 48,№5,2005г.,Нижний Новгород.

2. Василенко Г.И., Тараторин А.М. Восстановление изображений. М, Радио и связь,1986.

3. Детков А.Н., Макаров И.А. Модель движения космического объекта и формирование его радиолокационного портрета // Журнал радиоэлектроники: электронный журнал. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/11/text.pdf