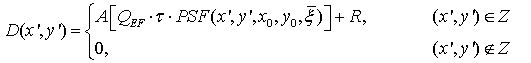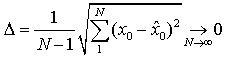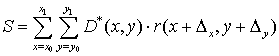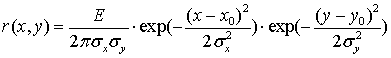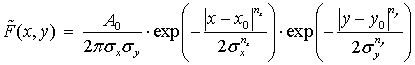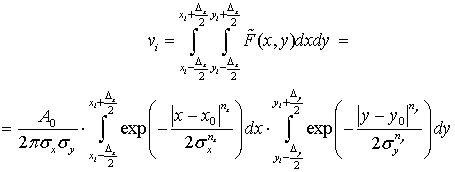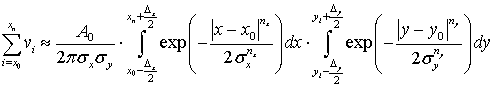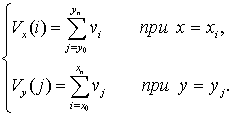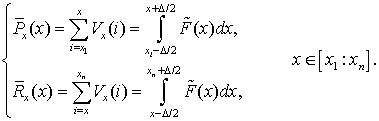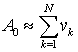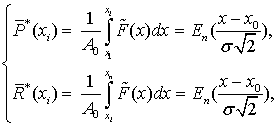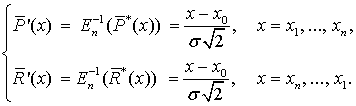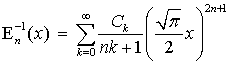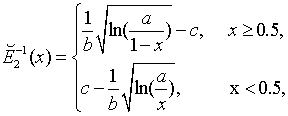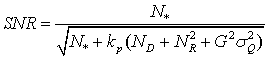МЕТОД СУБПИКСЕЛЬНОГО ИЗМЕРЕНИЯ КООРДИНАТ ИЗОБРАЖЕНИЙ ЗВЕЗД ДЛЯ ПРИБОРОВ АСТРООРИЕНТАЦИИ КОСМИЧЕСКОГО БАЗИРОВАНИЯ
И. С. Осадчий
Научно-производственное объединение «Лептон»
Статья получена 27 апреля 2015 г.
Аннотация. Рассматривается задача измерения координат фотоцентров изображений звезд с субпиксельной точностью для приборов астроориентации космического базирования. Рассмотрен метод измерения с помощью взаимно корреляционной функции и наиболее часто применяемый метод взвешенных сумм. Описан предлагаемый метод аналитического расчета координат, не требующий большого объема вычислений и межпиксельного шага сканирования изображения. Произведен сравнительный анализ предложенного и ранее рассмотренных методов по сложности вычислений и величинам систематической и случайной ошибки измерения.
Ключевые слова: приборы астроориентации, измерение координат звезд, взвешенные суммы.
Abstract. In this article described the problem of measurement of star image with subpixel accuracy for space-based Star tracker. The cross-correlation function method and most usable The Center of gravity method were considered. New method of analytical measurement has been suggested. This method do not require big calculations and step of image processing less than one pixel. Comparative analysis of described methods was performed.
Keywords: star trackers, centroid methods, center of gravity.
Введение
В современных космических аппаратах широкое применение находят оптико-электронные приборы астроориентации, использующие в качестве ориентиров звезды [1]. Одной из задач решаемой в таких приборах является измерение координат фотоцентров изображений звезд, регистрируемых с помощью матричного фотоприемного устройства (ФПУ). При этом от точности измерений зависит как вероятность правильной идентификации объектов [2], так и погрешность вычисления ориентации оси визирования [3].
Однако в связи со спецификой космического базирования приборы подобного класса не обладают большими вычислительными возможностями, поскольку в их составе требуется применение радиационностойких вычислительных устройств при минимизации как массогабаритных характеристик, так и параметров энергопотребления. В связи с этим, приоритетным направлением развития методов измерения координат фотоцентров изображений звезд является достижение как можно меньшей ошибки измерений при минимально возможном использовании вычислительных ресурсов.
Постановка задачи
Распределение интенсивности светового потока 
от звезды на поверхности ФПУ определяется
сверткой между функцией рассеяния точки оптической системы и апертурой пикселя [4]:
|
|
(1) |
где 
–
энергия от звезды, попадающая на плоскость регистрации, 
–
координаты осей ФПУ, 
– фотоцентр изображения звезды,
– функция рассеяния точки, 
– вектор параметров, определяющих её форму,
– функция аппретуры пикселя.
Функция является выпуклой,
ограниченной линейными размерами светочувствительного элемента и имеющей
максимум в его центре. В общем случае, вид функции является
неизвестным и изменяется под воздействием внешних факторов. Однако она является
неограниченной, симметричной относительно ярко выраженного максимума с
координатами и её значения резко убывают при удалении
от него.
На цифровом изображении функция представлена
сигнальным кластером отсчетов 
– дискретизированными
в пространстве и квантованными по уровням величинами оптического сигнала. Численные
значения определяется как квантовой эффективностью
ФПУ, так и временем экспозиции. При этом поскольку резко
убывает при удаления от центра, то для измерений можно выделить некоторую
область 
на плоскости регистрации, за пределами
которой считать воздействие оптического сигнала нулевым:
|
(2) |
где 
–
целочисленные координаты пикселей ФПУ, 
–
квантовая эффективность, 
– время экспозиции, 
– оператор квантования, 
– совокупный шум оптико-электронного
преобразования [5]. При этом астроприборы конструируется таким образом, чтобы характерный размер области составлял порядка 3×3
– 5×5 пикселей ФПУ [6].
В результате за счет применения метода измерения требуется получить
оценку 
координат максимума непрерывной функции интенсивности
светового потока по ограниченному набору цифровых отсчетов . Возникающая при этом ошибка 
состоит из трех основных компонент, две
из которых являются систематическими, а одна – случайной [7]:
|
|
|
где 
–
совокупная систематическая ошибка, 
– ошибка отклонения
реальной формы сигнала от цифрового представления, 
–
ошибка, возникающая за счет ограничения области распространения
оптического сигнала, 
– ошибка, обуславливаемая
стохастическими воздействиями на изображение звезды, такими как фотонный шум [8] и шумы оптико-электронного преобразования [5]. Однако, в общем случае, применяемый
метод измерения должен обеспечивать минимизацию общего среднеквадратичного
отклонения формируемых оценок положения от их истинного значения [9]:
|
|
(3) |
где 
– количество
произведенных измерений.
Так же немаловажным критерием для применения метода измерения в приборах астроориентации космического базирования является его работоспособность в режиме реального времени и в условиях ограничения вычислительных ресурсов [10]. При этом в качестве количественной оценки данного критерия целесообразно использовать необходимый методу объем математических операций.
Методы измерения
Одним из способов решения задачи измерения может является метод Взаимной корреляции, описанный в теории оптимального приема сигналов [11] и использованный для задач измерения координат в работах [12] и [13]. Для двух дискретных сигналов взаимная корреляционная функция определяется как
|
|
(4) |
где 
– комплексно
сопряженная функция принимаемого сигнала, 
–
ожидаемый сигнал, 
, 
–
сдвиг ожидаемого сигнала относительно принимаемого.
Для определения положения фотоцентра изображения звезды
производится вычисление корреляционной функции с шагами и
, меньших размера пикселей ФПУ примерно в
10 – 100 раз [14] и результатом измерений служат те значения сдвига, при
которых (4) принимает максимум.
В качестве функции , как
правило [15], выбирается приближенная форма в виде двумерной функции Гаусса:
|
(5) |
где E – суммарная энергия от точечного источника света, 
– координаты центра, 
, 
– параметры
ширины пятна.
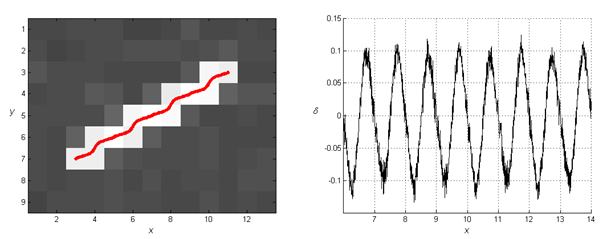
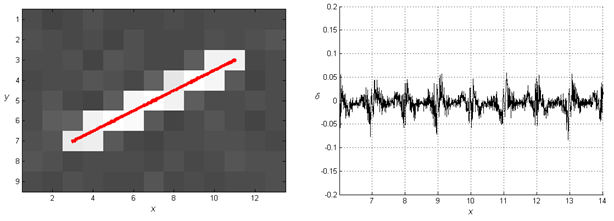
На Рисунке 1 представлен результат обработки тестового трека
от звезды данным методом с шагами сканирования 
:
слева на трек наложены зачитанные значения координат (красным), справа
изображен график отклонения одной из координат от её истинного значения.
|
|
|
Рисунок 1. Оценка координат звезды методом Взаимной корреляции |
Из представленного рисунка видно, что ошибка измерения для
данного метода в основном определяется величиной шагов сканирования и .
С помощью метода Взаимной корреляции возможно полное
исключение систематической ошибки измерения координат, при условии совпадения
функции с принимаемым сигналом и бесконечно малыми
шагами сдвига функций и относительно
друг друга. Однако поскольку ожидаемый сигнал зависит
от положения его центра по отношению к решетке дискретизации (1), то на каждом
шаге сдвига и 
требуется
не только расчет взаимной корреляции, но и перерасчет его значений. В результате
данный метод по меркам астроприборов требует достаточно больших вычислительных
ресурсов, что делает его применение в их составе весьма затруднительным.
В связи с вычислительной сложностью метода Взаимной корреляции, наиболее широкую популярность приобрел метод Взвешенных сумм (Center of Gravity) [16]. Он обладает несложной реализацией, простой процедурой вычисления и относительно высокой точностью получаемых значений.
В данном методе оценка координат
положения фотоцентра определяется как
|
|
|
где xi, yi – координаты отсчетов на изображении по горизонтальной и вертикальной оси соответственно, vi – значения отсчетов, N – общее количество элементов кластера. За счет такого вычисления учитываются все отсчеты изображения звезды, и получаемая оценка имеет субпиксельную точность.
На Рисунке 2 (слева) представлена модель трека от
линейно движущегося точечного источника света по плоскости ФПУ, на который
наложены измеренные координаты фотоцентра, а справа на данном рисунке
показано отклонение получаемой оценки координаты 
от её
истинного значения. Из представленного рисунка видно, что по каждой из осей отклонение
представляет собой периодическую функцию, огибающую истинную координату
фотоцентра по гармоническому закону [17].
|
|
|
Рисунок 2. Оценка координат звезды методом Взвешенных сумм |
Такое явление возникает за счет того, что в данном методе не
производится восстановление формы непрерывного распределения оптического
сигнала , а используются только цифровые значения
отсчетов. При этом амплитуда таких отклонений сильно зависит от соотношений
размера пятна к шагу пространственной дискретизации и при определенных условиях
может составлять до половины размера пикселя, что является значительным
недостатком данного метода.
Предлагаемый метод измерения
Предлагаемый метод измерения схож с описанным в работе [18] теоретическим подходом, направленным на аналитический расчет координат с помощью аппроксимации непрерывной функции распределения светового потока по набору дискретных данных, однако предлагаемый метод имеет намного меньшую ресурсоемкость вычислений и предназначен для применения в составе астроприборов космического базирования.
Для восстановления непрерывной формы распределения
интенсивности светового потока , попадающего от звезды
на плоскость ФПУ, в предлагаемом методе предлагается её аппроксимация обобщенной
функцией распределения ошибок [19]:
|
(6) |
где 
–
энергия излучения от звезды, – положение максимума,
– ширина пятна по горизонтальной и
вертикальной оси, а 
– параметры внутренней формы
пятна рассеяния.
Отличием 
от применяемой в
подавляющем большинстве методов измерения функции двумерного распределения
Гаусса (5) является введение дополнительных параметров 
и
. На Рисунке 3 представлен профиль (6) по
оси 
с несколькими различными значениями
параметра .
|
|
|
Рисунок 3. Предлагаемая функция
аппроксимации с различными значениями параметра |
Из рисунка видно, что при 
предлагаемая
функция аппроксимации представляет собой функцию Гаусса, при 
появляется более ярко выраженный пик и
форма пятна стремится к треугольной, а при 
форма
становится более пологой и стремится к цилиндрической. При правильном
теоретическом расчете или корректном подборе параметров функции аппроксимации (6)
экспериментальным путем можно значительно уменьшить её отклонение от реальной
формы пятна, что снизит систематическую ошибку измерений.
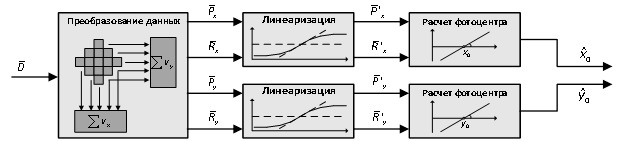
На Рисунке 4 изображена структурная схема основных действий, необходимых для определения координат фотоцентра звезды в двумерном пространстве по набору отсчетов изображения.
|
|
|
Рисунок 4. Структурная схема предлагаемого метода |
На представленной схеме в качестве исходных данных
рассматривается множество дискретных данных 
:
|
|
|
представляющих собой сигнальный
кластер отсчетов изображения. Каждый элемент данного множества состоит из трех
компонент: 
– координата отсчета по горизонтальной
оси, 
– координата отсчета по вертикальной оси,
– накопленное ФПУ значение в данном
отсчете. Общее количество элементов множества обозначено за .
Преобразование данных. Первым этапом обработки
является преобразование поступающих данных в последовательности интегральных
сумм 
и 
для
измерения фотоцентра по горизонтальной оси изображения
и последовательности интегральных сумм 
и 
для измерения фотоцентра по вертикальной
оси 
изображения.
Поскольку значение каждого
поступающего на вход отсчета сигнального множества представляет
собой накопленное за время экспозиции количество фотоэлектронов в пикселе ФПУ с
координатами и [20], то с учетом функции аппроксимации (6) оно может быть представлено как:
|
|
|
где –
линейные размеры пикселя по горизонтали, –
линейные размеры пикселя по вертикали. Исходя из этого, для набора соседних на
изображении отсчетов, расположенных вдоль одной из осей, можно записать
|
(7) |
и для измерения координат фотоцентра
возможно преобразование входного множества данных в виде
двух одномерных последовательностей сумм отсчетов:
|
|
(9) |
В результате измерение положения фотоцентра по
горизонтальной оси возможно производить с помощью
ряда 
, а измерение по вертикальной оси 
с помощью 
.
Каждый отсчет в и представляет собой интегральное значение
интенсивности светового потока от звезды, попавшего на прямоугольную область
ФПУ шириной в один пиксель, и последовательные суммы их значений будут
представлять собой результаты интегралов по постепенно расширяющейся в
ортогональном направлении области:
|
|
(10) |
При этом представляет собой
правостороннюю последовательность интегральных сумм при инкрементировании от минимального значения 
до максимального 
,
а является левосторонней
последовательностью, то есть полученной при декрементировании от до . Выражение (10) так же может быть
применено к для получения последовательности сумм и
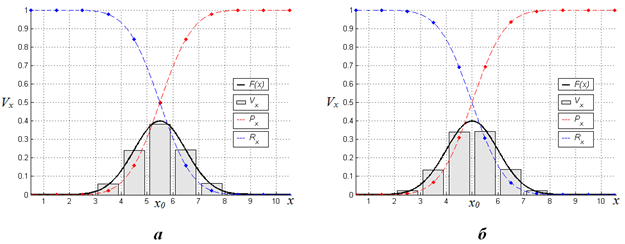
На Рисунке 5 представлены примеры преобразования данных в
предлагаемом методе измерения для горизонтальной оси изображения. На (а)
положение фотоцентра звезды совпадает с серединой пикселя ФПУ, а на (б)
положение фотоцентра приходится на стык соседних пикселей. По горизонтальной
оси на обоих рисунках отображены номера столбцов
изображения, а по вертикальной оси обозначены значения полученных сумм (9), которые изображены в виде
прямоугольников серого цвета. Черной сплошной линией выделена непрерывная
функция распределения интенсивности светового потока, построенная в
соответствии с предлагаемой функцией аппроксимации , координата
её максимума обозначена за 
. Значения полученных в
соответствии с (10) последовательностей интегральных сумм и обозначены
в виде точек красного и синего цвета соответственно. Для наглядности так же
изображены непрерывные значения интегралов (7) в виде пунктирных линий.
Из представленного рисунка видно, что значения рядов и представляют
собой значения интегралов от формы пятна в точках, соответствующих центрам
пикселей ФПУ вне зависимости от положения фотоцентра звезды .
|
|
|
Рисунок 5. Сформированные последовательности сумм по исходным данным |
Линеаризация и измерение. Поскольку в предлагаемом
методе дальнейшие этапы измерения осуществляются одинаково и независимо по
обеим осям (рисунок 4), то последующие действия будут описываться для
горизонтальной оси .
Перед непосредственным измерением производится линеаризация ранее
полученных интегральных рядов и . Если осуществить сдвиг и нормировку их
значений как
|
|
|
где 
–
суммарное количество энергии, накопленное ФПУ от попадания на его поверхность
света от звезды, которое может быть найдено как сумма всех сигнальных отсчетов
поступающего на обработку кластера:
|
|
|
то выражение (10) можно выразить через обобщенную функцию ошибок [21]:
|
|
|
где –
истинное положение фотоцентра звезды на рассматриваемой оси изображения, 
– параметр ширины, а индекс 
у обобщенной функции ошибок представляет
собой параметр аппроксимации формы пятна в (6).
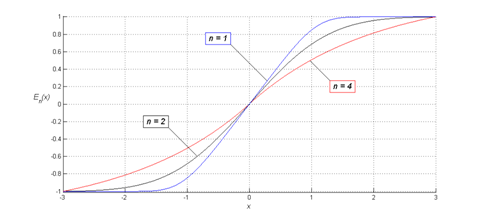
Частным случаем обобщенной функции ошибок 
при параметре является функция 
. На Рисунке 6 представлен вид графиков при различных значениях параметра и положении фотоцентра 
.
|
|
|
Рисунок 6. Обобщенная функция ошибок при различных значениях параметра n |
Из представленного рисунка видно, что данная функция
является монотонно возрастающей на всей области определения и принимает нулевое
значение в точке, соответствующей максимуму аппроксимации 
. При этом параметр влияет на крутизну возрастания: при его
уменьшении появляется более выраженный перегиб при подходе к экстремальным
значениям, а при его увеличении вид данной функции приближается к линейному.
Поскольку на всей области
определения является монотонно возрастающей, то для неё существует обратная
функция [22], такая что
|
|
|
и при её применении к сформированным
нормированным последовательностям интегральных сумм 
и 
данные значения будут описываться
уравнением прямой:
|
(11) |
На Рисунке 7 представлены полученные линеаризованные данные 
и 
для
профилей изображений звезды, показанных на Рисунке 5.
|
|
|
Рисунок 7. Линеаризация последовательностей сумм по набору дискретных данных |
Численные значения 
и
прямая, на которой они располагаются, изображены красным цветом, а значения и их прямая показаны синим цветом. Из
данных рисунков видно, что положению фотоцентра 
соответствует
точка пересечения прямых с осью .
В результате оценка координаты по каждой из прямых выражается как
|
|
|
и, поскольку при реальном измерении положения фотоцентра имеют место шумовые воздействия, то конечным результатом является среднее значение:
|
|
|
Вычисление обратной функции. Наибольшую
вычислительную сложность в предлагаемом методе оценки координат фотоцентра
звезды составляет вычисление обратной функции к обобщенной функции ошибок в
выражении (11). Она относится к классу специальных и не может быть рассчитана
аналитическим путем в общем виде [23], однако, из частного случая при 
в [24] можно получить её разложение в
ряд:
|
(15) |
где 
–
рекурсивно вычисляемые коэффициенты. 
,
|
|
|
Данное выражение является относительно простым для
практических вычислений, однако оно имеет крайне низкую сходимость при
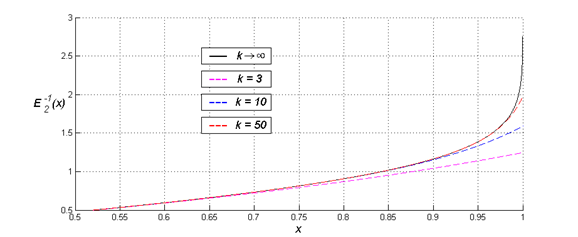
приближении функции к асимптотическим границам. На Рисунке 8 изображена
обратная функция ошибок 
с параметром 
и семейство графиков, рассчитанных с
помощью (15) при различном количестве 
используемых
слагаемых. На графике черным цветом показана функция при
.
|
|
|
Рисунок 8. Вычисление с помощью разложения в ряд обратной функции к обобщенной функции ошибок |
Из представленного семейства графиков видно, что ряд (15)
достаточно быстро сходится на линейном участке и крайне медленно сходится на
изгибах даже при очень большом количестве слагаемых. Для достижения приемлемой
точности вычислений требуется порядка 
слагаемых,
что на сегодняшний день является невозможным для расчета в специализированных
цифровых вычислителях, используемых в составе астроприборов.
В работе [25] дана другая аппроксимация для обратной функции
ошибок с параметром , которая выражается как
|
|
|
где 
– функция
аппроксимации, 
, 
, 
.
Данная аппроксимация была расширена на произвольные значения параметра n, и итоговое выражение для расчета обратной функции к обобщенной ошибок принимает вид
|
|
|
По результатам оценок, отклонение предлагаемой аппроксимации
от обратной функции к обобщенной функции ошибок составило порядка 0.08, что
соответствует вычислению с помощью разложения в ряд (15) при использовании
порядка 
слагаемых.
В результате предлагаемая функция аппроксимации 
является достаточно простой для
практических расчетов и при этом имеет небольшие отклонения от обратной функции
к обобщенной функции ошибок 
.
Пример обработки. В качестве примера работы предлагаемого метода измерения на Рисунке 9 (слева) представлена модель трека, на который наложены полученные положения фотоцентра в виде точек красного цвета. Справа на рисунке изображен график их отклонений от истинного значения.
|
|
|
Рисунок 9. Оценка координат звезды предлагаемым методом |
Из представленного рисунка видно, что получаемые координаты
с большой точностью соответствуют траектории движения звезды, а размах
отклонений имеет порядок 
.
На Рисунке 10 представлены графики отклонений 
от истинных значений, полученных по
результатам обработки этого же трека с оптимально подобранными параметрами
функции аппроксимации и , но
различными значениями параметров и .
|
|
|
Рисунок 10. Оценка координат звезды при различных значениях параметра n |
Из представленных графиков видно, что изменение параметров и значительно
влияет на снижение систематической ошибки измерения координат положения
фотоцентра звезды.
Сравнительный анализ
Вычислительная сложность. Оценку вычислительной сложности для предлагаемого метода измерения (ПМИ) можно дать исходя из количества вычислительных операций, требующихся для получения оценки координат.
В Таблице 1 представлены
зависимости количества различных типов вычислительных операций, использующихся
в ПМИ, от общего количества отсчетов и протяженностей 
и 
сигнального
кластера по горизонтальной и вертикальной оси изображения соответственно. Так
же в данной таблице указаны аналогичные зависимости для метода Взаимной
корреляции (ВК) с шагом сканирования 
, метода Взвешенных
сумм (CoG) и теоретического подхода к измерению на
основе интерполяции функции ошибок (ИФО) [18].
|
Таблица 1. Зависимость количества операций от размеров кластера |
|
||||
|
Операция |
ПМИ |
ВК |
CoG |
ИФО |
|
|
Сумма |
|
|
|
|
|
|
Произведение |
|
|
|
|
|
|
Деление |
|
|
|
|
|
|
Возведение в степень |
|
|
0 |
|
|
|
Логарифмирование |
|
0 |
0 |
0 |
|
На Рисунке 11 отображена в логарифмическом масштабе
зависимость вычислительной сложности от размера сигнального кластера для данных методов в предположении, что
протяженности и равны
друг другу, сложность арифметических операций составляет 1 такт, а операций
возведения в степень и логарифмирования 50 тактов.
|
|
|
Рисунок 11. Зависимость количества операций от размера кластера для различных методов |
Из представленных графиков видно, что при описанных
приближениях сложность ПМИ уступает только вычислительной сложности метода CoG, но при этом она значительно ниже, чем вычислительная
сложность метода ИФО и метода ВК. В среднем ПМИ требует в 7 раз больше
вычислений по отношению к методу CoG и при этом
в 13 раз меньше по отношению к методу ИФО, и в 40 раз меньше по отношению к
методу ВК при шаге сканирования 
пикселя.
Систематическая
ошибка. Для исследования и сравнительного анализа величины систематической
ошибки измерения координат проводился эксперимент численного моделирования. В
ходе данного эксперимента генерировался профиль пятна в виде функции Гаусса (5)
и для каждого значения ширины осуществлялось
перемещение вдоль оси положения истинного центра ,
которое в дальнейшем рассчитывалось с помощью методов CoG
и ПМИ. Отклонение получаемых оценок фотоцентра от его истинного значения для
каждого метода оценивалось с помощью выражения (3). На Рисунке 12 представлена
зависимость среднеквадратичного отклонения рассчитанной систематической ошибки для
исследуемых методов.
|
|
|
Рисунок 12. Зависимость ошибки измерения фотоцентра от ширины пятна для различных методов |
Из представленных графиков видно, что ПМИ обеспечивает
среднеквадратичное отклонение ошибки измерения координат от истинного значения
порядка 
пикселя ФПУ даже при малых значениях
ширины пятна, что является лучшим результатом. Принципиальное присутствие
систематической ошибки связано с ограничением набора цифровых отсчетов (2).
Случайная ошибка измерения. Для оценки величины влияния шумовой составляющей на получаемые с помощью ПМИ координаты положения фотоцентра так же проводился эксперимент численного моделирования.
В данном эксперименте для фиксированного положении и ширине профиля
пятна (5) к цифровым отсчетам добавлялись шум Пуассона, имитирующий фотонный
шум, и нормальный шум, имитирующий воздействие случайных процессов оптико-электронного
преобразования в ФПУ. Для каждого фиксированного соотношения сигнал/шум
производилось 1000 измерений положения фотоцентра с помощью различных методов.
На Рисунке 13 представлены результаты среднеквадратичного отклонения оценок координат фотоцентра от соотношения сигнал/шум, полученные для методов CoG и ПМИ.
|
|
|
Рисунок 13. Зависимость ошибки измерения от соотношения сигнал/шум для различных методов |
Для построения данной зависимости соотношение сигнал/шум вычислялось как [5]:
|
|
|
где 
–
количество пикселей, на которые распространяется световой сигнал от звезды, 
– количество накапливаемых
фотоэлектронов, 
– количество термоэлектронов в
одном пикселе, 
– шум считывания данных из
матричного приемника, выраженный в электрон/пиксель, 
–
шум усиления и квантования накопленного заряда за время экспозиции, выраженный
в количестве электронов на один квант АЦП.
Из представленных графиков видно, что отклонение оценок координат для ПМИ, вызванных наличием шумовой составляющей практически не отличается от тех же отклонений для метода CoG.
Заключение
В данной статье рассматривается задача измерения координат фотоцентра изображения звезды в плоскости ФПУ, являющаяся одной из основных для оптико-электронных приборов астроориентации космического базирования.
Сложность данной задачи заключается в необходимости определения по набору цифровых отсчетов изображения максимума непрерывной функции распределения интенсивности светового потока попадающего на плоскость регистрации от звезды. При этом форма распределения зависит как от оптико-электронного блока прибора, так и от расположения фотоцентра на площадке пикселя. В результате ошибка измерения может иметь как нелинейную систематическую составляющую, так и шумовую компоненту, вызванную природой сигнала и процессом оптико-электронного преобразования.
Рассмотрен оптимальный для решения данной задачи метод Взаимной корреляции, с помощью которого при определённых условиях возможно полностью устранить систематическую составляющую ошибки. Однако применение данного метода затруднительно в составе слабых вычислительных устройств астроприборов в связи с большим объемом требующихся операций.
Рассмотрен наиболее популярный метод Взвешенных сумм, обладающий простотой вычислений, но при этом имеющий большую систематическую ошибку отклонений координат при малых соотношениях размеров пятна к размерам пикселей ФПУ.
Предложен аналитический метод измерения, призванный минимизировать систематическую ошибку при сравнительно небольшом увеличении объема вычислений по отношению к методу Взвешенных сумм. Для предложенного метода введена функция аппроксимации непрерывного сигнала, за счет параметров которой возможно снизить неувязку между реальной формой пятна и её предполагаемым видом, используемым для вычислений.
Предложенный метод измерения базируется на применении обратной функции к обобщенной функции ошибок и не требует межпиксельного шага сканирования изображения. Для расчета обратной функции была расширена известная аппроксимация, имеющая простое вычисление и при этом обладающая хорошей точностью.
По результатам оценки вычислительных затрат сложность предлагаемого метода превосходит сложность метода Взвешенных сумм приблизительно в 7 раз, однако она меньше вычислительной сложность метода Взаимной корреляции при шаге сканирования изображения в 0.1 пикселя ФПУ в 40 раз.
По результатам численного моделирования систематическая
ошибка измерения в предлагаемом методе составляет порядка 
пикселя, что примерно в 1000 раз меньше,
чем ошибка метода Взвешенных сумм. При этом шумовая составляющая ошибки
измерения координат предлагаемым методом практически не отличается от шумовой
составляющей данного метода.