|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 1999 | |
Семенов В.С. Неведомский А.В. Дыбовский В.Г.
Сибирский физико-технический институт (СФТИ) при
Томском государственном университете
Поступила в редакцию 4 мая 1999
Предложена методика и приведено приближенное решение задачи дифракции плоской электромагнитной волны на двух идеально проводящих бесконечно-длинных круговых цилиндрах, расположенных в плоскослоистой среде. Разработанная методика представляет собой сочетание методов криволинейных координат, функции линейного источника и возмущений. Конечные выражения для компонент поля представлены в виде двойных рядов по модифицированным функциям Бесселя.В работе
[1] приведено решение задачи о расчете рассеянного электромагнитного поля от проводящего бесконечно длинного круглого цилиндра, расположенного в одном из слоев плоскослоистой земли. Рассматриваемая задача представляет значительный интерес в связи с разработкой эффективных методов зондирования неоднородных сред, в частности с обнаружением протяженных подземных коммуникаций типа трубопроводов в земле.В настоящей статье рассматривается случай двух проводящих цилиндров, что соответствует на практике групповой коммуникации. Исследование данных вопросов требует решения задачи дифракции электромагнитных волн на телах вращения.
Задачи теории дифракции, связанные с проблемой взаимодействия двух бесконечно длинных тел вращения изучен в меньшей степени, чем задачи дифракции на одиночных телах. Наиболее полный обзор работ сделан
[2]. Из последующих исследований в этом направлении можно отметить работы [1-8]. В этих публикациях строгими , либо приближенными методами рассматривается взаимодействие бесконечно протяженных цилиндрических тел (или тел какой либо другой формы) в безграничной среде, за исключением работы [6], где взаимодействующие тела находятся внутри непересекающихся цилиндрических поверхностях.1. Постановка задачи и метод решения.
Пусть в нижнем слое трехслойной плоскослоистой среды (
j=0,1,2) содержаться два параллельных бесконечно длинных проводящих круговых цилиндра с радиусом а-1 и а+1. Начало декартовой системы координат совпадает с границей раздела воздух - проводящая земля (z>0-воздух). Плоскость z=-d разделяет слои проводящей среды. Образующие цилиндров параллельны оси х. Плоская волна распространяется вдоль оси z, электрическая компонента которой направлена вдоль оси цилиндра (ось х). Требуется найти вторичное электромагнитное поле взаимодействующих цилиндров (рис. 1).Решение поставленной задачи может быть получено с помощью методики для одного цилиндра, рассмотренной в работе [1]. Взаимодействие между цилиндрами может быть учтено методом возмущений [2, 8]. Общая схема решения при этом выглядит следующим образом. Зная распределение тока на каждом цилиндре за счет воздействия первичного поля без учета взаимодействия цилиндров можно найти вектор-потенциал вторичного поля, рассеянного q-м цилиндром. Обозначим через
(v - порядок
рассеяния, q = ± 1)
потенциал вторичного поля в нижнем слое среды,
рассеянного q-м телом при воздействии на него
первичного поля без учета вторичного поля (v=1),
обусловленного наличием в слое второго цилиндра.
Потенциал, определяющий сумму вторичных полей,
отраженных от каждого цилиндра в отдельности
(при отсутствии другого), назовем потенциалом
вторичного поля в первом приближении
|
(1) |
Соответствующее распределение тока на цилиндрах будем называть распределением тока в первом приближении (или распределением 1-го порядка рассеяния, v=1).
Под действием поля первого порядка рассеяния q-го цилиндра (q=± 1) на другом цилиндре наведется поле второго порядка рассеяния (v=2), которому будет отвечать распределение тока второго порядка
и, соответствующий
этому распределению, потенциал 
. Для того, чтобы найти распределение
тока, необходимо, чтобы функция
|
(2) |
была решением волнового уравнения и удовлетворяла граничному условию на цилиндрической поверхности
:
|
или |
|
(3) |
||
Потенциал |
|
(4) |
|||
определяющий сумму вторичных полей первого и второго порядков рассеяния в слое j
(j=0, 1, 2), назовем потенциалом вторичного поля системы цилиндров во втором приближении и т.д. Процесс построения приближений для рассеянных полей распространяется на произвольное (бесконечное) число подобных шагов. Потенциал вторичного поля в S-ом приближении будет задаваться формулой
|
(5) |
Сумма
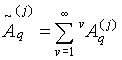является
потенциалом вторичного поля в слое j, рассеянного
одним из цилиндров в результате многократного
воздействия на него вторичных волн всех
последовательных порядков рассеяния,
возбужденных другим цилиндром в результате его
взаимодействия с первым цилиндром. Вторичное
поле системы цилиндров в каждом слое
определяется потенциалом
|
(6) |
2. Распределение тока на поверхностях взаимодействующих цилиндров
В соответствии с изложенным найдем распределение тока 2-го порядка рассеяния на q-ой цилиндрической поверхности (q± 1). Потенциал вторичного поля 1-го порядка рассеяния для q-го цилиндра в нижнем слое среды будем трактовать, как суммарный потенциал линейных токов индукции, наведенных на q-ом цилиндре первичным полем плоской волны и распределенных по поверхности Lq в соответствии с граничным условием на идеально проводящей цилиндрической поверхности [1]:
|
(7) |
где   |
(8) |
z1,2 - расстояние от верхней границы раздела до центра соответствующего цилиндра (рис. 1);
kj - волновое число j-слоя среды;
J1(j q) - функция распределения линейных токов индукции на цилиндрической поверхности Lq за счет воздействия первичного поля.
Удовлетворяя граничному условию (3) на поверхности цилиндра Lq, получим интегральное уравнение относительно плотности тока второго порядка рассеяния на q-ом цилиндре:
|
(9) |
здесь
при 
Левая часть уравнения (9) представляет собой совокупное значение потенциалов линейных токов индукции, наведенных на идеально проводящей р-ой цилиндрической поверхности плоской волной, в какой-либо точке наблюдения Mq на q-ой идеально проводящей цилиндрической поверхности.
Правая часть уравнения (9) представляет собой совокупное значение потенциалов линейных токов индукции, наведенных на q-ой идеально проводящей цилиндрической поверхности за счет воздействия поля р-го цилиндра, в той же текущей точке наблюдения Mq на q-ом цилиндре.
Условимся, что индекс q будет относиться к возбуждаемому цилиндру, то есть к цилиндру, на поверхности которого отыскивается распределение тока. Индекс р будет относиться к цилиндру, который является источником для q-го цилиндра (p=-q при q=±
1).Для решения уравнения (9) преобразуем входящие в него функции Макдональда к виду:
|
(10) |
при
.
Кроме того, искомую функцию плотности тока второго приближения разложим в ряд Фурье
|
(11) |
Подставляя (10) и (11) в уравнение (9) и произведя несложные преобразования, можно записать выражение для плотности тока второго порядка рассеяния на q-ом цилиндре:
|
(12) |
где
Величину 
назовем коэффициентом рассеяния
второго порядка на q-ом цилиндре
|
(13) |
Здесь
- коэффициент рассеяния 1-го порядка
для р-го цилиндра.
Следуя изложенной схеме решения, можно получить выражение для плотности тока 3-го порядка рассеяния на q-ом цилиндре
|
(14) |
где  |
(15) |
- коэффициент 3-го порядка рассеяния
на q-ом цилиндре.
Принимая во внимание выражения (12) и (15), можно записать формулу для плотности тока v-го порядка рассеяния на q-ом цилиндре
|
(16) |
Здесь
=1 при нечетном v, и = 
при четном v (
при 
).
Рекуррентное соотношение для коэффициента рассеяния
v-го порядка имеет следующий вид:
|
(17) |
Рассмотрим интеграл, входящий в выражение (17). В подынтегральное выражение входят функции rr и y r , относящиеся к р-ой локальной координатной системе, которые являются функциями угла y q, относящиеся к q-ой координатной системе (рис. 1). Для вычисления этого интеграла необходимо получить формулы, позволяющие выразить цилиндрические функции, записанные в р-ой системе координат, через те же волновые функции, но в другой q-ой системе координат (р? q). Данный вопрос относительно функций Бесселя 1-го и 3-го рода рассмотрен подробно в [2]. Используя результаты указанной работы, нетрудно получить необходимый вид теоремы сложения для модифицированных функций Бесселя и в конечном счете более простое выражение для рекуррентной формулы коэффициента рассеяния
v - го порядка:
|
(18) |
Здесь использовано свойство четности по индексу модифицированных функций Бесселя.
Для определения величин R и q r (р=± 1) нетрудно получить следующие формулы
если
, то 
если
, то 
Закон распределения плотности тока, индуцированного на поверхности q-го цилиндра плоской
TM-волной и вторичными волнами всех порядков рассеяния р-го цилиндра, будет определяться выражением:
|
(19) |
Полный ток, текущий по поверхности q-го цилиндра, равен:
|
(20) |
3. Вектор-потенциал и составляющие электромагнитного поля системы цилиндров
Зная распределение токов индукции на цилиндрах, можно найти потенциал вторичного поля v-го порядка рассеяния для q-го цилиндра в каждом слое среды. Для практических целей наибольший интерес представляет вторичное поле системы взаимодействующих цилиндров в верхнем слое (воздухе). Чтобы найти потенциал q-го цилиндра в верхнем слое среды,
необходимо обратиться к решению вспомогательной задачи о поле линейного переменного тока в трехслойной среде [1, 9]. Используя выражения, полученные в этих работах, можно записать потенциал v-го порядка рассеяния для q - го цилиндра в виде:
|
(21) |
(
)
Подставив в (21) значения функций из формул [10] и [16] и проведя несложные преобразования, получим
|
(22) |
()
Здесь
.
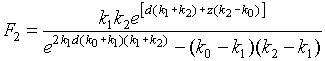Функция F
2 приближенно учитывает влияние границ раздела.В верхнем слое (j=0) потенциал вторичного поля
v-го приближения системы двух цилиндров будет равен:
|
(23) |
Прежде, чем перейти к получению выражений для составляющих рассеянных полей, целесообразно ввести новые обозначения для коэффициентов рассеяния, не содержащие компенсируемых сомножителей
|
(24) |
|
(25) |
Принимая во внимание новые обозначения коэффициентов рассеяния, приведем выражение (22) к виду:
|
(26) |
()
Для удобства вычислений сведем ряд в
(26) к сумме от «0» до 
. Так как модифицированные функции
Бесселя являются четными функциями относительно
целочисленного индекса, то преобразование ряда
(26) не вызывает затруднений. Используя результаты
преобразований, получим следующую формулу для
потенциала
|
(27) |
()
При этом, рекуррентное соотношение для коэффициентов рассеяния запишется
|
(28) |
где
|
(29) |
(p= -q, q= ± 1) |
Интеграл в (29) вычислен путем разложения подынтегральной функции в ряд и с применением теоремы о почленном интегрирования рядов [10]
|
Компоненты полного вторичного электромагнитного поля взаимодействующих цилиндров в любом слое среды могут быть определены через векторный потенциал при помощи известных соотношений:
|
||
|
(30) |
|
|
(j=0,1,2) |
Используя полученное выражение для вектор-потенциала (26), найдем компоненты поля в верхнем слое:
|
(31) |
|
(32) |
|
(33) |
В полученных выражениях коэффициенты рассеяния учитывают взаимодействие между цилиндрами, а функции Макдональда - характер рассеянного поля. Влияние плоских границ раздела на первичное и вторичное поле учитывается функцией F
2 и функциями F3(q), F4(q), которые приведены в работе [1].4. Результаты численных исследований
Результаты численных исследований структуры электромагнитного поля системы из двух цилиндров приведены на рис. 2- 9. Вид кривых на всех рисунках характеризует электромагнитное поле системы цилиндров в плоскости перпендикулярной оси цилиндра на высоте z от верхней границы раздела (рис. 1). По оси абсцисс отложено расстояние вдоль поверхности земли (у). Компоненты рассеянного поля рассчитывались в зависимости от расстояния между цилиндрами, радиусов цилиндров, глубины их залегания, частоты и электрических
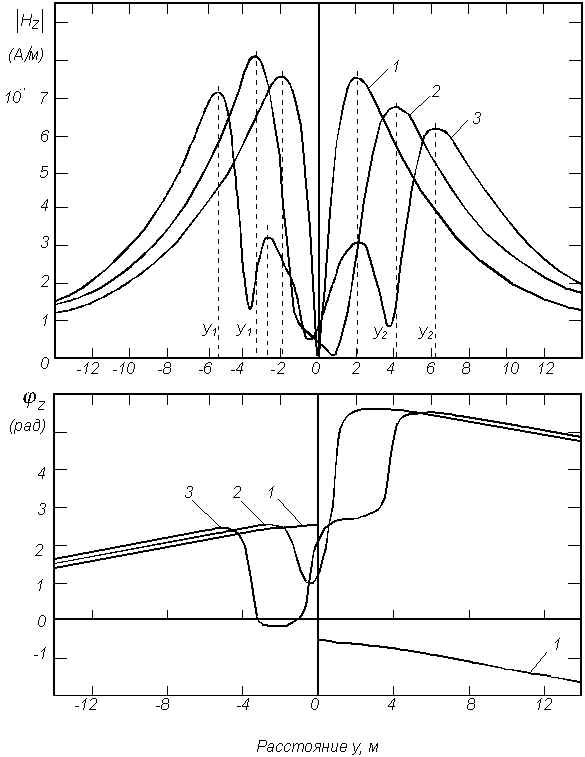
параметров среды.Поведение составляющих электромагнитного поля для системы цилиндров одинакового радиуса и расположенных на одной глубине при изменении расстояния между ними показано на рис. 2- 4. Сравнивая поведение компонент поля можно отметить, что более рельефны магнитные компоненты поля. По минимуму вертикальной составляющей магнитного поля во всех случаях четко прослеживается центр системы, что весьма важно в прикладном плане, в частности, для определения координат групповой подземной коммуникации. В этом же плане следует отметить, что разрешение системы с помощью |Hz| возможно лишь при
1,2h=1,2 (z+z1). При 
0.4h
координаты центра системы определяются так же,
как для одиночного цилиндра. Горизонтальная
составляющая поля Hy обладает более высокой
разрешающей способностью, чем Hz.
Фазовые кривые Yz над центром системы имеют скачок на "p ". С увеличением расстояния между цилиндрами
(
)
наблюдается сильное изменение фазы (близкое к
"p ") в области
соответствующей местоположению оси каждого
цилиндра, что говорит о возможности
использования фазовых измерений при определении
координат.
Исследование поведения составляющих поля для системы цилиндров разных радиусов и расположенных на различных глубинах при изменении расстояния между ними показали, что глубина залегания системы цилиндров, определяемая по местоположению максимума
|Hz|, находится в интервале между h1 и h2 (рис. 5). В случае, когда цилиндр меньшего радиуса расположен строго над цилиндром большего радиуса, центр системы определяется так же, как для одиночных тел.Области наибольшего градиента фазы вертикальной составляющей магнитного поля соответствует либо местоположению центра системы цилиндров (крив. 1 и 2 на рис. 5), либо местоположению каждого цилиндра в отдельности (крив. 3). Горизонтальная компонента магнитного поля обладает наиболее высокой разрешающей способностью.
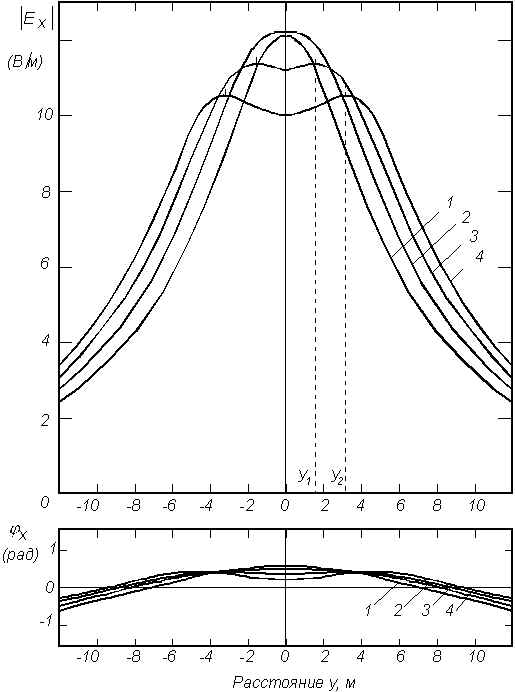
Электрическая компонента поля Ех обладает наименьшей разрешающей способностью как по фазе, так и амплитуде.
Исследования зависимости компонент поля системы цилиндров от изменения радиуса одного из них показали, что увеличение радиуса цилиндра не приводит к существенным изменениям поведения фазы составляющих. Для j
z области наибольших изменений фазы (близкие к "p ") соответствуют местоположению минимумов |Hz| (рис. 6). Фазовые кривые j y и j x почти повторяют поведение модулей составляющих. Амплитудные изменения |Hz| наиболее существенны (рис. 6).Повышение проводимости среды приводит к ослаблению взаимного влияния цилиндров, что объясняется возрастанием потерь в среде за счет вихревых токов. При этом амплитуды всех составляющих резко уменьшаются (рис. 7). В связи с укорочением длины волны в среде, фазовые кривые компонент делаются более рельефными. Улучшается дифференцируемость цилиндров в системе.
Исследование зависимости структуры поля системы цилиндров показывает, что с увеличением частоты амплитуда вертикальной составляющей магнитного поля уменьшается и ослабевает взаимное влияние полей цилиндров вследствие скин-эффекта (рис. 8). Повышается дифференцируемость системы и точность определения координат цилиндров. Области резких изменений фазы Hz характеризует местоположение осей цилиндров. Причем, более точно при повышении частоты (кривые 2- 3 рис. 8). С удалением от системы цилиндров фаза плавно меняется.
На рис. 9 показано поведение электрической составляющей Е
x. В отличие от магнитных составляющих данная компонента возрастает по амплитуде с увеличением частоты. Фазовые кривые электрической составляющей почти копирует ее поведение. Для них характерны более плавные изменения по сравнению с амплитудными.В Ы В О Д Ы
1. Предложена методика приближенного решения задачи дифракции плоской электромагнитной волны на двух проводящих круговых цилиндрах в плоскослоистой среде, представляющая собой сочетание методов криволинейных координат, функции линейного источника и возмущений.
2. На основе предложенной методики решена задача дифракции плоской волны на двух идеально проводящих бесконечно длинных круговых цилиндрах, расположенных в плоскослоистой среде. Конечные выражения представлены в виде двойных рядов по модифицированным функциям Бесселя.
3. На основе численных расчетов выполнен анализ структуры поля системы цилиндров в зависимости от расстояний между цилиндрами, их радиусов, электрических параметров среды и частоты.
4. Анализ структуры поля позволяет разработать методику определения координат системы из двух цилиндров, использующую те или другие компоненты электромагнитного поля.
5. В результате анализа показано, что повышение частоты зондирующего поля способствует дифференцируемости системы и улучшает точность определения координат цилиндров, что объясняется более сильным затуханием поля каждого цилиндра в среде в связи с явлением скин-эффекта и ослаблением их взаимного
влияния.Л И Т Е Р А Т У Р А
1. Семенов В.С., Неведомский А.В., Дыбовский В.Г. Возбуждение полем плоской электромагнитной волны проводящего цилиндра в слоистой земле. РАН, Радиоэлектроника, электронный журнал, 1999 г., № 2.
2. Иванов Е.А. Дифракция электромагнитных волн на двух телах. Минск, Наука и техника, 1968, 584 с.
3. Иванов Е.А., Мошинский А.В., Гельфонд В.С. К дифракции электромагнитных волн на двух эллиптических цилиндрах | АН БССР, сер. физ.-мат. н., 1969, № 4, С 5- 11.
4. Мошинский А.В. О рассеянии плоской ТМ-волны на двух параллельных произвольно ориентированных эллиптических цилиндрах, металлических лентах и их комбинациях. Изв. АН СССР, Радиотехника и электроника, 1970, т. 15, № 7, С. 1355-
1362.5. Howarth B.A. Multiple-Scattering resonances between parallel conducting cylinders. Can. J. Phys., 1973, 51, № 23, p. 2415- 2427.
6. Павлов А.Л. Дифракция на двух телах в локально-неоднородной среде. В сб. Вычислительные методы и программирование, МГУ, 1973, в. 20, С. 126-
133.7. Неведомский А.В. Дифракция плоской волны ТМ-типа на двух проводящих параллельных круговых цилиндрах в горизонтально-слоистой среде. Изв. вузов. Физика, 1980, № 1, С. 112.
8. Семенов В.С. Электромагнитное зондирование подстилающей поверхности и верхнего слоя грунта с целью их контроля и диагностики. Изв. вузов. Физика, 1988, № 8, С. 62-
75.9. Кулько В.Ф., Михайловский В.П. Электромагнитное поле в слоистых проводящих средах. Киев, Наукова думка, 1967, 142 с.
10. Воробьев Н.Н. Теория рядов. М., Наука,
1979.
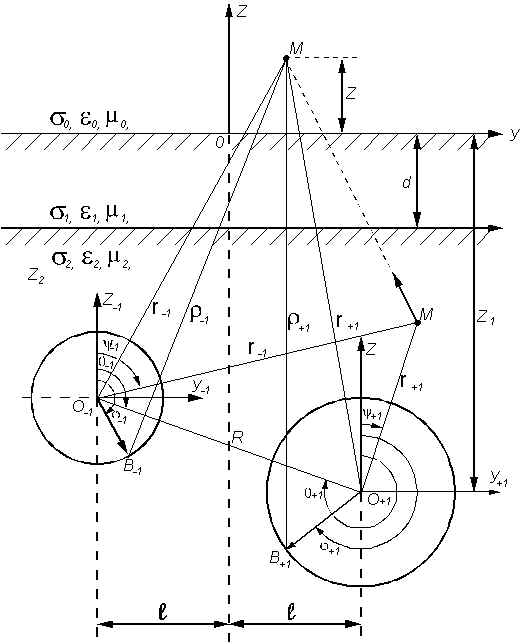
Рис. 1. Геометрия задачи.
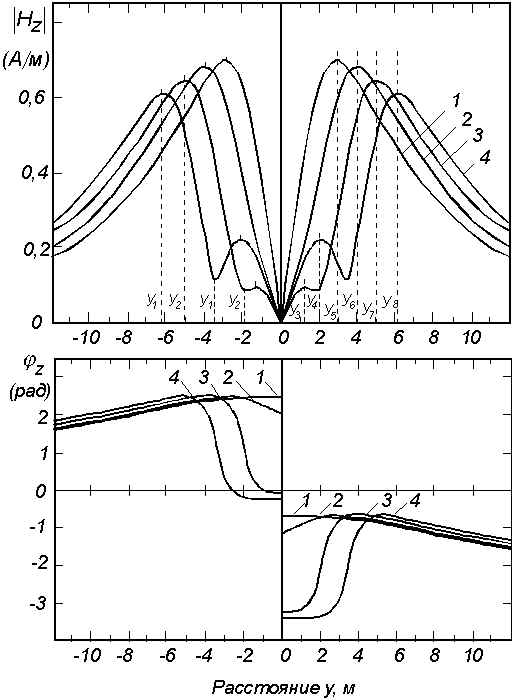
а+1=0,15м; а-1==0,15 м; z1,2=2,0 м; z=0,5м; d=1,0 м; f=0,3 МГц;
e 1=10; s 1=10-3
См/м; e 2=20; s 2=10-2 См/м1 – L=1,0
м; 2 – L=2,0 м; 3 – L=3,0 м; 4 – L=4,0 м;Рис. 2. Поведение вертикальной составляющей
магнитного поля системыдвух цилиндров одинакового радиуса при изменении расстояния между ними.
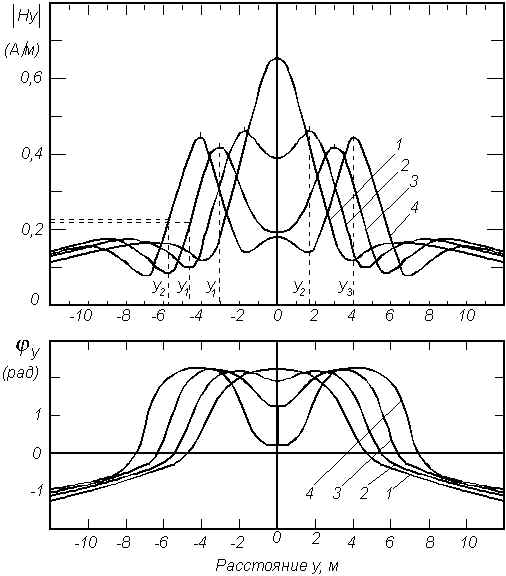
а
+1= а-1==0,15 м; z1,2=2,0 м; z=0,5 м; d=1,0 м; f=0,3 МГц;e 1=10; s 1=10-3
См/м; e 2=20; s 2=10-2 См/м1 – L=1,0
м; 2 – L=2,0 м; 3 – L=3,0 м; 4 – L=4,0 м;Рис. 3. Поведение горизонтальной составляющей
магнитного поля системыдвух цилиндров одинакового радиуса при изменении расстояния между ними.
а
+1= а-1==0,15 м; z1,2=2,0 м; z=0,5 м; d=1,0 м; f=0,3 МГц;e 1=10; s 1=10-3
См/м; e 2=20; s 2=10-2 См/м1 – L=1,0
м; 2 – L=2,0 м; 3 – L=3,0 м; 4 – L=4,0 м;Рис. 4. Поведение электрической составляющей
поля системыцилиндров одинакового радиуса при изменении расстояния между ними.
а
+1=0,2 м; а-1=0,025м; z1=2,0 м; z2=1,05 м;z=0,5
м; d=0,9 м; f=0,3 МГц;;e 1=10; s 1=10-3
См/м; e 2=20; s 2=10-2 См/м1 – L=1,0
м; 2 – L=2,0 м; 3 – L=4,0 м;Рис.
5. Поведение вертикальной составляющей магнитного поля системыдвух цилиндров одинакового радиуса при изменении расстояния между ними.
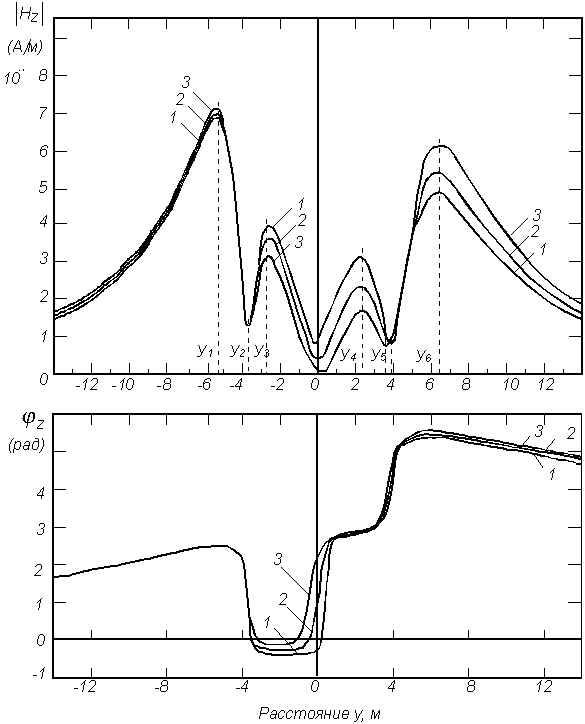
а
-1=0,025м; z1=2,0 м; z2=1,05 м; z=0,5 м; d=0,9 м;f=0,3
МГц; L=4,0 м;e 1=10; s 1=10-3
См/м; e 2=20; s 2=10-2 См/м1 –
а+1=0,05 м; 2 – а+1=0,1 м; 3 – а+1=0,2 м;Рис.
6. Зависимость вертикальной составляющей магнитного поля системыдвух цилиндров от изменения радиуса одного из них.
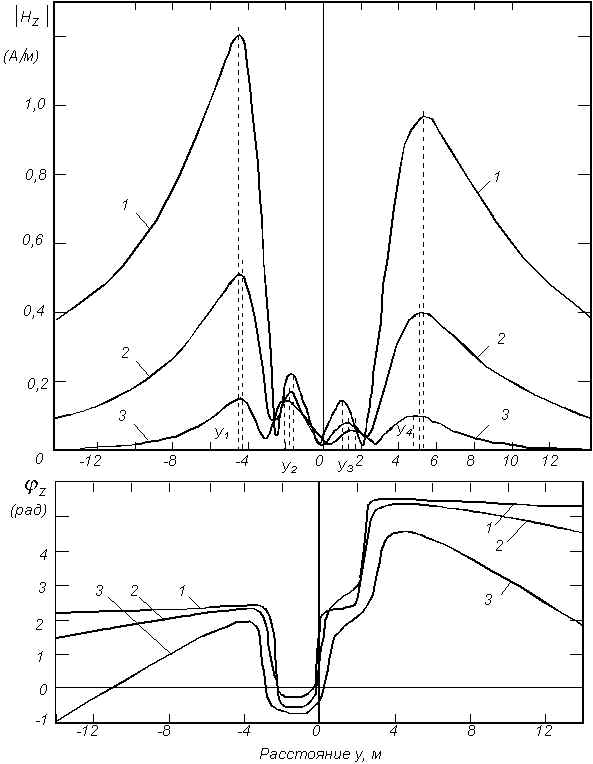
1 e 1,2=10; s 1,2=10-3 См/м; a+1=0,2 м; a-1=0,05 м; z1=2,0 м;
2 e 1,2=20; s 1,2=10-2 См/м; z2=1,05 м; z=0,5 м; d=0,9 м;
3 e 1,2=30; s 1,2=10-1 См/м; L=3,0 м; f=0,3 МГц
Рис. 7. Влияние электрических параметров среды на поведение вертикальной составляющей магнитного поля системы цилиндров.
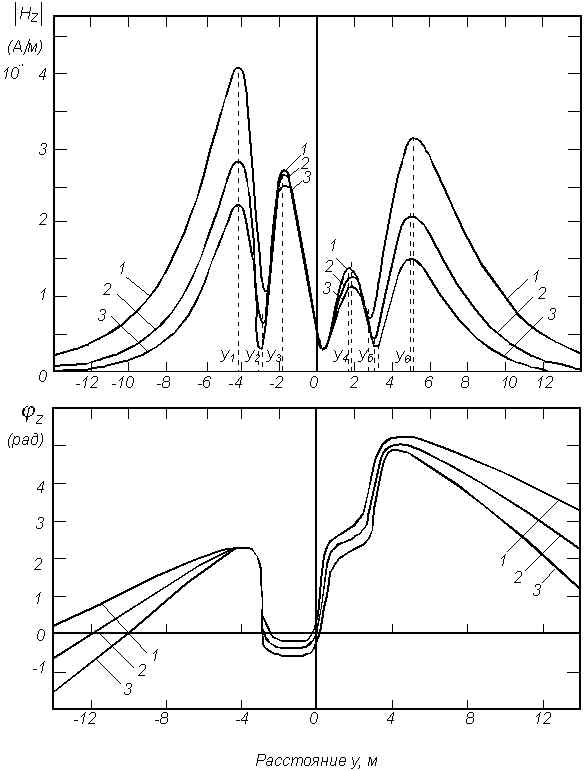
a+1=0,2 м; a-1=0,05 м; z1=2,0 м; z2=1,05 м; z=0,5 м; d=0,9 м;
L=3,0 м; e 1=20; s 1=10-2 См/м; e 2=30; s 2=10-1 См/м;
1 - f=0,15 МГц; 2 - f=0,3 МГц; 3 - f=0,5 МГц;
Рис. 8. Частотная зависимость вертикальной составляющей магнитного поля системы двух цилиндров.
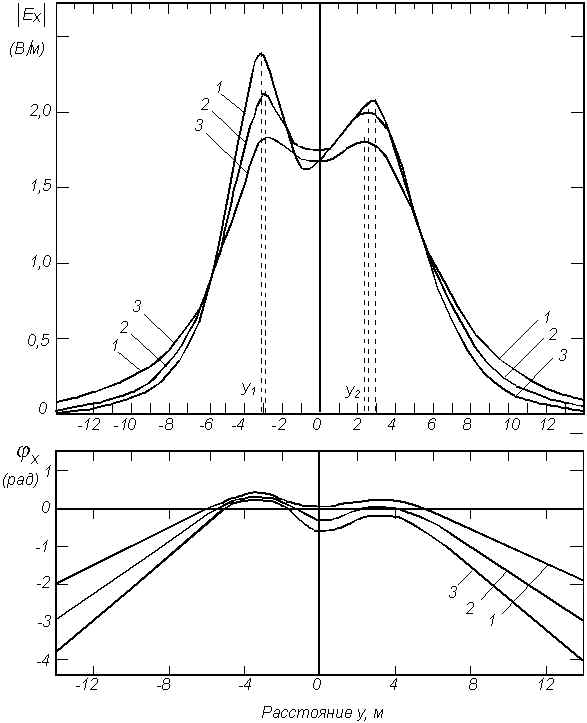
a+1=0,2
м; a-1=0,05 м; z1=2,0 м; z2=1,05 м; z=0,5 м; d=0,9 м;
L=3,0 м; e 1=20; s 1=10-2 См/м; e 2=30; s 2=10-1 См/м;
1- f=0,15
МГц; 2 - f=0,3 МГц; 3 - f=0,5 МГц;
Рис. 9. Частотная зависимость электрической составляющей поля системы двух цилиндров.
Авторы:
Семенов В.С.
- д. т. н., профессор, зав. отд. СФТИНеведомский А.В. - к. т. н., ст. н. с. СФТИ
Дыбовский Виктор Геннадьевич - к. ф.-м. н., ст. н. с. СФТИ,
e-mail: dybovsky@ic.tsu.ru |
 |
,
