| "ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" N 11, 2000 |
SMART ANTENNA BASE STATION BEAMFORMER FOR MOBILE COMMUNICATIONS
V. Zaharov,
F. Casco, O. Amin
Departamento de Ingeniería Eléctrica,
Universidad Autónoma Metropolitana
- Iztapalapa
México D.F., México
| "ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" N 11, 2000 |
SMART ANTENNA BASE STATION BEAMFORMER FOR MOBILE COMMUNICATIONS
V. Zaharov,
F. Casco, O. Amin
Departamento de Ingeniería Eléctrica,
Universidad Autónoma Metropolitana
- Iztapalapa
México D.F., México
Received November 13, 2000
A
novel RLS beamforming algorithm with low complexity and high accuracy for
applying in mobile communications smart antenna array processor is presented.
The proposed pipelined structure has a higher performing that conventional RLS
algorithm because require only vector
operation and can be easy implemented en VLSI. As result proposed pipelined
architecture can operate en N/k times
faster than conventional RLS structure, where N
and k are numbers of antenna elements
and training samples respectively, and more, this algorithm have a minimum
variance problem in finite precision implementation because one use
the Householder transform procedure of weight vector updating.
The technology of smart antennas for mobile
communications systems has received widely interest in the last couple of years
[1],[2],[3]. The principle
reason for applying smart antennas is the possibility for a large increase in
capacity due to control and reduce interferences. This is accomplish through the
use of narrow beams at the base site and as result
the users separations at the space.
A smart antenna combines antenna array with digital signal processing unit that optimize reception and radiation patterns dynamically in response to the signal environment, e.i. mobile moving about the coverage area. It is obvious that a smart antenna base station system is much more complex that traditional omnidirectional one because must include very powerful numeric processors and beamforming control systems.
In acordens with
[4] digital processor
is structured in four main sections
1.
Direction of arrival (DOA) estimation. From the received input data in
uplink the number of incoming wavefronts and their DOAs is estimated.
2.
DOA classification. In a next step are identified those wavefronts that
are originated from the user: First, the spatially resolved wavefronts, each
incident from an estimated DOA extract
from the input data, with a spatial pre-filter. Then, a user identification
decides whether a wavefront (DOA) belongs to a user or to an interfere.
3.
Tracking. The user DOAs are tracked to increase the reliability of the DOA
estimates.
4.
Signal reconstruction - beamforming.
Finally a beamforming algorithm forms an antenna pattern with a main beam
steered into the direction of the user, while minimizing the influence of the
interfering wavefronts.
The weights of
beamforming algorithm can be optimized from two criteria: maximization of
received signal from the desired user or maximization of the SIR (MSIR) by
suppressing the signal from interference sources. In case of SIR maximization is
to be used, the optimum weight vector Wopt
is given by
where R
is N´N correlation
matrix of the total received signal, P
is cross -
correlation vector between input vector and
desirable signal.
Even with the powerful signal processor available
today it is a very challenging task to perform
eq.(1) in real time because the computational
complexity of this operation sufficiently large and depends of number of antenna elements and applied algorithm category. There will
be a growing need for development of efficient algorithms for real time weights
optimizing and signal tracking.
In this paper we propose economically vector operations RLS algorithm for beamforming and tracking which allows decrease complexity of smart antenna base station. We present the architecture of proposed algorithm and comparison of computational complexity with conventional RLS algorithm.
We will consider the block diagram of the beamformer as shown at figure1.
Figure 1. Block diagram of the beamformer
The signal at the input of L antenna elements is
given
where
![]() is signal from i-th user which
satisfy the "narrowband assumption",
is signal from i-th user which
satisfy the "narrowband assumption",
![]() ,
,
![]() is angle of i-th user arrival
signal,
is angle of i-th user arrival
signal,
![]() are element space and wave length respectively, n(t)
is zero-mean thermal noise present in the receiver, M
is number of users.
are element space and wave length respectively, n(t)
is zero-mean thermal noise present in the receiver, M
is number of users.
Matrix of beamforming presents
as N row of the steering vectors
where
![]() ,
,
![]() ,
,
![]() is i-th reference angle.
is i-th reference angle.
The output signal of the Batler
matrix is
And the output signal of the i-th user beamformer is given
by
The recursive adaptive beamforming algorithm takes the general form
where
![]() is vector which minimize the mean
square error (MSE) between a reference signal
ak
and its linear estimation
is vector which minimize the mean
square error (MSE) between a reference signal
ak
and its linear estimation
![]() based on an observed input
vector of k-th sample time
based on an observed input
vector of k-th sample time
![]() , correlated with ak ,
, correlated with ak ,
![]() , T,H
are signs of transpose and
conjugate transpose accordingly.
, T,H
are signs of transpose and
conjugate transpose accordingly.
In this case for
MSE and MSIR criterions the optimal vector Wopt
is given by the same form [5]
where
![]()
When one used finite sample size
then formula (7) can be rewritten as
where
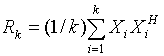 ,
,
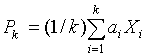 .
.
The increment
![]() depends on the algorithm.
The popular least mean square (LMS) algorithm has a form
depends on the algorithm.
The popular least mean square (LMS) algorithm has a form
This algorithm has good
performers but when covariance matrix
![]() has large eigenvalue spread, LMS
algorithm has a rather slow convergence[5].
The situation are changed if one should use in the increment
has large eigenvalue spread, LMS
algorithm has a rather slow convergence[5].
The situation are changed if one should use in the increment
![]() a inverse sampling matrix
a inverse sampling matrix
![]() which is close to
which is close to
![]() . In this case is obtained recursive least square algorithm (RLS) and least
square solution
. In this case is obtained recursive least square algorithm (RLS) and least
square solution
The
convergence rate of this algorithm more fast and not depends of eigenvalue
spreading, but the computational complexity of this algorithm is large. Consider
RLS algorithm given by one rank matrix modification formula
where m
is forgetting factor,
![]() . It is well known that
. It is well known that
![]() is computed without matrix division
using the matrix inversion lemma.
is computed without matrix division
using the matrix inversion lemma.
This updating algorithm (12)
requires
![]() complex multiplication per one
iteration because the base operation is multiplication of matrix on vector with
dimension N
and high sensitivity to computational errors.
complex multiplication per one
iteration because the base operation is multiplication of matrix on vector with
dimension N
and high sensitivity to computational errors.
where X
is matrix N´k
consisted from k input vectors, and
matrix T is a k´k
square matrix
![]() .
.
In (11) make a
substitution
![]() and given
and given
According to matrix inversion lemma
If
![]() then
then
We may rewrite eq.(15) as
where
Matrix A
may be present as
L
-
factorization
where L and
![]() are (k´
k)
lower and upper triangular matrixes accordingly. Omitting scale factor
are (k´
k)
lower and upper triangular matrixes accordingly. Omitting scale factor
![]() in
eq.(17) we get
in
eq.(17) we get
where
![]() is matrix N´k
which can be obtain solving system
is matrix N´k
which can be obtain solving system
Using eq.(8) and eq.(20) the optimal vector can be obtained in form
4. RECURSIVE PERFORMENS OF WEIGHT VECTOR
If input data are a sliding windows with N elements then matrix X for the m-th window has a structure
where
![]() .
.
Matrix
![]() for the (m+1)-th
window can be obtain as
for the (m+1)-th
window can be obtain as
where
![]() -
matrix
-
matrix
![]() without 1-th
column,
without 1-th
column,
![]() .
.
In this case matrix A from eq.(18) has the following structure (here shown only lower triangular part and diagonal for k=3 because matrix A is eremite and upper part will be conjugated
As follows from eq. (25)
From the matrix
![]() can be obtained recursively the
matrix
can be obtained recursively the
matrix
![]() (see part 5).
(see part 5).
Its easy that matrix
![]() has a following structure
has a following structure
where
![]() is k-th
row of matrix
is k-th
row of matrix
![]() .
.
![]() is matriz
is matriz
![]() without 1th
column. Solving the system of
linear eq. (21) we obtain
the vector
without 1th
column. Solving the system of
linear eq. (21) we obtain
the vector
![]() , j=1,2,...,k
, j=1,2,...,k
Using eq. (8),(22) and eq.(29) we have
following recursion for updating the value of adaptive vectors Wj, j = 1,2,…,k
.
5. RECURSIVE UPDATING OF MATRIX
![]() .
.
The matrixes
![]() and
and
![]() can be obtain using Cholesky
factorization [6].Then the elements of matrix
can be obtain using Cholesky
factorization [6].Then the elements of matrix
![]() is defined by
is defined by
How follows from eq.(28)
for matrix
![]() no need
calculate all elements but only for i=k,
becouse other elements was calculated at privies matrix
no need
calculate all elements but only for i=k,
becouse other elements was calculated at privies matrix
![]() . The elements of k-th row
could be calculate as
. The elements of k-th row
could be calculate as
However in case of obtaining
matrix
![]() using Choletsky
factorization improvement of
numerical stability is insignificant and the matrix R
should be formed in an obvious form (i.e. it
requires additional memory). Then must be made it
factorization that requires also additional
computational complexity.
using Choletsky
factorization improvement of
numerical stability is insignificant and the matrix R
should be formed in an obvious form (i.e. it
requires additional memory). Then must be made it
factorization that requires also additional
computational complexity.
The proposed algorithm allows to make recursive updating of vector W no form a matrix R in an obvious form but elements of a matrix L to receive directly from a matrix of input data X using Householder transform [7]. In this case the algorithm will have a minimum variance problem in finite precision implementation because the Householder transform has a big immunity against the computational errors [8].
Let us consider recursive
procedure of updating of elements of a matrix
![]() with
Householder transform application. We assume,
that the matrix X is presented as
with
Householder transform application. We assume,
that the matrix X is presented as
so that
![]() . Then
. Then
where Q -
(N+k)´
(N+k)
orthogonal Householder matrix. From eq.(34)
follows, that the elements of a matrix
![]() can
be received using orthogonal transformation above a matrix X,
not forming in an obvious form of a matrix A.
can
be received using orthogonal transformation above a matrix X,
not forming in an obvious form of a matrix A.
We present a matrix Q in factorized
form as
![]() . Then eq.(34) can be
rewrite as
. Then eq.(34) can be
rewrite as
where![]() ,
,
![]() ,
,
i=1,2...,
k, thus column![]() , j=1,2...,k
of matrix
, j=1,2...,k
of matrix![]() have passed the orthogonalization by matrixes Q1, Q2..., Qi-1
(i-1)
times. The matrixes Qi
according to [7] are determined as follows
have passed the orthogonalization by matrixes Q1, Q2..., Qi-1
(i-1)
times. The matrixes Qi
according to [7] are determined as follows
where
![]() is
(N+k)´
(N+k)
identity matrix. In eq.(36)
scalar Ci
is determined as follows
is
(N+k)´
(N+k)
identity matrix. In eq.(36)
scalar Ci
is determined as follows
where
![]() is i-th
column of a matrix
is i-th
column of a matrix ![]() .
The column vector Ui in eq.(36)
has dimension N+k and is determined by
expression
.
The column vector Ui in eq.(36)
has dimension N+k and is determined by
expression
where
 ,
,
![]() is the real part of an element
is the real part of an element
![]() ,
,
![]() is column-vector
which dimension same as a vector
is column-vector
which dimension same as a vector
![]() ,where unit is in
the
,where unit is in
the
i-th
place. The value ui
in (36) is i-th
element of a vector Ui.
Then i-th
step of column ortogonalization of a matrix
![]() will be
will be
We will present expression eq.(39)
with the account eq.(36) as
operations above vectors
With the account eq.(38)
we present eq.(40)
as
where
![]() ,
, 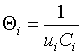 .
.
The expression eq.(41)
determines vector algorithm of reception of elements lij and
orthogonalization of vectors
![]() using Householder transform.
Proceeding from eq.(41)
we obtain expression for elements lij of a
matrix
using Householder transform.
Proceeding from eq.(41)
we obtain expression for elements lij of a
matrix
![]() as
as
where i = 1,2..., k,
j = i,i+1..., k.
Expression for
vectors orthogonalization yielding
Thus recursive computing process of reception of elements lij of a
matrix
![]() with use of Householder transform
on i-th
iteration (i = 1,2..., k) consists of
the following stages:
with use of Householder transform
on i-th
iteration (i = 1,2..., k) consists of
the following stages:
a)
Forming of a scalar Ci according
to expression (37);
b)
Forming of a vector Ui agrees eq.(38);
c)
The calculation lij
agrees eq.(42);
d)
Ortogonalization of vectors
![]() according to
eq.
(43).
according to
eq.
(43).
The
computational steps of adaptive weighting modifications algorithm could be
presented as follows
|
1. Inicialization
W0 =1,.
R0 = IN, Z0 = X1 for i=1,2,3,… for j=1,2,…k 2. Compute of triangular decomposition elements 2.1. Choletsky factorization 1. a) Obtain of i-th row of matrix A (eq.26) b) Obtain of i-th row of matrix L (eq.32) 2.2. Householder transform a)Obtain of i-th row of matrix L (eq.42) 3. Calculate of vector Z elements
4. Update of adaptive vectors elements Wj, |
Figure 2. The
architecture of the tracking algorithm
Figure
2 illustrates the architecture of the proposed algorithm and its computational
complexity in terms of multiplications and adders. As it can be observed from
the figure 3 the number of operations on the each stage no more than N
and total computational complexity equal 3N+k multiplicationes and adders
per one iteration. It means that
pipelined architecture will operate N/k
times faster then conventional structure.
Presented beamforming adaptive algorithm for computing the
optimum weight vector in accordance with MSIR criterion for mobile
communications smart antenna base station beamformer. The proposed algorithm can
be implemented with a linear complexity using only vector operations and
can be easy implemented en VLSI. Pipelined architecture can operate en N/k times faster than conventional RLS structure. The novel algorithm has a
minimum variance problem in finite precision implementation because one use in
the procedure of weight vector updating well known stable Householder transform
which has a big immunity against the computational errors.
8. REFERENCES
1. Liberti J.C., Rappaport T.S., Smart Antennas for Wireless Communications: IS-95 and Third-Generation CDMA Applications. Prentice Hall, NJ, 1999.
2. Barrett M., Arnott R. "Adaptive Antennas for Mobile Communications". Electronics and Communications Engineering Journal, Aug, 1994, pages 203214.
3. Winters J.H. “Smart antennas for wireless
systems". IEEE Personal Com.
Magazine, pages 23 -27, Feb, 1998.
4. Kuchar A. at all “Real-time smart antenna processing for GSM1800 base station” in IEEE Vehicular Technology Conference '99, Houston, Texas.
5. Haykin S. ”Adaptive Filter Theory”, Prentice Hall, NJ, 1996.
6. Golub G.H., Van Loan C. F. ”Matrix Computations”. 2nd edition, The Johns Hop-kins University
Press, North Oxford Academic
Publishing Co., Baltimore and London, 1989.
7. Householder A.S. “A class of method for inverting matrices”.J. Sos. Indust. Appl. Math, 1958, V.6, # 2, pages 189-195.
8. Wilkinson J..H. The algebraic eigenvalue problem: monographs in Numerical Analysis. Clarendon Press, Oxford, 1988.
Authors:
Zaharov Viktor
Vasilevich , Fausto Casco Sanches,
Omar Amin
vick@xanum.uam.mx,
Victor307@yahoo.com
Departamento de Ingeniería Eléctrica,
Universidad Autónoma Metropolitana
- Iztapalapa
México D.F., México