|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2002 |
|
СТАТИСТИЧЕСКИЙ АНАЛИЗ РАБОТЫ УМНОЖИТЕЛЕЙ ПЕРВИЧНОГО ФОТОЭЛЕКТРОННОГО ПОТОКА ФОТОЭМИССИОННЫХ ПРИБОРОВ
И.Е. Хайров, e-mail: snake2001@pisem.net
Таганрогский государственный радиотехнический университет, г. Таганрог.
Получена 10 ноября 2002 г.
Дается оценка эффективности работы умножителей первичного фотоэлектронного потока фотоэмиссионных приборов посредством статистического моделирования процесса умножения заряда в их динодной системе.
В качестве чувствительных элементов регистраторов сверхслабых оптических сигналов широкое применение получили одноэлектронные фотоэмиссионные приборы (ФЭП). Принцип работы этих устройств основан на электронном умножении первичного потока фотоэлектронов. В качестве умножителя в ФЭП, типа ФЭУ или диссектор, выступает динодная система, состоящая из Nд=5…15 каскадов умножения (динодов), а в ФЭП с микроканальными пластинами (МКП) - цилиндрические каналы, расположенные по всей поверхности пластины (системы с неразделенными динодами). Возможность умножения потока фотоэлектронов происходит тогда, когда число эмиттируемых поверхностью электронов превосходит число упавших. Поэтому поверхности динодов ФЭУ и внутренние поверхности цилиндрических каналов МКП покрыты материалами, обладающими значительной вторичной электронной эмиссией [1].
Наличие внутреннего умножения заряда в ФЭП позволяет усилить полезный сигнал до уровня, значительно превосходящего внутренние шумы последующей схемы обработки. В то же время, процесс вторичного умножения носит случайный характер, что, в свою очередь, вносит неопределенность в параметры выходного процесса ФЭП.
Целью статьи является оценка эффективности работы одноэлектронного ФЭП посредством статистического моделирования процесса умножения заряда в их динодной системе.
При этом предполагается, что:
¾ при попадании на фотокатод ФЭП
с квантовой эффективностью h в среднем ![]() фотонов за время измерения tизм, количество фотоэлектронов (ФЭ) n на
его выходе подчиняется закону Пуассона
фотонов за время измерения tизм, количество фотоэлектронов (ФЭ) n на
его выходе подчиняется закону Пуассона
со средним ![]() ;
;
¾ эффективность сбора ФЭ первым динодом ФЭП, типа ФЭУ или диссектор, близка к единице;
¾ пролеты и потери вторичных электронов в динодной системе отсутствуют;
¾ прозрачность микроканальной пластины для ФЭП с неразделенными динодами принята равной 70 % [2].
1. Статистический анализ электронного умножения ФЭП
Число вторичных электронов k1 с выхода первого динода является случайной величиной с производящей функцией Fk1(l). Пусть каждый первичный электрон, сгенерированный предыдущим динодом, порождает km вторичных электронов на выходе последующего динода с производящей функцией Fkm(l). Так как процесс вторичной эмиссии не зависит от порождающего его первичного потока электронов, то производящая функция числа электронов с Nд динода определяется выражением [3]
В [3] предложена методика рекуррентного построения производящей функции распределения числа вторичных электронов на выходе умножительной системы ФЭП и получены первые моменты распределений коэффициентов вторичной электронной эмиссии при пуассоновском распределении km Nд-каскадного умножителя без пролетов и потерь. При этом математическое ожидание M{k} и дисперсия D{k} записываются в следующем виде
Из (3) и (4) следует, что дисперсия числа вторичных электронов с выхода умножительной системы ФЭП пропорциональна его математическому ожиданию M{k}. В то же время флуктуации вторичного потока электронов имеют более высокую дисперсию, чем пуассоновское распределение с тем же средним M{k}.
Математическое ожидание числа вторичных электронов с выхода умножительной системы ФЭП определяется произведением коэффициентов вторичной эмиссии динодов и не зависит от последовательности расположения последних. Напротив, дисперсия числа вторичных электронов определяется как значением коэффициентов вторичной эмиссии динодов, так и последовательностью их соединения [3].
Действительно, если k1=5 и k2=3, то D{k}=60. При k1=3 и k2=5 имеем уже D{k}=90, т.е. дисперсия увеличилась в 1,5 раза при неизменности математического ожидания M{k}=15. Следовательно, для снижения мультипликативной составляющей шума умножения заряда целесообразно обеспечить высокий коэффициент вторичной электронной эмиссии k 1 с первого динода ФЭП [3].
2. Статистический анализ электронного умножения ФЭУ и диссекторов
Одноэлектронные ФЭУ и диссекторы обычно имеют Nд=5…15 динодов в умножительной системе [1]. При этом коэффициент вторичной эмиссии первого, а чаще первого и второго динодов составляет 5…8, в то время как для последующих он равен трем [1].
Рассмотрим несколько наиболее часто встречающихся на практике вариантов построения динодных систем одноэлектронных ФЭП с Nд=14 каскадами умножения.
Вариант
I. Коэффициент вторичного умножения
первого динода ![]() , а последующих
, а последующих ![]() . При этом общий
коэффициент умножения заряда составляет
. При этом общий
коэффициент умножения заряда составляет 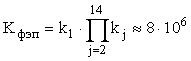 .
.
Отношение сигнала к шуму (С/Ш) умножительной системы первичного фотоэлектронного потока можно характеризовать величиной [3]
В табл. 1 сведены средние статистические характеристики числа вторичных электронов с выхода m-го динода (m=1, 2, …, 14). В колонках 2…4 даны результаты расчета параметров процесса по формулам (3)…(5), а в колонках 5…7 результаты полученные посредством статистического моделирования коэффициентов вторичной электронной эмиссии динодной системы ФЭП по закону Пуассона (1).
Средние статистические характеристики числа вторичных электронов с выхода m-го динода
|
Число динодов, Nд |
Расчет |
Моделирование |
||||
|
M{k} |
D{k}/M{k} |
qM |
M{k} |
D{k}/M{k} |
qM |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
5 |
1 |
5 |
4,98 |
1 |
4,98 |
|
2 |
15 |
4 |
3,75 |
14,95 |
4,02 |
3,714 |
|
3 |
45 |
13 |
3,46154 |
44,74 |
12,96 |
3,451 |
|
4 |
135 |
40 |
3,37500 |
134,13 |
39,9 |
3,362 |
|
5 |
405 |
121 |
3,34711 |
400,58 |
119,47 |
3,353 |
|
6 |
1215 |
364 |
3,33791 |
1199,5 |
361,6 |
3,317 |
|
7 |
3645 |
1093 |
3,33486 |
3600 |
1091 |
3,298 |
|
8 |
10935 |
3280 |
3,33384 |
10780 |
3223 |
3,344 |
|
9 |
32805 |
9841 |
3,33350 |
32313 |
9693 |
3,334 |
|
10 |
98415 |
29524 |
3,33339 |
96840 |
29051 |
3,333 |
|
11 |
295245 |
88573 |
3,33335 |
290521 |
87067 |
3,337 |
|
12 |
885735 |
265720 |
3,33334 |
870677 |
260937 |
3,333 |
|
13 |
2,66×106 |
797161 |
3,33334 |
2,61×106 |
782795 |
3,333 |
|
14 |
7,97×106 |
2,39×106 |
3,33333 |
7,81×106 |
2,34×106 |
3,331 |
Генерация случайного
числа ![]() осуществляется
по алгоритму предложенному Каном [4] и предполагает образование произведений
равномерно распределенных последовательностей случайных чисел
осуществляется
по алгоритму предложенному Каном [4] и предполагает образование произведений
равномерно распределенных последовательностей случайных чисел ![]() . Количество
сомножителей выбирается таким, чтобы выполнялось неравенство
. Количество
сомножителей выбирается таким, чтобы выполнялось неравенство ![]() . При этом
число m-1 представляет собой искомую случайную переменную
. При этом
число m-1 представляет собой искомую случайную переменную ![]() , распределенную по
закону Пуассона со средним
, распределенную по
закону Пуассона со средним ![]() .
.
В процессе моделирования
процесса вторичной эмиссии произведен анализ предложенного Каном алгоритма
генерации случайной переменной ![]() , распределенной по закону Пуассона со
средним
, распределенной по закону Пуассона со
средним ![]() .
Сгенерированная, таким образом, последовательность случайных величин имеет
математическое ожидание и дисперсию, отличающиеся от
.
Сгенерированная, таким образом, последовательность случайных величин имеет
математическое ожидание и дисперсию, отличающиеся от ![]() , на сотые доли процента
[5]. Это подтверждает правомерность использования предлагаемого алгоритма
генерации случайных чисел по закону Пуассона (1).
, на сотые доли процента
[5]. Это подтверждает правомерность использования предлагаемого алгоритма
генерации случайных чисел по закону Пуассона (1).
Из табл. 1 видно, что численные значения средних статистических характеристик числа вторичных электронов, полученные моделированием, отличаются от теоретических, менее чем на 2,5 %. Это также подтверждает справедливость предложенной модели.
Рост числа динодов Nд снижает отношение С/Ш (см. табл. 1). Однако это снижение не значительно и при числе каскадов умножения равном 14, отличается от отношения С/Ш на выходе третьего динода всего на 3,8 %, а на выходе второго динода на 12,5 %. На практике это позволяет заменить расчет отношения С/Ш на выходе ФЭД с Nд каскадами умножения расчетом отношения С/Ш после второго динода
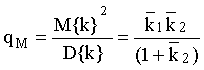 .
.
Вариант
II. Коэффициенты умножения первого и
второго динодов равны между собой и составляют ![]() , а последующих
, а последующих ![]() . При этом
общий коэффициент умножения заряда составляет
. При этом
общий коэффициент умножения заряда составляет 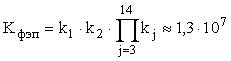 .
.
В табл. 2 сведены средние статистические характеристики числа вторичных электронов с выхода m-го динода (m=1, 2, …, 14).
Как и предыдущем случае в колонках 2…4 табл. 2 числовые значения параметров процесса умножения получены по формулам (3)…(5), а в колонках 5…7 ¾ статистическим моделированием коэффициентов вторичной электронной эмиссии по закону Пуассона (1).
Из табл. 2 видно, что отношение С/Ш на выходе 14-го динода отличается от отношения С/Ш на выходе третьего динода всего на 2,6 %, а на выходе второго динода на 8,3 %.
Средние статистические характеристики числа вторичных электронов с выхода m-го динода
|
Число динодов, Nд |
Расчет |
Моделирование |
||||
|
M{k} |
D{k}/M{k} |
qM |
M{k} |
D{k}/M{k} |
qM |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
5 |
1 |
5 |
4,98 |
1 |
4,98 |
|
2 |
25 |
6 |
4,167 |
24,83 |
6,01 |
4,13 |
|
3 |
75 |
19 |
3,94737 |
74,61 |
19,19 |
3,889 |
|
4 |
225 |
58 |
3,87931 |
222,47 |
57,23 |
3,887 |
|
5 |
675 |
175 |
3,85714 |
668,92 |
175,24 |
3,817 |
|
6 |
2025 |
526 |
3,84981 |
1999 |
523,3 |
3,819 |
|
7 |
6075 |
1579 |
3,84737 |
5991 |
1565 |
3,827 |
|
8 |
18225 |
4738 |
3,84656 |
17983 |
4700 |
3,826 |
|
9 |
54675 |
14215 |
3,84629 |
53909 |
14094 |
3,825 |
|
10 |
164025 |
42646 |
3,8462 |
161564 |
42228 |
3,826 |
|
11 |
492075 |
127939 |
3,84617 |
484694 |
126647 |
3,827 |
|
12 |
1,48×106 |
383818 |
3,84616 |
1,45×106 |
379160 |
3,831 |
|
13 |
4,43×106 |
1,15×106 |
3,84616 |
4,35×106 |
1,14×106 |
3,826 |
|
14 |
1,33×107 |
3,45×106 |
3,84615 |
1,3×107 |
3,41×106 |
3,824 |
Т.о., из полученных
результатов видно, что при коэффициенте вторичной электронной эмиссии первых
двух динодов равных ![]() уменьшение отношения С/Ш на выходе 14-го
динода, по сравнению со вторым динодом, будет в 1,5 раза меньше, чем в случае
коэффициента вторичной эмиссии равного
уменьшение отношения С/Ш на выходе 14-го
динода, по сравнению со вторым динодом, будет в 1,5 раза меньше, чем в случае
коэффициента вторичной эмиссии равного ![]() только для первого динода. При этом полагается,
что последующие диноды имеют коэффициент умножения равный трем.
только для первого динода. При этом полагается,
что последующие диноды имеют коэффициент умножения равный трем.
Так же важно отметить, что амплитудное значение одноэлектронного импульса тока на выходе ФЭП с динодной системой второго рассматриваемого варианта в 1,6 раза больше варианта I, при прочих равных условиях.
3. Статистический анализ электронного умножения в МКП
Как отмечалось выше, МКП
представляет собой электронные умножители с неразделенными динодами.
Конструктивно МКП ¾ это диск, изготовленный из свинцового стекла толщиной 0,5¸1 мм и диаметром до 60 мм, состоящий
из большого количества цилиндрических каналов (до 107) [2].
Внутренние поверхности микроканалов покрыты высокоомным полупроводниковым
слоем, имеющим коэффициент эмиссии вторичных электронов 1,2<![]() <2,5. При каскадном умножении
коэффициент усиления МКП определяется выражением
<2,5. При каскадном умножении
коэффициент усиления МКП определяется выражением ![]() , где n ¾ число каскадов усиления. При этом видно, что при
среднем коэффициенте эмиссии
, где n ¾ число каскадов усиления. При этом видно, что при
среднем коэффициенте эмиссии ![]() для достижения коэффициента усиления всей
МКП Kфэп=106 потребуется
для достижения коэффициента усиления всей
МКП Kфэп=106 потребуется ![]() каскадов умножения (количество
соударений вторичных электронов о внутренние стенки микроканалов). Такой
большой коэффициент усиления K=106…107
достигается при шевронном включении нескольких МКП [2].
каскадов умножения (количество
соударений вторичных электронов о внутренние стенки микроканалов). Такой
большой коэффициент усиления K=106…107
достигается при шевронном включении нескольких МКП [2].
Рассмотрим случай применения
МКП шевронного типа, в которой средний коэффициент вторичной эмиссии при одном
соударении электронов с внутренней поверхностью микроканала составляет ![]() .
.
В табл. 3 сведены средние статистические характеристики числа вторичных электронов с выхода m-го каскада усиления (m=1, 2, …, 20).
Здесь в колонках 2…4 численные значения параметров процесса умножения получены по выражениям (3)…(5), а в колонках 5…7 ¾ статистическим моделированием коэффициентов вторичной эмиссии по закону Пуассона (1).
Средние статистические характеристики числа вторичных электронов после m-го соударения
|
|
Количество соударений, m |
Расчет |
Моделирование |
|||||||||||
|
|
M{k} |
D{k}/M{k} |
qM |
M{k} |
D{k}/M{k} |
qM |
||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||
|
1 |
2 |
1 |
2 |
1,99 |
1 |
1,99 |
|
|||||||
|
2 |
4 |
3 |
1,33333 |
3,98 |
3,01 |
1,323 |
|
|||||||
|
3 |
8 |
7 |
1,14286 |
7,98 |
6,98 |
1,143 |
|
|||||||
|
4 |
16 |
15 |
1,06667 |
15,81 |
14,96 |
1,057 |
|
|||||||
|
5 |
32 |
31 |
1,03226 |
31,73 |
30,77 |
1,031 |
|
|||||||
|
6 |
64 |
63 |
1,01587 |
63,4 |
62,37 |
1,016 |
|
|||||||
|
7 |
128 |
127 |
1,00787 |
126,05 |
125,23 |
1,007 |
|
|||||||
|
8 |
256 |
255 |
1,00392 |
250,12 |
252,1 |
1,992 |
|
|||||||
|
9 |
512 |
511 |
1,00196 |
504,6 |
504 |
1,001 |
|
|||||||
|
10 |
1024 |
1023 |
1,00098 |
1011 |
1005 |
1,006 |
|
|||||||
|
11 |
2048 |
2047 |
1,00049 |
2019 |
2012 |
1,004 |
|
|||||||
|
12 |
4096 |
4095 |
1,00024 |
4039 |
4036 |
1,001 |
|
|||||||
|
13 |
8192 |
8191 |
1,00012 |
8069 |
8059 |
1,001 |
|
|||||||
|
14 |
16384 |
16383 |
1,00006 |
16138 |
16124 |
1,001 |
|
|||||||
|
15 |
32768 |
32767 |
1,00003 |
32243 |
32229 |
1 |
|
|||||||
|
16 |
65536 |
65535 |
1,00002 |
64487 |
65001 |
0,992 |
|
|||||||
|
17 |
131072 |
131071 |
1 |
128843 |
128795 |
1 |
|
|||||||
|
18 |
262144 |
262143 |
1 |
257687 |
258075 |
0,998 |
|
|||||||
|
19 |
524288 |
524287 |
1 |
514850 |
514758 |
1 |
|
|||||||
|
20 |
1048576 |
1048575 |
1 |
1029701 |
1034772 |
0,995 |
|
|||||||
Как отмечалось выше, для минимизации мультипликативной составляющей шума умножительной системы ФЭП и, соответственно, для повышения отношения С/Ш, необходимо увеличить коэффициент умножения первых каскадов, по сравнению с последующими. Как видно, МПК не удовлетворяет этому критерию. Действительно, и так при малом отношении С/Ш после первого каскада (равном 2), оно уже на выходе седьмого каскада уменьшается практически до единицы (см. табл. 3).
Сравнивая данные, полученные моделированием с теоретически полученными значениями (см. табл. 3) видно, что результаты отличаются не более чем на 2 %. Это подтверждает правомерность использования и справедливость предложенной модели.
Из табл. 3 видно, что отношение С/Ш на выходе двадцатого каскада умножения отличается от отношения С/Ш на выходе второго каскада более чем на 33 %, а на выходе третьего каскада на 14 % и только на выходе четвертого каскада оно отличается всего на 6,7 %. Поэтому, в отличие от предыдущих двух случаев, на практике отношение С/Ш на выходе n-го каскада умножения можно заменить расчетом отношения С/Ш как минимум после третьего каскада (или после четвертого)
 .
.
Сравнивая результаты
сведенные в табл. 1, 2 и 3 видно, что отношение С/Ш на выходе второго
каскада умножения в случае ![]() , а
, а ![]() в 2,8 раза, а при
в 2,8 раза, а при ![]() в 3,1 раза больше, чем
в случае при
в 3,1 раза больше, чем
в случае при ![]() .
.
Т.о., анализ результатов проведенных исследований показывает справедливость предложенной модели оценки средних статистических характеристик числа вторичных электронов. Подтверждено, что для уменьшения мультипликативной составляющей шума умножительной системы ФЭП и, соответственно, повышения отношения С/Ш, необходимо увеличивать коэффициент вторичной электронной эмиссии первых каскадов умножения, по сравнению с последующими. Установлено, что замена на практике расчета отношения С/Ш с выхода n каскадного умножителя расчетом отношения С/Ш после второго каскада справедлива лишь для умножителей с коэффициентом умножения первых двух каскадов (или только первого) превышающем коэффициент умножения последующих в 1,5¸2 раза. В случае равенства коэффициентов умножения всех каскадов, этот расчет может быть заменен расчетом отношения С/Ш только после третьего или четвертого каскадов (как в случае МКП).
1. Hartel V., Optoelectronics: theory and practice, McGraw Hill-Texas Instruments Electronics Series, N.Y., 1978.
2. Дмитриев В.Д., Лукьянов С.М. и др. Микроканальные пластины в экспериментальной физике. ПТЭ, 1977, №2. С. 7.
3. Щелкунов К.Н. Статистический анализ фотоэлектронных умножителей. Изв. вузов СССР. "Приборостроение". 1978. Т. 21, № 8, 10.
4. Мартин Ф. Моделирование на вычислительных машинах.¾ М.: Сов.радио, 1972.
5. Радиоэлектронные технологии информационной безопасности. Сборник научных статей Под ред. К.Е. Румянцева.¾ Таганрог: Издательство ТРТУ, 2002.¾ 286 с.
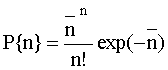 . (1)
. (1)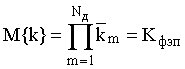 , (3)
, (3)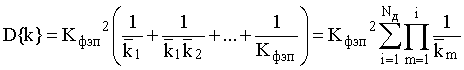 . (4)
. (4)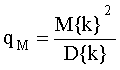 . (5)
. (5)