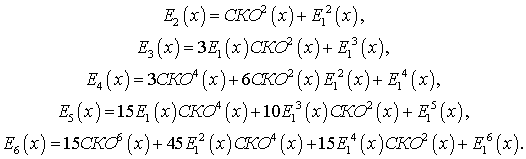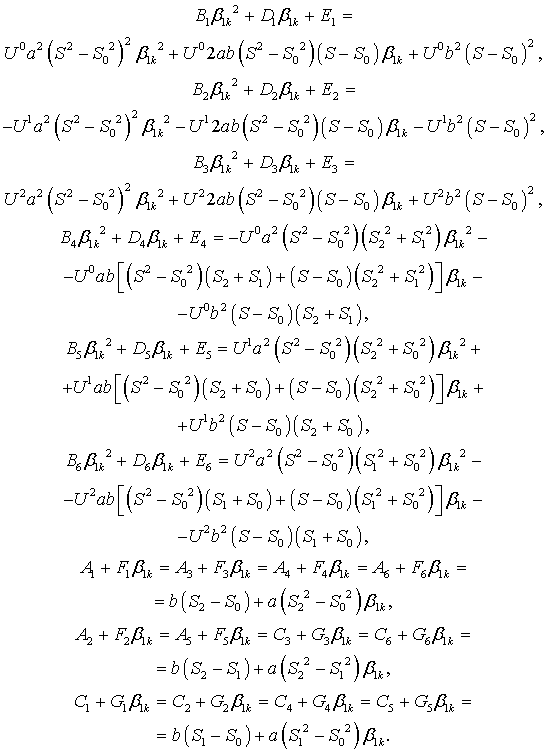Коррекция геометрического шума МФПУ с помощью аппроксимации методом наименьших квадратов передаточных характеристик матрицы полиномом T-го порядка

 

Д. С. Брондз, Е. Н. Харитонова

ФГУП «Особое конструкторско-технологическое бюро «Омега», Великий Новгород

Получена 28 октября 2008 г.

В настоящее время самым распространенным и наиболее эффективным среди используемых на практике методов коррекции геометрического  шума матричных фотоприемных устройств (МФПУ) является метод линейной, или двухточечной, коррекции. Двухточечная коррекция проводится из предположения, что зависимость выходного сигнала элементов матрицы от входного линейна. В действительности эта зависимость отличается от линейной в большей или меньшей степени для разных элементов. Поэтому полностью устранить неоднородность не удается. В результате исследования, целью  которого являлось повышение эффективности коррекции, сделан вывод, что эффективность можно повысить, во-первых, путем повышения порядка полинома, аппроксимирующего передаточные характеристики МФПУ, во-вторых, путем повышения количества точек аппроксимации и использования метода наименьших квадратов для нахождения коэффициентов коррекции. Для доказательства данного утверждения приводится теоретическая и практическая оценка эффективности различных методов коррекции для ПЗС-матрицы KAI-1003 фирмы «Kodak». Исследования показали, что применение  полинома второго порядка в системах автоматической обработки информации в качестве аппроксимирующей  функции обосновано с точки зрения оптимального отношения эффективности коррекции и количества требуемых вычислительных ресурсов.

 

Ключевые слова: регистрация изображений, обработка изображений, матричные фотоприемники.

1       Введение

Геометрический шум представляет собой фиксированные отклонения значения выходного сигнала разных каналов матричного фотоприемного устройства (МФПУ), вызванного одинаковым входным воздействием. Под каналом понимается участок системы, формирующий электрический сигнал, начиная с отдельного чувствительного элемента фотоприемника и кончая выходом матрицы.

Целью коррекции геометрического шума является получение от каждого пикселя МФПУ сигнала одного и того же уровня при условии их равномерной освещенности – коррекция плоского поля [9, 11, 21].

В настоящее время на практике применяют линейную коррекцию неравномерности чувствительности как аппаратно [14, 20], так и программно [1, 7, 12,  15, 23].

Как правило, полностью скомпенсировать влияние геометрического шума данным методом не удается. Причин этому может быть несколько: неоднородность облучения при калибровке, уход значений параметров приемников за время прошедшее после окончания последней калибровки и, основная причина [19], отклонение параметров реальных приемников от линейной модели.

Перед авторами стояла цель - усовершенствовать существующий метод коррекции геометрического шума с целью повышения качества изображения и достоверности расчетов при проектировании специализированных видеосистем на основе МФПУ.

Чтобы оценить и сравнить эффективность того или иного метода коррекции, определим геометрический шум как квадрат среднеквадратического отклонения (СКО) выходных сигналов МФПУ при условии равномерной засветки камеры.

Относительную эффективность коррекции определим как

,                    

где S_вых и S_вых‘ – выходные сигналы до и после коррекции.

Используемая в расчетах модель формирования выходного сигнала S_вых k-го канала МФПУ выражается следующей формулой:

,               

где  S – входной сигнал, β₁ – квантовая эффективность, s – случайная величина с математическим ожиданием E₁(s)=E₁(β_1k)*S и среднеквадратическим отклонением СКО(s)=СКО(β₁) *S, α₂ = α – сигнал, вызываемый темновым током, β₂ – функция интегральной чувствительности, которая аппроксимируется полиномом второго порядка с коэффициентами «a», «b» и «c».

Все расчеты будем делать для ПЗС-матриц, для которых, в отличие от КМОП-матриц, «a», «b» и «c» - константы, т.е. одинаковы для всех каналов.

2       Линейная коррекция

При линейной коррекции скорректированное значение яркости пикселя рассчитывается по формуле:

                                      

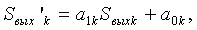
где a_1,0 -  коэффициенты коррекции, получаемые из системы уравнений:

                                          

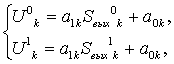
где U – эталонная яркость пикселя.

В качестве эталонного (истинного) значения яркости пикселя U в зависимости от алгоритма принимается либо значение какого-либо пикселя, либо среднее значение яркости, рассчитанное по кадру [2] или блоку пикселей, например по нескольким, соседним строкам [7, 8]. Значение U также может быть найдено гистограммным методом, как максимум ординаты на гистограмме яркости всего изображения [8, 23].

Значения с разными верхними индексами получены при разной интенсивности освещения. Обычно первое измерение делается при нулевом освещении, а второе измерение при освещении, при котором значение яркости элементов близко к максимальному, но не входит в насыщение.

Для матриц ИК-диапазона измерения делаются при разных значениях температуры [2, 7, 12], а не освещенности [3, 8, 18].

Так как измерения проводятся при двух значениях интенсивности освещения, такая линейная коррекция называется также двухточечной.

Двухточечная коррекция проводится из предположения, что зависимость выходного сигнала элементов матрицы от входного линейна. В действительности эта зависимость отличается от линейной в большей или меньшей степени для разных элементов. Поэтому полностью устранить неоднородность не удается.

Оценим эффективность линейной коррекции для ПЗС матрицы. Из формул , и получаем:

.

Чтобы упростить решение, не будем брать в расчет составляющую темнового тока. Учитывая, что s=β1k*S, получаем

.             

Дисперсия случайной величины «x» вычисляется по следующей формуле [16] :

.                               

где E₁ - математическое ожидание (МО), E₂ – второй начальный момент.

  Если эталонная яркость для всех пикселей одинаковая (рассчитывается как среднее по кадру), то

.       

Если рассматривается измеримая функция вида y=ψ(x) и непрерывная случайная величина ξ(ω) с плотностью распределения fξ(x), которые порождают случайную величину η(ξ(ω)), то математическое ожидание этой случайной величины рассчитывается по формуле [16]:

.                                      

Откуда

.         

Делаем замену. Случайная величина y=(S1+S0)*β1k+b/a имеет нормально распределение  с математическим ожиданием E1(y)=(S1+S0)*E1(β1)+b/a и среднеквадратическим отклонением СКО(y) =(S1+S0)*СКО(β1).

.   

. 

.   

. [5]                

Условие выполняется при

.                                           

Используя формулы , получаем

.    

 

Ряд в формуле сходится при условии E1(y)/СКО(y)<1, а при выполнении условия хорошо аппроксимируется суммой нескольких первых членов.

.         

.  [5]             

.

Ряд в формуле сходится при условии E1(y)/СКО(y)<1, а при выполнении условия хорошо аппроксимируется суммой первых трёх членов. Согласно

 

.

.             

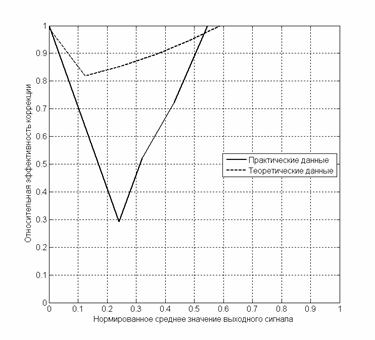
На рисунке 1 представлены графики, полученные по теоретическим и практическим данным для ПЗС-матрицы KAI-1003 фирмы «Kodak».

 

Рис.1 – Графики относительной эффективности коррекции геометрического шума методом двухточечной коррекции, полученные по практическим и теоретическим данным для ПЗС-матрицы KAI-1003.

3       Коррекция с помощью полинома T-го порядка

Для более точной коррекции естественно было бы применить уравнение более высокого порядка T:

.                                       

Некоторые исследования [19] показали, что среди источников остаточного шума после коррекции неравномерности чувствительности, таких как фотонный шум источника изображения, неравномерность освещенности при калибровке и нелинейности характеристик элементов матрицы, последний вносит наибольший вклад.

Но схемы коррекции, использующие уравнения белее высокого порядка, остаются теоретическими разработками [10, 15, 18, 22].

Дело в том, что с ростом порядка уравнения происходит рост требуемой вычислительной мощности и объем требуемой памяти. Необходима также более сложная методика расчета данных коэффициентов, чем для случая двухточечной коррекции.

Существующая на сегодняшний день элементная база позволяет хранить необходимый объем данных и обладает достаточной вычислительной мощностью, чтобы использовать алгоритмы коррекции геометрического шума, использующие уравнения коррекции второго и даже третьего порядка. 

Найдем оценку эффективности коррекции геометрического шума с помощью полинома 2-го порядка для ПЗС матрицы при условии α=0 и U=const, аналогичную тому, как это сделано для линейной коррекции. Т.к. в формуле c≈0, будем считать, что c=0.

Скорректированное значение яркости пикселя рассчитывается по формуле:

.                 

Для нахождения коэффициентов коррекции необходимо минимум три уравнения и, следовательно, три опорных точки, соответствующих эталонным яркостям:

                           

.

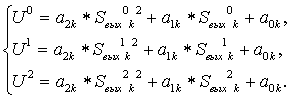
где

  Рассмотрим вспомогательный интеграл , где f – некоторая функция.

.[5]

Воспользуемся  формулой интегрирования по частям [5]

.

Согласно 

.    

 

.

Согласно  , ,

.

.         

Каждый интеграл в формулах и решается аналогично заменой уравнения в знаменателе на «y». Рассмотрим для примера один из интегралов.

Случайная величина y=Fi*β1k+Ai имеет нормально распределение  с математическим ожиданием E1(y)=Fi*E1(β1)+Ai и среднеквадратическим отклонением СКО(y) = Fi*СКО(β1).

Если Ai≠Aj и Fi≠Fj, то

.

  Каждый из интегралов в решается так:

 .

Если Ai=Aj и Fi=Fj, то

.

 

 

 

Рис.2 – Графики относительной эффективности коррекции геометрического шума с помощью полинома 2-го порядка по трем опорным точкам, полученные по практическим и теоретическим данным для ПЗС-матрицы KAI-1003.

4       Метод наименьших квадратов

Эффективность коррекции по формулам ( и  , и )  зависит от значения входного сигнала. Эффективность максимальна при значениях входного сигнала, соответствующих эталонным яркостям, и минимальна примерно посередине между ними. То есть кривая эффективности зависит от выбора «опорных» точек.

С помощью аппроксимации передаточных характеристик по большему количеству опорных точек, при том же порядке аппроксимирующего полинома, можно увеличить среднюю (от значения входного сигнала) эффективность коррекции.

Проведение аппроксимации с одновременной статистической обработкой данных относится к задачам регрессионного анализа. При этом широко используется оценка среднеквадратической погрешности для всех точек обрабатываемых данных, а сам метод подобного приближения получил названия метода наименьших квадратов (МНК). Данный метод позволяет достаточно точно описать сигнал, даже сильно засоренный шумами, простой математической функцией. При этом критерий минимума среднего квадрата ошибок одновременно является наиболее распространенным критерием оптимальности, применяемым для оценки качества обработки сигнала [4,6].

Коэффициенты коррекции находятся с помощь МНК из системы уравнений:

                                      

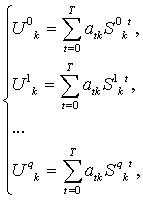
где T – порядок полинома, q – количество точек аппроксимации.

Оценим эффективность линейной коррекции, увеличив число опорных точек до трех.

Основа МНК заключается в следующем. Наиболее вероятными значениями параметров являются те, для которых сумма квадратов отклонений между точками кривой и соответствующими им экспериментальными точками достигает минимума [13].

          

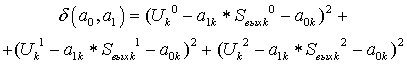
Функция δ в формуле имеет  минимум в точке, в которой выполняются следующие условия:

        

Получаем следующую систему уравнений:

.           

Оценим эффективность линейной коррекции для ПЗС матрицы. Из формул , и при условии равенства эталонной яркости для всех пикселей, а также α=0, c=0, получаем:

,                

где

 

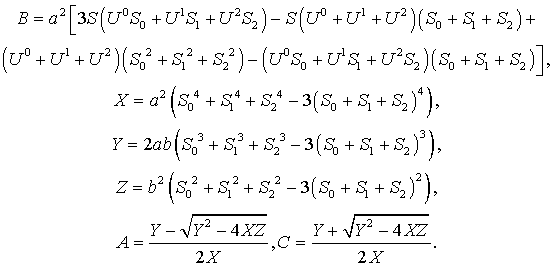
Согласно 

,

Уравнение решается аналогично .

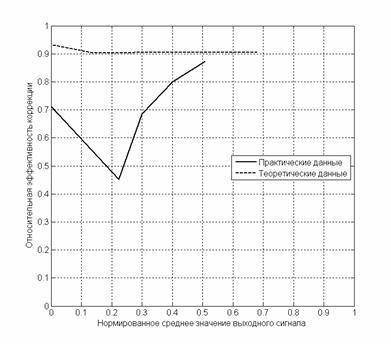
Рис.3 – Графики относительной эффективности коррекции геометрического шума методом линейной коррекции по трем опорным точкам, полученные по практическим и теоретическим данным для ПЗС-матрицы KAI-1003.

 

Аппроксимация характеристики чувствительности практических данных проводилась в программной среде MATLAB с помощью функции «polyfit», использующей МНК [13, 17, 18].

Оптимальное количество точек аппроксимации зависит от характера (линейности) передаточных характеристик конкретной матрицы и подбирается опытным путем.

5       Заключение

Оценим эффективность коррекции геометрического шума с помощью аппроксимации передаточной характеристики каналов полиномом T-го порядка и соотнесем положительный эффект от повышения порядка полинома с необходимыми для коррекции ресурсами.

Для коррекции геометрического шума полиномом T-го порядка требуется T-1 операций сложения и операций умножения на один отсчет.

Необходимый объем памяти V_mem рассчитывается по формуле:

,                                                  

 

где К – количество каналов МФПУ,

V – объем памяти на один коэффициент (32 бит, формат с плавающей запятой).

 

Таблица 1 – Требуемые ресурсы в зависимости от порядка полинома

Порядок	Объем памяти на один канал, бит	Операции сложения	Операции умножения
1	64	1	1
2	96	2	3
3	128	3	6

 

 

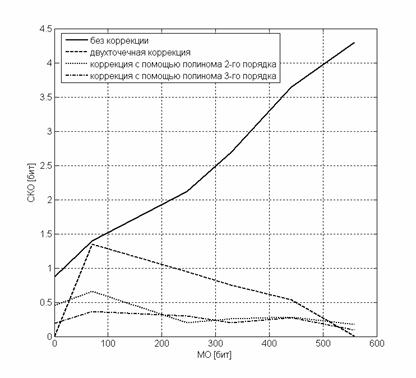
Сравнение результатов коррекции геометрического шума различными методами (без коррекции неравномерности объектива) в зависимости от освещенности изображения, полученных с помощью анализа изображений в системе MATLAB, приведены на рисунке 4. Чтобы не учитывать неравномерность объектива по полю изображения, для оценки геометрического шума используется следующая формула:

 ,                                         

 

где  - среднее значение, рассчитанное по блоку пикселей с текущим пикселем в центре.

Полученные результаты показали, что применение полинома 2-го порядка дает значительный рост эффективности коррекции геометрического шума по сравнению с двухточечной коррекцией. Положительный эффект от повышения полинома  до 3-го порядка в несколько раз меньше и не оправдывает увеличения вычислительных затрат. Дальнейшее увеличение порядка полинома приводит к ошибке аппроксимации сопоставимой с ошибкой квантования.

Т.о. применение  полинома второго порядка в системах автоматической обработки информации в качестве аппроксимирующей  функции обосновано с точки зрения оптимального отношения эффективности коррекции и количества требуемых вычислительных ресурсов.

Рис.4 – Графики среднеквадратического отклонения выходного сигнала от его математического ожидания для ПЗС-матрицы KAI-1003.

Литература

1. Архипов С.А. Коррекция неоднородности чувствительности аппаратуры «Гамма» в условиях эксплуатации./ С.А.Архипов, Н.А.Бутяйкин, В.М.Линько// Системы наблюдения, мониторинга и дистанционного зондирования Земли: Материалы III научно-технической конференции. – М.:  МНТОРЭС им.А.С.Попова, 2006, с.18-21.

2. Болтарь К. О. Тепловизор на основе «смотрящей» матрицы
из Cd0,2Нg0,8Te формата 128х128/ К.О.Болтарь, Л.А.Бовина, Л.Д.Сагинов, В.И.Стафеев, И.С.Гибин, В.М.Малеев// Прикладная физика.- № 2.- 1999.

3. Быков Р.Е. Цифровое преобразование изображений: Учеб. Пособие для вузов/ Р.Е.Быков, Р.Фрайер, К.В.Иванов, А.А.Манцветов; Под ред. Профессора Р.Е.Быкова.-М.: Горячая линия-Телеком.- 2003.- 228 с.

4. Грузман И.С. Цифровая обработка изображений в информационных системах: Учебное пособие/ И.С.Грузман, В.С.Киричук, В.П.Косых, Г.И.Перетягин, А.А.Спектор.-  Новосибисрк: Изд-во НГТУ, 2000. – 168 с.

5.  Двайт Г.Б. Таблицы интегралов и другие формулы: Пер. с англ./ Н.В. Леви. 6-е изд. - М.: Наука.- 1983.- 172 с.

6. Дьяконов В.П. MATLAB 5.3.1 с пакетами расширений./ В.П.Дьяконов, И.В.Абраменкова, В.В.Круглов.- Под ред. Проф. В.П.Дьяконова.-М.: Нолидж.-2001.- 880 с.

7. Лебедев Д.Г. Фильтрация остаточного геометрического и аппаратурного шумов сканирующей матрицы ИК-диапазона с микросканированием.// Д.Г.Лебедев, К.Т.Лыонг Информационные процессы, Том 7, № 3, 2007, с.369-385.

8. Лыонг К.Т. Методы и алгоритмы эффективного управления обработкой видеоинформации в опто-электронных устройствах. Автореферат диссертации на соискание ученой степени кандидата технических наук.- М.- 2007.- 20 с.

9. Малинин В.В. Моделирование и оптимизация оптико-электронных приборов с фотоприемными матрицами. Электронная версия книги. - Новосибирск: ЦИТ СГГА.- 2005. (http://www.ssga.ru/eossib/)

10. Мосягин Г.М. Теория оптико-электронных систем: Учебник для студентов по оптическим специальностям/ Г.М.Мосягин, В.Б.Немтинов, Е.Н.Лебедев.- М.: Машиностроение.- 1990.- 432 с.

11. Пресс Ф.П. Фоточувствительные приборы с зарядовой связью.- М.: Радио и связь.- 1991.- 264 с.

12. Солина Н.И. Выравнивание чувствительности и исправления метрического шума в тепловизионных изображениях методом двухточечной коррекции.// Информационные технологии моделирования и управления: Междунар. сб. науч. тр.– Под ред. д.т.н., проф. О.Я. Кравца. Вып. 15.– Воронеж: Изд-во «Научная книга», 2004.

13. Стаценко В.А. Планирование эксперимента, обработка данных и принятие решений: Курс лекций.- Великий Новгород: НовГУ им.Ярослава Мудрого.- 1999.- 105 с.

14. Стемпковский А. КМОП-фотодиодные СБИС. Перспективная элементная база однокристальных систем приема и обработки информации// Электроника: Нaука, Технология, Бизнес.- 2003.- №2.- с.14-20.

15. Тарасов В.В. Инфракрасные системы «смотрящего» типа./ В.В.Тарасов, Ю.Г.Якушенко.- М.: Логос, 2004.- 444 с.

16. Федоткин М.А. Основы прикладной теории вероятности и статистики.- М.: Высшая школа.- 2006.- 368 с.

17. Форсайт Д. Компьютерное зрение. Современный подход.: Пер. с англ./ Д.Форсайт, Ж.Понс.- М.: Издательский дом «Вильямс».- 2004.- 928 с.

18. Яне Б. Цифровая обработка изображений.- М.: Техносфера.- 2007.- 584с.

19. Borovytsky V.N. Residual error after non-uniformity correction// Semiconductor Physics, Quantum Electronics & Optoelectronics.- 2000.- V. 3, N 1.– P. 102-105.

20. Burns R.D. Improved techniques for object location  with CMOS image sensors. Master’s thesis.- University of Waterloo.- 2003.-P.77.

21. CCD Image Sensor Noise Sources. Application note. Revision 2.1.- Kodak.- 2005.- P.7. (http://www.kodak.com/go/imagers)

22. Kiyoya Y. Most suitable non-uniformity correction method for PiSi SBD detector// SPIE Proc.- 1998.- V.3377.- P.114-121.

23. Lim S.H. Video processing applications of high speed CMOS image sensors. Ph.D. dissertation.- Stanford University.- 2003.- P.90.