Электронный транспорт через контакт квантовой проволоки с объемными электродами
П. П. Асеев 1, 2, С. Н. Артёменко 1, 2
1 Институт радиотехники и электроники им. В.А.Котельникова РАН, Москва
2 Московский физико-технический институт
Получена 3 ноября 2011 г.
Аннотация. Теоретически исследовано влияние
межэлектронного взаимодействия на электронный транспорт через контакты
одномерного (1D) проводника с металлическими 2D- или 3D-электродами.
Рассмотрен случай поляризованных по спину электронов, описываемых на основе
гамильтониана Томонаги-Латтинджера. Выведены граничные условия, связывающие ток
и плотность заряда на границе 1D проводника с приложенным к электродам
электрическим потенциалом (постоянным или переменным), получены также граничные
условия для флуктуаций. Показано, что если контакт не является
адиабатическим, то фриделевские осцилляции плотности заряда, возникающие вблизи
контакта в 1D-системе, сильно подавляют проводимость системы аналогично
действию примесей в системах 1D электронов с отталкиванием.
Если приложенное постоянное напряжение превышает пороговое значение ![]()
![]() проводимость резко
увеличивается, причем протекание постоянного тока
проводимость резко
увеличивается, причем протекание постоянного тока ![]() сопровождается генерацией колебаний тока
с частотой
сопровождается генерацией колебаний тока
с частотой ![]() .
.
Ключевые слова: квантовая проволока, граничные условия, взаимодействие между электронами, электронный транспорт.
Abstract. We study theoretically how
interelectron interaction affects an electron transport through contacts of
one-dimensional (1D) conductor with metallic 2D or 3D leads. We consider
spin-polarized electron described by Tomonaga-Luttinger Hamiltonian. We derive
boundary conditions which connect current and charge density at the boundary of
1D conductor with applied ac or dc electric potential. We also derive boundary
conditions for fluctuations. It is shown, that if the contact is not adiabatic
one, then Friedel oscillations of charge density in 1D conductor near the
contact strongly suppress conductivity. The effect is similar to effect of
impurities in 1D electron systems with repulsion. If the applied voltage is
higher than ![]() the conductance increases drastically, with dc current
the conductance increases drastically, with dc current ![]() being
accompanied by coherent oscillations of frequency
being
accompanied by coherent oscillations of frequency![]() .
.
Key words: quantum wire, boundary conditions, electron-electron interaction, electron transport.
Введение
В последнее время в связи со стремительным развитием технологий микро- и наноэлектроники возник повышенный интерес к наноразмерным системам. Миниатюризация приборов электроники не сводится только к изменению геометрических характеристик, потому что когда размеры системы сравниваются с длиной волны электронов, происходит качественное изменение физических свойств. В структурах, которые доступны уже сегодняшней технологии, наблюдают квантовомеханические явления, в значительно мере влияющие на электрофизические свойства приборов. При этом такие явления специфические именно для систем с линейными размерами нанометрового диапазона. Теоретические методы, основанные на решении квазиклассических уравнений, в частности, кинетического уравнения Больцмана, использовавшиеся для описания традиционных электронных приборов, уже не способны описывать подобные явления, которые существенным образом меняют характер электронного транспорта.
Как известно, в отличие от 2D и 3D электронных систем, где основные электронные свойства, как правило, описывают в рамках ферми-жидкости Ландау, основанной на представлении об одноэлектронных квазичастицах, которые ведут себя подобно невзаимодействующим электронам, взаимодействие в 1D системах приводит к качественным изменениям в электронной структуре и транспорте, в частности, к степенному понижению плотности состояний вблизи энергии Ферми и сильному подавлению проводимости даже единственной примесью [1], которое выражается в степенной зависимости проводимости от напряжения и/или температуры. Такое поведение соответствует жидкости Латтинджера, являющейся альтернативой ферми-жидкости в 1D системах (см. обзор [2]). Экспериментальные подтверждения подавления проводимости были получены на многих 1D системах, в частности, в полупроводниковых квантовых проводах [3] и углеродных нанотрубках [4].
Степенные вольт-амперные характеристики (ВАХ) описывают в
терминах макроскопического туннелирования между минимумами периодического
потенциала, связанного с фриделевскими осцилляциями, формирующимися вокруг
примеси. В недавней теоретической работе [5] было показано, что режим степенных
ВАХ можно наблюдать только в области достаточно малых напряжений, а при
напряжениях выше порогового, связанного с перенормированной 1D флуктуациями
величиной потенциала примеси, был предсказан динамический режим, при котором
протекание постоянного тока сопровождается генерацией колебаний с частотой ![]() , где
, где ![]() – постоянная компонента
тока,
– постоянная компонента
тока, ![]() – заряд
электрона. Этот эффект возникает благодаря межэлектронному отталкиванию, он не
может быть описан в рамках подходов, основанных на невзаимодействующих
электронах. Эффект связан с движением фриделевских осцилляций при протекании
постоянного тока. Формирование фриделевских осцилляций и возникновение похожих
эффектов следует ожидать и на резких, не адиабатических, контактах 1D системы
взаимодействующих электронов с 2D или 3D электродами.
– заряд
электрона. Этот эффект возникает благодаря межэлектронному отталкиванию, он не
может быть описан в рамках подходов, основанных на невзаимодействующих
электронах. Эффект связан с движением фриделевских осцилляций при протекании
постоянного тока. Формирование фриделевских осцилляций и возникновение похожих
эффектов следует ожидать и на резких, не адиабатических, контактах 1D системы
взаимодействующих электронов с 2D или 3D электродами.
Задача о протекании тока через контакт между 1D системой электронов в коррелированном состоянии жидкости Латтинджера и электродами более высокой размерности с электронами, образующими ферми-жидкость, все еще не изучена. Обычно в таких случаях используют граничные условия, выведенные [6, 7] для идеальных адиабатических контактов. Эти условия выведены только для средних величин и поэтому их недостаточно для описания флуктуаций, которые, как хорошо известно, очень велики в 1D-системах. Кроме того, реальные контакты не обязательно являются адиабатическими, поэтому следует ожидать что электроны будут испытывать от них отражения, что должно привести к формированию фриделевских осцилляций, сильно влияющих на электронный транспорт в 1D системе. В этой работе мы выводим граничные условия для не адиабатических контактов и показываем, что в этом случае действительно у контакта возникают фриделевские осцилляции, которые подавляют омическую проводимость, что как и в случае примеси [5] приводит к динамическому режиму проводимости, напоминающему эффект Джозефсона и кулоновскую блокаду.
Далее примем равными единице заряд электрона ![]() , постоянную Планка
, постоянную Планка ![]() и постоянную Больцмана
и постоянную Больцмана ![]() , возвращаясь к
размерным единицам, где это необходимо, в конечных формулах.
, возвращаясь к
размерным единицам, где это необходимо, в конечных формулах.
1. Вывод граничных условий
Для вывода граничных условий воспользуемся идеями теории
рассеяния (см., например, обзор [8]). 1D проводник длиной ![]() представляет из себя
потенциальный барьер при
представляет из себя
потенциальный барьер при ![]() , содержащий в себе проводящий канал вдоль
оси
, содержащий в себе проводящий канал вдоль
оси ![]() .
Проводник соединяется с двумя симметричными подводящими объјмными электродами.
Мы проведем рассуждения для 3D электродов; вывод для случая 2D электродов
повторяет эти рассуждения дословно. Потенциал системы 1D проводник–электроды
можно записать в виде:
.
Проводник соединяется с двумя симметричными подводящими объјмными электродами.
Мы проведем рассуждения для 3D электродов; вывод для случая 2D электродов
повторяет эти рассуждения дословно. Потенциал системы 1D проводник–электроды
можно записать в виде:
![]() ,
(1)
,
(1)
где
координаты ![]() и
и ![]() обозначены единым
символом
обозначены единым
символом ![]() ,
, ![]() –
– ![]() -функция Хевисайда, а
-функция Хевисайда, а ![]() – профиль потенциала 1D-проводника.
Предполагается, что уровень Ферми
– профиль потенциала 1D-проводника.
Предполагается, что уровень Ферми ![]() находится между первым и вторым уровнем
размерного квантования 1D проводника. Поскольку рассуждения для левого и
правого контакта одинаковы, рассмотрим подробно только левый контакт, а
результат для правого контакта приведем без вывода.
находится между первым и вторым уровнем
размерного квантования 1D проводника. Поскольку рассуждения для левого и
правого контакта одинаковы, рассмотрим подробно только левый контакт, а
результат для правого контакта приведем без вывода.
Рассмотрим
для начала случай, когда электроны не взаимодействуют ни в электродах, ни в 1D
проводнике. В области проводящего 1D канала полевой оператор ![]() можно разложить по
собственным функциям
можно разложить по
собственным функциям ![]() самосопряженного
оператора
самосопряженного
оператора ![]() ,
где
,
где ![]() –
эффективная масса электрона:
–
эффективная масса электрона:
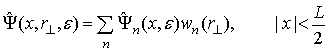 ,
(2)
,
(2)
При
энергиях ![]() порядка
порядка
![]() полевые
операторы
полевые
операторы ![]() , соответствующие
верхним модам
, соответствующие
верхним модам ![]() экспоненциально
убывают вглубь проводника
экспоненциально
убывают вглубь проводника
где
![]() , а
, а ![]() – энергия,
соответствующая
– энергия,
соответствующая ![]() -ой
моде размерного квантования. Таким образом, вклад в проводимость дает только
оператор
-ой
моде размерного квантования. Таким образом, вклад в проводимость дает только
оператор ![]() ,
соответствующий нижней подзоне размерного квантования. Пусть
,
соответствующий нижней подзоне размерного квантования. Пусть ![]() – поперечные волновые
функции в электродах с соответствующими собственными энергиями
– поперечные волновые
функции в электродах с соответствующими собственными энергиями ![]() . Тогда полевой оператор
в электродах можно представить в виде суммы волн, движущихся слева направо и
справа налево, а также волн, экспоненциально затухающих вглубь электрода:
. Тогда полевой оператор
в электродах можно представить в виде суммы волн, движущихся слева направо и
справа налево, а также волн, экспоненциально затухающих вглубь электрода:
![]() ,
(4)
,
(4)
причем волна, распространяющаяся вправо, имеет вид
 (5)
(5)
волна, распространяющаяся влево, имеет вид
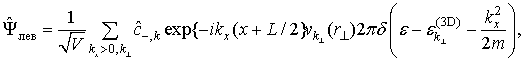 (6)
(6)
и волна, затухающая вглубь электрода, имеет вид
 (7)
(7)
где
![]() – объем
электрода. Операторы
– объем
электрода. Операторы ![]() ,
соответствующие волнам, распространяющимся слева направо, совпадают с
равновесными операторами уничтожения электронов. Далее обозначим
,
соответствующие волнам, распространяющимся слева направо, совпадают с
равновесными операторами уничтожения электронов. Далее обозначим ![]() .
.
Чтобы теперь получить граничное условие, связывающее полевой
оператор в проволоке ![]() ,
соответствующий нижней подзоне размерного квантования, и операторы уничтожения
электронов
,
соответствующий нижней подзоне размерного квантования, и операторы уничтожения
электронов ![]() ,
нужно воспользоваться непрерывностью полевого оператора и его производной при
,
нужно воспользоваться непрерывностью полевого оператора и его производной при ![]() . Учитывая , получаем систему уравнений:
. Учитывая , получаем систему уравнений:
![]() (9)
(9)
где
![]() , причем в
случае отрицательного подкоренного выражения выбирается такая ветвь функции
, причем в
случае отрицательного подкоренного выражения выбирается такая ветвь функции ![]() , что
, что ![]() . Выразив из
. Выразив из ![]() и, пользуясь тем, что
и, пользуясь тем, что
![]()
где ![]() , получим
, получим
В
случае общего положения, матрица ![]() невырождена. Пусть
невырождена. Пусть ![]() – матрица, обратная к ней.
Тогда, действуя слева на левую и правую часть равенства матрицей
– матрица, обратная к ней.
Тогда, действуя слева на левую и правую часть равенства матрицей ![]() и, проецируя, на
и, проецируя, на
![]() , получим
граничное условие
, получим
граничное условие
где
![]()
![]()
![]()
– коэффициенты, которые определяются формой потенциала. В граничном условии для правого контакта эти коэффициенты заменяем на комплексно-сопряженные
Задачу
нахождения коэффициентов ![]() ,
, ![]() ,
, ![]() для заданного профиля потенциала
для заданного профиля потенциала ![]() можно решать лишь численно, но удается записать
аналитические соотношения между этими коэффициентами, пользуясь соотношениями
антикоммутации
можно решать лишь численно, но удается записать
аналитические соотношения между этими коэффициентами, пользуясь соотношениями
антикоммутации ![]() .
Найдя полевой оператор в 1D проводнике с граничными условиями (11)–(12), можно
получить, что фермионные антикоммутационные соотношения выполняются тогда и
только тогда, если
.
Найдя полевой оператор в 1D проводнике с граничными условиями (11)–(12), можно
получить, что фермионные антикоммутационные соотношения выполняются тогда и
только тогда, если
где
для дальнейшего удобства обозначено ![]() . Также окажется полезно, вычислив
проводимость, связать коэффициенты
. Также окажется полезно, вычислив
проводимость, связать коэффициенты![]() ,
, ![]() и
и ![]() с прозрачностью
с прозрачностью ![]() системы
системы
где
![]() –
импульс
Ферми в 1D проводнике. Теперь умножим граничные условие – слева на
сопряженные, вычтем из полученных равенств термодинамическое среднее
при нулевом
напряжении. Тогда, пользуясь соотношениями – перейдем к временному
представлению и получим граничные условия для операторов плавно
меняющегося возмущения
плотности заряда
–
импульс
Ферми в 1D проводнике. Теперь умножим граничные условие – слева на
сопряженные, вычтем из полученных равенств термодинамическое среднее
при нулевом
напряжении. Тогда, пользуясь соотношениями – перейдем к временному
представлению и получим граничные условия для операторов плавно
меняющегося возмущения
плотности заряда ![]() ,
тока
,
тока ![]() и
и ![]() -компоненты плотности
заряда (фриделевской осцилляции)
-компоненты плотности
заряда (фриделевской осцилляции) ![]() на левом(правом) контакте
на левом(правом) контакте
где
![]() .
.
Мы
проверили, выполняется ли граничное условие в случае простой геометрии
контакта, позволяющей решить задачу аналитически и найти явный вид
коэффициентов ![]() ,
, ![]() ,
, ![]() . В качестве
такой модели мы рассмотрели контакт, в котором металлический электрод
расширяется достаточно плавно, так что контакт близок к адиабатическому, и к
тому же может содержать ступеньку в зависимости потенциальной энергии от
. В качестве
такой модели мы рассмотрели контакт, в котором металлический электрод
расширяется достаточно плавно, так что контакт близок к адиабатическому, и к
тому же может содержать ступеньку в зависимости потенциальной энергии от ![]() , то есть предполагается,
что дно энергетической зоны внутри проводящего канала выше на величину
, то есть предполагается,
что дно энергетической зоны внутри проводящего канала выше на величину ![]() . В этом случае мы можем
воспользоваться квазиклассическим приближением в области электрода и сшить
полученное таким образом решение вне 1D канала с точным решением внутри канала
для случая невзаимодействующих электронов. Оказалось, что для такой системы
граничное условие дает правильное выражение для омической проводимости
контакта,
. В этом случае мы можем
воспользоваться квазиклассическим приближением в области электрода и сшить
полученное таким образом решение вне 1D канала с точным решением внутри канала
для случая невзаимодействующих электронов. Оказалось, что для такой системы
граничное условие дает правильное выражение для омической проводимости
контакта, ![]() ,
согласующееся с формулой Ландауэра (здесь
,
согласующееся с формулой Ландауэра (здесь ![]() – квант проводимости).
– квант проводимости).
Таким
образом, граничные условия позволяют решить задачу о проводимости в случае
невзаимодействующих электронов, когда фриделевская осцилляция не приводит к
подавлению проводимости. Теперь нужно решить задачу с учетом межэлектронного
взаимодействия в квантовом проводе, для чего мы воспользуемся бозонизованным
гамильтонианом Томонаги-Латтинджера для поляризованной по спину электронной
жидкости. Электронная система описывается с помощью бозонного поля смещения ![]() . Возмущения плотности
заряда и ток выражаются через
. Возмущения плотности
заряда и ток выражаются через ![]() с помощью соотношений
с помощью соотношений
 (16)
(16)
В
этом подходе межэлектронное взаимодействие считается короткодействующим: такая
ситуация встречается в квантовых проводах с металлическим затвором,
экранирующим дальнодействующую часть кулоновского взаимодействия [7]. Величина
взаимодействия характеризуется параметром ![]() , таким что
, таким что ![]() в случае межэлектронного отталкивания, а
в случае межэлектронного отталкивания, а ![]() соответствует
невзаимодействующим электронам. Для квантовых проводов можно воспользоваться
грубой оценкой
соответствует
невзаимодействующим электронам. Для квантовых проводов можно воспользоваться
грубой оценкой ![]() ,
,
![]() –
диэлектрическая проницаемость окружающей среды.
–
диэлектрическая проницаемость окружающей среды.
В гайзенберговском представлении ![]() удовлетворяет волновому
уравнению [2]
удовлетворяет волновому
уравнению [2]
где
![]() – скорость
плазменных волн. Это уравнение мы должны решить с граничными условиями для
– скорость
плазменных волн. Это уравнение мы должны решить с граничными условиями для ![]() на
контакте, которые
можно получить с помощью бозонизации условия . При этом надо учесть еще
одно обстоятельство. В теории жидкости Латтинджера предполагается
линейный закон
дисперсии электронов, поэтому она применима к реальным системам только
тогда,
когда все характерные энергии системы мало отличаются от энергии Ферми.
Однако,
если переписать слагаемое, представляющее фриделевскую осцилляцию в , в
бозонизованной форме, оно приобретает вид
на
контакте, которые
можно получить с помощью бозонизации условия . При этом надо учесть еще
одно обстоятельство. В теории жидкости Латтинджера предполагается
линейный закон
дисперсии электронов, поэтому она применима к реальным системам только
тогда,
когда все характерные энергии системы мало отличаются от энергии Ферми.
Однако,
если переписать слагаемое, представляющее фриделевскую осцилляцию в , в
бозонизованной форме, оно приобретает вид ![]() . В общем случае эта величина порядка
энергии Ферми и становится малой лишь при
. В общем случае эта величина порядка
энергии Ферми и становится малой лишь при ![]() , когда контакт близок к адиабатическому.
Поэтому мы обратимся именно к случаю
, когда контакт близок к адиабатическому.
Поэтому мы обратимся именно к случаю ![]() . Кроме того, мы должны учесть
экранирование потенциала электрода затвором, как это сделано в [6,
7]. В
результате мы получим следующие граничные условия для бозонного поля
. Кроме того, мы должны учесть
экранирование потенциала электрода затвором, как это сделано в [6,
7]. В
результате мы получим следующие граничные условия для бозонного поля ![]() на контактах при
на контактах при ![]() :
:
где
![]() и
и ![]() – правая часть
граничных условий для левого и правого контактов соответственно.
– правая часть
граничных условий для левого и правого контактов соответственно.
Для
вычисления корреляционных функций потребуется вычислить корреляторы от
флуктуирующих частей ![]() .
В частотном представлении можно записать
.
В частотном представлении можно записать
.
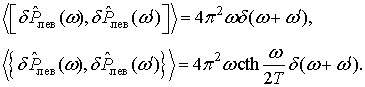 (19)
(19)
Выделим
теперь среднюю и флуктуирующие части полевого оператора, ![]() и проведем термодинамическое
усреднение уравнений. Получим граничные условия для средних значений
и проведем термодинамическое
усреднение уравнений. Получим граничные условия для средних значений
где
![]() ,
, ![]() – электрический
потенциал, приложенный к каждому из электродов. Видно, что уравнение для
средних значений
– электрический
потенциал, приложенный к каждому из электродов. Видно, что уравнение для
средних значений ![]() ,
которые определяют средний ток и возмущения плотности заряда в проводе вблизи
контакта содержит также вклад от фриделевских осцилляций, который определяется
флуктуациями в 1D-канале. В случае адиабатического контакта
,
которые определяют средний ток и возмущения плотности заряда в проводе вблизи
контакта содержит также вклад от фриделевских осцилляций, который определяется
флуктуациями в 1D-канале. В случае адиабатического контакта ![]() , фриделевские осцилляции
выпадают и сводится к граничным условиям Эггера и Граберта [6,
7].
, фриделевские осцилляции
выпадают и сводится к граничным условиям Эггера и Граберта [6,
7].
2. Модификация граничных условий при переменном приложенном напряжении
В случае, когда к массивному электроду приложено переменное напряжение, правая часть может модифицироваться.
где в случае постоянного напряжение ![]() зависит только от
разностного времени и имеет вид
зависит только от
разностного времени и имеет вид
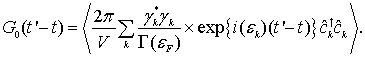 (22)
(22)
Если
приложен переменный электрический потенциал ![]() , то фаза гейзенберговских волновых
операторов сдвигается на интеграл по времени от сдвига потенциала:
, то фаза гейзенберговских волновых
операторов сдвигается на интеграл по времени от сдвига потенциала:
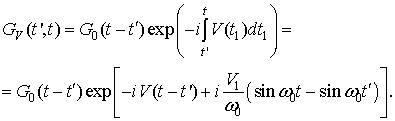 (23)
(23)
Теперь функция Грина ![]() зависит не только от
разностного времени, но и от суммарного. Переходя к энергетическому
представлению по разностному времени и к временному по суммарному, получаем:
зависит не только от
разностного времени, но и от суммарного. Переходя к энергетическому
представлению по разностному времени и к временному по суммарному, получаем:
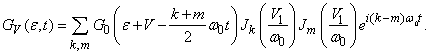 (24)
(24)
Отсюда следует, что в случае,
когда к массивному электроду приложено переменное напряжение, может возникнуть
необходимость модифицировать граничные условия , и в них проявятся квантовые свойства при ![]() .
.
Правую часть граничных условий считаем, пользуясь . Тогда получаем
В равновесном случае функция
Грина ![]() сводится
к произведению плотности состояний на
сводится
к произведению плотности состояний на ![]() . Интеграл по энергии в легко вычислить в случае, когда функция Грина массивного электрода сводится к равновесной
функции распределения, а зависимостью плотности состояний от энергии мы
пренебрегаем. В этом случае
. Интеграл по энергии в легко вычислить в случае, когда функция Грина массивного электрода сводится к равновесной
функции распределения, а зависимостью плотности состояний от энергии мы
пренебрегаем. В этом случае ![]() , и для оператора в правой части граничных
условий получается
, и для оператора в правой части граничных
условий получается
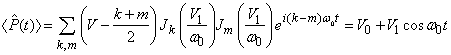 (26)
(26)
3. Пороговое напряжение
Если контакт идеальный, т.е. ![]() , то решая волновое уравнение совместно с граничными условиями , можно найти омический ток
, то решая волновое уравнение совместно с граничными условиями , можно найти омический ток ![]() В общем случае, когда
В общем случае, когда ![]() , задача нахождения тока,
протекающего через систему, усложняется засчет нелинейных слагаемых в граничных
условиях , соответствующих фриделевским осцилляциям, причем основную сложность составляет
учет флуктуаций. Предположим, что флуктуации гауссовы. Строго говоря,
флуктуации не являются гауссовыми, но модель гауссовых флуктуаций является
хорошим приближением в случае сильного межэлектронного отталкивания
, задача нахождения тока,
протекающего через систему, усложняется засчет нелинейных слагаемых в граничных
условиях , соответствующих фриделевским осцилляциям, причем основную сложность составляет
учет флуктуаций. Предположим, что флуктуации гауссовы. Строго говоря,
флуктуации не являются гауссовыми, но модель гауссовых флуктуаций является
хорошим приближением в случае сильного межэлектронного отталкивания ![]() и в пределе больших
напряжений. Ситуация здесь напоминает задачу о протекании тока через примесь в
квантовом проводе, где в аналогичных случаях флуктуации также оказываются
близки к гауссовым [9].
и в пределе больших
напряжений. Ситуация здесь напоминает задачу о протекании тока через примесь в
квантовом проводе, где в аналогичных случаях флуктуации также оказываются
близки к гауссовым [9].
Рассмотрим несколько предельных случаев, допускающих
аналитическое решение. Обратимся сначала к случаю, когда к электродам приложен
потенциал ![]() ,
и
будем искать стационарное решение. В этом случае из уравнения движения
следует, что средняя фаза линейно зависит от координаты:
,
и
будем искать стационарное решение. В этом случае из уравнения движения
следует, что средняя фаза линейно зависит от координаты: ![]() . Тогда из граничных условий следует
. Тогда из граничных условий следует
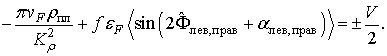 (27)
(27)
Значит,
если среднее от осциллирующих слагаемых, не обращается в нуль, то существует
пороговое напряжение ![]() ,
при котором еще существует решение с нулевым током
,
при котором еще существует решение с нулевым током
Последнее равенство выполняется в гармоническом самосогласованном приближении. Граничные условия для флуктуирующей фазы
в этом приближении выглядят следующим образом:
где
![]() вычисляется
самосогласованно. Теперь можно решать уравнение движения совместно с
граничными условиями и вычислить корреляционную функцию для фазы на
контакте.
Из условия симметрии
вычисляется
самосогласованно. Теперь можно решать уравнение движения совместно с
граничными условиями и вычислить корреляционную функцию для фазы на
контакте.
Из условия симметрии ![]() можно
получить
можно
получить ![]() , а корреляционная
функция для фазы на контактах в частотном представлении для высоких частот
, а корреляционная
функция для фазы на контактах в частотном представлении для высоких частот ![]() имеет вид
имеет вид
Помимо логарифмически расходящейся части это выражение
содержит осциллирующий множитель, связанный с многократными отражениями
флуктуаций от контактов. Если длина квантового провода достаточно велика, ![]() , эти осцилляции дают
лишь малый вклад в интеграл, поэтому осциллирующий множитель можно заменить его
средним по периоду осцилляций значением. Далее результат интегрирования зависит
от соотношения между температурой
, эти осцилляции дают
лишь малый вклад в интеграл, поэтому осциллирующий множитель можно заменить его
средним по периоду осцилляций значением. Далее результат интегрирования зависит
от соотношения между температурой ![]() и
и ![]() . Для длинного провода,
. Для длинного провода, ![]() , при нулевой температуре с
логарифмической точностью получаем
, при нулевой температуре с
логарифмической точностью получаем
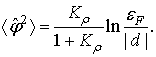 (31)
(31)
Так
как ![]() зависит
от
зависит
от ![]() , то это
уравнение является уравнением самосогласования для
, то это
уравнение является уравнением самосогласования для ![]() . Самосогласованное решение для
среднего квадрата флуктуаций имеет вид
. Самосогласованное решение для
среднего квадрата флуктуаций имеет вид
 (32)
(32)
Теперь с помощью мы можем найти пороговое напряжение
![]() (33)
(33)
Видно,
что при межэлектронном отталкивании, когда ![]() , средний квадрат флуктуаций
, средний квадрат флуктуаций ![]() и амплитуда
фриделевских осцилляций
и амплитуда
фриделевских осцилляций ![]() конечны, а в отсутствие межэлектронного
взаимодействия, при
конечны, а в отсутствие межэлектронного
взаимодействия, при ![]() ,
флуктуации становятся бесконечными и разрушают фриделевские осцилляции,
,
флуктуации становятся бесконечными и разрушают фриделевские осцилляции, ![]() . Отметим, что роль
фриделевских осцилляций здесь аналогична их роли в случае примесей. Таким
образом мы получили, что при приложении к контактам напряжения
. Отметим, что роль
фриделевских осцилляций здесь аналогична их роли в случае примесей. Таким
образом мы получили, что при приложении к контактам напряжения ![]() ток через контакт не
течет. Этот результат связан с тем, что мы учли только гауссовы флуктуации.
Если бы мы учли флуктуации солитонного типа, при которых в результате
туннелирования фаза возрастает на
ток через контакт не
течет. Этот результат связан с тем, что мы учли только гауссовы флуктуации.
Если бы мы учли флуктуации солитонного типа, при которых в результате
туннелирования фаза возрастает на ![]() , мы получили бы маленький туннельный ток и
при
, мы получили бы маленький туннельный ток и
при ![]() .
Флуктуации такого типа изучали применительно к примесям, где они приводили к
степенным ВАХ [1]. Отметим, что в рассмотренном нами случае контактов, близких
к адиабатическим, мы получили
.
Флуктуации такого типа изучали применительно к примесям, где они приводили к
степенным ВАХ [1]. Отметим, что в рассмотренном нами случае контактов, близких
к адиабатическим, мы получили ![]() , что означает, что подход, основанный на
модели Томонаги-Латтинджера, применим. С уменьшением прозрачности канала
величина порогового поля увеличивается, приближаясь к энергии Ферми, и наш
подход перестает работать.
, что означает, что подход, основанный на
модели Томонаги-Латтинджера, применим. С уменьшением прозрачности канала
величина порогового поля увеличивается, приближаясь к энергии Ферми, и наш
подход перестает работать.
Рассмотрим теперь случай высоких температур. Интегрирование при температурах ![]() приводит
к уравнению самосогласования, которое не дает конечного порогового напряжения
приводит
к уравнению самосогласования, которое не дает конечного порогового напряжения ![]() . Более тщательное
решение показывает, что имеется пороговая температура
. Более тщательное
решение показывает, что имеется пороговая температура ![]() , выше которой фриделевская
осцилляция разрушается тепловыми флуктуациями и не влияет на проводимость
канала.
, выше которой фриделевская
осцилляция разрушается тепловыми флуктуациями и не влияет на проводимость
канала.
Обратимся
теперь к случаю достаточно короткого канала, ![]() . В этом случае уже нельзя производить
усреднение выражения по осцилляциям при
. В этом случае уже нельзя производить
усреднение выражения по осцилляциям при ![]() , при таких частотах зависимость
, при таких частотах зависимость ![]() в по-прежнему пропорциональна
в по-прежнему пропорциональна ![]() ,
но с другим коэффициентом пропорциональности, что приводит к тому, что
амплитуда фриделевских осцилляций подавляется квантовыми флуктуациями. В
результате оказывается,
,
но с другим коэффициентом пропорциональности, что приводит к тому, что
амплитуда фриделевских осцилляций подавляется квантовыми флуктуациями. В
результате оказывается,
что
при ![]() фриделевские
осцилляции не влияют на проводимость.
фриделевские
осцилляции не влияют на проводимость.
4. Нестационарный режим проводимости
При
увеличении напряжения выше критического значения ![]() происходит переход к нестационарному
режиму проводимости, при котором средняя величина растет во времени и
осциллирует. Этот режим во многом аналогичен рассмотренному в [5,
9]
динамическому режиму протекания тока через примесь. Мы рассмотрим этот режим в
пределе низких температур
происходит переход к нестационарному
режиму проводимости, при котором средняя величина растет во времени и
осциллирует. Этот режим во многом аналогичен рассмотренному в [5,
9]
динамическому режиму протекания тока через примесь. Мы рассмотрим этот режим в
пределе низких температур ![]() и длинных контактов
и длинных контактов ![]() . При напряжениях, незначительно
превышающих пороговое поле, рост фазы происходит в виде ступенек, что
соответствует импульсам тока. Детальный анализ ВАХ в этой области напряжений
затруднен, причем основной трудностью является корректный учет флуктуаций,
средний квадрат которых тоже периодическим образом зависит от времени. Решение
нестационарной задачи облегчается в области высоких напряжений
. При напряжениях, незначительно
превышающих пороговое поле, рост фазы происходит в виде ступенек, что
соответствует импульсам тока. Детальный анализ ВАХ в этой области напряжений
затруднен, причем основной трудностью является корректный учет флуктуаций,
средний квадрат которых тоже периодическим образом зависит от времени. Решение
нестационарной задачи облегчается в области высоких напряжений ![]() ,
когда средний квадрат
флуктуаций фазы почти не зависит от времени, а его осциллирующая часть
мала. В
этом случае уравнение совместно с граничными условиями можно решать по
теории возмущений, считая осциллирующую по времени часть малой как в
флуктуациях
,
когда средний квадрат
флуктуаций фазы почти не зависит от времени, а его осциллирующая часть
мала. В
этом случае уравнение совместно с граничными условиями можно решать по
теории возмущений, считая осциллирующую по времени часть малой как в
флуктуациях ![]() ,
так и в средней фазе
,
так и в средней фазе ![]() .
.
Удобно
переписать волновое уравнение и граничные условие в виде одного уравнения на фазу ![]() .
Воспользуемся формулой д’Аламбера для общего решения волнового уравнения
.
Воспользуемся формулой д’Аламбера для общего решения волнового уравнения
Выражая
![]() из граничного
условия на левом контакте и подставляя в граничное условие на правом
контакте, получим уравнение в частотном представлении
из граничного
условия на левом контакте и подставляя в граничное условие на правом
контакте, получим уравнение в частотном представлении
где
![]() – операторы,
соответствующие фриделевским осцилляциям у каждого из контактов,
– операторы,
соответствующие фриделевским осцилляциям у каждого из контактов,

В
режиме заданного тока средняя фаза растет линейно по времени![]() . Выделим в поле
. Выделим в поле ![]() термодинамическое
среднее и флуктуирующую компоненты
термодинамическое
среднее и флуктуирующую компоненты ![]() . Уравнение для флуктуаций фазы имеет вид
. Уравнение для флуктуаций фазы имеет вид
где
в самосогласованном гармоническом приближении ![]() . Мы предположили, что, как и в
стационарном режиме,
. Мы предположили, что, как и в
стационарном режиме, ![]() .
.
Отметим, что квадрат флуктуаций теперь зависит от времени,
причем эта зависимость периодичная с частотой ![]() . Если
. Если ![]() , то основной вклад в квадрат флуктуаций
дает постоянное во времени слагаемое, а осциллирующая часть мала по сравнению с
ней и убывает с ростом частоты
, то основной вклад в квадрат флуктуаций
дает постоянное во времени слагаемое, а осциллирующая часть мала по сравнению с
ней и убывает с ростом частоты ![]() . Таким образом в
. Таким образом в ![]() можно выделить постоянное во
времени и осциллирующие слагаемые
можно выделить постоянное во
времени и осциллирующие слагаемые
причем
![]() . Мы
предположили, что старшие гармоники дают незначительный вклад в квадрат
флуктуаций. В дальнейшем мы не учитываем слагаемые, оставляя только нулевую и
первые гармоники. Для
. Мы
предположили, что старшие гармоники дают незначительный вклад в квадрат
флуктуаций. В дальнейшем мы не учитываем слагаемые, оставляя только нулевую и
первые гармоники. Для ![]() можно
получить выражение в частотном представлении
можно
получить выражение в частотном представлении
![]() (38)
(38)
Выразив
![]() через
через ![]() с помощью , перепишем уравнение
с помощью , перепишем уравнение
где введены следующие обозначения:
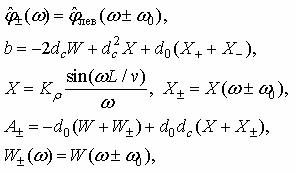
![]()
![]()
Уравнение
линейно, поэтому его решение можно выразить через операторы ![]() :
:
где
![]() – функция Грина
уравнения . Тогда, подставляя в уравнение , получим уравнение на функцию Грина
– функция Грина
уравнения . Тогда, подставляя в уравнение , получим уравнение на функцию Грина ![]() :
:
Решение уравнения можно искать в виде
![]()
Поскольку
мы интересуемся только нулевой и первыми гармониками, считая, что оставшиеся
гармоники дают пренебрежимо малый вклад, то в сумме по ![]() оставляем только
оставляем только ![]() .
Приравнивая коэффициенты перед
.
Приравнивая коэффициенты перед ![]() в левой и правой части , мы сводим исходное уравнение к системе уравнений на
в левой и правой части , мы сводим исходное уравнение к системе уравнений на ![]() :
:
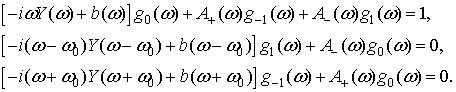 (42)
(42)
Решив систему линейных уравнений, получаем
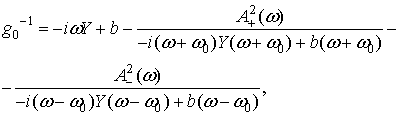 (43)
(43)
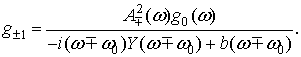 (44)
(44)
Для
частот, не лежащих в узкой полосе шириной ![]() вокруг
вокруг ![]() , можно
воспользоваться приблизительным выражением
, можно
воспользоваться приблизительным выражением
![]() (45)
(45)
Зная
функции Грина ![]() ,
,
![]() , можно,
пользуясь , найти
, можно,
пользуясь , найти ![]() ,
а значит и вычислить средний квадрат флуктуаций. Вклад в
,
а значит и вычислить средний квадрат флуктуаций. Вклад в ![]() , изменяющийся как
, изменяющийся как ![]() равен
равен
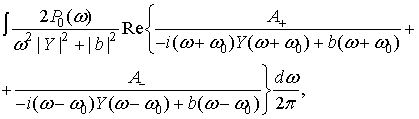
где
![]() находят из
выражения
находят из
выражения
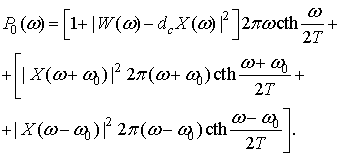 (46)
(46)
Расчет
для низких температур ![]() и
для большой длины 1D проводника
и
для большой длины 1D проводника ![]() , приводит к тому, что
, приводит к тому, что ![]() в оказывается порядка
в оказывается порядка  . Аналогичную оценку
можно сделать и для
. Аналогичную оценку
можно сделать и для ![]()
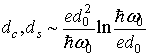 (47)
(47)
Теперь мы можем найти постоянный во времени вклад в средний квадрат флуктуаций
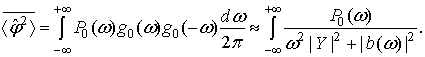 (48)
(48)
Характерная
частота при малых ![]() оказывается
порядка
оказывается
порядка ![]() , и c
логарифмической точностью интегрирование дает уравнение самосогласования
, и c
логарифмической точностью интегрирование дает уравнение самосогласования
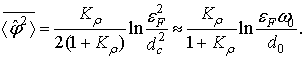 (49)
(49)
Решая уравнение самосогласования, получаем
 (50)
(50)
Видно,
что в отличие от стационарного режима критическое значение ![]() , при котором флуктуации
становятся бесконечными равно
, при котором флуктуации
становятся бесконечными равно ![]() . Кроме того, результат отличается и от результата,
полученного в работе [9], где критическое значение постоянной взаимодействия
. Кроме того, результат отличается и от результата,
полученного в работе [9], где критическое значение постоянной взаимодействия ![]() в динамическом режиме
электронного транспорта через примесь оказалось равным
в динамическом режиме
электронного транспорта через примесь оказалось равным ![]() .
.
Нам потребуется также выражение для ![]() в разложении
в разложении
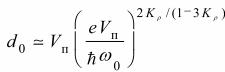 .
(51)
.
(51)
Теперь
мы можем перейти к нахождению ВАХ 1D проводника с неадиабатическими контактами.
Для этого рассмотрим уравнение для средних от операторов ![]() . Усредним термодинамически
уравнение
. Усредним термодинамически
уравнение
![]() (52)
(52)
Мы
считаем, что к левому электроду приложен потенциал ![]() , а к правому – потенциал
, а к правому – потенциал ![]() . Тогда
. Тогда ![]() и
и ![]() . Средние от выражений
. Средние от выражений ![]() и
и ![]() , соответствующих фриделевским осцилляциям,
равны
, соответствующих фриделевским осцилляциям,
равны
![]()
В результате уравнение на средние значения принимает вид
![]() (53)
(53)
Мы
будем решать это уравнение методом последовательных приближений, считая при ![]() слагаемые, отвечающие
за фриделевские осцилляции, малым возмущением. Во втором порядке теории
возмущений получаем, что ток
слагаемые, отвечающие
за фриделевские осцилляции, малым возмущением. Во втором порядке теории
возмущений получаем, что ток ![]() состоит из постоянной
состоит из постоянной ![]() и переменной
и переменной ![]() частей
частей
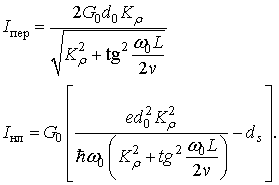 (54)
(54)
Осциллирующая зависимость от напряжения связана с отражениями от генерируемого импульса тока от контактов.
Заключение
В работе выведены граничные условия , которые позволяют описывать неидеальные контакты. Они являются обобщением граничных условий Эггера и Граберта [6], выведенных ранее для идеальных адиабатических контактов. Выведенные нами граничные условия отличаются от полученных в [6] также тем, что они позволяют включать в рассмотрение процессы релаксации из-за взаимодействия электронов с объемными электродами и позволяют корректно описывать флуктуации в 1D системе. Кроме того, показано, как граничные условия модифицируются при переменном приложенном напряжении.
Граничные
условия использованы для вычисления тока, протекающего через одномерную
систему, при приложении к контактам постоянной разности потенциала. Получено,
что межэлектронное взаимодействие и неидеальность контактов приводят к тому,
что проводимость 1D проводника уже не является омической и ВАХ уже не
описывается формулой Ландауэра ![]() . Из-за того, что неадиабатические
контакты представляют из себя неоднородность, вокруг них образуются
фриделевские осцилляции. Если приложенное напряжение ниже некоторого порогового
. Из-за того, что неадиабатические
контакты представляют из себя неоднородность, вокруг них образуются
фриделевские осцилляции. Если приложенное напряжение ниже некоторого порогового
![]() , то эти
фриделевские осцилляции существенно подавляют проводимость. В рассмотренном в
работе приближении мы получили, что ток в подпороговом режиме обращался в нуль,
но это связано с тем, что мы не учитывали флуктуации солитонного типа, т.е.
возможность макроскопического туннелирования, что привело бы к какому-то
ненулевому, но всё же малому значению тока.
, то эти
фриделевские осцилляции существенно подавляют проводимость. В рассмотренном в
работе приближении мы получили, что ток в подпороговом режиме обращался в нуль,
но это связано с тем, что мы не учитывали флуктуации солитонного типа, т.е.
возможность макроскопического туннелирования, что привело бы к какому-то
ненулевому, но всё же малому значению тока.
В
случае же, если приложено напряжение выше порогового и межэлектронное отталкивание
достаточно сильно ![]() ,
движение фриделевских осцилляций приводит к тому, что постоянная компонента
тока сопровождается переменной компонентой, осциллирующей с частотой
,
движение фриделевских осцилляций приводит к тому, что постоянная компонента
тока сопровождается переменной компонентой, осциллирующей с частотой ![]() . Эффект напоминает
динамический режим проводимости в эффекте Джозефсона и кулоновской блокаде.
Эффект подавляется флуктуациями при высоких температурах
. Эффект напоминает
динамический режим проводимости в эффекте Джозефсона и кулоновской блокаде.
Эффект подавляется флуктуациями при высоких температурах ![]() и в коротких проводниках
и в коротких проводниках ![]() . Эффект генерации и
нелинейная ВАХ возникают из-за межэлектронного взаимодействия в 1D электронной
системе. В отсутствие взаимодействия ВАХ линейна с проводимостью, равной
кванту проводимости
. Эффект генерации и
нелинейная ВАХ возникают из-за межэлектронного взаимодействия в 1D электронной
системе. В отсутствие взаимодействия ВАХ линейна с проводимостью, равной
кванту проводимости ![]() .
.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (контракт № 16.513.11.3066).
ЛИТЕРАТУРА
1. Kane C.L., Fisher M.P.A // Phys. Rev. Lett. 1992 V.68. No8. P.1220.
2. Giamarchi T. Quantum Physics in One Dimension. Oxford: Clarendon Press, 2003.
3. Auslaender O.M., Steinberg H., Yacoby A. et al. // Science 2005 V.308. No 5718. P. 88.
4. Ishii H., Kataura H., Shiozawa H. et al. // Nature 2003 V. 426. No 6966. P. 540.
5. Artemenko S.N., Remizov S.V., Shapiro D.S. // Письма в ЖЭТФ 2009. V.87. No 12. P. 792.
6. Egger R., Grabert H. // Phys. Rev. Lett. 1998. Vol. 80. No 10. P. 2255.
7. Grabert H. Exotic States in Quantum Nanostructures / Ed. by S. Sarkar. Dordrecht:
Kluwer, 2003. P.1.
8. Blanter Ya. M., Büttiker M. // Phys. Rep. 2000. V. 336. No 1-2. P. 1.
9. Artemenko S.N., Shapiro D.S., Vakhitov R.R., Remizov S.V. // J.Phys.:Conf. Ser. 2009. V.193. No 1. P. 012119.
 (10)
(10) 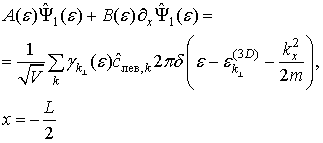 (11)
(11)
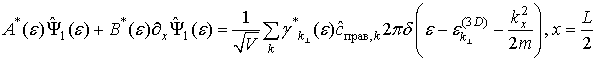 (12)
(12)  (14)
(14)
 (15)
(15)
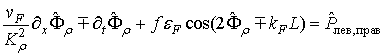 (18)
(18)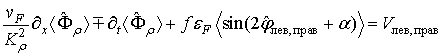 (20)
(20)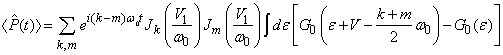 (25)
(25) (28)
(28)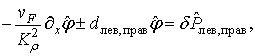 (29)
(29) (30)
(30)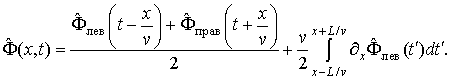 (34)
(34) (40)
(40)