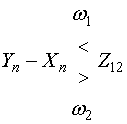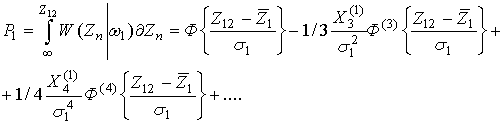УДК 621.391
АДАПТИВНАЯ КЛАССИФИКАЦИЯ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ ПО ПОЛЯРИЗАЦИОННЫМ ПАРАМЕТРАМ
Н. С. Акиншин, А. В. Болдин, А. В. Хомяков
ОАО Центральное конструкторское бюро аппаратостроения, г. Тула
Получена 26 октября 2011 г.
Аннотация. Определено решающее правило классификации радиолокационного сигнала на фоне гауссовской помехи по отношению собственных поляризаций цели. Синтезировано устройство адаптивной классификации, проведена оценка его эффективности.
Ключевые слова: классификация цели, радиолокационный сигнал, поляризационные параметры, отношение правдоподобия, поляризационный базис.
Abstract. A decision rule for classification of a radar signal against Gaussian noise according to relation of а target own polarizations is determined. An adaptive classification device is synthesized, its performance estimation is executed.
Keywords: target classification, radar signal, polarization parameters, likelihood ratio, polarization ratio.
Введение
Для классификации целей на фоне помех от подстилающей поверхности, требуется проведение сложных измерений параметров матрицы рассеяния, которые должны выполняться на интервалах времени, не превышающих времени перегруппировки центров рассеяния цели.
Известно, что с заданной матрицей рассеяния цели связано некоторое множество оптимальных поляризаций, к которым относятся нули перекрестной и совпадающей поляризаций [1,2]. Их относительное положение на сфере Пуанкаре инвариантно относительно поляризационного базиса. В частности, поляризационно инвариантна вилка, соединяющая точки нулевых поляризаций с точкой, соответствующей первой собственной поляризации цели (дескриптор Хьюнена G1). При этом величина угла, образованного этой вилкой, служит мерой способности цели поляризовать падающую волну и, исходя из результатов экспериментальных исследований, приведенных в [3,4], может быть использована для классификации целей.
Для уменьшения влияния помех от подстилающей поверхности на достоверность распознавания целесообразно использовать адаптивную настройку классификатора к известным характеристикам отраженного сигнала и помехи. В настоящей работе определяются алгоритм и характеристики адаптивной классификации сложной многоточечной цели, наблюдаемой на фоне подстилающей поверхности при использовании полного поляризационного приема. В качестве признака классификации рассматривается дескриптор цели G1.
Полагая, что в процессе обучения может быть определен собственный поляризационный базис цели, матрица рассеяния ωj, j = 1, … n класса цели может быть приведена к диагональному виду [1]
где λ(j)1,2 – собственное значение матрицы.
Угол Gi(j), характеризующий положение нулей на поляризационной вилке может быть определен, если известны сигналы с выходов амплитудных детекторов в ортогональных каналах, соответствующих первой и второй собственным поляризациям цели из соотношения
Здесь 0 ≤ G1 ≤ 45o [2].
Пусть цель состоит из "m" групп "блестящих" точек, огибающая сигнала от каждой из которых подчиняется распределению Рэлея. Средняя мощность сигнала, отраженного от цели в каждом из каналов, является величиной случайной и может быть распределена равномерно в интервале ΔΩl(j), l=1,2 для каждого из ωj классов целей. В этом случае мгновенное значение мощности сигнала в l-ом канале при измерении в собственном поляризационном базисе j-го класса целей, как это показано в
[5], будет описываться гамма распределением с неизвестным параметром Ωl(j) и параметром формы ml(j). Помеху в каждом из l каналов будем считать гауссовской функцией, некоррелированной с сигналом в совпадающие моменты времени, и с неизвестной интенсивностью σn12(j), которая может быть оценена в каждом из каналов на этапе обучения в соседних элементах дальности. С учетом сделанных предположений, распределение собственных чисел матрицы (1) для ωj класса целей в первом канале можно представить в следующем виде
где 1F1(*) -
вырожденная гипергеометрическая функция, ![]() .
.
Определение решающего правила для классификации
Одним из способов преодоления априорной неопределенности при решении задачи распознавания является оценка параметров распределения собственных чисел матрицы (1). Параметры W1(j) могут быть оценены методом максимального правдоподобия, однако это приводит к большому объему вычислений, поэтому воспользуемся оценками, полученными в [6] методом моментов:
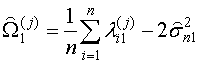 ,
,
где ![]() , Т – интервал
наблюдения цели; Dt – интервал
дискретизации случайного процесса l1(j)(t), равный в общем случае периоду повторения
зондирующих импульсов. Здесь и в дальнейшем подразумевается, что интервал
дискретизации процесса l1(j)(t), больше
интервала его корреляции. Воспользовавшись методом моментов [6], получим оценку
отношения сигнал/помеха в 1-м канале для j-го класса
цели:
, Т – интервал
наблюдения цели; Dt – интервал
дискретизации случайного процесса l1(j)(t), равный в общем случае периоду повторения
зондирующих импульсов. Здесь и в дальнейшем подразумевается, что интервал
дискретизации процесса l1(j)(t), больше
интервала его корреляции. Воспользовавшись методом моментов [6], получим оценку
отношения сигнал/помеха в 1-м канале для j-го класса
цели:
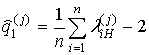
С учетом произведенных обозначений и соотношений (2), (3) распределение угла G1i для j-го класса цели можно представить в виде:
где ![]() ,
, 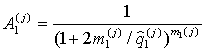 , i = 1,2; Г(k+2) - гамма-
функция, 2F1(.) – вырожденная
гипергеометрическая функция.
, i = 1,2; Г(k+2) - гамма-
функция, 2F1(.) – вырожденная
гипергеометрическая функция.
Оптимальная адаптивная процедура классификации сводится к сравнению логарифма отношения правдоподобия (ОП) lnL(G11,…,G1n) с переменным порогом C12. Здесь ОП L(G11,...,G1n) может быть записано в следующем виде:
где W1 (G1i|w1) определено соотношением (4).
В соответствии с (4), (5) решающее правило может быть представлено следующим образом:
Аргумент функции 2F1 является достаточно малой величиной, т.к. А2(j)<<1. Используя асимптотическое разложение функции 2F1(·) при малых значениях аргумента, соотношение (6) может быть сведено к более простой форме
Здесь
априорная информация ограничена значением параметра формы mi(j). Параметры ![]() ,
, ![]() определяются
на этапе обучения. В соотношении (7) величина переменного порога C12 может быть
найдена [7]
определяются
на этапе обучения. В соотношении (7) величина переменного порога C12 может быть
найдена [7]
где ![]() ;
; 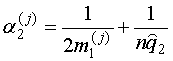 ,
, ![]() , l=1,2 -
отношение сигнал/шум в ортогональных каналах.
, l=1,2 -
отношение сигнал/шум в ортогональных каналах.
Подставляя (8) в (7), находим решающее правило для оптимального адаптивного классификатора
Принимаемые сигналы, соответствующие первой и второй собственным поляризациям цели в смеси с помехой, поступают на двухканальное устройство, коэффициенты передачи которого зависят от априорного значения характеристик цели mi(j) и от вычисляемых параметров сигнала и помехи qi(j). После весовой обработки и накопления по n-элементам выборки разность сигналов сравнивается с переменным порогом Z12, определяемым правой частью соотношения (9). Процесс адаптации включает две фазы:
а) оценку мощности помехи в тех элементах дальности, где сигнал отсутствует, и средней мощности сигнала по выборке сигнала и помехи в каждом ортогональном канале;
б) согласование системы, основанное на оцененных величинах, осуществляемое выбором оптимальных весовых коэффициентов и порога.
Оценка вероятности ошибки классификации
Определим эффективность синтезированного алгоритма, для чего вычислим условные вероятности правильных решений при соблюдении первой (ω1) и второй (ω2) гипотезы. Представим соотношение (9) в виде :
где ![]() ; Хn — оставшаяся
часть левой части выражения (9).
; Хn — оставшаяся
часть левой части выражения (9).
Раскладывая
функции 2F1(•) в ряд по
степени аргумента (![]() ) и ограничиваясь конечным числом
членов R, после громоздких вычислений методом
характеристических функций получим:
) и ограничиваясь конечным числом
членов R, после громоздких вычислений методом
характеристических функций получим:
где
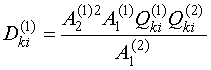 ;
;
 ;
;
 ;
;
 ;
;
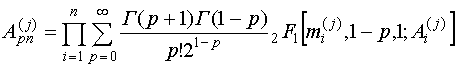 .
.
Проводя аналогичные вычисления для W(Xn|ωj), нетрудно прийти к следующей форме записи:
где
 ;
;
j=1,2.
Далее воспользовавшись соотношениями (11), (12) с учетом математических преобразований для разницы случайных величин получим распределение решающей статистики (9)
где
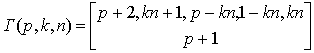 .
.
Полученное выражение относится к классу экспоненциальных распределений, что очевидно, является следствием многократного усреднения квадратов случайных величин λi, i=1,2. Указанное позволяет представить W(Zn) рядом Эджворта, в результате чего вероятность правильного решения, если верна первая гипотеза, определяется выражением
где Ф(х)
— интеграл вероятности, Фk(х) — к-ая
производная, ![]() , σ1,
—математическое ожидание и среднеквадратическое отклонение распределения (13), Хk —
семиинварианты. Аналогично при выполнении второй гипотезы
, σ1,
—математическое ожидание и среднеквадратическое отклонение распределения (13), Хk —
семиинварианты. Аналогично при выполнении второй гипотезы
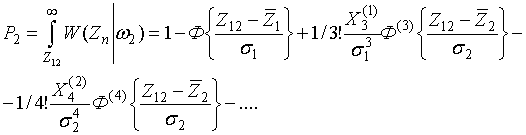 (15)
(15)
где Хk(2) — семиинварианты Zn при выполнении второй гипотезы. С помощью соотношений (11) - (13) нетрудно установить условия, при которых относительные величины семиинвариантов малы по сравнению с единицей. В этих условиях всеми поправками к нормальному распределению вероятности можно пренебречь и ограничиться в (14), (15) только первыми членами, т.е.
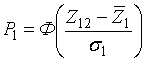 ,
,
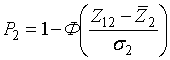 ,
(16)
,
(16)
Вероятности
1-Р1,2 построены на рис.1 для дивергенции параметров
классифицируемых целей ![]() (кривые 1 и 2); n=10, в
зависимости от усредненного по двум каналам отношения сигнал/шум
(кривые 1 и 2); n=10, в
зависимости от усредненного по двум каналам отношения сигнал/шум ![]() .
.

Рис.1. Вероятность правильного распознавания двух классов целей при использовании статистики нулевых поляризаций.
На
этом же рисунке показана кривая (3), построенная по (15), (16) при
неизвестных средних мощностях сигналов и помех в ортогональных каналах. Из
рисунка видно, что незнание мощности сигнала и помехи приводит к
заметному проигрышу в вероятности правильного распознавания, причем
проигрыш тем больше, чем больше ![]() . Из рисунка следует также очевидный
результат: увеличение дивергенции параметров классифицируемых целей (
. Из рисунка следует также очевидный
результат: увеличение дивергенции параметров классифицируемых целей (![]() ) уменьшает
вероятность ошибочных решений.
) уменьшает
вероятность ошибочных решений.
Выводы
Таким образом, для двухканального по поляризации приемного устройства получено решающее правило, по которому синтезирована структурная схема адаптивного классификатора двух классов целей при использовании информации о дескрипторе Хьюнена G1. Сравнение характеристик адаптивного классификатора с аналогичными характеристиками при неоцененных параметрах отраженного сигнала и помехи показывает, что возможен выигрыш в 13-14 дБ.
Литература
1. Huynen I., Rivhard H., Mcnolty F. Component distribution for fluctuating radar targets // IEEE Trans. Aerospace and Electron. Syst. 1975. 11. N 6. p. 1316-1332.
2. Джули Д. Поляризационное разнесение в радиолокации //ТИИЭР. 1986. т. 74. № 2. - с. 6-34.
3. Николаев В.А., Румянцев В.Л. Оценка поляризационного состояния сигналов, отраженных от малоразмерных наземных объектов // Оборонная техника, №8. 1995. - с. 33-34.
4. Акиншин Н.С., Николаев В.А., Румянцев В.Л. Поляризационные характеристики земных покровов при расширенной матрице рассеяния // Оборонная техника. 1995. №8. - с. 28-31.
5. Акиншин Н.С., Быстров Р.П., Румянцев В.Л., Соколов А.В. Миллиметровая радиолокация: методы обнаружения негауссовских сигналов // Под ред. Р.П. Быстрова. М: Радиотехника. 2010. - 528 с.
6. Мелитицкий В.А., Акиншин Н.С., Румянцев В.Л. Оценка средней мощности сигнала с m – распределением при наличии нормальной помехи // Радиотехника и электроника. 1987. №12. - с.10-14.
7. Фомин Я.А., Тарловский Г.Р. Статистическая теория распознавания образов. М.: Радио и связь. 1986. - 164 с.
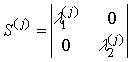
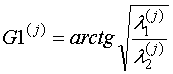 .
(2)
.
(2) (3)
(3)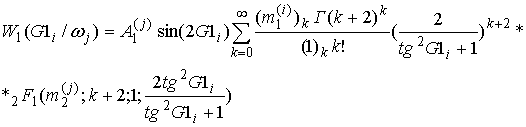 (4)
(4)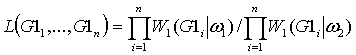 , (5)
, (5)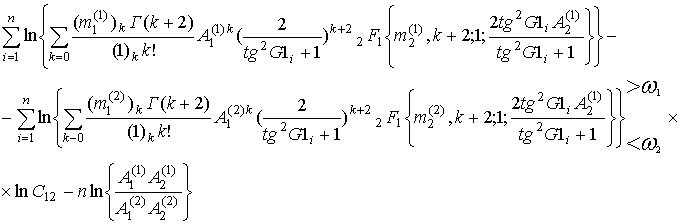
 . (7)
. (7)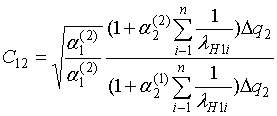
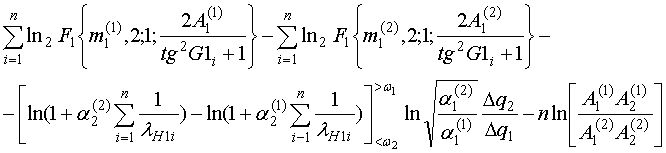 (9)
(9)