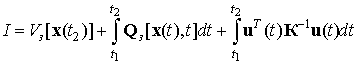УДК 629.7.058.53
ТРАЕКТОРНОЕ УПРАВЛЕНИЕ НАБЛЮДЕНИЕМ
В ПОДВИЖНЫХ ПАССИВНЫХ СИСТЕМАХ
ВОЗДУШНОГО БАЗИРОВАНИЯ
В. И. Меркулов, Д. А. Миляков, В. С. Чернов
ОАО «Концерн «Вега»
Получена 19 ноября 2012 г.
Аннотация. Рассмотрен вариант построения угломерной двухпозиционной распределенной радиоэлектронной системы управления воздушного базирования, для решения ряда практических задач, требующих непрерывного оценивания параметров источников радиоизлучений (ИРИ).
Предложен вариант организации управления приемной позицией информационной поддержки (ПП ИП) при условии минимизации ошибки определения местоположения ИРИ. Разработан алгоритм на основе теории оптимального управления динамическими процессами. Проведен анализ предложенного алгоритма. В работе также использован градиентный метод нелинейного программирования для определения оптимального управления ПП ИП. Проведено математическое моделирование. Представлены результаты его анализа.
Ключевые слова: траекторное управление наблюдением; боевая эффективность, живучесть, информативность; системные показатели БРЛС; тактические показатели РЛС; статистическая теория оптимального управления; первичная, вторичная обработка сигналов.
Abstract. A design of bistatic angle finder of spatially distributed airborne radio electronic control system is studied. The variant is intended for solution of a range of practical tasks which require continuous estimation of characteristics of radio sources. A variant of control of the receiving post of informational support with minimisation of localisation error of radio source is proposed. An algorithm is demonstrated based on statistical theory of optimal control of dynamic processes and its study is conducted. The gradient method of non-linear programming is used for obtaining optimal control of the receiving post of informational support. Results of a simulation are presented.
Keywords: trajectory control of observation, combat effectiveness, survivability, informativeness, system factors of onboard radar, tactical factors of radars, statistical theory of optimal control, secondary signal processing, non-linear programming.
Существует ряд задач народнохозяйственного и военного назначения, охраны государственной границы, проведения антитеррористических мероприятий, обеспечения действий в чрезвычайных ситуациях, требующих для своего решения непрерывного ведения мониторинга работы источников радиоизлучений, в процессе которого выполняются такие операции как поиск, обнаружение, распознавание, отождествление и определение местоположения источников радиоизлучений (ИРИ). Для решения указанных задач могут применяться распределенные угломерные радиоэлектронные системы управления воздушного базирования (РЭСУ ВБ), состоящие из пункта сбора, обработки информации и управления (ПОИУ) на базе воздушного командного пункта и подвижных приемных позиций (ПП), на которых осуществляется прием сигналов от ИРИ. Извлекаемая на каждой ПП из принимаемых сигналов информация транслируется по радиолиниям связи в ПОИУ и на другие ПП. На начальном этапе в ПОИУ производится коллективное распределение целей (задач) между ПП, необходимое для достижения общей групповой цели, и при необходимости разбиение всей совокупности ПП на отдельные группы.
Результаты решения задачи коллективного распределения целей передаются с ПОИУ через многоканальную командную радиолинию управления (КРУ) на ПП, базирующиеся на пилотируемых и беспилотных летательных аппаратах (ЛА). Далее начинается этап самостоятельного функционирования ПП, на котором осуществляется коллективная или стайная стратегия управления ими [1]. Коллективное управление ПП применяется при необходимости точного определения местоположения всех ИРИ в заданном географическом районе. Стратегия стайного управления используется в тех случаях, когда требуется обеспечить встречу назначенных ПП или объектов, запускаемых с ПП, с выбранными ИРИ.
Для формирования сигналов траекторного управления на ПП предварительно вырабатываются оценки относительных и абсолютных координат и параметров движения ИРИ. Особенность процедуры оценивания в рассматриваемых системах состоит в том, что точность оценивания фазовых координат ИРИ в существенной степени зависит от взаимного положения ПП и ИРИ, т.е. от геометрии решения задачи местоопределения цели. Установлено [2], что точность оценивания наиболее высока, если угол пересечения линий положения (пеленгов) ИРИ, измеряемых из двух точек, достаточно близок к прямому, и заметно снижается, если линии положения пересекаются под острым углом. Поэтому для достижения высокой эффективности функционирования распределенных угломерных (РУ) РЭСУ ВБ предпринимают определенные организационные мероприятия, направленные на построение требуемого взаимного положения ПП и ИРИ. Проведение этих мероприятий существенно упрощается при объединении ПП в отдельные пары. При этом на ПП, входящие в состав пары, может быть возложено решение разных задач. В частности, одна из ПП (ведущая) непосредственно решает задачу сближения и встречи с ИРИ, другая ПП — задачу информационной поддержки. В этом случае ведущая ПП управляется системой наведения по известным алгоритмам [3], которые выбираются в соответствие с поставленными целями сближения. Полет ПП информационной поддержки (ИП) организуется таким образом, чтобы обеспечить требуемое взаимное пространственное положение ИРИ и ПП. В результате образуется угломерная двухпозиционная радиоэлектронная система управления (УДП РЭСУ), которая, по терминологии, принятой в [1], представляет собой гетерогенный кластер. Кластеризация ПП на пары особенно целесообразна при реализации стратегии стайного управления в РУ РЭСУ.
Рассмотрим принцип функционирования РУ РЭСУ, используя для этого упрощенную структурную схему, представленную на рисунке 1. Для простоты на этом рисунке показана одна УДП РЭСУ, в общем случае таких систем может быть множество.

Рис. 1. Структурная схема распределенной угломерной радиоэлектронной системы управления с двумя приемными позициями
В состав УДП РЭСУ входят первая и вторая подвижные ПП. Каждая ПП содержит одинаковый состав оборудования: угломерное устройство, навигационную систему, аппаратуру передачи данных, приемную часть КРУ, вычислительную систему и систему автоматического управления (САУ).
Источник излучения, являющийся для наводимых ПП УДП РЭСУ радиоизлучающей целью, формирует радиосигналы, принимаемые в первой и второй ПП. Источниками радиоизлучения могут быть различные радиоэлектронные средства: бортовые и наземные РЛС, радиосвязные системы и др. Угломерные устройства измеряют бортовые пеленги ИРИ в каждой ПП. Навигационные системы счисляют местоположение ПП в прямоугольной системе координат и оценивают угловые положения ЛА в пространстве. Предпочтительным вариантом для определения координат ЛА является использование спутниковой радионавигационной системы как наиболее точной. Указанные координаты и параметры движения образуют минимально необходимый набор измеряемых величин. Оцененные значения пеленгов ИРИ, прямоугольных координат ПП, а также курсов и углов тангажа с помощью аппаратуры передачи данных передаются с ПП в ПОИУ и на другие ПП. Вместо пеленгов ИРИ, курсов и углов тангажа ПП могут передаваться функционально связанные с ними азимуты и углы места ИРИ. Кроме того, передаются радиотехнические параметры ИРИ, что необходимо для распознавания типов ИРИ и отождествления пеленгов. Результаты оценивания пеленгов ИРИ в двух позициях, прямоугольных координат и угловых положений ПП поступают в вычислительную систему ПОИУ, в которой на начальном этапе происходит отождествление пеленгов и формирование оценок координат ИРИ и параметров их движения. В ПОИУ определяется также тип ИРИ. При отождествление пеленгов и определении типов ИРИ может использоваться информация, поступающая от других ПП.
На основе поступившей информации в ПОИУ производится общая оценка радиоэлектронной обстановки, кластеризация ПП, распределение различных ИРИ по отдельным парам ПП (кластерам). На основе заложенных в вычислительную систему ПОИУ критериев назначения выбираются ведущая ПП и ПП ИП, обеспечивающая наилучшие условия наблюдения ИРИ. Кроме того, выбираются режимы функционирования пеленгаторов.
Следует отметить, что указанная проблема коллективного распределения целей относится к широко известной задаче о назначениях, которая может решаться с использованием как точных, так и приближенных алгоритмов [1]. Данные коллективного целераспределения, относящие к каждой ПП, передаются через многоканальную КРУ. КРУ состоит из передающей части, установленной в ПОИУ, и приемных частей, размещенных на ПП. В последующем ПОИУ осуществляет общий контроль качества и эффективности функционирования РУ РЭСУ ВБ в целом.
На этапе самостоятельной работы УДП РЭСУ приемные позиции обмениваются результатами измерений пеленгов ИРИ и собственных прямоугольных координат, характеризующих местоположение ПП. На их основе в вычислительных системах ПП формируются координаты и параметры движения назначенного с ПОИУ источника радиоизлучения и вырабатываются параметры управления согласно поставленным задачам (ведущая позиция или позиция информационной поддержки) и выбранному способу наведения. Параметры управления, воздействуя на системы автоматического управления, изменяют траектории движения носителей ПП таким образом, чтобы обеспечивалось решение целевой задачи кластера.
Как указывалось выше, высокая точность определения фазовых координат ИРИ может быть достигнута за счет оптимизации траекторного управления ПП ИП, в результате целенаправленного движения которой обеспечивается минимизация ошибок местоопределения ИРИ. Выполним синтез алгоритмов траекторного управления ПП ИП для горизонтальной плоскости наведения. При этом для простоты полагаем, что движение ПП УДП РЭСУ в вертикальной плоскости выполняется на одинаковой для обеих ПП постоянной высоте. Кроме того, рассматривается случай, когда значения углов визирования ИРИ в вертикальной плоскости малы.
Как известно [2, 3],
принцип определения координат ИРИ в УДП РЭСУ в горизонтальной плоскости при
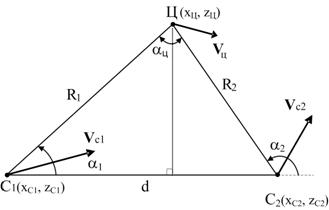
указанных условиях состоит в следующем (рис. 2). При пеленгации ИРИ,
расположенного в точке Ц, из двух точек С1 и С2,
отстоящих друг от друга на расстоянии ![]() ,
координаты ИРИ в УДП РЭСУ определяются путем решения треугольника С1ЦС2
по двум углам
,
координаты ИРИ в УДП РЭСУ определяются путем решения треугольника С1ЦС2
по двум углам ![]() ,
, ![]() и
основанию
и
основанию ![]() с помощью следующих соотношений [2]:
с помощью следующих соотношений [2]:
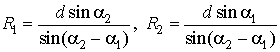 , (1)
, (1)
где углы ![]() и
и ![]() отсчитываются в точках С1 и С2
относительно направления базы пеленгации.
отсчитываются в точках С1 и С2
относительно направления базы пеленгации.
Рис. 2. Геометрия взаимного расположения приемных позиций и источника радиоизлучения
На
рисунке введены следующие обозначения: ![]() и
и ![]() — расстояния от ИРИ
(точка Ц) до ПП С1 и С2, оборудованных
пеленгаторами;
— расстояния от ИРИ
(точка Ц) до ПП С1 и С2, оборудованных
пеленгаторами; ![]() — бистатический угол (угол
пересечения линий визирования);
— бистатический угол (угол
пересечения линий визирования); ![]() — база
пеленгации (линия, соединяющая ПП);
— база
пеленгации (линия, соединяющая ПП); ![]() ,
, ![]() ,
, ![]() —
векторы скоростей ПП и ИРИ;
—
векторы скоростей ПП и ИРИ; ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() — текущие
координаты первой (ведущей) и второй (информационной поддержки) ПП и
ИРИ.
— текущие
координаты первой (ведущей) и второй (информационной поддержки) ПП и
ИРИ.
Наряду
с оцениванием расстояний ![]() и
и ![]() в УДП РЭСУ может выполняться
оценивание прямоугольных координат
в УДП РЭСУ может выполняться
оценивание прямоугольных координат ![]() ,
, ![]() ИРИ [4, 5].
ИРИ [4, 5].
В УДП
РЭСУ ошибки измерителей азимутов
ИРИ ![]() и
и ![]() относительно
двух ПП и ошибки измерения собственных прямоугольных координат ПП приводят к
погрешностям формирования (расчета) оценок расстояний
относительно
двух ПП и ошибки измерения собственных прямоугольных координат ПП приводят к
погрешностям формирования (расчета) оценок расстояний ![]() и
и
![]() и прямоугольных координат
и прямоугольных координат ![]() и
и ![]() ИРИ.
Анализ точности определения местоположения ИРИ при функционировании УДП РЭСУ,
проведенный в [2], показал, что ошибки определения местоположения ИРИ зависят
от «геометрии» системы местоопределения, т.е. от размеров базы и положения ИРИ
относительно базы, от погрешностей измерения пеленгов, прямоугольных координат
и курсов ПП.
ИРИ.
Анализ точности определения местоположения ИРИ при функционировании УДП РЭСУ,
проведенный в [2], показал, что ошибки определения местоположения ИРИ зависят
от «геометрии» системы местоопределения, т.е. от размеров базы и положения ИРИ
относительно базы, от погрешностей измерения пеленгов, прямоугольных координат
и курсов ПП.
Точность
определения местоположения радиоизлучающих целей на плоскости характеризуется
линейной ошибкой. При случайных ошибках пеленгации
в случае одинаковых ошибок пеленгаторов ![]() для
СКО местоопределения
для
СКО местоопределения ![]() имеет место соотношение [2]:
имеет место соотношение [2]:
Из (2) следует, что
ошибка ![]() определяется значениями
определяется значениями ![]() ,
, ![]() и
и
![]() и ошибками пеленгации
и ошибками пеленгации ![]() .
.
На основе анализа выражения (2) могут быть выработаны рекомендации по требуемым параметрам геометрической конфигурации ПП на плоскости, для достижения которых разработаны различные способы траекторного управления ПП [6-13]. Так как ведущая ПП решает задачу сближения с ИРИ, то полет ПП ИП организуется таким образом, чтобы обеспечить требуемое для высокоточного функционирования УДП РЭСУ взаимное геометрическое положение ИРИ и ПП.
Как видно из формулы (2),
одним из способов снижения ошибок оценивания местоположения ИРИ является
поддержание угла ![]() , близким к 90о. Для
реализации этого условия разработано несколько способов наведения ЛА в УДП РЭСУ
[8-13].
, близким к 90о. Для
реализации этого условия разработано несколько способов наведения ЛА в УДП РЭСУ
[8-13].
Общим недостатком данных способов наведения является тот факт, что до выхода ПП ИП в точку, лежащую на перпендикуляре к линии «ИРИ – ведущая ПП», или в заданную точку этого перпендикуляра не предъявляется никаких требований к текущим значениям ошибок определения местоположения ИРИ. В то же время процесс наведения ведущей ПП может закончиться еще до момента выхода ПП ИП на указанный перпендикуляр, когда ошибки определения местоположения ИРИ становятся минимальными.
Так как процедура обеспечения одновременного выхода ведущей ПП в точку окончания наведения, а ПП ИП на заданную линию (точку) представляет собой довольно сложную задачу, то управление ПП ИП можно организовать таким образом, чтобы ошибка определения местоположения ИРИ в любой момент времени была минимально возможной. Для выполнения данного условия ПП ИП должна двигаться по специальной траектории, параметры которой определяются алгоритмом, полученным на основе теории оптимального управления (ТОУ) динамическими процессами. В качестве целевой функции при этом может быть выбрана зависимость ошибки (2) определения местоположения ИРИ от погрешностей пеленгаторов и «геометрии» решения задачи местоопределения.
Для вычисления оптимальных траекторий могут использоваться две группы методов:
– косвенные методы, использующие необходимые условия оптимальности;
– прямые методы, определяющие оптимальное управление непосредственным решением оптимизируемого функционала без использования необходимых условий.
Из косвенных методов наибольшее распространение получили принцип максимума Л.С. Понтрягина и динамическое программирование Беллмана. При этом следует отметить, что разработанная до настоящего времени техника оптимизации, позволяющая получить аналитически оптимальное управление из необходимых условий, применима к ограниченному типу задач.
Рассмотрим возможности применения ТОУ на базе принципа динамического программирования для разработки алгоритмов траекторного управления ПП ИП в УДП РЭСУ. Предварительно приведем необходимые математические соотношения [14].
Пусть управляемый процесс описывается детерминированным уравнением общего вида:
![]() .
.
Здесь ![]() —
полная производная вектора состояния
—
полная производная вектора состояния ![]() по времени
по времени ![]() ,
, ![]() —
векторная функция векторных аргументов
—
векторная функция векторных аргументов ![]() и
скалярного аргумента
и
скалярного аргумента ![]() ,
, ![]() —
вектор управления.
—
вектор управления.
Как известно, для вычисления оптимального управления с использованием принципа динамического программирования решается уравнение Беллмана. Решение этого уравнения упрощается в определенных случаях, в частности, для процесса с линейно входящим управлением
![]() (3)
(3)
и интегрального квадратичного функционала качества [14]:
где ![]() —
заданная скалярная функция конечного состояния процесса
—
заданная скалярная функция конечного состояния процесса ![]() ;
;
![]() — заданная квадратичная функция,
определяющая текущую точность управления; К — диагональная невырожденная
матрица заданных коэффициентов штрафов за экономичность сигналов управления;
— заданная квадратичная функция,
определяющая текущую точность управления; К — диагональная невырожденная
матрица заданных коэффициентов штрафов за экономичность сигналов управления; ![]() — матричная функция размера
— матричная функция размера ![]() аргументов
аргументов ![]() ,
, ![]() .
.
Интегрирование в (4)
осуществляется от текущего момента времени ![]() до
конечного
до
конечного ![]() . Первая часть функционала, называемая
терминальной, отражает конечную ошибку, вторая — требования к точностным характеристикам
системы и третья — ограничения на сигналы управления.
. Первая часть функционала, называемая
терминальной, отражает конечную ошибку, вторая — требования к точностным характеристикам
системы и третья — ограничения на сигналы управления.
Уравнение Беллмана и оптимальное управление имеют вид [14]:
 (5)
(5)
Здесь «![]() » — символ транспонирования.
» — символ транспонирования.
Уравнение Беллмана
представляет собой нелинейное уравнение в частных производных. Решение этого
уравнения при граничном ![]() условии
условии ![]() должно определять оптимальное управление.
Аналитическое построение точных решений существуют лишь для
линейно-квадратичных задач. Для нелинейных систем возможны различные способы
приближенного решения уравнений Беллмана, которые могут оказаться полезными при
решении задач синтеза для динамических процессов невысокой размерности. При
этом используют численную форму динамического программирования, построение
разностных схем, метод рядов и метод характеристик [14].
должно определять оптимальное управление.
Аналитическое построение точных решений существуют лишь для
линейно-квадратичных задач. Для нелинейных систем возможны различные способы
приближенного решения уравнений Беллмана, которые могут оказаться полезными при
решении задач синтеза для динамических процессов невысокой размерности. При
этом используют численную форму динамического программирования, построение
разностных схем, метод рядов и метод характеристик [14].
В общем случае, управляемый процесс является стохастическим. Следует заметить, что для нелинейных систем задача управления стохастическими процессами путем минимизации функционалов намного сложнее, чем для детерминированных процессов. В то же время для нелинейных задач применительно к функционалу (4) приближенно справедлива теорема разделения [14], согласно которой можно раздельно синтезировать систему оценивания и идентификации и систему собственно управления. Ниже предполагается, что процедура оценивания фазовых координат и идентификации параметров в УДП РЭСУ произведена.
Конкретизируем постановку задачи нахождения оптимального управления применительно к приемной позиции ИП УДП РЭСУ. В качестве целевой функции выберем ошибку (2) определения местоположения ИРИ
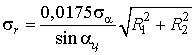 ,
,
где
![]() —
площадь треугольника С1ЦС2 (рис. 2),
—
площадь треугольника С1ЦС2 (рис. 2), ![]() — полупериметр этого треугольника,
— полупериметр этого треугольника, ![]() — расстояние между ПП (база пеленгации),
— расстояние между ПП (база пеленгации), ![]() ,
,
![]() — текущие
прямоугольные координаты ведущей ПП.
— текущие
прямоугольные координаты ведущей ПП.
Введем обозначения
переменных вектора состояния х, полагая в качестве управления ![]() угол
угол ![]() отклонения
элеронов и учитывая связи угла
отклонения
элеронов и учитывая связи угла![]() с углами отклонения
элеронов и курса ЛА [3]:
с углами отклонения
элеронов и курса ЛА [3]: ![]() — прямоугольные
координаты ведущей ПП по оси
— прямоугольные
координаты ведущей ПП по оси ![]() неподвижной в
пространстве горизонтальной системы координат
неподвижной в
пространстве горизонтальной системы координат ![]() ;
; ![]() — производная по времени прямоугольной
координаты ведущей ПП по оси
— производная по времени прямоугольной
координаты ведущей ПП по оси ![]() ;
; ![]() — прямоугольные координаты ПП ИП по
оси
— прямоугольные координаты ПП ИП по
оси ![]() ;
; ![]() —
производная по времени прямоугольной координаты ПП ИП по оси
—
производная по времени прямоугольной координаты ПП ИП по оси ![]() ;
; ![]() — курс
ПП ИП
— курс
ПП ИП ![]() ;
; 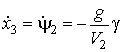 —
скорость изменения курса ПП ИП
—
скорость изменения курса ПП ИП ![]() ;
; ![]() — крен ПП ИП
— крен ПП ИП ![]() ;
;
![]() — скорость изменения угла крена;
— скорость изменения угла крена; ![]() и
и ![]() —
коэффициент эффективности и угол отклонения элеронов.
—
коэффициент эффективности и угол отклонения элеронов.
Отсюда следует, что уравнения состояния можно записать следующим образом:
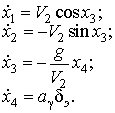 (8)
(8)
Применительно к рассматриваемому случаю минимизируемый функционал (4) имеет вид:
 (9)
(9)
где
![]() ,
, ![]() ,
, ![]() — коэффициенты штрафов.
— коэффициенты штрафов.
В минимизируемом
функционале (9) член с квадратичным управлением ![]() служит
для ограничения управляющего воздействия.
служит
для ограничения управляющего воздействия.
Если рассматривать в
качестве управления ![]() боковое ускорение
боковое ускорение ![]() , то уравнения состояния могут быть
упрощены. Действительно, скорость изменения курса ПП
, то уравнения состояния могут быть
упрощены. Действительно, скорость изменения курса ПП ![]() [3]
[3]
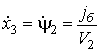 .
.
Для этого случая уравнения состояния приобретают вид:
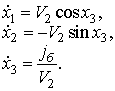 (10)
(10)
Из (10) видно, что
размерность вектора состояния ![]() меньше, чем в динамической
системе (8). Минимизируемый функционал имеет тот же вид (9), но при условии подстановки
меньше, чем в динамической
системе (8). Минимизируемый функционал имеет тот же вид (9), но при условии подстановки
![]() вместо
вместо ![]() .
.
Поскольку в
минизируемом функционале СКО местоопределения ![]() нелинейно
зависит от прямоугольных координат, то аналитическое определение оптимального
управления не представляется возможным. Для отыскания оптимального управления ПП
ИП необходимо воспользоваться указанными выше приближенными способами решения
задачи.
нелинейно
зависит от прямоугольных координат, то аналитическое определение оптимального
управления не представляется возможным. Для отыскания оптимального управления ПП
ИП необходимо воспользоваться указанными выше приближенными способами решения
задачи.
Рассмотрим возможности прямых методов оптимизации для нахождения алгоритма траекторного управления ПП ИП.
В классе прямых методов наиболее популярны градиентные методы. Из классических градиентных методов наиболее известны метод наискорейшего спуска и метод Ньютона-Рафсона. Ко второму поколению градиентных методов относятся метод сопряженного градиента и метод с переменной метрикой, которые характеризуются простотой и хорошей сходимостью. Оптимальное управление при использовании прямых методов является итерационной процедурой, основанной на информации о градиенте функционала качества.
При разработке алгоритмов траекторного управления по курсу для ПП ИП на основе прямых методов параметры траектории приемной позиции ИП могут рассчитываться по формулам, полученным на основе теории принятия решений в одношаговых задачах оптимального управления с использованием градиентных методов нелинейного программирования [15]. В качестве целевой функции целесообразно выбрать ошибку (2). В этом случае движение по требуемой траектории ПП ИП приводит к максимально быстрому уменьшению ошибок местоопределения ИРИ на каждом шаге управления.
Стратегия градиентного способа представляет собой последовательность шагов, каждый из которых содержит две операции:
1) определение направления наибольшей крутизны спуска в текущей точке;
2) перемещение в выбранном направлении на заданное расстояние.
Следует отметить, что при
определении направления наибольшей крутизны спуска используется СКО ![]() (2). В то же время управляемыми переменными
состояния (компонентами вектора состояния) являются прямоугольные координаты
(2). В то же время управляемыми переменными
состояния (компонентами вектора состояния) являются прямоугольные координаты ![]() ,
,
![]() ПП ИП
ПП ИП ![]() . Выражение (2) в явном виде не зависит от
этих координат, поэтому его преобразуют к виду, удобному для нахождения
градиента целевой функции, используя соответствующие уравнения связи (6) и (7).
. Выражение (2) в явном виде не зависит от
этих координат, поэтому его преобразуют к виду, удобному для нахождения
градиента целевой функции, используя соответствующие уравнения связи (6) и (7).
При
подстановке (6) и (7) в (2) получают зависимость целевой функции от
прямоугольных координат ИРИ и ПП. Далее вычисляют градиент целевой функции, для
чего находят частные производные ![]() и
и ![]() целевой функции
целевой функции ![]() по
прямоугольным координатам
по
прямоугольным координатам ![]() ,
, ![]() ПП ИП
ПП ИП ![]() .
После вычисления частных производных требуемый курс ПП ИП и параметр управления
ею рассчитывают в ПП ИП соответственно по формулам
.
После вычисления частных производных требуемый курс ПП ИП и параметр управления
ею рассчитывают в ПП ИП соответственно по формулам
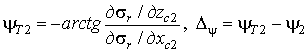 , (11)
, (11)
где ![]() —
фактический (текущий) курс ПП ИП.
—
фактический (текущий) курс ПП ИП.
Управление
ПП ИП осуществляется таким образом, чтобы значение параметра управления ![]() стремилось к нулю.
стремилось к нулю.
Алгоритм
(11) траекторного управления ПП ИП обеспечивает получение наибольшей скорости
убывания СКО местоопределения ИРИ.
Достоинство данного алгоритма состоит в том, что убывание СКО
местоопределения ИРИ обеспечивается не только за счет изменения угла ![]() , но и в результате уменьшения расстояний
, но и в результате уменьшения расстояний
![]() и
и
![]() .
.
Для
оценки эффективности разработанного способа и алгоритма траекторного управления
ПП ИП было проведено математическое моделирование процесса наведения ПП,
входящих в состав УДП РЭСУ.
В качестве показателя эффективности рассматривалась ошибка ![]() (2). При моделировании полагалось, что
ИРИ движется
равномерно и прямолинейно. Ведущая ПП наводится на цель по методу перехвата [3].
Приемная позиция ИП управляется согласно градиентному способу.
(2). При моделировании полагалось, что
ИРИ движется
равномерно и прямолинейно. Ведущая ПП наводится на цель по методу перехвата [3].
Приемная позиция ИП управляется согласно градиентному способу.
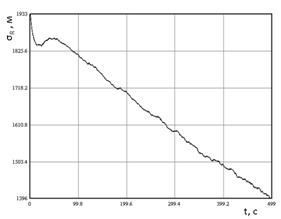
Результаты
моделирования приведены на рисунках 3, 4. На рисунке 3 показаны траектории
движения ведущей ПП ![]() , ПП ИП
, ПП ИП ![]() ,
ПОИУ и ИРИ в горизонтальной плоскости для одного из гипотетических вариантов
применения, а на рисунке 4 — график поведения во времени СКО
,
ПОИУ и ИРИ в горизонтальной плоскости для одного из гипотетических вариантов
применения, а на рисунке 4 — график поведения во времени СКО ![]() определения местоположения ИРИ.
определения местоположения ИРИ.
|
|
|
|
Рис. 3. Геометрия задачи траекторного управления наблюдением |
Рис. 4. Зависимость СКО определения местоположения ИРИ от времени |
В процессе моделирования проверялось влияние ошибок измерения азимутов ИРИ на качество наведения и ошибки определения местоположения ИРИ. При реальных ошибках измерения это влияние оказалось незначительным и приводит лишь к небольшим флуктуациям траекторий полета наводимых ПП (рис. 4).
Анализ результатов моделирования показывает, что применение предлагаемого способа траекторного управления позволяет успешно решать стоящие перед УДП РЭСУ задачи.
Следует отметить, что градиентный
метод может быть применен для построения требуемой геометрии взаимного
положения ПП, когда положение наводимых ПП по отношению к ИРИ задается
бистатическим углом ![]() (рис. 2). В этом случае
минимизируемый функционал (4) может быть задан в виде:
(рис. 2). В этом случае
минимизируемый функционал (4) может быть задан в виде:
![]()
где ![]() и
и ![]() — заданное и текущее значения
бистатического угла.
— заданное и текущее значения
бистатического угла.
На практике возможны
ситуации, когда требуется обеспечить сближение ПП с ИРИ под заданным углом подхода.
Для решения данной задачи могут быть использованы разработанные ранее методы и
алгоритмы, приведенные в [7-13]. При этом для вычисления угла ![]() вместо координат ведущей ПП следует подставить
координаты некоторой виртуальной точки, которая совместно с ИРИ определяет
положение линии отсчета указанного угла в пространстве. Тем самым, появляется
возможность обеспечения выхода нескольких ПП с разных направлений на ИРИ, что
иногда требуется при выполнении групповых действий.
вместо координат ведущей ПП следует подставить
координаты некоторой виртуальной точки, которая совместно с ИРИ определяет
положение линии отсчета указанного угла в пространстве. Тем самым, появляется
возможность обеспечения выхода нескольких ПП с разных направлений на ИРИ, что
иногда требуется при выполнении групповых действий.
Выводы
1. Разработанные оптимальные алгоритмы траекторного управления на основе принципа динамического программирования и градиентного метода наискорейшего спуска обеспечивают полет приемной позиции информационной поддержки по траектории, позволяющей получить минимально возможные ошибки определения местоположения ИРИ в любой момент времени. Эти же алгоритмы могут применяться при наведении приемных позиций в случае, когда необходимо поддерживать требуемые значения бистатических углов визирования приемных позиций с ИРИ.
2. Для обеспечения в процессе сближения требуемого угла подхода приемной позиции к ИРИ возможно использование разработанных ранее применительно к угломерным двухпозиционным системам радиоуправления методов и алгоритмов наведения летательных аппаратов за счет их достаточно простой модификации. В результате может быть осуществлено групповое сближение нескольких приемных позиций с ИРИ с разных угловых направлений.
Литература
1. Каляев И.А., Гайдук А.Р., Капустян С.Г. Модели и алгоритмы коллективного управления в группах роботов. — М.: ФИЗМАТЛИТ, 2009.
2. Верба В.С., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч.3. / Под ред. В.С. Вербы и В.И. Меркулова. — М.: Радиотехника, 2010.
3. Авиационные системы радиоуправления: учебник для военных и гражданских ВУЗов и научно-исследовательских организаций. / В.И. Меркулов, В.С. Чернов, В.А. Гандурин, В.В. Дрогалин, А.Н. Савельев. / Под ред. В.И. Меркулова. — М.: Изд. ВВИА им. проф. Н.Е. Жуковского, 2008.
4. Меркулов В.И., Чернов В.С., Юрчик И.А. Авиационные многопозиционные системы радиоуправления. // Успехи современной радиоэлектроники, 2006, № 12.
5. Абатуров В.А., Меркулов В.И., Чернов В.С. Авиационные системы радиоуправления. Многопозиционные системы радиоуправления. Учебное пособие. — М.: ВВИА им. проф. Н.Е Жуковского, 2008.
6. Меркулов В.И., Куимов А.М., Чернов В.С. Траекторное управление пассивными двухпозиционными системами. // Информационно-измерительные и управляющие системы, 2008, № 12, т.6.
7. Меркулов В.И., Харьков В.П., Чернов В.С. и др. Алгоритмы траекторного управления самолетами в угломерной двухпозиционной радиолокационной системе. Юбилейная научно-техническая конференция «Авиационные системы 21 века», ФГУП ГосНИИАС, 2006.
8. Меркулов В.И., Харьков В.П., Чернов В.С. Алгоритмы управления позициями в пассивной двухпозиционной радиолокационной системе. // Радиотехника, 2004, № 10.
9. Меркулов В.И. Управления пассивными двухпозиционными РЛС в режиме наведения на радиоизлучающую цель. // Радиотехника, 2005, № 6.
10. Бирина Н.О., Меркулов В.И., Чернов В.С. и др. Способ управления самолетами в угломерной двухпозиционной радиолокационной системе. // Радиотехника, 2005, № 6.
11. Способ наведения летательных аппаратов в двухпозиционной радиолокационной системе. Патент РФ на изобретение № 2262649 от 20.10.2005.
12. Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе. Патент РФ на изобретение № 2256870 от 20.07.2005.
13. Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе. Патент РФ на изобретение № 2308093 от 10.10.2007.
14. Справочник по теории автоматического управления / Под ред. А.А. Красовского. — М.: Наука. Гл. ред. физ.-мат. лит., 1987.
15. Коршунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов. Изд. 2-е, перераб. и доп. — М.: Энергия, 1980.