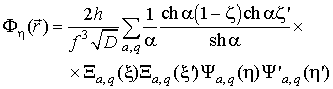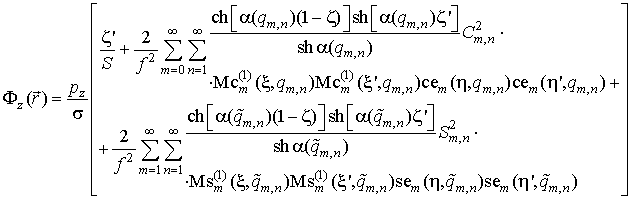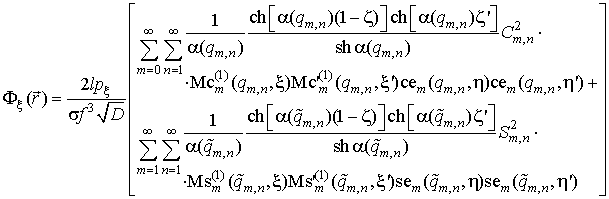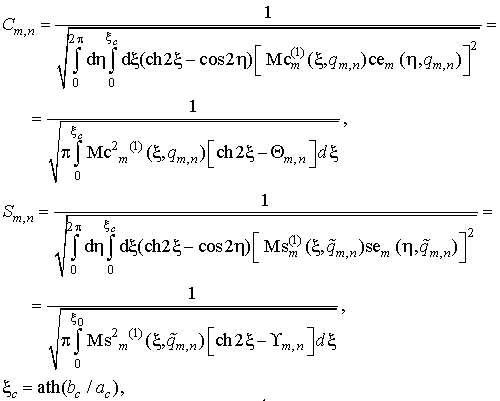Расчет электрических потенциалов, создаваемых дипольным токовым источником в эллиптическом проводящем цилиндре конечной длины

Н. О. Стрелков, М. Н. Крамм

Национальный исследовательский университет «МЭИ»

Получена 9 ноября 2012 г.

Аннотация. Целью данной работы является реализация аналитического метода расчета электрических потенциалов, возбуждаемых токовым диполем в эллиптическом проводящем цилиндре конечной длины. Необходимость в таком методе связана с расчетом потенциалов на поверхности грудной клетки в прямых задачах электрокардиографии в квазистатическом приближении. В работе рассматривается аналитический способ расчета электрических потенциалов, основанный на разложении потенциала в двойные ряды по угловым и радиальным вариациям с использованием аппарата функций Матье. Предложены методики расчета и нормировки функций Матье. Рассматривается вопрос о выборе числа членов при суммировании двойных рядов. Проводится проверка предложенных формул путем сопоставления с результатами, полученными численными методами и другими авторами. Сравниваются распределения поверхностных потенциалов для кругового цилиндра (ряды с функциями Бесселя) и эллиптического цилиндра с малым эксцентриситетом.

Ключевые слова: распределение потенциала, проводящее тело, дипольный токовый источник, прямая задача, эллиптический цилиндр, периодические и модифицированные функции Матье.

Abstract. The aim of this work is the realization of the analytical method of calculation of electrical potentials, produced by the current dipole in elliptical conducting cylinder of finite length. The need for such a method is associated with the calculation of the potentials on the surface of the chest in the direct problems of cardiology in the quasi-static approximation. The work deals with the analytical method for calculation of electric potential, based on the expansion of potential in double series with respect to the angular and radial variations by using the Mathieu functions. Method of calculation and normalization of Mathieu functions is proposed. The question of choosing the number of the members of the summation of double series is considered. The proposed formulas checked by comparison with the results obtained by numerical methods and other authors. The distributions of surface potentials for a circular cylinder (series with Bessel functions) and for elliptic cylinder with a small eccentricity are compared.

Keywords: distribution of the potential, conducting body, the dipole current source, the direct problem, elliptical cylinder, periodic and modified Mathieu functions.

1. Введение

Расчет и анализ электрических потенциалов, возбуждаемых токовыми источниками в проводящих телах, представляют интерес в ряде практических задач, например в электрогеоразведке, электрокардиографии, электроэнцефалографии и других. Использование методики расчета электрических потенциалов актуально при решении обратных задач, связанных с неинвазивным определением (реконструкцией) координат и ориентации токовых источников по электрическим потенциалам, измеренным на поверхности проводящих тел. Известны численные методы решения уравнений теории поля (уравнения Пуассона и Лапласа) − это метод конечных элементов и метод граничных элементов (МКЭ и МГЭ, соответственно). Однако, при достаточно сложной форме поверхности проводящих тел и при учете внутренних неоднородностей в проводящих телах, вычислительная трудоемкость МКЭ и МГЭ становится препятствием на пути решения обратных задач, в которых прямой расчет потенциалов проводится многократно. В силу вышесказанного актуальным является анализ моделей проводящих тел, которые, с одной стороны отражают наиболее существенные свойства таких тел, и, с другой стороны, допускают аналитические методы расчета электрических потенциалов.

В работах [1-4] рассмотрены методы расчета потенциалов для случая аппроксимации поверхности проводящего тела сферой [1, 2] или сфероидом вращения [3, 4]. Однако, применительно, например, к задачам электрокардиографии более реалистичной является аппроксимация поверхности торса цилиндром конечной длины. Имеется несколько работ, посвященных расчетам потенциалов, возбуждаемых точечным токовым диполем в проводящем круговом цилиндре [5-13], в работе [14] рассмотрен случай эллиптического цилиндра.

Целью настоящей статьи является вычислительная реализация подхода, предложенного в работе [14], проверка сходимости используемых рядов функций Матье, сопоставление получаемых распределений поверхностных потенциалов с распределениями, полученными численными методами при различных ориентациях дипольного источника внутри эллиптического цилиндра конечной длины. Необходимо также убедиться в согласованности методов расчета потенциалов в круговом цилиндре и в эллиптическом цилиндре с малым эксцентриситетом.

2. Исходная задача

Рассматривается проводящий прямой эллиптический цилиндр высотой и полуосями эллипса соответственно большой и малой − и (рис. 1). Проводимость внутренней среды известна и равна . Пусть и − радиус-векторы точки наблюдения и точки источника, соответственно.

Рис. 1. Проводящий эллиптический цилиндр конечной длины.

Уравнение Пуассона для потенциала в данном случае имеет вид:

(1)

где − вектор дипольного момента точечного токового диполя; дифференцирование в правой части поводится по координатам источника. Проводящий цилиндр окружен воздухом с нулевой проводимостью, поэтому на поверхности цилиндра потенциал удовлетворяет граничному условию электрической изоляции:

(2), (3)

где − радиус-вектор точек, принадлежащих боковой поверхности цилиндра.

Решение исходной задачи. Решение уравнения Пуассона (1) может быть получено с помощью функции Грина , удовлетворяющей граничным условиям (2), (3) и являющейся, по сути, полем монопольного точечного источника [15]:

(4)

Следуя [10], функцию Грина можно представить в виде

(5)

где собственные функции удовлетворяют граничным условиям (2), (3) и являются решениями уравнения Штурма-Лиувилля [16]

(6)

со спектром собственных значений , причем суммирование в (5) проводится по всем собственным значениям, кроме . Собственные функции должны образовывать базис, нормированный по объему цилиндра:

(7)

Поскольку граничное условие (2) должно выполняться на поверхности эллиптического цилиндра, то разделение переменных в (6) проводится в эллиптических координатах:

(8)

где − расстояние между фокусами эллиптических оснований цилиндра, угловая координата , радиальная эллиптическая координата на поверхности цилиндра , где .

Следуя работе [14], решение уравнения Штурма-Лиувилля (6) в координатах методом разделения переменных приводит к собственным функциям

(9)

где и являются соответственно периодическими (угловыми) и модифицированными (радиальными) функциями Матье, т.е. решениями уравнений:

	(10)
	(11)

для одинаковых значений и . При подстановке (9) в (6), учитывая граничное условие (3) на основаниях цилиндра, получается характеристическое уравнение

(12)

Характеристические значения и определяются граничным условием (2) для радиальных функций Матье и условием периодичности по углу для угловых функций Матье. Существенно, что частные случаи (отсутствие вариаций в поперечной плоскости ) и (отсутствие вариаций вдоль оси цилиндра) приводят к частным выражениям для коэффициентов в (9) в связи с условием нормировки (7).

В работе [14] для удобства определения коэффициентов предложено использовать дополнительное нормирующее условие на функции Матье:

(13)

При этом в [14] получены следующие выражения для потенциалов, создаваемых токовыми диполями трёх базовых ориентаций:

(14)

для -ориентированного диполя ();

(15)

для -ориентированного диполя ();

(16)

для -ориентированного диполя (). Здесь и ; 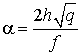, множитель в (4) принят для удобства за единицу. Формулы (14)-(16) записаны при , потенциал в случае получается в результате замен и на и , а также на . Здесь − площадь оснований цилиндров, а − множитель, используемый при преобразовании базисных векторов между декартовой и эллиптической системой координат.

В общем случае, когда присутствуют все компоненты вектора дипольного момента, потенциал определяется на основе формул (14)-(16) по принципу суперпозиции: .

3. Алгоритм вычисления потенциалов

Наибольший интерес для нас представляли вопросы реализации алгоритма вычислений потенциалов, так как эти вопросы в [14] практически не рассматриваются. Поскольку область проводящего цилиндра является односвязной, то в качестве функций Матье (ФМ) следует использовать угловые и модифицированные функции Матье первого рода: четные и нечетные угловые ФМ; четные и нечетные модифицированные (радиальные) ФМ [17, 18]. Существенно, что характеристические значения в (10)–(12) являются величинами, зависящими от параметра , и принимают различные значения для разных порядков ФМ, т.е. для четных функций при и для нечетных при (условие периодичности угловых ФМ). Значения параметра в свою очередь являются корнями производной радиальной ФМ порядка , удовлетворяющей граничному условию Неймана на боковой поверхности цилиндра (2): . Пусть и – корни четной и нечетной радиальных ФМ порядка с порядковым номером . С учётом этого суммы по и вида в выражениях для электрических потенциалов (14)–(16) можно заменить двойными рядами по порядкам функций и номерам корней производных радиальных функций – . При этом в рядах (14)–(16) следует выполнять суммирование отдельно по четным и по нечетным ФМ. Так, для случая имеем:

(17)

(18)

(19)

Преобразование данных формул к случаю обсуждалось выше. В полученных выражениях мы ввели коэффициенты и , которые необходимо определять из дополнительного условия нормировки (13):

(20)

где величины и находятся из выражений:

(21)

о коэффициентах и будет сказано ниже.

Расчет потенциала от диполя, обладающего всеми тремя проекциями вектора дипольного момента, выполняется по принципу суперпозиции на основе формул (17)–(19):

(22)

Использование приведенных выше формул позволяет выполнять расчет электрического потенциала, возбуждаемого произвольно расположенным диполем в проводящем эллиптическом цилиндре конечной длины. Однако такой расчет осложнен использованием функций Матье. В работе [14] авторы не останавливаются на этом вопросе, отмечая использование стандартных методов. Рассмотрим кратко представляющие практический интерес, использованные нами алгоритмы расчета функций Матье и особенности их программной реализации.

Расчет функций Матье. Для заданного порядка , параметра (и соответствующего характеристического значения ) и аргумента (угла или радиальной координаты ) значение соответствующей функции Матье вычисляется путём суммирования бесконечных рядов, содержащих произведения тригонометрических функций или (для периодических функций Матье) или обыкновенных функций Бесселя (для модифицированных функций Матье) и векторов коэффициентов Фурье и , . Коэффициенты Фурье также входят в выражения для расчета величин и в (21). Авторы работы [14] используют для нахождения этих коэффициентов метод цепных дробей [17, 18], который был предложен исторически первым и имеет множество программных реализаций [19–25]. Данный метод является численным, сложность вычисления корней получаемых трансцендентных уравнений растет с ростом порядка функций Матье, модуля параметра и номера коэффициента Фурье.

При использовании альтернативного метода эта проблема отсутствует. Он основан на построении бесконечной квадратной трёхдиагональной матрицы на основе рекуррентных выражений для коэффициентов Фурье [17, 26], впервые был предложен в [27], имеются программные реализации данного метода [21, 28-33].

Анализ большого числа программ для расчета функций Матье с использованием метода непрерывных дробей [23-25] и известных программ по методу трёхдиагональной матрицы [30-33], находящихся в свободном доступе, показал, что они оказываются непригодными для расчета рассматриваемой в настоящей работе задачи из-за ограничений на порядки функций и пределы изменения параметров и характеристических значений, входящих в функции Матье. Кроме этого, известные программы не рассчитывают производные ФМ в (18), (19) с должной точностью при значениях параметров рассматриваемой задачи.

Поэтому один из авторов настоящей работы (Н.О. Стрелков) совместно с профессором Roberto Coisson кафедры физики университета Пармы и его научной группой [34] разработал отдельную программную реализацию расчета функций Матье в бесплатном свободно распространяемом математическом пакете Scilab [35], получившую название Mathieu functions toolbox [36]. Она основана на построении трёхдиагональной матрицы для коэффициентов Фурье [32], была протестирована путём сравнения с таблицами и графиками, полученными другими авторами [18, 23, 37-41] для относительно малых порядков функций (до 20) и значений параметра (до 1600). Значения, полученные в ходе тестирования, практически совпали с рассчитанными ранее другими авторами [42]. Правильность работы построенной программы для других значений была проверена с помощью известных свойств ФМ и соотношений между этими функциями.

Особенности программной реализации расчета потенциалов. Исходными данными для расчета потенциалов являются: физические и геометрические параметры цилиндра - и ; параметры источника - ; координаты точки наблюдения ; число используемых порядков и корней производных радиальных функций .

Расчет начинается с вычисления радиальной координаты на боковой поверхности эллиптического цилиндра по формуле . Далее выполняется поиск корней производных модифицированных функций Матье первого рода первых порядков, удовлетворяющих граничному условию Неймана (2) - получаются соответственно значения и для четных и нечетных функций вместе со значениями коэффициентов Фурье. Такой поиск выполняется с помощью алгоритма Т. Деккера, представляющего собой комбинацию методов деления отрезка пополам, секущей и обратной квадратичной интерполяции [43]. При этом длина векторов коэффициентов и ограничена в соответствии с [23, 32].

Далее рассчитываются коэффициенты нормировки с использованием формул (20) и (21), причем вычисление интегралов выполняется численно по формуле трапеций [44].

Окончательно проводится суммирование потенциалов от отдельных проекций диполя (17)–(19) по методу суперпозиции (22) и вывод рассчитанного значения потенциала в заданной точке.

4. Обсуждение результатов

Проведем сравнение результатов расчетов, полученных в настоящей статье аналитически, по формулам (17)–(22) с результатами, полученными методом конечных элементов (МКЭ), и с результатами, представленными в работе [14]. Численное сравнение с МКЭ выполняется в точках равномерной сетки, построенной на боковой поверхности эллиптического цилиндра, с помощью следующих параметров: коэффициента корреляции (КК) и 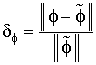– относительное отклонение (ОО), где – потенциалы, рассчитанные аналитически по формуле (22), – потенциалы, полученные с использованием МКЭ.

Как было отмечено авторами работы [14], в области, где вертикальные координаты диполя и точки наблюдения близки между собой (, причём ), наблюдается плохая сходимость двойных рядов. Поэтому потенциалы в таких точках нужно получать путем интерполяции. В настоящей работе используется алгоритм Дж. Эррико [45]. В табл. 1 представлены зависимости КК и ОО от величины , определяющей размер области плохой сходимости. При этом потенциалы рассчитываются в точках на боковой поверхности эллиптического цилиндра с параметрами м, м, м, См/м. Диполь расположен в центре оси цилиндра и имеет только вертикальную проекцию момента А∙м. Равномерная сетка на боковой поверхности цилиндра содержит 100 точек по периметру эллипса и 125 точек по высоте цилиндра, потенциалы в её точках рассчитываются с помощью МКЭ и по аналитическим формулам (17)–(22) при 20 порядках ФМ и 20 корнях производных радиальных ФМ.

Таблица 1. Зависимость КК и ОО от величины

≤ 0.005	0.01	0.015	0.02	≥ 0.025
0.99857	0.99967	0.99967	0.99991	0.99999
3.2	1.6	1.5	0.8	0.3

По данным табл. 1 можно сделать вывод, что использование значения уже в достаточной степени приближает друг к другу распределения, рассчитанные с помощью МКЭ и по аналитическим формулам. Поэтому далее в настоящей статье примем именно такое значение . Оно оказывается на 0.005 больше такового, полученного по результатам оценивания в [14], расширяя тем самым область интерполяции.

При выбранном значении было достигнуто совпадение формы рассчитанных распределений и представленных в [14], причем количественное отличие значений составило не более 1% по значениям экстремумов и характерным изолиниям.

Исследование влияния выбора числа членов разложений. Мы также провели анализ влияния выбора числа порядков ФМ и числа корней производных радиальных ФМ в суммах по и по ( и , соответственно) для двойных рядов в формулах (17)-(19). Рассматривался эллиптический цилиндр высотой м, длинами полуосей , м, проводимостью См/м. Пусть диполь расположен в точке с декартовыми координатами и обладает равными проекциями дипольного момента А∙м. Потенциалы рассчитывались в точках равномерной сетки размерности 100х125 точек. Определялся коэффициент корреляции и относительное отклонение распределений потенциалов на боковой поверхности цилиндра для различного количества порядков функций Матье и количества корней производных радиальных функций . Потенциалы в области рассчитывались путем интерполяции. Чтобы исключить влияние сдвига нуля при сравнении распределений потенциалов в каждом из методов расчета осуществлялась привязка нуля к точке с координатами , путем вычитания потенциала в этой точке. Результаты сравнения значений КК и ОО в зависимости от числа членов рядов представлены в табл. 2.

Таблица 2. Сравнение результатов численного и аналитического расчетов
для разного количества членов сумм для эллиптического цилиндра

N	M
	5		15		22
	r	, %	r	, %	r	, %
3	0.922538	34.94	0.913664	36.36	0.914335	36.23
10	0.980682	17.73	0.990824	11.71	0.990909	11.67
20	0.989712	12.98	0.999571	2.52	0.999594	2.46
30	0.990030	12.79	0.999960	0.77	0.999980	0.55
43	0.990041	12.78	0.999978	0.59	0.999997	0.20
50	0.990037	12.78	0.999978	0.58	0.999998	0.19

В соответствии с табл. 2 большие значения КК и малые значения ОО свидетельствуют о сходимости рядов (17)–(19) и об отсутствии заметных ошибок в алгоритме расчета потенциала, представленном в настоящей статье. Начиная с и , величины КК и ОО меняются слабо. По критерию максимума коэффициента корреляции при минимуме ОО оптимальными являются количества членов и . При последующем увеличении числа членов увеличивается только время расчета, ОО существенно не уменьшается, его величина практически определяется только шагом сетки в методе конечных элементов. Нормированные распределения потенциалов на боковой поверхности цилиндра, рассчитанные предложенным алгоритмом для различных значений и для вышеприведенных параметров задачи, представлены на рис. 2.

O	O
а) M = 5, N = 3	б) M ≥ 15, N ≥ 30
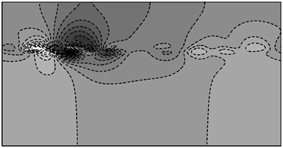
Рис. 2. Распределения потенциала на боковой поверхности эллиптического цилиндра для различных значений M и N

На рис. 2 по вертикальной оси отсчитывается координата вдоль образующей цилиндра, по горизонтальной - угол эллиптической системы координат, отсчитываемый от положительного направления оси в сторону положительного направления оси . Точке O соответствует точка с декартовыми координатами . По рисунку можно сделать вывод о схожести распределений потенциалов между собой, увеличение числа членов рядов приводит к уточнению формы распределения электрического потенциала.

Кроме представленных здесь распределений потенциалов были рассчитаны распределения для диполей, имеющих только одну проекцию вектора дипольного момента. При сравнении с распределениями, полученными с помощью МКЭ и использовании 50 порядков ФМ и 50 корней производных радиальных ФМ, среднее отличие коэффициента корреляции от единицы составило , а величина относительного отклонения – 0.2 %. Необходимо отметить, что в отличие от работы [14], мы пришли к выводу, что интерполяцию в области необходимо использовать для всех ориентаций вектора момента диполя, а не только для вертикальной.

Сопоставление моделей кругового и эллиптического цилиндров. Проводилось сравнение распределений потенциалов, создаваемых точечным токовым диполем на боковой поверхности кругового цилиндра и эллиптического цилиндра при варьировании эксцентриситета последнего.

Высота и проводимость обоих цилиндров составляли соответственно м, См/м. Радиус кругового цилиндра и длина большой полуоси эллипса основания эллиптического цилиндра (рис. 1) принимались равными м. Длина малой полуоси вычисляется через эксцентриситет эллипса по формуле . Диполь располагался в точке с координатами , проекции вектора дипольного момента были равны между собой .

Распределение потенциалов рассчитывались в точках равномерной по углу и высоте цилиндра сетки размерности 100х100 узлов по формулам из [11] для кругового цилиндра и по формулам (17)–(19) - для эллиптического. Распределения потенциалов сравнивались с помощью КК и ОО, зависимости этих параметров от эксцентриситета представлены на рис. 3.

Рис. 3. Зависимости коэффициента корреляции и относительной среднеквадратической погрешности потенциалов, рассчитанных на боковой поверхностях кругового и эллиптического цилиндра при варьировании эксцентриситета последнего. Число членов рядов M = N = 20.

Дополнительно на рис. 3 представлены в масштабе эллипсы со значениями отношения полуосей , соответствующие значениям эксцентриситета 0.01, 0.1,0.2,…,0.9, 0.99. Относительное отклонение распределений потенциалов и коэффициент корреляции достигается при (). Начиная с () отличия в распределениях потенциалов на боковой поверхности кругового и эллиптического цилиндров становятся заметными: , . Таким образом, распределение потенциалов для эллиптического цилиндра с соотношением полуосей вплоть до () практически не отличается от такового для кругового цилиндра. С точки зрения быстродействия для таких цилиндров целесообразно вести расчет по формулам кругового цилиндра, уменьшив тем самым временные затраты.

Однако, согласно [1, 14] для задач электрокардиографии отношение полуосей эллипса для торса человека лежит, в основном, в диапазоне (), для которого расчет потенциалов по модели кругового цилиндра дает заметные погрешности (см. рис. 3). Поэтому при решении задач электрокардиографии для астенически сложенных субъектов целесообразно использовать модель в форме эллиптического цилиндра с использованием соответствующих формул.

Таким образом, в настоящей статье был реализован аналитический метод расчета электрических потенциалов, создаваемых токовым диполем в эллиптическом проводящем цилиндре конечной длины. Представленные материалы наряду с работой [14] иллюстрируют одно из возможных применений функций Матье и дополняют эту работу в направлении разработки и апробации вычислительного алгоритма. Показана сходимость используемых рядов, а также сходимость решения при трансформации эллиптического цилиндра в круговой цилиндр. Авторы благодарят профессора Roberto Coisson кафедры физики университета Пармы за предоставленные материалы и советы.

Литература

1. Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. – М.: Наука. Физматлит, 1999. – 447 с.

2. Wilson F.N., Вауlеу R.Н. The electric field of an eccentric dipole in а homogeneous spherical conducting medium. // Circulation. 1950. V. 1. P. 84.

3. Yeh G.C.K., Martinek J. The potential of a general dipole in a homogeneous conducting prolate spheroid. // Ann. N. Y. Acad. Sci. 1957. V. 65. N. 6. P. 1003-1006.

4. Berry P.M. N, M space harmonics of the oblate spheroid // Ann. N. Y. Acad. Sci. 1957. V. 65. N. 6. P. 1126-1134.

5. Frank E. The Zero-Potential Contour on a Homogeneous Conducting Cylinder. IRE Trans. Med. Electron. 1, 27 (1953).

6. Burger H.C., Tolhoek H.A., Backbier F.G. The potential distribution on the body surface caused by a heart vector. // Amer. Heart. J. 1954. V. 48. N. 2. P. 249-263.

7. Okada R.H. Potential produced by an eccentric current dipole in a finite-length circular conducting cylinder // IRE Trans. Med. Electron. 1956. V. 7. P. 14.

8. Cornelis J.P.H., Nyssen E.H.G. Potentials Produced by Arbitrary Current Sources in an Infinite- and Finite-Length Circular Conducting Cylinder. // IEEE Trans. Biomed. Eng. 1985. V. BME-32. P. 993-1000.

9. Heringa A., Stegeman D.F. Comments on "Potentials produced by arbitrary current sources in an infinite- and finite-length circular conducting cylinder" // IEEE Trans. Biomed. Eng. 1987. V. BME-34. P. 73.

10. Mathews J., Walker R.L. Mathematical Methods of Physics. – Benjamin, New York, 1964, pp. 255-257.

11. Стрелков Н.О., Крамм М.Н., Винокуров Д.С. Методика расчета ЭКГ-карт наружных потенциалов для модели торса человека в виде кругового цилиндра // Сборник статей V Всероссийской научно-технической конференции "Информационные и управленческие технологии в медицине и экологии". - Пенза: Приволжский Дом знаний, 2011. – 164 с. С. 106-108.

12. Стрелков Н.О., Винокуров Д.С., Крамм М.Н.. Методика реконструкции параметров токового диполя сердца на модели торса человека в виде кругового цилиндра. // Медико-экологические информационные технологии – 2011: сборник материалов XIV Междунар. научн.-техн. конф. / редкол.: Н.А. Кореневский [и др.]; Юго-Зап. гос. ун-т. – Курск, 2011. – 315 с. С. 142-145.

13. Стрелков Н.О., Крамм М.Н., Жихарева Г.В.. Неоднородная электродинамическая модель грудной клетки человека в форме эллиптического цилиндра // Журнал радиоэлектроники. – 2011. – № 7. – [Электронный ресурс]. – URL http://jre.cplire.ru/jre/jul11/4/text.html (дата обращения 22 ноября 2012 г.).

14. Evrard R., Schmeits M., Troquet J. Calculation of the electrostatic-potential distribution in ohmic elliptical cylinders fed by a dipole source. // Journal of Applied Physics, vol. 91, no. 11, pp. 9393-9400, June 2002.

15. Barton G. Elements of Green’s Functions and Propagation. Clarendon, Oxford, 1989.

16. Lambin Ph., Troquet J. Complete calculation of the electric potential produced by a pair of current source and sink energizing a circular finite-length cylinder. // J. Appl. Phys. 1983. V. 54(7). P. 4174.

17. Мак-Лахлан Н.В. Теория и приложения функций Матье. Пер. с англ. – М.: Издательство иностранной литературы. 1953. – 475 с.

18. Абрамовиц М., Стиган И. Справочник по специальным функциям с формулами, графиками и математическими таблицами. - М.: Наука, 1979. 832 с.

19. Clemm D. Algorithm 352 Characteristic values and associated solutions of Mathieu’ differential equation. // Comm. of the ACM, 12(7), pp.399-408, July 1969.

20. Rengarajan S.R., Lewis J.E. Mathieu Funсtions of Integral Order and Real Arguments. // IEEE Trans. Microw. Theory and Tech., MTT-28(3), pp. 276-277, March 1980.

21. Shirts R.B. Algorithm 721 MTIEU1 and MTIEU2: Two subroutines to compute eigenvalues and solutions to Mathieu’ differential equation for noninteger and integer order. // ACM Trans. Math. Soft., 19(3), pp. 391-406, Sept. 1993.

22. Toyama N., Shogen K. Computation of the value of the even and odd mathieu funtions of order n for a given parameter s and an argument x. // IEEE Trans. Ant. and Propagat., AP-32(5), pp.537-539, May 1994.

23. Zhang S., Jin J. Computation of special functions. – John Wiley & Sons Inc., New York. 1996. – 717 p.

24. Mathieu Functions - GNU Scientific Library -- Reference Manual. – URL: http://www.gnu.org/software/gsl/manual/html_node/Mathieu-Functions.html. Дата обращения 22 ноября 2012 г.

25. Special functions (scipy.special) — SciPy v0.11 Reference Guide (DRAFT). – URL: http://docs.scipy.org/doc/scipy/reference/special.html. Дата обращения 22 ноября 2012 г.

26. Chaos-Cador L., Ley-Koo E. Mathieu functions revisited: matrix evaluation and generating functions. // Revista mexicana de física 48.1 (2002): p.67-75.

27. Früchting H. Fourier Coefficients of Mathieu Functions in Stable Regions. // J. of Research of Nac. Bureau of Standards, 73B(1), pp. 21-24, Jan. 1965.

28. Leeb W. Algorithm 537 Characteristic values of Mathieu’ differential equation. // ACM Trans. Math. Soft., 5(1), pp. 112-117, March, 1979.

29. Hodge D.B. The calculation of the eigenvalues and eigenvectors of mathieus equation. Nasa contractor report, The Ohio State University, Columbus, Ohio, 1972.

30. Mathieu Functions Toolbox v.1.0 - File Exchange - MATLAB Central. – URL: http://www.mathworks.com/matlabcentral/fileexchange/22081-mathieu-functions-toolbox-v-1-0. Дата обращения 22 ноября 2012 г.

31. Vibration Modes of an Elliptic Membrane - File Exchange - MATLAB Central. – URL: http://www.mathworks.com/matlabcentral/fileexchange/6500-vibration-modes-of-an-elliptic-membrane. Дата обращения 22 ноября 2012 г.

32. General Mathieu functions with arbitrary parameters V1.0 - File Exchange - MATLAB Central. – URL: