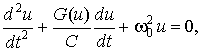УДК 621.373, 519.622

ОЦЕНКА ТОЧНОСТИ ЧИСЛЕННОГО АНАЛИЗА РЕЛАКСАЦИОННОГО ГЕНЕРАТОРА

 

А. М. Пилипенко, В. Н. Бирюков

Южный федеральный университет

Статья получена 6 ноября 2013 г.

 

Аннотация. В работе проведено тестирование современных численных методов решения обыкновенных дифференциальных уравнений. Рассмотренные методы широко применяются в программах схемотехнического и математического моделирования радиотехнических цепей и устройств. В качестве тестовой задачи выбрано дифференциальное уравнение релаксационного генератора. Впервые получены оценки точности численного моделирования релаксационного генератора во временной области. Показано, что на ошибку решения, кроме методической ошибки, существенное влияние оказывают случайные ошибки, вызванные синхронизацией ошибки численного решения с периодом колебания, с одной стороны, и изменением текущего шага решения, с другой.

Ключевые слова: численные методы, обыкновенные дифференциальные уравнения, релаксационный генератор, погрешность решения.

Abstract. In the paper the modern numerical methods for solving ordinary differential equations are testing. These methods are widely applied in simulators of RF circuits. As a test problem the relaxation oscillator’s differential equation with arbitrary polygonal nonlinearity was selected. An estimation of accuracy of numerical methods is received in the case of simulation of the relaxation oscillator. It is shown that the error of solution is determined by the methodological error and random errors caused by 1) an error of synchronization of the numerical solutions with the period of oscillation, 2) changes in the current step.

Keywords: numerical methods, nonlinear differential equations, relaxation oscillator, error analysis.

 

Введение

Компьютерное моделирование радиотехнических цепей и устройств во временной области заключается в численном решении систем обыкновенных дифференциальных уравнений (СОДУ). В современных пакетах схемотехнического проектирования и автоматизации инженерных расчетов реализовано большое количество численных методов решения СОДУ. Основными критериями эффективности численных методов являются их вычислительная сложность и точность получаемых решений. Точность компьютерного модели­рования количественно характеризует степень отклонения результатов моделирования от истинных результатов. Для теоретической оценки точности численных методов решения СОДУ используют тестовые, как правило, линейные СОДУ, для которых известно точное решение. Реальные радиотехнические устройства описываются нелинейными СОДУ, поэтому оценка точности их численного анализа представляет собой достаточно сложную задачу.

В работе [1] было проведено исследование точности современных численных методов при анализе автогенераторов гармонических колебаний. Данная статья является продолжением работы [1] применительно к другому классу автоколебательных цепей – генераторам релаксационных колебаний. Целью настоящей работы является оценка точности современных численных методов решения СОДУ при моделировании релаксационных генераторов.

Выбор задачи анализа генератора релаксационных колебаний в качестве тестовой обусловлен следующими причинами. Во-первых, релаксационный генератор является неотъемлемой частью многих радиоэлектронных устройств, таких как функциональные генераторы, радиоизмерительные приборы, счетчики, таймеры, устройства, инициирующие измерения или технологические процессы [2]. Во-вторых, задача численного анализа релаксационного генератора во временной области является одной из наиболее сложных для компьютерного моделирования, поскольку СОДУ, описывающая автогенератор, часто оказывается одновременно колебательной и жесткой [3]. Таким образом, оценка точности численного анализа релаксационного генератора необходима для выбора наиболее эффективного метода моделирования автоколебательных систем с различной степенью жесткости.

 

1. Модель релаксационного генератора

Релаксационные колебания возникают в нелинейных электрических цепях, не обладающих частотной избирательностью. Наиболее простая схемная модель релаксационного генератора может быть представлена также как и модель генератора гармонических колебаний – в виде параллельного соединения трех элементов – линейных емкости C и индуктивности L и нелинейного резистивного элемента, дифференциальное сопротивление (проводимость) которого может изменять знак [1].

Математическая модель релаксационного генератора (уравнение автогенератора) имеет вид нелинейного дифференциального уравнения второго порядка:

                                   (1)

где u – напряжение на выходе генератора, – резонансная частота LC-контура,  – дифференциальная проводимость нелинейного элемента, i(u) – вольт-амперная характеристика (ВАХ) нелинейного элемента.

Если дифференциальная проводимость G(u) на начальном участке ВАХ вблизи нуля принимает отрицательное значение, то в LC-контуре возникают автоколебания. При аппроксимации ВАХ нелинейного элемента полиномом третьей степени i(u) = a₁ u + a₃ u³ (a₁ < 0, a₃ > 0) уравнение (1) называется уравнением Ван-дер-Поля и для установившегося режима известны его аналитические решения. К сожалению, решение в явном виде получить не удается, и существуют только эталонные численные решения, специально вычисленные с высокой точностью для некоторых параметров уравнения и начальных данных [4].

Для получения аналитического решения уравнения автогенератора в установившемся режиме можно использовать методику, предложенную в работе [5]. Эта методика заключается в применении кусочно-линейной аппроксимации ВАХ нелинейного элемента. Такой подход позволяет определить стационарное решение уравнения автогенератора с точностью до последнего знака разрядной сетки компьютера.

Для релаксационного генератора характерны значительные потери, которые можно оценить затуханием , где  - характеристическая проводимость LC-контура, G₁ – дифференциальная проводимость нелинейного элемента при di / du > 0. В случае значительных потерь d > 2 и решение линейного однородного дифференциального уравнения второго порядка описывается суммой двух экспоненциальных функций. Таким образом, при использовании симметричной кусочно-линейной функции для аппроксимации ВАХ нелинейного элемента аналитическое выражение для напряжения на выходе релаксационного генератора в установившемся режиме имеет вид [1]

                               (2)

где A₁, A₂, A₃, A₄ – постоянные интегрирования; t₀ – момент времени, в который проводимость нелинейного элемента меняет знак; T – период колебаний;  и  - постоянные времени автогенератора при G(u) = G₀ < 0 и G(u) = G₁ > 0 соответственно; .

На рис. 1 показаны точные стационарные решения уравнения автогенератора, полученные с помощью выражения (2) при двух различных значениях затухания d = 4 (сплошная линия) и d = 100 (штриховая линия), значения остальных параметров автогенератора были заданы следующим образом: L = 1 Гн, С = 1 Ф, G₀ = - 4 См.

 

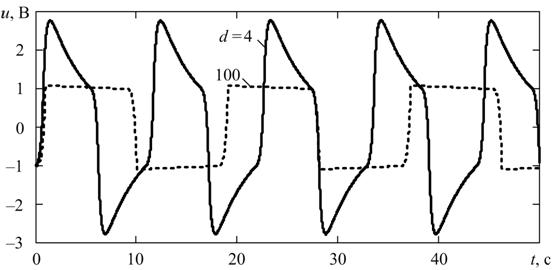
Рис. 1. Точные стационарные решения уравнения автогенератора.

 

Следует отметить, что при d = 4 модель автогенератора (1) может считаться слабо жесткой, так как в этом случае коэффициент жесткости, равный отношению максимальной и минимальной постоянных времени автогенератора η = τ_max / τ_min ≈ 10 > 1. При d = 100 модель (1) является жесткой, так как в этом случае η ≈ 10⁴ >> 1.

Полученные аналитические решения позволяют с точностью до последнего знака разрядной сетки компьютера оценить основные параметры колебаний на выходе автогенератора. В таблице 1 приведены точные максимальные значения A_m0 и точные значения частот f_m0 релаксационных колебаний, представленных на рис. 1.

 

Таблица 1.

d	η	Am0, В	fm0, Гц
4	10	2.765625375929214	0.09132317033942401
100	10 4	1.084334602144661	0.05506258511132066

 

2. Численное решение уравнения автогенератора

В данной работе проведена оценка точности моделирования релаксационного генератора во временной области при использовании трех численных методов решения СОДУ: метода трапеций (TR), Гира (BDF) и RADAU5. Подробное описание указанных методов приведено в работах [6, 7]. Выбор для численного анализа методов TR и BDF объясняется тем, что они являются основными методами для анализа переходных процессов в программах схемотехнического моделирования. Метод RADAU5 является одним из наиболее перспективных методов типа Рунге-Кутты для решения жестких задач [7]. Следует отметить, что метод RADAU5 является трехста­дийным, поэтому его применение сводится к решению системы алгебраических уравнений, порядок которой в три раза больше порядка СОДУ заданной цепи. Методы TR и BDF – одностадийные, таким образом, вычислительная сложность этих методов, определяющая затраты машинного времени и оперативной памяти на получение решения, минимальна. Многостадийные методы обладают повышенной L-устойчивостью и рекомендуются для решения задач высокой жесткости [8, 9].

Для оценки точности перечисленных выше численных методов применим методику, предложенную в работе [10] и основанную на анализе точности оценки основных параметров генерируемого колебания – частоты и амплитуды (максимального значения). Текущие относительные погрешности оценки частоты и амплитуды соответственно определяются с помощью следующих соотношени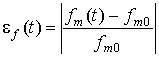й

 и ,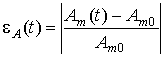

 

где f_m(t) и A_m(t) – оценки частоты и амплитуды генерируемого колебания, полученные из решения уравнения (1) численными методами.

На рис. 2 и рис. 3 приведены временные диаграммы относительных погрешностей оценки частоты и амплитуды стационарного колебания релаксационного генератора при различном затухании и соответственно жесткости колебательной системы (см. таблицу 1). Решение системы уравнений (1) осуществлялось перечисленными выше численными методами при заданном максимальном шаге h_max = T / 1000 и предельно допустимой относительной погрешности TOL = 10 ^- 5. Для оценки частоты колебаний использовалась линейная интерполяция численного решения в точках изменения знака u(t), для оценки амплитуды – квадратичная в точках локальных экстремумов. Интервал наблюдения выбран соответствующим стационарному режиму генерации.

Из рис. 2 и рис. 3 следует, что параметры процесса f_m(t) и A_m(t) изменяются от периода к периоду существенно. Для количественного описания полученных результатов в таблице 2 приведены средние значения относительных погрешностей оценки частоты и амплитуды колебаний (m_εω и m_εA соответственно) и среднеквадратические отклонения (СКО) относительных погрешностей оценки частоты и амплитуды колебаний (σ_εω и σ_εA соответственно).

 

      

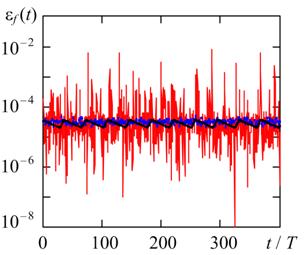
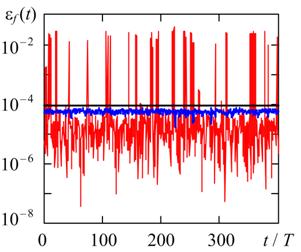
(а)                             ,                              (б)

Рис. 2. Текущие относительные погрешности оценки частоты релаксационного колебания методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 1000, TOL = 10 ^- 5 и различной жесткости модели автогенератора η = 10 (а) и η = 10 ⁴ (б).

 

       

(а)                                                            (б)

Рис. 3. Текущие относительные погрешности оценки амплитуды релаксационного колебания методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 1000, TOL = 10 ^- 5 и различной жесткости модели автогенератора η = 10 (а) и η = 10 ⁴ (б).

 

Таблица 2.

η	10			10 4
Метод	TR	BDF	RADAU5	TR	BDF	RADAU5
mεω	2.7∙10-5	3.1∙10-5	1.2∙10-4	8.7∙10-5	5.5∙10-5	1.7∙10-3
σεω	4.8∙10-6	4.5∙10-6	5.1∙10-4	1.7∙10-6	7.2∙10-6	5.8∙10-3
mεA	5.6∙10-6	1.4∙10-5	4.7∙10-5	4.0∙10-4	2.6∙10-5	2.2∙10-4
σεA	3.7∙10-6	4.2∙10-6	2.1∙10-4	1.3∙10-4	1.9∙10-5	2.3∙10-3

 

Приведенные на рис. 2, рис. 3 и в таблице 2 результаты численного анализа показывают, что метод RADAU5, как правило, имеет наибольшие значения относительных погрешностей как при оценке частоты, так и при оценке амплитуды релаксационных колебаний независимо от жесткости задачи. Кроме того, текущие значения погрешностей для метода RADAU5 могут на один-два порядка превышать аналогичные погрешности методов BDF и TR. Особенно ярко этот эффект проявляется при оценке частоты в случае высокой жесткости задачи (см. рис. 2, б). В случае слабой жесткости системы (1) (η = 10) относительные погрешности для методов BDF и TR имеют одинаковый порядок величины. При высокой жесткости (η = 10 ⁴) текущие погрешности ε_f (t) и ε_A(t) оказываются наименьшими для метода BDF, причем среднее значение погрешности оценки амплитуды для метода BDF меньше аналогичного значения для метода TR примерно в 15 раз. Следует также отметить, что погрешности метода BDF наиболее слабо зависят от жесткости задачи по сравнению с погрешностями других рассмотренных методов. Как видно из таблицы 2 при увеличении жесткости задачи в 1000 раз относительные погрешности для метода BDF возрастают не более чем в 4.5 раза, а для методов TR и RADAU5 могут увеличиваться более чем в 50 раз.

Из рис. 2 и рис. 3 следует, что для методов TR и BDF может наблюдаться эффект «синхронизации» ошибки с периодом генерируемых колебаний. При этом текущие погрешности имеют, как правило, периодический характер, причем период изменения погрешностей кратен периоду генерируемых колебаний. Кроме «ошибки синхронизации» второй случайной составляющей является ошибка, наблюдаемая в методах BDF и RADAU5, вызванная алгоритмом изменения шага в процессе решения.

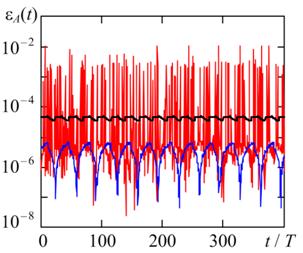
Для проверки корректности реализованной методики оценки точности на рис. 4 и рис. 5 приведены текущие относительные погрешности оценки частоты и амплитуды релаксационного колебания методами TR, BDF и RADAU5 при уменьшении h_max в 2 раза и TOL в 4 раза по сравнению со случаем представленным на рис. 2 и рис. 3.

Из сравнительного анализа погрешностей, приведенных на рис. 2, 3 и на рис. 4, 5 видно, что при уменьшении TOL в 4 раза средние значения и СКО погрешностей методов TR и BDF также уменьшаются примерно в 4 раза, а эффект синхронизации ослабевает. Для метода RADAU5 уменьшение погрешностей происходит только в случае слабо жесткой задачи, а в случае жесткой задачи наблюдается значительный рост текущих погрешностей ε_f (t) и ε_A(t). Такой эффект для метода RADAU5 можно объяснить резким ростом погрешности округления при уменьшении шага решения. Погрешность округления метода RADAU5 возрастает из-за плохой обусловленности соответствующей ему системы алгебраических уравнений, порядок которой в три раза больше порядка исходной СОДУ [7].

 

      

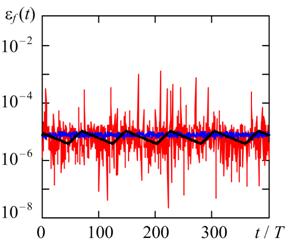
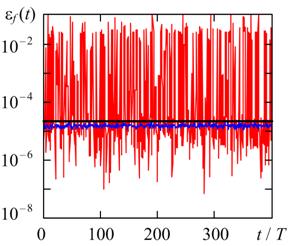
(а)                                                          (б)

Рис. 4. Текущие относительные погрешности оценки частоты релаксационного колебания методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 2000, TOL = 0.25∙10 ^- 5 и различной жесткости модели автогенератора η = 10 (а) и η = 10 ⁴ (б).

 

   

(а)                                                          (б)

Рис. 5. Текущие относительные погрешности оценки амплитуды релаксационного колебания методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 2000, TOL = 0.25∙10 ^- 5 и различной жесткости модели автогенератора η = 10 (а) и η = 10 ⁴ (б).

 

3. Оценка случайной составляющей погрешности численного анализа при отсутствии точного решения

Следует отметить, что анализ погрешности численного решения можно провести частично и в том случае, когда точное решение отсутствует. Точность можно оценить, рассчитав относительные отклонения значений параметров колебания, полученных в различные моменты времени (здесь на текущем и последующем периоде решения):

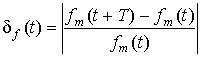 и .

В общем случае приращения погрешностей на смежных периодах должны быть меньше опционной погрешности. Однако, как показано на рис. 6 и рис. 7, зависимости δ_f (t) и δ_A(t), полученные при решении уравнения (1) теми же методами и при таких же значениях h_max и TOL, что зависимости ε_f (t) и ε_A(t) на рис. 4, б и рис. 5, б, не всегда малы. Таким образом, избыточный шум решения может быть обнаружен и без определения точных значений параметров процесса.

 

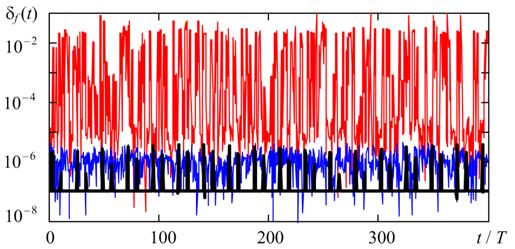
Рис. 6. Зависимости δ_f (t), полученные методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 2000, TOL = 0.25∙10 ^- 5 и η = 10 ⁴.

 

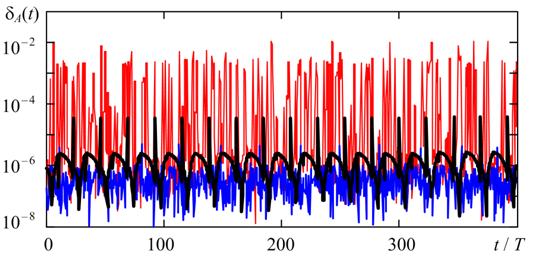
Рис. 7. Зависимости δ_A(t), полученные методами TR (черная кривая), BDF (синяя кривая) и RADAU5 (красная кривая) при h_max = T / 2000, TOL = 0.25∙10 ^- 5 и η = 10 ⁴.

 

4. Обсуждение результатов

Оценка точности решения конкретной задачи по локальной или даже интервальной (глобальной) погрешности не дает общего представления о точности анализа моделируемого численно процесса. Зачастую для доказательства пригодности (или непригодности) метода приводится график решения одномерной или двумерной задачи [7, 9]. Отсутствие количественной оценки качества моделирования исследуемого процесса приводит к попыткам дополнения понятия «погрешность решения» понятием «достоверность решения». В настоящей работе (и в работе [1]) оценка погрешности решения проведена по параметрам исследуемого периодического процесса. Такой подход позволяет заменить огромный массив данных текущих погрешностей намного более компактным и обозримым, что позволяет в ряде случаев произвести более подробный анализ структуры погрешности, недоступный графическим методам. В рассмотренном случае у метода RADAU5 выявлена существенная составляющая погрешности, вызванная, по-видимому, несовершенством алгоритма автоматического выбора шага. Соответствующий алгоритм Гира оказался, напротив, весьма эффективным. Оценка погрешности решения по параметрам стационарного процесса позволяет обнаружить случайные составляющие погрешности, связанные с синхронизацией решения с шагом и несовершенством алгоритма выбора шага, для любой задачи с периодическим решением без определения точного решения.

 

Заключение

Проведенная оценка точности численного анализа релаксационного генератора дополняет известные теоретические и экспериментальные оценки свойств численных методов решения дифференциальных уравнений для осциллирующих систем, приведенные в работах [1, 10, 11]. Контроль точности методов осуществлялся не по погрешности определения переменной, а по погрешностям определения основных параметров стационарного процесса – частоты и размаха колебания. В качестве тестовой рассмотрена задача анализа автогенератора, в котором ВАХ нелинейного элемента аппроксимируется кусочно-линейной функцией, что позволяет получить точное стационарное решение и его основные параметры, необходимые для оценки погрешностей тестируемых численных методов.

Результаты тестирования численных методов, полученные в данной работе, позволяют обосновать выбор того или иного метода для получения достоверных и наиболее точных результатов моделирования автоколебательных систем с различной степенью жесткости. Кроме того, в данной работе предложен и обоснован метод оценки точности численного анализа нелинейных колебательных систем при отсутствии точного решения.

 

Работа выполнена при поддержке стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования по приоритетным направлениям модернизации российской экономики (СП-398.2012.5).

 

Литература

1.     Пилипенко А. М., Бирюков В. Н. Исследование эффективности современных численных методов при анализе автоколебательных цепей // Журнал радиоэлектроники: электронный журнал, 2013, № 8, URL: http://jre.cplire.ru/jre/aug13/9/text.html.

2.     Хоровиц П., Хилл У. Искусство схемотехники / пер. с англ. 7-е изд. М.: Мир. БИНОМ, 2010, 704 с.

3.     Пилипенко А. М., Бирюков В. Н. Гибридные методы решения обыкновенных дифференциальных уравнений жестких и/или колебательных цепей // Радиотехника, 2011, № 1, с. 11–15.

4.     Гужев Д. С., Калиткин Н. Н. Уравнение Бюргерса – тест для численных методов // Математическое моделирование, 1995, Т.7, №4, с. 99 – 127.

5.     Бирюков В.Н., Гатько Л.Е. Точное стационарное решение уравнения автогенератора // Нелинейный мир, 2012, Т. 10, № 9, с. 613-616.

6.     Хайрер Э., Нёрсетт С., Ваннер Р. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990, 512 с.

7.     Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999, 685 с.

8.     Калиткин Н. Н. Численные методы решения жестких систем // Математическое моделирование, 1995, Т.7, №5, c. 8 – 11.

9.     Maffezzoni P., Codecasa L., D’Amore D. Time-domain simulation of nonlinear circuits through implicit Runge-Kutta methods // IEEE Transactions. Circuits and Systems, 2007, v. 54, n. 2, pp. 391 – 400.

10.  Бирюков В. Н., Пилипенко А. М. Ковтун Д.Г. Оценка точности численного анализа генератора гармонических колебаний во временной области // Радиотехника, 2011, № 9, с. 104-107.

11.   Biryukov V. N., Pilipenko A. M. An Approach to Estimate the Error of Oscillator Time-Domain Analysis // Proceedings of IEEE East-West Design and Test Symposium (EWDTS'2013), 2013, pp. 223-226.