КОРОТКИЕ ВОЛНОВОДНЫЕ ТРАНСФОРМАТОРЫ СОПРОТИВЛЕНИЙ

Б. В. Прокофьев, М. А. Мартыненко

ФГУП «НПП «Торий», Москва

Статья получена 6 ноября 2013 г.

Аннотация.  Описаны возможные конструкции широкополосных волноводных трансформаторов сопротивлений, длина которых в несколько раз меньше длины классических четвертьволновых трансформаторов. Исследования выполнены с помощью вычислительного эксперимента с использованием программы Н-WINDOW.

Ключевые слова: волноводный трансформатор сопротивлений, широкая полоса, короткая длина, вычислительный эксперимент.

Abstract. Possible structures of the broadband waveguide impedance transformers are described, whose length can be several times less as that of the classic quarter-wave transformers. The investigations have been carried out by means of the computational experiment based on the H-WINDOW code.

Key words: waveguide impedance transformer, broad band, short length, computational experiment.

 

1. Введение

Для согласования волноводных трактов с отличающимися размерами поперечных сечений используют волноводные трансформаторы сопротивлений. Эффект согласования в заданной полосе частот по понятным причинам стремятся получить наиболее экономными методами. По этой причине одной из самых распространенных конструкций стал пирамидальный (в частном случае, клиновидный) волноводный переход, который применяют при небольших перепадах волновых сопротивлений. Однако качество согласования такого перехода сильно зависит от его длины (рис. 1). При перепадах волновых сопротивлений  подобные переходы имеют большую длину и их использование, особенно, в длинноволновой части СВЧ диапазона, оказывается нежелательным в связи с чрезмерной массой и габаритами. Значительно меньшую длину при высоком качестве согласования имеют ступенчатые трансформаторы сопротивлений. Классические волноводные трансформаторы сопротивлений в виде последовательности четвертьволновых ступенек хорошо изучены и подробно описаны в научно-технической и справочной литературе [1,2]. Известны также небезуспешные попытки дальнейшего уменьшения длины волноводных трансформаторов, основанные на применении комбинации ступенек и диафрагм в прямоугольном

волноводе [3,4]. Целью настоящей работы было исследование возможностей дальнейшего уменьшения продольных размеров и расширения полосы пропускания волноводных трансформаторов сопротивлений. Описываемые ниже исследования проводились на основе вычислительного эксперимента с применением программы H-WINDOW, алгоритм которой описан в работе [5].

 

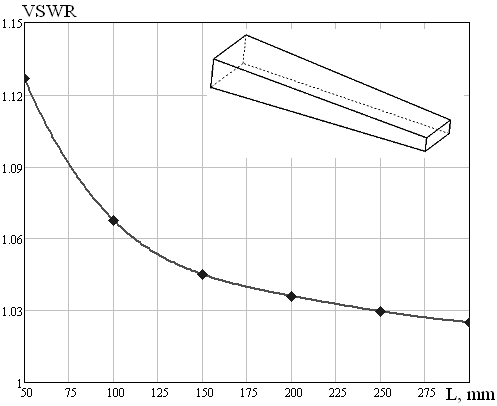
Рис. 1. Зависимость КСВН от длины L пирамидального перехода с волновода сечением   мм² на волновод сечением  мм².

 

2. Результаты вычислительного эксперимента

При оптимизации волноводных трансформаторов сопротивлений с помощью метода симплексов Нелдера-Мида [6] использовалась одна из двух функций цели, первая из которых позволяет получить характеристику согласования, близкую к максимально плоской:

,

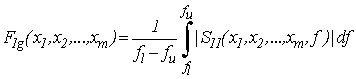а вторая – характеристику чебышевского типа:

.

В приведенных формулах  – подлежащие определению размеры трансформатора сопротивлений;  – нижняя и верхняя частоты заданной полосы пропускания;  – частота, на которой коэффициент отражения  принимает максимальное значение (определяется автоматически в процессе вычислений).

Простейшим трансформатором сопротивлений является, как известно, одноступенчатый переход [7]. Длина ступеньки в нем примерно равна четверти волноводной длины волны, а поперечные размеры ступеньки выбирают такими, чтобы ее волновое сопротивление  удовлетворяло условию:

где – волновые сопротивления передающих линий слева и справа от ступеньки. В частности, для волноводов одинаковой ширины  с разными размерами узких стенок  (переход в Е-плоскости) ширина ступеньки выбирается равной ширине волноводов, а высоту ступеньки  выбирают равной величине

Полоса пропускания одноступенчатого перехода зависит от соотношения величин . Согласование, близкое к идеальному, получается только на одной частоте, вне которой коэффициент отражения монотонно возрастает. Переходы с такой характеристикой согласования используют для передачи мощности СВЧ на фиксированной частоте или в узкой полосе частот, обычно не превышающей нескольких процентов. Полосу пропускания перехода в Е-плоскости с одной согласующей ступенькой можно увеличить, превратив этот переход в неоднородный и сделав ширину ступеньки большей ширины входного и выходного волноводов [2].  При этом существует ширина ступеньки, для которой полоса пропускания получается максимальной. Достигаемый эффект увеличения полосы пропускания объясняется уменьшением дисперсии волны в волноводной ступеньке, а существование оптимальной ширины ступеньки – тем, что дальнейшее увеличение ширины приводит к росту отражений на стыках ступеньки с входным и выходным волноводами. Эффект уменьшения волноводной длины волны Н₁₀ в прямоугольных волноводах при увеличении их ширины может быть использован и для сокращения продольных размеров трансформаторов сопротивления.

Общепринятый способ расширения полосы пропускания трансформаторов сопротивлений состоит в наращивании числа ступенек, длина которых примерно равна четверти волноводной длины волны. Соответственно, волноводные трансформаторы сопротивлений порой определяют именно как последовательность четвертьволновых отрезков линии передачи, волновое сопротивление которых меняется по определенному закону [1]. Следствием подобного подхода к конструированию трансформаторов сопротивлений является неоправданно большая длина таких устройств из-за большого числа ступенек в тех случаях, когда требуется получить согласование в широкой полосе частот. Между тем размеры переходов можно значительно сократить, если использовать комбинацию ступенек и диафрагм. Так, характеристику согласования, подобную характеристике двухступенчатого трансформатора, можно получить, заменив одну из ступенек резонансной диафрагмой. На рис. 2 представлены зависимости коэффициента отражения от частоты для однородного двухступенчатого трансформатора сопротивлений (1) и трансформатора, состоящего из одной ступеньки с диафрагмой (2). При несколько худшем качестве согласования длина такого перехода оказывается заметно меньшей, чем у двухступенчатого перехода.

 

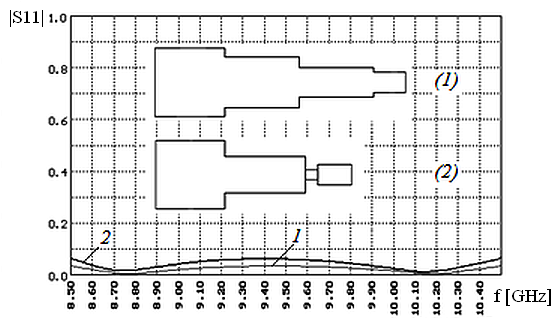
Рис. 2. Сравнительные размеры и зависимости коэффициента отражения  от частоты  двухступенчатого трансформатора сопротивлений (1) и одноступенчатого трансформатора с дополнительной диафрагмой (2).

 

Для расширения полосы пропускания к описанному выше трансформатору с диафрагмой можно добавить еще одну ступеньку. Оказалось, что если сделать такой трансформатор неоднородным, применив в нем ступеньки увеличенной ширины, то получается очень компактный переход, длина которого оказывается в 3-4 раза меньше, чем у классического четвертьволнового перехода с аналогичными характеристиками согласования. Так, неоднородный трансформатор, представленный на рис. 3, имеет длину всего около 27 мм при коэффициенте отражения  в полосе частот около 50%. Переход характеризуется следующими размерами сту­пенек:  мм³  (первая ступенька);     мм³  (вторая ступенька);  мм³ (диафрагма). Выходной и входной волноводы имеют сечения, соответст­венно равные  мм²  и  мм².

 

Рис. 3. Двухступенчатый волноводный трансформатор сопротивлений с  дополнительной резонансной диафрагмой.

 

Отметим, что классический четвертьволновый трансформатор с близкой характеристикой коэффициента отражения должен иметь шесть ступенек при общей длине около 109 мм. Ступеньки этого трансформатора имеют следующие размеры:  мм³;  мм³;  мм³;  мм³;  мм³:  мм³. Сравнение характеристик согласования трансформатора из двух ступенек с диафрагмой (кривая 1) и трансформатора на основе четвертьволновых ступенек (кривая 2) приведено на рис. 4.

Согласующая диафрагма не всегда должна находиться на стыке с выходным волноводом меньшего сечения. Так, для перехода с сечения  мм² на сечение  мм² оптимальным оказалось расположение диафрагмы на стыке двух ступенек:  мм³  (первая ступенька);  мм³  (диа­фрагма);  мм³; (вторая ступенька). Рассчитанный коэффициент отражения для такого

перехода имеет максимальное значе­ние  в полосе частот  ГГц. Общая длина перехода составляет всего 19,2 мм. Между тем коэффициент отражения пирамидального перехода длиной 40 мм с линейной зависимостью высоты волновода от продольной координаты в той же полосе частот оказывается в 3 раза большим.

 

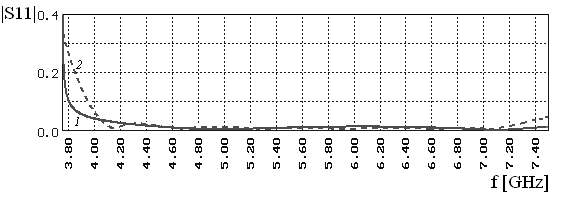Рис. 4. Зависимость коэффициента отражения от частоты для двухступенчатого трансформатора с диафрагмой  (1) и шестиступенчатого четвертьволнового трансформатора (2).

Рассмотрим еще один практически важный случай, когда размер широ­кой стенки входного волновода меньше размера широкой стенки выход­ного волновода, а размер узкой стенки входного волновода превышает размер узкой стенки выходного волновода. Используя описанный подход, при рассмотрении способов построения такого перехода оказывается возможным отказаться от громоздких решений, основанных на каскадном вклю­чении двух переходов с последовательным изменением сначала одного, а затем другого размера. Простая конструкция из двух ступенек с диафрагмой применима и к этому случаю (рис. 5). Например, оптимальные размеры перехода для входного волновода 48´24 мм² и выходного волновода 58´14 мм² составили:  мм³ (первая ступенька);   мм³  (вторая ступенька);  мм³  (диафрагма). Общая длина L перехода составляет всего 36,6 мм при ширине полосы пропускания около 40% по уровню коэффициента отражения  (рис. 6). Другие конструкции переходов, в том числе, решающие эту задачу путем увеличения на каждом стыке одного из поперечных размеров и уменьшения другого, оказываются более узкополосными и/или требуют использования большего числа ступенек. На рассмотренном примере можно убедиться и в том, что для изначально неоднородного трансформатора сопротивлений использование ступенек увеличенной ширины обеспечивает значительный выигрыш, как в длине перехода, так и в ширине его полосы пропускания.

 

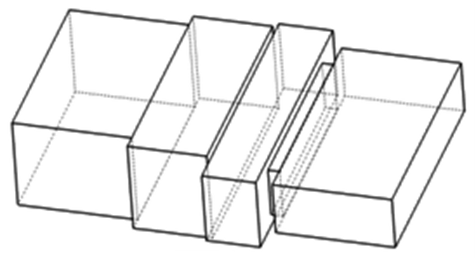
Рис. 5. Конфигурация трансформатора сопротивлений при разнонаправленном изменении размеров стенок входного и выходного волноводов.

 

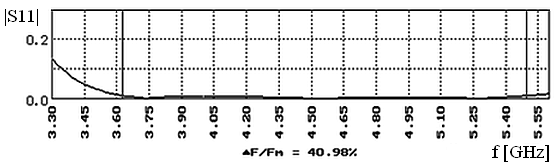
Рис. 6. Зависимость коэффициента отражения от частоты для трансформатора,  представленного на рис. 5

 

В приведенных выше примерах отношение сопротивлений согласуемых волноводов не превышает двух, хотя при необходимости получения согласования в более узкой полосе это отношение может быть увеличено. Так, проведенные расчеты показали, что при  для перехода, состоящего из двух ступенек и резонансной диафрагмы (рис. 3) можно получить полосу пропускания, равную 35% по уровню коэффициента отражения  Если требуется получить высокое качество согласования в широкой полосе частот при больших отношениях сопротивлений по обе стороны трансформатора, то описанные методики согласования можно усовершенствовать. В простейшем случае можно добавить еще одну диафрагму, установив ее между двумя ступеньками (рис. 7).  При размерах входного и выходного волноводов  мм² и  мм² , а также размерах ступенек и диафрагм  мм³;  мм³; мм³;  мм³ трансформатор имеет полосу пропускания  ГГц (35%) по уровню коэффициента отражения . 

 

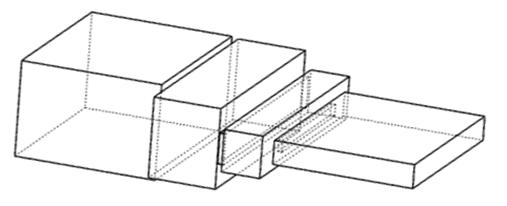
Рис. 7. Двухступенчатый волноводный трансформатор сопротивлений с двумя резонансными диафрагмами.

При необходимости получения более широкой полосы пропускания и/или большего перепада волновых сопротивлений можно включить дополнительные ступеньки, согласованные емкостными диафрагмами  в промежуток между первой и последней ступеньками в схеме перехода, представленной на рис. 3. В схеме такого трансформатора, показанной на рис. 8, выходной и входной волноводы также имеют размеры  мм и  мм. Ступеньки и диафрагмы имеют следующие размеры:  мм³;   мм³;   мм³;   мм³;  мм³;  мм³.  Общая длина трансформатора, таким образом, составляет 33,7 мм. При этом его коэффициент отражения  не превышает 0,01 в полосе частот  ГГц (45%). Эквивалентные по величине коэффициента отражения и полосе пропускания классические трансформаторы сопротивлений должны иметь не менее пяти четвертьволновых ступенек при общей длине около 76 мм.

 

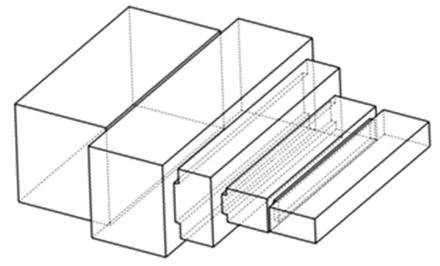
Рис. 8. Трехступенчатый волноводный трансформатор сопротивлений с одной резонансной и двумя емкостными диафрагмами.

 

3. Обсуждение результатов и выводы

Использованный в работе метод вычислительного («машинного») эксперимента позволил найти варианты волноводных трансформаторов сопротивлений, отличающиеся простотой конструкции, широкой полосой пропускания  и наименьшими продольными размерами по сравнению с ранее известными конструкциями волноводных трансформаторов. В частности, рассмотренные компактные трансформаторы оказались короче описанных в работе [4] однородных трансформаторов сопротивлений, состоящих из последовательности емкостных и индуктивных ступенек.

 Широкополосность рассмотренных трансформаторов является следствием резкого сокращения их продольных размеров путем принятия описанных мер, которые позволили уменьшить зависимость электрической длины составляющих переходы элементов (ступенек и диафрагм) от частоты. Следует также отметить, что ввиду малой длины и увеличенной ширины ступенек в ряде случаев возникает необходимость учета взаимодействия соседних волноводных стыков на высших типах волн, вследствие чего может потребоваться небольшая коррекция размеров отдельных ступенек и диафрагм. На практике такая коррекция может быть легко выполнена с помощью какой-либо из программ трехмерного расчета электродинамических систем. Авторами с этой целью использовалась также специально разработанная программа R-WINDOW, созданная на базе алгоритма программы Н-WINDOW и позволяющая учитывать взаимодействие близкорасположенных стыков в прямоугольных волноводах.

Некоторые из описанных конструкций волноводных трансформаторов сопротивлений в настоящее время успешно применяются в устройствах ввода-вывода энергии ряда широкополосных электровакуумных приборов СВЧ, а также в измерительных волноводных трактах.

 

Литература

1.       Фельдштейн, А. П., Явич Л. Р., Смирнов В. П.  Справочник по элементам волноводной техники // М.: Советское радио, 1967.

2.       Matthaei, G. L., Young, L., Jones E. M. T. Microwave filters, Impedance-Matching Networks and Coupling Structures // Dedham, MA: Artech House, 1980.

3.       Пат. 4041420 США, МКИ H01p 5/08, Кл. США 333/35 / Shunted Stepped Waveguide Transition / H. J. Riblet; заявлено 30.06.76 ; опубл. 09.08.77.

4.       Matthaei, G. L. Tables of Chebyshev Impedance-Transforming Networks of Low-Pass Filter Form  // Proc. of the IEEE.  Vol. 52. No. 8.  August 1964. P. 939-963.

5.       Прокофьев, Б. В. Расчёт матриц рассеяния баночных окон сложной конфигурации  для волноводных вводов (выводов) энергии ЭВП СВЧ // Электронная техника.  Сер.1. Электроника СВЧ. 1991. Вып. 3(437). С. 4-9.

6.       Банди, Б. Методы оптимизации // М.: Радио и связь. 1988.

7.       Пат. 2106769 США, Кл. США 178-44/  Transmission of guided waves/ G. C. Southworth; заявлено 23.08.35; опубл. 01.02.38.