УДК 621.396.67.012
Повышение быстродействия пространственной фильтрации помех в РЛС с АФАР
Р. П. Быстров 1, А. В. Новиков 2, В. Л. Румянцев 2
1 Институт радиотехники и электроники им. В.А. Котельникова РАН, г. Москва
2 ОАО ЦКБА, г. Тула
Статья получена 30
октября
2014 г.
Аннотация. Проведено рассмотрение задачи пространственной фильтрации помех в РЛС с АФАР. Определены основные критерии качества работы пространственного фильтра и методы непосредственного вычисления оптимального весового вектора. Предложен вариант повышения быстродействия системы помехозащиты на базе АФАР за счет доработки алгоритма решетчатой фильтрации, учитывающего свойство персимметрии выборочной корреляционной матрицы помеховых сигналов и позволяющего осуществлять распараллеливание идентичных операций при формировании вектора адаптации.
Ключевые слова: адаптивная фазированная антенная решетка (АФАР), адаптивный решетчатый фильтр, пространственная фильтрация, диаграмма направленности антенны, корреляционная матрица, весовой вектор.
Abstract. The problem of clutter spatial filtering in a radar with an adaptive phased array was considered. The main quality criteria of spatial filter operation and direct computation methods for the optimal weight vector were determined. A variant was suggested for speeding the interference immunity system on the basis of an adaptive phased array at the expense of grid filtering algorithm improvement taking into account the persymmetric property of the sample correlation matrix of interference signals which allows to parallelize identical operations in forming the adaptation vector.
Key words: adaptive phased array, adaptive grid, spatial filtering, antenna pattern, correlation matrix, weight vector.
При большом числе воздействующих помех, как показано в [1], наиболее эффективным средством помехозащиты РЛС является адаптивная фазированная антенная решетка (АФАР), осуществляющая пространственную фильтрацию помех. Задача пространственной фильтрации в этом случае заключается в формировании таких пространственных характеристик антенны РЛС, при которых сигнал на ее выходе удовлетворял бы заданному показателю качества. Основными критериями качества работы пространственного фильтра, как показано в [1], являются следующие:
критерий максимума отношения сигнал/(помеха + шум) (МСПШ);
критерий минимума средней квадратической ошибки выходного полезного сигнала (МСКО);
критерий минимума средней мощности на выходе ФАР (МСМ).
И хотя теоретически все три критерия эквивалентны [1], с практической точки зрения интерес к различным критериям неодинаков, поскольку выбор критерия во многом определяется структурой построения системы и решаемыми ею задачами. Критерий МСКО представляется наиболее подходящим для связных РЛС с непрерывным или квазинепрерывным сигналом с известными параметрами. Критерий МСМ отличается принципиальной простотой и поэтому иногда используется при аналитических выкладках. Для радиолокационного применения наиболее пригоден критерий МСПШ, обеспечивающий при постоянстве уровня собственных шумов максимальную вероятность правильного обнаружения целей при заданной вероятности ложных тревог.
Оптимальное решение, определяющее оптимальный весовой вектор и соответствующее критерию МСПШ с точностью до скалярной константы, равно [1-3]:
При этом для решения задачи пространственной фильтрации могут использоваться следующие методы [1]:
метод непосредственного вычисления оптимального весового вектора Wопт по формуле (1) через оценку обратной корреляционной матрицы (КМ) входных сигналов антенной решетки;
градиентный метод оценки весового вектора.
Первый метод имеет ряд модификаций, отличающихся алгоритмом получения оптимального вектора:
вычисление весового вектора посредством формирования выборочной оценки КМ и ее непосредственного обращения с последующим вычислением весового вектора по (1);
вычисление весового вектора с использованием решетчатых фильтров без промежуточного этапа формирования КМ и ее непосредственного обращения [1, 3].
Основной недостаток метода вычисления весового вектора W посредством формирования выборочной оценки КМ и ее непосредственного обращения заключается в больших вычислительных затратах, требуемых для расчета весового вектора в крупноапертурных ФАР (в частности, по оценкам [3] при Nэл = 64 необходимо выполнить порядка 2∙10 комплексных операций), что не позволяет из-за ограниченной производительности используемых в РЛС ЭВМ проводить расчет Wопт за требуемое время tпэ.
Анализ быстродействия градиентного метода оценки вектора адаптации, проведенный в [2], показал, что время формирования Wопт в реальной РЛС ожидается равным 1/4 длительности ее такта (tт), а поэтому данный метод не обеспечит требуемую эффективность помехозащиты целевых каналов как в режиме сопровождения большого потока целей (требуемое быстродействие системы помехозащиты (tпз) должно быть не более 0,1 tт) , так и в режиме обнаружения близких целей (tпз £ 2 Rмин / с). Повышение оперативности времени расчета Wопт можно достигнуть, уменьшая канальность ФАР, или используя для расчетов ЭВМ с повышенным быстродействием. Однако уменьшение канальности приводит к пропорциональному уменьшению максимального числа одновременно компенсируемых помех, что делает невозможным использование данного способа. Создание супер-быстродействующих ЭВМ для РЛС в современных сложных экономических условиях также маловероятно. Поэтому рассмотрим другие способы повышения быстродействия АФАР. Таким способом может быть вычисление весового вектора с использованием решетчатых фильтров без промежуточного этапа формирования КМ и ее непосредственного обращения, применение которого для решения задач пространственно-временной обработки случайных сигналов основывается на работах [4,5].
Прежде всего, отметим, что типичная для практики априорная неопределенность параметров помех при решении уравнения RWопт = S0 преодолевается использованием тех или иных оценок корреляционной матрицы помех. Например, в отсутствие информации о какой-либо специфике в структуре матрицы, ее максимально правдоподобная оценка имеет вид [5]:
В соответствии с [3] оценку (2) можно заменить регуляризованной оценкой [3]:
при адаптивном формировании вектора весовой обработки
пространственного
(временного) фильтра Nэл-мерного сигнала ![]()
Здесь ![]() – Nэл-мерный вектор комплексной
огибающей i-ой обучающей выборки; k – объем обучающей выборки; I
– единичная матрица; b > 0 – скалярный параметр регуляризации; ψ
= R–1 – матрица, обратная оценочной корреляционной матрице помех; * –
знак эрмитова сопряжения.
– Nэл-мерный вектор комплексной
огибающей i-ой обучающей выборки; k – объем обучающей выборки; I
– единичная матрица; b > 0 – скалярный параметр регуляризации; ψ
= R–1 – матрица, обратная оценочной корреляционной матрице помех; * –
знак эрмитова сопряжения.
Адаптивный решетчатый фильтр (АРФ) представляет собой cпецвычислитель, структурно обеспечивающий оценку корреляционной матрицы R-1. Суть решения системы линейных уравнений с привлечением решетчатого фильтра заключается в последовательном исключении (обнулении) недиагональных элементов матрицы [5]. В качестве структурной схемы построения подобного спецвычислителя может быть взята схема параллелограмма без нормировки с комплексными числами [3], представляющая удачный компромисс по каноничности, универсальности и экономичности по составу и числу операций.
Указанная схема реализует факторизованное разложение оценки обратной корреляционной матрицы помеховых сигналов в соответствии с выражением:
где
– матрица "раздвоения" размерности 2Nэл × Nэл, превращающая вектор размерности N в вектор размерности 2Nэл с попарно одинаковыми элементами.
Матрица П – матрица перестановки, размерности 2N × 2N, имеющая вид:
где I2Nэл–1 – единичная матрица размерности 2Nэл – 1;
![]() – нулевой вектор-столбец размерности 2Nэл
– 1.
– нулевой вектор-столбец размерности 2Nэл
– 1.
Матрица П переставляет в матрице с 2Nэл строками первую строку вместо последней, а каждую из остальных строк – на место предыдущей.
В соотношении (5) матрица
весовых коэффициентов Aq (q = ![]() ) – блочно-диагональная матрица размерности 2Nэл
× 2Nэл с блоками размерности 2 × 2 вида:
) – блочно-диагональная матрица размерности 2Nэл
× 2Nэл с блоками размерности 2 × 2 вида:
где αiq, βiq – комплексные числа, Nэл – размерность задачи.
Матрица D представляет собой диагональную матрицу нормировок с действительными элементами, для которой справедливо соотношение:
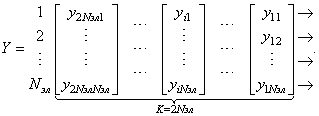
Для оценки корреляционной матрицы помеховых сигналов и вычисления вектора W в этом случае необходим пакет обучающих выборок размерностью Nэл × 2Nэл:
Быстродействие данного адаптивного решетчатого фильтра можно оценить, используя выражение [4]:
где k – размерность выборки (k = 2Nэл);
Nэл – количество приемных элементов АФАР.
C учетом быстродействия существующей на сегодня элементной базы (1 мкс) построенный на ее основе решетчатый фильтр затратит на расчет весового вектора, согласно (1), примерно ¼ tт, т. е. примерно столько, сколько тратится на расчет Wопт при использовании градиентного метода. Поэтому здесь также возникает необходимость поиска путей повышения быстродействия системы помехозащиты (ПЗ).
Специфика построения приемных антенн, как правило, влияет на вид и свойства получаемой корреляционной матрицы помеховых сигналов R. В частности, большинство РЛС имеет антенны с центральной симметрией размещения пространственно-временных каналов приема. По этой причине корреляционные матрицы помех, создаваемые внешними точечными источниками, на выходах антенной системы с идентичными амплитудными характеристиками каналов приема являются теплицевыми и персимметричными (симметричными относительно побочной диагонали) [6].
Знание вида матрицы и ее свойств в соответствии с [5] можно использовать для оптимизации алгоритма ее оценки с точки зрения скорости вычислений. В этой связи возникает вопрос разработки решений, учитывающих специфику построения приемных антенн большинства РЛС.
Рассмотрим алгоритм оценки корреляционной матрицы помех применительно к РЛС с АФАР.
Максимально правдоподобная выборочная оценка персимметричной матрицы, впервые полученная в [6], имеет вид:
![]() (12)
(12)
где нормирующая константа Ск (равная 1/2 k) не влияет на результирующие отношение сигнал/(помеха + шум) и в дальнейшем для простоты полагается равной единице;
![]() (13)
(13)
По сравнению с оценкой
(2) здесь дополнительно присутствует вторая матрица ![]() , представляющая собой результат поворота первой
относительно побочной диагонали. За счет этого матрица
, представляющая собой результат поворота первой
относительно побочной диагонали. За счет этого матрица ![]() (12) в целом является неотрицательно определенной
и персимметричной на произвольном шаге, в общем случае, неперсимметричных матрицах
слагаемых. Для оценки данной корреляционной матрицы помеховых сигналов и последующего
вычисления вектора W в этом случае необходим пакет обучающих выборок следующего
вида:
(12) в целом является неотрицательно определенной
и персимметричной на произвольном шаге, в общем случае, неперсимметричных матрицах
слагаемых. Для оценки данной корреляционной матрицы помеховых сигналов и последующего
вычисления вектора W в этом случае необходим пакет обучающих выборок следующего
вида:
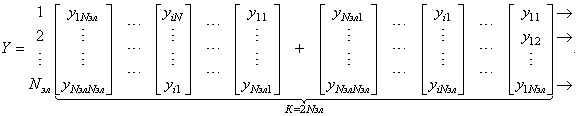 (14)
(14)
Следовательно, в процессе оценки корреляционной матрицы R необходимо последовательно осуществить обработку двух похожих матриц (14). В связи с идентичностью вычислительных операций представляется рациональным при решении задачи применить не последовательную, а одновременную обработку данных матриц, обеспечив параллельность вычислений за счет доработки существующего алгоритма решетчатой фильтрации.
В качестве такого способа оптимизации предлагается вариант распараллеливания вычислений за счет введения в состав алгоритма дополнительной операции усреднения весовых коэффициентов α и β.
В этом случае двойное использование каждой выборки эквивалентно удвоению числа независимых выборок при обучении АРФ. Поэтому для вычисления вектора Wопт нет необходимости использовать весь обучающий пакет, а достаточно лишь его половины. При этом места размещения блоков усреднения в структурной схеме АРФ определяются с учетом специфики второй матрицы.
Формулы усреднении коэффициентов α и β, реализующие данную идею, были выведены с использованием аппарата линейной алгебры (операций с матрицами) [7] и имеют следующий вид для "верхнего" и "нижнего" треугольника структурной схемы АРФ:
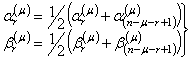 для "верхнего" треугольника АРФ;
для "верхнего" треугольника АРФ;
 для "нижнего" треугольника АРФ,
для "нижнего" треугольника АРФ,
где
![]()
![]()
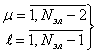 – номера каскадов АРФ (n = Nэл).
– номера каскадов АРФ (n = Nэл).
Так как длина обучающего пакета сокращается вдвое, то в соответствии с (11) скорость оценивания матрицы R–1 и формирования вектора адаптации Wопт удваивается [3].
Применительно к структуре
ранее рассмотренного адаптивного решетчатого фильтра поставленная цель может
быть достигнута тем, что в устройство, содержащее n(n – 1) элементарных
решетчатыx фильтров, n сумматоров, n блоков вычисления коэффициентов,
n блоков оценки нормировки, n блоков нормировки, n входов, n
выходов дополнительно введено n(n – 2) / 2, если n четно,
либо (n(n – 2) + l) / 2, если n нечетно, блоков усреднения коэффициентов
и n / 2, если n четно, либо (n – 1) / 2, если n нечетно, блоков усреднения нормировок.
Для такого варианта построения АРФ с целью получения эквивалентной по качеству оценки
![]() необходим вдвое меньший
объем выборок, т.е. требуется размерность объема выборок не n × 2n,
а всего лишь n × n (здесь n соответствует числу
каналов Nэл).
необходим вдвое меньший
объем выборок, т.е. требуется размерность объема выборок не n × 2n,
а всего лишь n × n (здесь n соответствует числу
каналов Nэл).
Таким образом, повышение быстродействия системы ПЗ на базе АФАР достигнуто за счет доработки алгоритма решетчатой фильтрации, учитывающей свойство персимметрии выборочной корреляционной матрицы помеховых сигналов и заключающейся в введении в алгоритм дополнительной процедуры, позволяющей осуществлять распараллеливание идентичных операций при формировании вектора адаптации.
Следовательно, корректный учет специфики построения АФАР современных РЛС с АФАР, в частности, учет центральной симметрии пространственно-временных каналов приема позволяет при оценке корреляционных матриц помех использовать решетчатые фильтры повышенного быстродействия, что вдвое увеличивает скорость работы систем помехозащиты РЛС.
Литература
1. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки. М.: Радио и связь. 1986.
2. Палий А.И. Радиоэлектронная борьба. М.: Воениздат МО СССР. 1974.
3. Курбатский С.А., Новиков А.В., Хомяков Д.А. Алгоритм вычисления вектора весовых коэффициентов в адаптивной антенной решетке // Известия ТулГУ. Вып.11. Часть 1. Тула: ТулГУ. 2012. С. 261-268.
4. Леховитский Д.И., Зарицкий В.И., Раков И.Д., Седышев Б.Г., Ратынский М.В. Методы адаптивной решетчатой фильтрации в задачах пространственно-временной обработки сигналов. Препринт № 8610. М.: РТИ АН СССР. 1987.
5. Кузин С.С., Леховитский Д.И. Новая структура решетчатого фильтра и адаптивный алгоритм оценки его параметров. Радиотехника. 1989. № 6.
6. Зарицкий В.И., Кокин Д.И., Леховитский Д.И., Саламатин B.B. Рекуррентные алгоритмы адаптивной обработки при центральной симметрии пространственно-временных каналов приема. Радиофизика. 1985. Том XXVIII. № 7.
7. Гантмахер Ф.Р. Теория матриц. М.: Наука. 1988.
8. Панченко Г. В., Новиков А.В., Манаенков Е.В. и др. «Двухзеркальная антенна» МПК8 Н 01 G 19/18(2006.01). Патент 121085 РФ. Изобретения. Полезные модели. 2012. № 28.
9. Василишин В.И. Устранение неоднозначности при оценивании угловых координат модифицированным унитарным алгоритмом esprit. Прикладная радиоэлектроника. 2009. Том 8. № 4. С. 553-560.
 (6)
(6)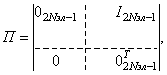 (7)
(7)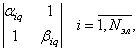 (8)
(8) (10)
(10)