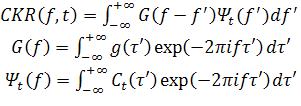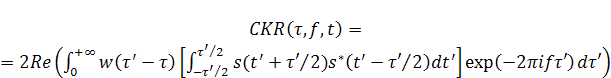Анализ гиперсинхронизации структур головного мозга во время эпилептических разрядов на основе специальных конических представлений ЭЭГ сигнала.

УДК 004.93'11

АНАЛИЗ ГИПЕРСИНХРОНИЗАЦИИ СТРУКТУР ГОЛОВНОГО МОЗГА ВО ВРЕМЯ ЭПИЛЕПТИЧЕСКИХ РАЗРЯДОВ НА ОСНОВЕ СПЕЦИАЛЬНЫХ КОНИЧЕСКИХ ПРЕДСТАВЛЕНИЙ ЭЭГ СИГНАЛА

В. Е. Анциперов¹, Ю. В. Обухов¹, Г. Д. Кузнецова², В. В. Гнездицкий³¹Институт радиотехники и электроники им. В.А. Котельникова РАН

²Институт высшей нервной деятельности и нейрофизиологии РАН

³ Научный центр неврологии РАН

Статья получена 25 ноября 2014 г.

Аннотация. В данной работе развивается ранее предложенный подход к задачам оценки ритмов головного мозга. Для анализа эпилептических разрядов, находящихся в центре внимания работы, предложенное ранее однопараметрическое (частотное) представление расширено до двухпараметрического (масштабно-частотного). Сделано это на основе аргументированной модели эпилептических разрядов как класса широкополосных импульсных сигналов с переменным ритмом следования и, возможно, изменяющейся формой импульсов. Проведена двусторонняя интерпретация распределения – спектральная, на основе аналитических спектров, и временная на основе многомасштабной оценки АКФ. Приведены полученные на основе предложенного подхода результаты анализа реальной, содержащей фрагмент эпилептического разряда ЭЭГ записи.

Ключевые слова: частотно−временной анализ ЭЭГ, эпилептические разряды, многомасштабный корреляционный анализ, аналитические спектры.

Abstract: In this article, we develop the previously proposed approach to the problem of cortical rhythms detection. For the analysis of epileptic discharges, which are the focus of the work previously proposed one-parameter (frequency) representation is extended to the two-parameter (scale-frequency). This was done on the basis of reasoned model of epileptic discharges as a class broadband pulse signals with variable rhythm and repetition, perhaps changing the pulse shape. Bilateral interpretation of developed distribution - spectral, based on analytical spectra and time based on multi-scale assessment of the ACF is under discussion. At the end of the article we present the results of the analysis of real containing a fragment of an epileptic discharge EEG record.

Key words: time−frequency EEG analysis, epileptic discharge, multiscale correlational analysis, analytic spectra.

Введение

В современной медицине, успешно решающей задачи, еще столетие назад казавшиеся труднопреодолимыми, проблемы лечения или даже облегчения протекания эпилепсии далеки от удовлетворительного решения. Сегодня в мире из 50 миллионов человек, страдающих эпилепсией, 35 не имеют необходимого лечения. Это связано либо с отсутствием соответствующих услуг, либо с тем, что эпилепсия не рассматривается как излечимое заболевание головного мозга. Для координации усилий в этом направлении в 1997 году стартовала Глобальная кампания против эпилепсии, задачи которой отражены в декларации [1].

Эпилепсия представляет собой внезапные периодические сбои в работе головного мозга, связанные с гиперсинхронизацией электрической активности нейронов. Отличительной чертой эпилепсии являются повторяющиеся приступы–разряды. Приступы возникают случайно, нарушая непредсказуемым образом нормальное функционирование мозга. Разряды, в зависимости от степени участия различных отделов головного мозга, условно могут быть разделены на две основные категории: фокальные (локализованные) и генерализованные. Генерализованные охватывают большинство областей головного мозга, тогда как фокальные затрагивают лишь отдельные участки, часто называющиеся эпилептическими очагами.

На Рис.1 приведен пример фрагмента ЭЭГ записи с явно различимым фокальным разрядом. Отметим здесь, что эпилептические разряды не всегда себя выговаривают так явно, зачастую их трудно отличить от других проявлений спонтанной активности мозга. Вместе с тем, например, успешное хирургическое лечение эпилепсий требует точной локализации эпилептического очага и его разграничения с функционально важными областями мозга.

Рис. 1. Пример эпилептического разряда (фокального приступа) в ЭЭГ записи: частота дискретизации 200 Гц, по горизонтальной оси номера отсчетов сигнала, по вертикальной − мкВ [2].

В настоящее время основными средствами нейровизуализации, используемыми для обнаружения эпилептических разрядов, являются ЭЭГ (электроэнцефалография), МЭГ (магнитоэнцефалография), а в последнее время еще и МРТ (магнитно-резонансная томография). Однако количество машин МРТ ограничено, они являются дорогостоящими и сканирование с их помощью занимает много времени. От MEG, с другой стороны, ввиду чувствительности к подвижности больного, другим артефактам, трудно добиться четких данных, особенно в умеренных и тяжелых случаях. Таким образом, ЭЭГ остается хотя и более грубым, но наиболее полезным и экономически эффективным методом для изучения эпилепсии. И хотя известные эксперты могут достаточно надежно, невооруженным глазом определить наличие эпилептических разрядов (особенно генерализованных, большой длительности), все больше возрастает потребность в разработке и широком внедрении ориентированных на среднего специалиста компьютерных средств и инструментов обнаружения признаков эпилепсии, благо цифровые энцефалографы сегодня уже не являются редкостью [3].

В данной работе мы приводим результаты развития МКА [4,5] применительно к задачам обнаружения и мониторинга ритмов коры головного мозга человека. Эти результаты публикуются впервые, поскольку были получены буквально в последнее время. В частности, ниже мы обсуждаем усовершенствование техники вычисления частотно-временных представлений “конического” типа (являющихся частным случаем корреляционных распределений) на основе недавно введенной нами концепции аналитических спектров [6,7]. Отметим, что предлагаемый нами подход ориентирован в первую очередь на обнаружение и мониторинг колебательной активности нейронов в широких частотных диапазонах, нежели на оценивание индивидуальных частот.

1. Гиперсинхронизация нейронных подсетей во время эпилептических разрядов

На сегодняшний день понимание механизмов сбоев нейронной сети головного мозга, вызывающих периодические эпилептические приступы, остается ограниченным. Считается, что основной причиной является нарушение баланса между возбуждением и торможением групп нейронов. При этом причиной такого дисбаланса могут быть самые различные патологические процессы: нарушение внеклеточного ионного гомеостаза, энергетического обмена, изменение функций нейрона как приемника или передатчика нервных импульсов и т.д. Однако, несмотря на значительные различия в этиологии, проявление дисбаланса почти всегда одинаково – синхронная пачечная активность корковых нейронов (см. Рис.2). Поэтому эпилептические приступы локализуются и подразделяются, как правило, по наблюдениям электрической активности коры, нежели по лежащей в ее основе патофизиологии.

Рис. 2. Потенциалы локального поля и внутриклеточные потенциалы эпилептического разряда, записанные с корковой области находящейся под анестезией кошки. Вверху записи пяти отведений потенциалов локального поля, снятые электродами с поверхности коры и из объема с разной глубины. Расстояние между электродами 0.4 мм. Сразу под ними расположена запись внутриклеточный активности отдельного нейрона, расположенного на глубине 1 мм и на расстоянии 0.5 мм от линии указанных выше электродов. Характерные пик-волновые колебания (spike–wave) и быстрые колебания (fast runs) показаны в увеличенных масштабах внизу рисунка. Серым цветом отмечены фрагменты пика и волны. [8].

Так же, как задающие такт генераторы в искусственных нейронных сетях, некоторые корковые клетки периодически, на вполне определенных частотах, генерируют пачки импульсов (bursts of spikes). Эти нейроны способны служить пейсмейкерами – генераторами ритмов для синхронизации колебаний других нейронов в сети, и генерируемые ими пачки импульсов способны, по-видимому, даже приводить к резонансным явлениям в подсетях. В коре головного мозга наблюдались по крайней мере два типа таких нейронов. Это, во-первых, пирамидальные клетки гиппокампа, а, во-вторых, пирамидальные клетки 5 слоя неокортекса. Отмеченные нейроны обычно демонстрируют ритмическую пачечную активность в диапазоне частот 4-15 Гц. Длительность пачек зависит от скорости восстановления, которая регулируется процессами открытия-закрытия кальциевых и натриевых каналов. Активируемые кальцием калиевые токи (с постоянной времени ~ 100 мс) прекращают генерацию спайков и контролируют время восстановления после генерации, т.е. контролируют частоту колебаний [9].

Проявления пачечной активности на ЭЭГ у здоровых людей наблюдается не часто: в некоторых стадиях сна, при медикаментозных воздействиях и т.д. [10]. Однако, в случае эпилепсии, ввиду резонансной синхронизации больших участков головного мозга – гиперсинхронизации, даже при существенной низкочастотной фильтрации сигнала на поверхности скальпа [6], пачечная активность себя проявляет в виде колебаний разных видов (см. Рис.2 и Рис.1). Наиболее типичными для разрядов являются формы колебаний типа: острая волна, острый пик, пик-(плавная)волна и пики-(плавная)волна [11].

В любом случае можно сказать, что типичным признаком эпилептических разрядов являются последовательности следующих подряд эпилептиформ. Иногда говорят о частоте их следования, например о диапазонах в 2-3.5 Гц или реже о 4-7 Гц, но в строгом смысле этого слова разряды не являются периодическими колебаниями, поскольку ритм следования эпилептиформ меняется в зависимости от стадии разряда. Сослаться на то, что эпилептические разряды являются узкополосными колебаниями, тоже было бы не правильно, поскольку они обладают широким спектром.

Поэтому, ввиду вышеизложенного, наилучшей моделью, к которой можно было бы отнести эпилептические разряды, является с нашей точки зрения класс широкополосных импульсных сигналов с переменным ритмом следования импульсов и, возможно, меняющейся формой импульса. Ниже для этого класса сигналов приводятся разработанные нами средства анализа, и обосновывается интерпретация возможных результатов анализа с точки зрения присущих сигналам характеристик.

2. Частотная и многомасштабная интерпретации квадратичных конического вида представлений широкополосных сигналов вида эпилептических разрядов

В предыдущей работе [6] нами подробно обсуждалось квадратичное частотно−временное представление (ЧВП) конического типа CKR (cone−shape kernel representation [12]), известное также как представление Дзао−Атласа−Маркса:

(0)

и его интерпретация как средства анализа в заданных частотных диапазонах взаимной корреляции аналитических спектров (в общем случае комплексного) сигнала (вид представления (0) соответствует введенному в [13] для параметра ).

Отметим, что формально к виду (0) можно отнести и другие известные распределения (ЧВР) такие, как распределение Чои−Вильямса или Баттерворта (аппроксимировав конечный интеграл в (0) бесконечным, с гауссовым или экспоненциальным окном), распределение Борна–Жордана и целый ряд их аналогов и обобщений (см., например, [14] ). Это большое семейство распределений обычно определяется как семейство с подавленной интерференцией компонент (RID − Reduced Interference Distributions). Оно характеризуется тем, что его представители хорошо подчеркивает нестационарности и переходные процессы связанные, в частности, с перестройками спектрального состава сигнала. Содержательный обзор преимуществ RID в применениях к анализу биологических сигналов можно найти в [15]. Формальная схожесть CKR с распределениями RID−семейства обеспечивает его многими положительными качествами этих распределений и может составлять содержание первой, классической интерпретации CKR как представления с хорошо подавленной интерференцией.

Вместе с тем, как было показано в [12], в отличие от отмеченных RID−распределений, CKR (0), ввиду отсутствия в нуле сингулярности у его весовой функции , не является в буквальном смысле распределением энергии сигнала. Действительно, поскольку распределения Чои−Вильямса, Баттерворта, Борна–Жордана − все характеризуются сингулярностью вида в нуле, интеграл от них по всей f−t плоскости равен энергии сигнала. Для CKR же интеграл, например, по оси частот f всегда, при любых t обращается в нуль, поэтому, и в плоскости f−t он будет равен нулю. Отсутствие нормировки послужило поводом определять CKR именно как представление (representation), а не распределение (distribution), что иногда приводит к некоторым терминологическим неудобствам. Впрочем, свойство регулярности имеет и свои преимущества: переход к спектральным представлениям оказывается естественным, не требующим специального обоснования.

Предполагая таким образом, что ввиду ее регулярности имеет спектр и применяя к правой части (0) теорему о спектре произведения функций, получим:

, (1)

где есть стоящая в квадратных скобках в (0) автокорреляция сигнала. Если, как и в [6], ввести связанные с текущим моментом времени аналитические спектры локального будущего и локального прошлого сигнала:

, (2)

то, после ряда преобразований, получим:

, (3)

что, в наиболее частых для практики случаях действительной и симметричной весовой функции , имеющей действительный и симметричный спектр , дает представление:

(4)

− главный, полученный в предыдущей работе результат.

Представление (4) задает вторую, спектральную интерпретацию CKR, которая может быть раскрыта следующим образом. Пусть имеется интервал времени длительности 2T с центром в , где сигнал ведет себя квазистационарно. Аппроксимируя аналитические спектры (2) интегралами с конечными верхними пределами T, выразим их через (нормированные) оконные преобразования Фурье [10]:

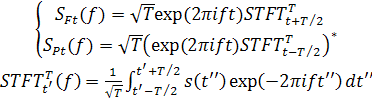(5)

Из (5) легко заметить, что сумма также выражается через оконное преобразование Фурье, но с удвоенной шириной окна − . Взяв от этой суммы модуль в квадрате и используя обозначение для классической спектрограммы [10], после элементарных преобразований получим:

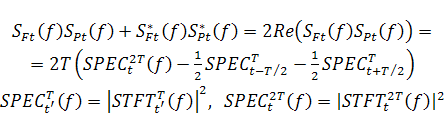. (6)

В силу сделанного предположения о квазистационарности, спектрограмма в интервале слабо зависит от (что можно было бы принять в качестве определения используемого здесь условия квазистационарности). С учетом этого замечания:

, (7)

для квазистационарного поведения сигнала подстановка (7) в (4) приведет к:

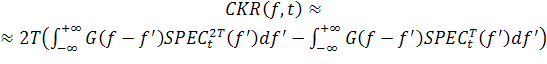. (8)

Если носитель спектрального окна захватывает полосу сигнала и на ней окно является плоским (~ постоянным), то оба члена в правой части (8), ввиду нормировки спектрограмм на мощность сигнала, взаимно сократятся и CKR будет нулевой. Поэтому, чтобы представление (4) несло содержательную информацию о сигнале, окно должно иметь осциляторный вид. Действительно, такие окна подчеркивают детали обрабатываемых функций, а спектрограммы и отличаются именно в мелких деталях (связанных с разным разрешением). Учитывая условия действительности и симметрии для спектральных окон, выберем в виде:

, (9)

где – действительная, симметричная огибающая с плавным поведением на носителе размера , равного ширине анализируемого диапазона частот, а (точнее ) характеризует степень “осциляторности” . Подставляя (9) в (4), получим для CKR следующий уточненный вид:

. (10)

Из (10) следует, что содержательная интерпретация CKR сводится по существу к анализу косинус преобразования выделенной окном в диапазоне произведения аналитических спектров локального будущего и локального прошлого сигнала. Параметр выступает при этом как анализируемая “частота” частотного поведения произведения.

Исходя из полученного вида представления CKR (10) нетрудно понять следующее. Как с вычислительной, так и с концептуальной точек зрения было бы полезно расширить CKR от исходного (0) представления, заданного при некотором параметре , до семейства представлений с изменяющимися в некотором диапазоне параметрами. Другими словами, целесообразно расширить CKR от однопараметрического (частотного) представления до двухпараметрического масштабно–частотного представления (10).

При этом целесообразно яснее, нежели чем формальное определение “частота частоты”, понимать смысл параметра . С этой целью, во–первых, заметим, что размерность есть размерность времени, поэтому определение его как некоторого (временного) “масштаба” правомерно. А, во–вторых, чтобы понять с какими особенностями сигнала может быть связан этот масштаб, вернемся во временную область, обращая преобразования (2) и подставляя результат в (10):

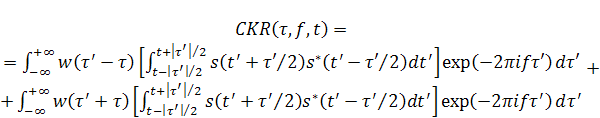, (11)

где – обратное Фурье–преобразование огибающей спектрального окна:

. (12)

Представление (11) задает третью интерпретацию CKR отчасти похожую на первую, но отличающуюся тем, что в ней спектральный анализ автокорреляции сигнала осуществляется локально – под окном (12) шириной , смещенным на величину по оси времени. Отметим, что поскольку в наиболее интересном случае, когда и полностью лежат на положительной и отрицательной осях соответственно, в соотношении (11) можно ограничиться интегрированием по этим полуосям и, после замены знака переменной интегрирования во втором слагаемом, получить:

. (13)

Смысл интерпретации (13) для широкополосных импульсных сигналов сразу же становится ясным, если заметить, что стоящая в квадратных скобках автокорреляция сигнала является с точностью до нормировки оценкой корреляционной функции процесса, именно многомасштабной АКФ, введенной нами ранее в [4] и свойства которой подробно исследованы и изложены в [5]. Для импульсных процессов огибающая АКФ помимо основного максимума при нулевом смещении содержит также боковые максимумы, имеющие удвоенную ширину (импульсов) и смещённые по оси на расстояния между текущим и следующим, через одного и т.д. соседями. Если окно (вместе с модулирующей ) по форме похоже на ковариацию форм импульсов (эпилептиформ), то свертка (13) с этим окном, представляя собой некоторый вариант хорошо известной из локации согласованной фильтрации, только подчеркнет эти максимумы (и подавит паразитные).

Таким образом, полученное представление (13) потенциально должно быть подходящим средством анализа эпилептических разрядов. При этом, исходя из интерпретации (13), положения боковых импульсов огибающей CKR должны оценивать интервалы между ближайшими к текущему моменту времени импульсами – локальный ритм разряда, колебания несущей CKR – доминирующую частоту спектра эпилептиформ.

В соответствии с изложенным, (13) является подходящим средством анализа ритма, если доминирующая частота и длительность окна предварительно оценены. Если нет, то целесообразно обратиться к спектральной интерпретации (10) и оценить и по форме произведения аналитических спектров. Правда эти оценки теперь могут зависеть от возможно неизвестного , но тогда для анализа придется прибегнуть к методам последовательных приближений.

Последнее по порядку, но не по важности относится к исходной интерпретации CKR как RID представления: в отношении времени (13) должно давать очень хорошее разрешение переходных процессов, в частности начала и окончания разрядов.

С целью проверки перечисленных выше утверждений нами был проведен численный анализ средствами MatLab реальных записей пациентов с эпилепсией, результаты которого приводятся ниже.

3. Многомасштабная интерпретация конического представления для эпилептических разрядов

Анализ реальных данных разработанными и представленными выше средствами производился на основе небольшой аннотированной базы данных (3 пациента с генерализованной, 3 – с фокальной эпилепсией), предоставленной Научным центром неврологии (ранее НИИ неврологии) РАМН, в лице одного из соавторов статьи – Гнездицкого В.В.

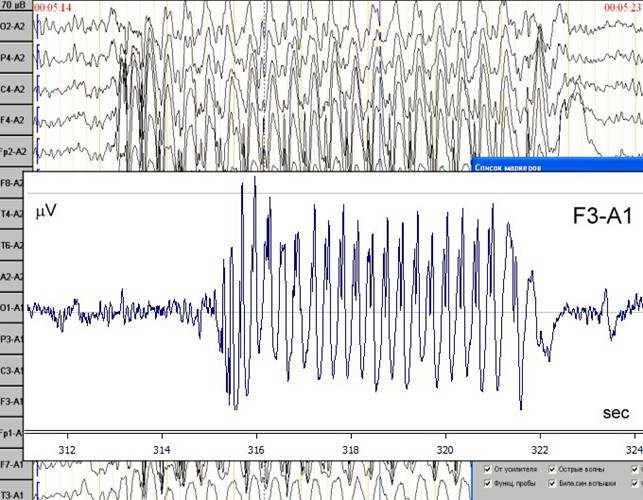
Рис. 3. Фрагмент реальной ЭЭГ записи, содержащей хорошо выраженный ~7 сек. генерали-зованный эпилептический разряд. В качестве примера представлено отведение F3-A1.

В данной работе, с целью иллюстрации, выбран один из пациентов – N, 30 лет с диагнозом “генерализованная эпилепсия” (с 12 лет). На рис. 3 представлено одно из отведений – F3-A1 на временном участке записи, содержащем хорошо выраженный генерализованный эпилептический разряд (скриншот приложения визуализации данных представлен в качестве фона рисунка). Разряд длится ~ 7 сек с ~315 до ~322 сек. Частота дискретизации сигнала 200 Гц. В дальнейшем обсуждается именно этот фрагмент ЭЭГ записи.

На рис. 4 для текущего момента времени = 218 сек представлены рассчитанные по формулам (2) модули аналитических спектров и (на центральном графике) и спектр (1) автокорреляции .

Рис. 4. Фрагмент анализируемого сигнала (вверху), мощности аналитических спектров и (в центре) и, вычисленный по ним спектр автокорреляции (внизу).

Спектр автокорреляции вычислен по найденным аналитическим спектрам в соответствии с формулой (3). Аналитические спектры рассчитывались по 2.5 сек фрагментам (512 моментов отсчетов для ПФ) текущего будущего и прошлого сигнала (future и past), отмеченных на верхнем графике рис. 4 цветами.

На рис. 5 для текущего момента времени = 218 сек представлены (нормированные на ) автокорреляция , как обращение спектра (см. определение (1)) и представление как обращение сдвинутого на и взвешенного посредством спектра (10).

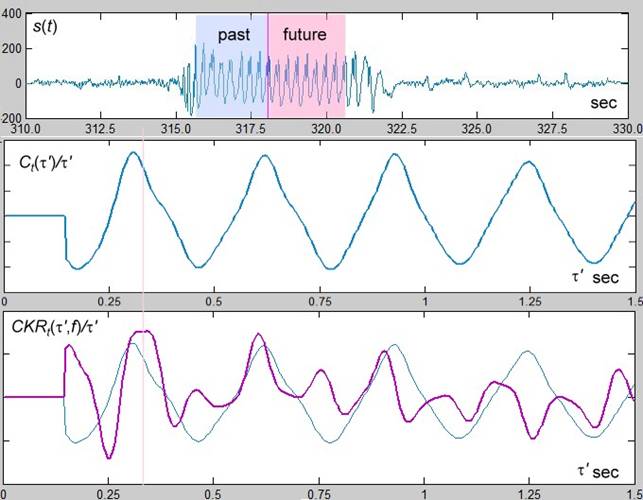
Рис. 5. Фрагмент анализируемого сигнала (вверху), (нормированная на ) автокорреляция (в центре) и, найденное для заданной частоты при переменном параметре CKR (13) (внизу на фоне ).

Вычисление для рассматриваемого примера осуществлено для Гц, окно было выбрано Гауссовой формы с полушириной Гц. Вертикальной линией выделен хорошо выраженный на обоих графиках боковой максимум ~ 0.31 сек (~3.2 Гц). Этот максимум, как изложено выше, вполне может соответствовать периоду следования импульсов (пачек спайков) во время разряда.

Рис. 6 и Рис. 7 демонстрирую общую панораму представлений – первый для автокорреляционной, связанной с многомасштабным анализом (МКА) функцией , второй для обсуждаемого в работе представления (13) (локальные версии которых представлены на Рис.5). Отметим неоднократно отмеченную выше способность представлений подчеркивать границы резких перестроек спектра.

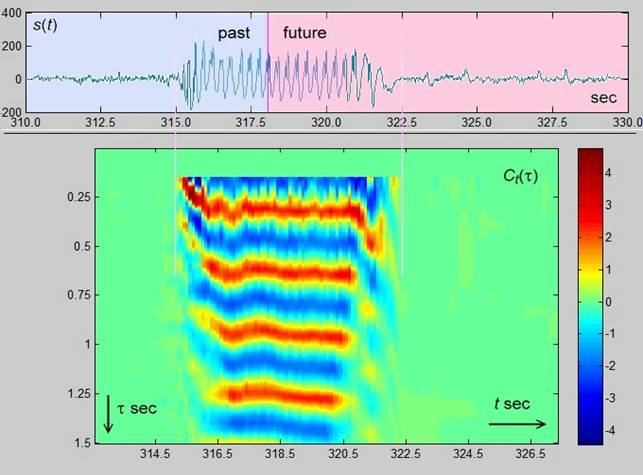
Рис. 6. Панорамное представление эпилептического разряда с помощью МКА АКФ .

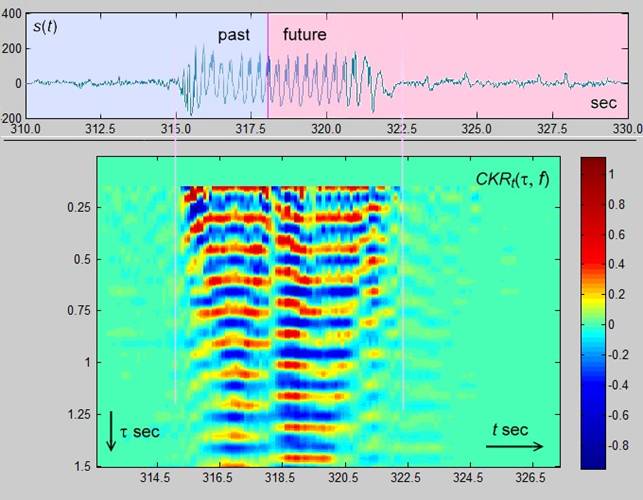
Рис. 7. Панорамное представление эпилептического разряда с помощью (13) при Гц., Гц.

Выводы

В данной работе, исходя из предложенного ранее [6] для анализа ритмов ЭЭГ, известного конического типа распределения Дзао−Атласа−Маркса (0) выведено двухпараметрическое распределение (также конического типа) (13). Этот вывод осуществлен в соответствии с обоснованной моделью эпилептических разрядов как класса широкополосных импульсных сигналов с переменным ритмом следования и, возможно, изменяющейся формой импульсов. Проведена двусторонняя интерпретация распределения – спектральная (10), на основе аналитических спектров (2) и временная (13) с помощью многомасштабной оценки АКФ [4]. В рамках изложенных интерпретаций уточнен смысл параметров и как доминирующей частоты в спектре импульса (эпилептиформы) и, соответственно, ритма следования импульсов.

С целью проверки практической ценности полученного представления, оно было использовано для анализа реальной ЭКГ записи, содержащей фрагмент эпилептического разряда. Полученные результаты в большей своей части подтвердили теоретические выводы и возлагавшиеся на предложенный подход ожидания.

Мы надеемся, что изложенный метод найдет достойные приложения, как в исключительно важной на сегодняшний день области борьбы с эпилептическими заболеваниями, так и в более широкой, фундаментальной области исследования и понимания функционирования головного мозга.

Работа выполнена при финансовой поддержке Программы № 43 фундаментальных исследований Президиума РАН по стратегическим направлениям развития науки "Фундаментальные проблемы математического моделирования" и гранта РФФИ N 12-07-00104-а.

Литература

1. European Declaration on Epilepsy. 25 October 1998. [электронный ресурс]. URL: http://www.who.int/mental_health/media/en/82.pdf.

2. S. Sanei, J. Chambers. EEG signal processing. // John Wiley & Sons, Inc., 2007.

3. Обухов Ю.В., Анциперов В.Е. и др. Частотно-временной анализ электрической активности мозга при болезни Паркинсона // Нейродегенеративные заболевания. Фундаментальные и прикладные аспекты. Под ред. акад. М.В.Угрюмова. М: Наука, 2010, стр 112-129.

4. Анциперов В.Е. Многомасштабный корреляционный анализ нестационарных, содержащих квазипериодические участки сигналов. // “Радиотехника и электроника”, 2008 г., т. 53, № 1, стр.73-85.

5. Анциперов В.Е. Новый метод оценки корреляционных функций в задачах обнаружения и обработки радиолокационных и связных сигналов // Доклады III Всероссийской конференции “Радиолокация и радиосвязь”, Москва, 26-30 октября 2009 г, стр. 887-881.

6. Анциперов В.Е. Обнаружение ритмов головного мозга человека на основе корреляции аналитических спектров ЭЭГ в основных диапазонах частот. // Журнал радиоэлектроники [электронный журнал]. 2014. №5. Режим доступа: http://jre.cplire.ru/jre/may14/13/text.pdf.

7. Анциперов В.Е. Использование аналитических спектров локального прошлого и будущего сигнала для формирования и анализа билинейных частотно-временных представлений // Доклады 16-й Международной Конференции “ Цифровая обработка сигналов и ее применение DSPA-2014”, т.1, ISSBN 978-5-905278-01-3, Москва, 2014, стр. 113-117

8. M. Bazhenov, I. Timofeev et al. Cellular and network mechanisms of electrographic seizures. // Drug Discov Today: Disease Models, Vol. 5, No. 1, 2008, pp. 45-57.

9. Xiao-Jing Wang. Neurophysiological and Computational Principles of Cortical Rhythms in Cognition. // Physiol. Rev. Vol. 90, No.3, 2010, pp. 1195–1268.

10. Жадин М.Н. Биофизические механизмы формирования электро-энцефалограммы. // М.: Наука, 1984.

11. D. Y Ko. Epileptiform Discharges. // Medscape Reference, WebMD, LLC, Apr 2, 2014, [электронный ресурс]. URL: http://emedicine.medscape.com/article/1138880-overview#showall

12. F. Hlawatsch, T. Manickam, R. Urbanke and B. Jones. Smoothed pseudo-Wigner distribution, Choi-Williams distribution, and cone-kernel representation: Ambiguity-domain analysis and experimental comparison. // Signal Processing, vol. 43, p. 149-168, 1995

13. Zhao Y., Atlas L. E., and Marks R. J. The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals. // IEEE Trans. Acoustics, Speech, Signal Processing, V. 38, N 7, 1990, pp. 1084–1091.

14. Time-frequency analysis: concepts and methods. Edited by F. Hlawatsch and F. Auger. // GB and US: ISTE Ltd and John Wiley & Sons, Inc., 2008.

15. W.J.Williams. Reduced Interference Distributions: Biological Applications and Interpretations/ // Proceedings of the IEEE, Vol. 84, No. 9, 1996, pp. 1264-1280.