Стохастическая радиолокация: условия решения задач обнаружения, оценивания и фильтрации

 

Ю. Н. Горбунов

ИРЭ им. В.А. Котельникова РАН, Фрязинский филиал

Статья получена 22  октября 2014 г.

 

Аннотация. Рассматривается стохастический подход к решению традиционных задач радиолокации: обнаружения, оценивания, фильтрации. Стохастическая радиолокация базируется на концепции внедрения в процесс обработки и формирования радиолокационных сигналов искусственной стохастичности, предполагающей  наряду с естественной стохастичностью, обусловленной случайной природой входных сигналов,  рандомизацию условий процесса «приём – передача». Это -  введение в процессе наблюдения цели в параметры схем обработки и  формирования сигналов случайных параметров, процедур и компонент. Примерами могут служить: вобуляция частоты повторения, перестройка несущей частоты, модуляция порогов квантования, использование стохастических шкал квантования и измерения, использование эталонных случайных добавок и т.п. В статье анализируются условия решения ключевых задач радиолокации -  обнаружения, оценивания и фильтрации и приводятся конкретные примеры технических приложений относящихся к новому направлению «стохастическая радиолокация».

Ключевые слова: стохастическое аналого-цифровое преобразование, селекция движущихся целей, рандомизация, стохастическая дискретизация времени и пространства, шумовая радиолокация.

Abstract. We consider the stochastic approach to solving the problems of traditional radar: detection, estimation, filtering. Stochastic radar is based on the concept of implementation in the processing and formation of radar signals artificial stochasticity, assuming along with the natural stochasticity, due to the random nature of the input signals, the randomization process conditions "technique - transfer". This is - an introduction to the process of monitoring objectives and parameters processing circuits signal generating random parameters, procedures and components. Examples are: the wobble frequency of repetition rearrangement carrier frequency, modulation quantization thresholds, the use of stochastic quantization scales and measuring, using standard random additives, etc. This article analyzes the conditions for resolving the key tasks of radar - detection, estimation and filtering, and provides concrete examples of technical applications relating to the new field of "stochastic radar."

Keywords: stochastic analog-to-digital conversion, the selection of moving targets, randomization, stochastic sampling of time and space, the noise radar.

 

Введение и постановка задачи

В [1] дан обзор развития стохастических когерентно-импульсных РЛС с СДЦ: от первого внедрения в них режимов псевдослучайной вобуляции частоты повторения зондирующих импульсов для устранения эффекта «слепых скоростей» до рандомизации приема сигналов, реализации принципов стохастического принятия решений, стохастического «обеления» пассивных и активных помех и в перспективе - полномасштабного применения сверхширокополосной (СШП) шумовой радиолокации реализующей форму функции неопределенности удовлетворяющей требованию круговой симметрии. В [1] отмечено, что исследования на тему «современная радиолокация» безусловно в первую очередь идут по пути выбора вида зондирующих сигналов и совершенствования методов и средств цифровой, в общем случае пространственно-временной (ПВ, «the spatial time processing» SP) обработки эхо-сигналов в когерентно-импульсных РЛС с системой СДЦ (класс РЛС «coherent pulsed radar» с системой СДЦ  «system moving target indication»  MTI).

Актуальность исследований заключается во внедрении в технику обработки и формирования РЛ сигналов новых цифровых технологий, поднимающих радиолокацию на новый современный уровень. Это:

- использование когерентно-импульсных зондирующих сигналов (последовательностей) со случайными параметрами (периодом повторения, несущей частоты, фазой квантования и т. д.), дающих прирост «стохастичности» в стремлении реализации преимуществ СШП радиолокации по сравнению с традиционной узкополосной радиолокацией с детерминированными сигналами;

- реализация распределённой системы пространственно-временной (ПВ) обработки  в когерентно-импульсных РЛС с СДЦ и фазированными антенными решетками (ФАР), осуществляющей доплеровско - угловую селекцию целей на фоне мощных активных (АП) и пассивных (ПП) помех с помощью адаптации приема и подавления помех с помощью формирования «нулей» в амплитудно-частотной характеристике (АЧХ) системы СДЦ и диаграмме направленности антенны (ДНА)  ФАР РЛС;

- реализация адаптивного приёма и формирования сигналов в условиях произвольных помех и большой неопределенности в выборе параметров сигнала и способов их обработки;

- повышенная скрытность работы РЛС с реализацией сниженного уровня заметности защищаемого объекта.

Цифровой обработке (ЦО), несмотря на известные преимущества, присущи недостатки: наличие  эффектов стробоскопического характера («слепые фазы», «слепые направления», «слепые скорости»), нелинейностей амплитудных характеристик типа  «зона нечувствительности», «люфт», «жёсткое ограничение», наличие шумов квантования,  округления  и т.п., которые обычными способами, вытекающими из классической теории ПВ обнаружения учесть не удается.

При устранении указанных недостатков в авиационных и космических РЛС для получения гарантированных решений необходимо учитывать не только ограничения по определению области предсказания в выборе и параметров сигналов, но и ресурсные ограничения: разрядность, частоты квантования, размеры окон ПВ выборок, размеры областей предсказания и многообразие способов устранения априорной неопределенности.

В работах [3-7] и других российских и зарубежных авторов исследованы вопросы анализа и синтеза цифровых устройств и алгоритмов ПВ обработки РЛ сигналов, однако специальные разделы, относящиеся к устранению вышеуказанных недостатков исследованы недостаточно. Малоразрядной (МР) цифровой обработке в условиях вышеупомянутых ресурсных ограничений посвящена работа [8]. Эти ограничения проявляются в современных авиационных и космических РЛС, где система ЦО, в особенности для РЛС с ФАР, представляет собой достаточно разветвленную сеть (многопроцессорную, многоканальную).

 При параллельной обработке информации (на регистровом и топологическом уровнях, в параллельных интерфейсах) разрядность информационных потоков радиолокационных данных напрямую определяет техническую сложность построения аппаратуры (фазовращатели, умножители, процессоры, нормализаторы задержек). Поэтому разрядность РЛ данных, частоты дискретизации, размеры окон ПВ выборок должны быть минимальными. Представленный в [8] обзор и начатый ещё в 90-х годах [9] и продолженный  в [10] подход к оформлению направления представляет собой по существу набор методов и средств рандомизированной обработки (см. список литературы [8]), однако чётко сформированной теории цифровой рандомизированной обработки («стохастической радиолокации») в открытой печати не было.

Термин randome (случайный) предполагает искусственное введение случайностей (случайные пороги, случайные аддитивные учитываемые добавки, случайные весовые коэффициенты и др.) в процедуру обеления шумов квантования, обусловленных дискретизацией. Процедуры подобного типа известны в литературе, однако систематизированное и научное изложение данного вопроса на сегодня разработано недостаточно. Сегодня на основе такого подхода на сегодня создан целый ряд конкретных устройств, реализирующих различные способы обеления («рандомизации», «стохастической линеаризации», «накачки», «вобуляции» и т.п.).

Предложенный метод, базируется на идейной основе метода Монте-Карло и в рамках рассматриваемого подхода применялся при построении различных технических устройств.

 Цель настоящей статьи – сформулировать направление стохастической радиолокации с позиций классической теории обнаружения и оценивания параметров РЛ сигналов.
 

Теория цифровой стохастической обработки РЛ сигналов

Традиционную радиолокацию обычно не называют стохастической, но этот термин очень распространен (см., например, Сосулин Ю. Г. Теория обнаружения  и оценивания стохастических сигналов. - М.: Советское радио, 1978. – 320 с.). В этой работе рассматривается применение статистической теории к зашумленным и искаженным случайными помехами детерминированным сигналам. Реже применяются стохастические критерии (правила) для решения задач обнаружения и оценки параметров стохастических сигналов. 

В данном разделе проведем краткий анализ основ теории и результатов исследований в области обработки и формирования сигналов в РЛС с селекцией движущихся целей (СДЦ) с применением методов рандомизации грубых статистик [8], когда стохастичность искусственно и целенаправленно закладывается в модели сигналов и алгоритмы их обработки.

 Обобщение работ по анализируемому направлению позволяет представить структурную схему теории стохастической радиолокации, которая приведена на Рис. 1.

Теория цифровой стохастической обработки ПВ сигналов (теория стохастической радиолокации) сегодня до конца не разработана. Достигнутый уровень – это сформировавшаяся совокупность идей, способов, устройств, алгоритмов.   Идейной основой теории стал метод Монте-Карло, ранее применявшийся в основном в вычислительной математике и моделировании. Адаптация этого метода к обработке РЛ сигналов не явилась пионерским предложением и применительно к измерению дальности и построению МР систем СДЦ применялась ранее в разработках специалистов и автором настоящей статьи. Применительно к решению задач, выходящих за рамки теории ПВ обработки можно также упомянуть следующие имена: В.Г. Гайсов, Кан, Шапиро, А.К.Микельсон, Р.Ф. Немировский, И.Я. Билинский, Э.И. Вологдин, Г.П. Вихров, В.С. Гладкий, В.Г. Стругач, Ю.Г. Полляк, О.Н. Граничин, Б.Т. Полляк, В.И. Фомин и ряд других, известных в кругу  специалистов, применяющих рандомизацию для решения различных задач, включая задачи вероятностного моделирования.  

   

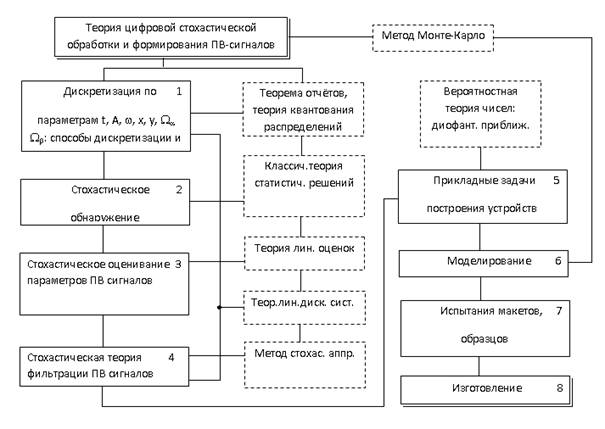
Рис. 1. Структурно-логический базис теории стохастической радиолокации

Первой важной структурной компонентой исторически сформировавшегося структурно-логического базиса теории стохастической радиолокации является компонента дискретизации и квантования. Это:

- квантование во времени , обусловленное периодической структурой когерентно-импульсного сигнала («медленное время» по пачке импульсов) и отдельных реализаций эхо-сигналов («быстрое время» по одному периоду зондирований);

- квантование пространства по осям  и  электромагнитного (ЭМ) поля в апертуре ФАР РЛС;

-        квантование по уровню амплитуды сигналов  и фазы сигнала в каналах ПВ фильтрации (в квадратурных каналах);

- квантование координат и параметров движения цели, каковыми могут быть дальность , пеленг  , скорость V (доплеровское смещение частоты );

- квантование обычных  и пространственных  и  частот в апертуре ФАР РЛС, что в свою очередь связано с квантованием угловых направлений по азимуту  и углу места ;

- квантование распределений, поскольку входной ПВ сигнал (поле) в процессе его наблюдения представляет собой случайный процесс, развивающийся во времени.

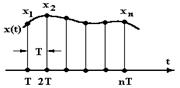
Квантование по времени превращает непрерывные функции (сигнала) x(t), в решетчатые функции x(nT), n = 0, 1, 2,… , где T – интервал временного квантования по каждой из квадратурных составляющих сигнала с выхода фазовых детекторов по видео или промежуточной частоте (см. Рис. 2).

 

а)

б)

Рис. 2. Квантование по времени: а – получение решетчатых функций;

б – эхо-сигналы в  N  зондированиях с периодом повторения Т

 

При обычной обработке дискретизатор во времени  это ключ, замыкаемый через  промежутки времени T, далее преобразователь уровня в двоичный код - аналого-цифровой преобразователь АЦП. Теорема отчетов определяет условия, при которых такое квантование возможно и потери информации отсутствуют. При стохастической обработке размеры ПВ выборок тесно связаны с самой процедурой дискретизации и квантования и порядком ЦФ, определяющим число степеней свободы, и, поэтому,  показана связь этого блока с блоками «Теорема отсчётов» и «Теория линейных дискретных систем».

Блок стохастического обнаружения ПВ сигналов предполагает рандомизацию обнаружения цели радаром, поскольку обеспечение инвариантности (независимости от распределения) в условиях нестационарных шумов и помех требует использования коротких «обучающих» выборок, непараметрической и ранговой статистики [11].

Стохастическое оценивание (измерение) параметров ПВ сигналов, которое в дальнейшем мы назвали «рандометрией», осуществляется отдельным блоком на схеме Рис. 1, хотя это выделение отражает особенности решения функциональных задач и не претендует на законченность их решения вне связей с соседними блоками.

Блок стохастической фильтрации ПВ сигналов поставлен третьим по ходу обработки ПВ сигналов, однако очевидно, что эта фильтрация может осуществляться как по высокой, так и по низкой частоте, т.е. после гетеродинирования.

Связь блоков «Прикладные задачи» и «Вероятностная теория чисел: диофантовые приближения» обусловлена, необходимостью исследования: аппаратурного вопроса формирования-воспроизведения (разыгрывания) рандомизирующего (хаотического) процесса с гарантируемыми характеристиками распределения, включая корреляцию.

При описании внутренних и внешних связей обратим внимание на внутреннее взаимодействие блоков «квантования», «обнаружения», «оценивания» и «фильтрации» в чисто описательном плане. Эта совокупность блоков имеет две внешние связи с теорией линейных дискретных систем, т.е. предполагает использование принципа суперпозиции сигнальных воздействий и их откликов по аналогии с линейными аналоговыми системами. Однако операции дискретизации и квантования сугубо нелинейные, тем более,  если эти операции являются достаточно «грубыми». Метод стохастической линеаризации,  устраняет эти противоречия, т. к. в нём реализуется операция аппроксимирующего усреднения.

Бинарными свойствами обладает операция «жесткого широкополосного ограничения – фильтрации», примененная в 70-х гг. Ю.Б. Черняком в радарах. Им же в работах [12, 13] доказаны линейные свойства такой обработки, что не является парадоксом, а скорее подтверждает существование некоторой закономерности, которую мы сегодня оформляем в новую теорию. Термины «стохастичность», «линеаризация», «обеление», «рандомизация» – почти синонимы, имеющие разные оттенки толкования в зависимости от решаемой задачи.

Статистическая теория обнаружения в классической формулировке при проверке гипотез оперирует вероятностями, которые являются первыми моментами  бинарной («грубой») статистики превышения порогов, которых в импульсной радиолокации может несколько:

- порог обнаружения единичного сигнала;

- порог обнаружения пачки;

- порог обнаружения траектории,

  и др.

Оператор математического  допускает применение случайных порогов и уравнивает ситуацию по достижимым вероятностям правильного обнаружения P_D и ложной тревоги P_F для «стохастического» и «нестохастического» случаев. Это подобие использовалось  в теории квантования распределений Шеппарда (поправки Шеппарда учитывают шум квантования распределений для стационарных процессов [14]).

Сказанное относится к блокам «стохастического оценивания» и имеющего с ним внешнюю связь – теорию оценок Фишера (теорию линейных оценок), которая оперирует моментами более высоких порядков, включая смешанные моменты и корреляцию. Однако, и в этом случае принцип подобия на основе равенства моментов непрерывных аналоговых процессов и их цифровых эквивалентов (в стохастическом случае) оставляет простор для поиска большого многообразия оригинальных инженерных решений по построению устройств оценивания, по существу являющихся цифровыми, но обладающими «аналоговыми» (Ю.Г.) свойствами.

Наконец, блок «стохастической фильтрации», который приобрел характеристику «стохастический» в основном за счет стохастического АЦП, однако в случае использования случайных весовых коэффициентов как в прямых, так и в обратных связях он действительно становится таковым. Получение структур стохастических цифровых фильтров принципиально было невозможным в ограниченных рамках классической теории линейных дискретных систем.

 

Условия решения задач обнаружения, оценивания и фильтрации

Обзор технических приложений рассматриваемой теории применительно к МР квантованию, вобуляции частоты повторения зондирующих импульсов, быстрой (поимпульсной) перестройки частоты в РЛС, стохастического обнаружения, стохастического квантования времени и пространства, стохастических измерителей параметров повторяющегося сигнала, многочастотной радиолокации приведён в [8].

Общий подход к оптимизации обнаружения и измерения параметров сигнала традиционен: для вектора наблюдения , сигнала цели  составляется отношение правдоподобия, после логарифмирования и упрощения для гипотез,  записывается оно в виде [6, 18]:

                        ,                                        (1)

 где  - корреляционная матрица гауссовой пассивной помехи (ПП)  с нулевым средним неизвестной мощности, * - знак комплексного сопряжения, η – порог.

Первое слагаемое в формуле (1) является отбеливающим режекторным фильтром (РФ), а второе - согласованным фильтром. Разность сравнивается с модифицированным порогом.

Известно, что согласованный фильтр максимизирует отношение в условиях равномерного шума, а отбеливающий фильтр декоррелирует цветной шум, делая его белым, при этом, порядок выполнения вышеупомянутых операций, может быть произвольным.

Величина есть отношение , увеличение которого способствует разделению функции плотности распределения вероятностей принимаемой сигнально-помеховой смеси для гипотез  и .

Аналогичные рассуждения можно сделать по отношению к АП. Однако, поскольку она коррелированна по пространству,  схема обработки для угла прихода АП формирует ноль характеристики пространственного фильтра. Далее осуществляется пространственная согласованная фильтрация, которая в целом максимизирует . Таким образом, система ПВ обработки формирует «нули» на оси доплеровских (для ПП) и пространственных (для АП) частот.

Пассивная помеха ПП демонстрирует двухкоординатную корреляцию по углу и времени (Доплеру), что сегодня оформлено построением современной теории ПВ обработки [6]. Эта теория легко развивается на случай N импульсов в пачке и MхL пространственных каналов по азимуту и углу места с использованием ПВ «окна наблюдений» размером NхMхL.

Пространственно-временные отличия сигналов цели и помех увеличивают соответствующие степени свободы взвешивания статистики наблюдения с помощью вектора пространственно-временных коэффициентов . Взвешивание отчетов с помощью этого вектора  осуществляется с целью реализации принципа согласованной фильтрации адаптивно в реальном времени.

Помехи от местных предметов коррелированны по пространству и времени, в то время как преднамеренная помеха коррелированна по углу и однозначно определена ситуационной задачей взаимного положения цели и постановщика помех.

ПВ обработка сигналов включает в себя  адаптивную настройку весовых коэффициентов , где N, M, L – номера временных и пространственных (по азимуту  и по углу места ) отсчетов, а N, M, L – размеры временного (N) и пространственного (M×L) окна, в попытке достичь максимального значения  и, следовательно, вероятности правильного обнаружения .

При этом используется понятие «сигнал/(помеха+шум приёмника+шум дискретизации и квантования)» , которое учитывает шумы квантования и (в более общем случае) другие эффекты дискретизации и квантования, присущие дискретной и цифровой обработке сигналов. Детализацию отношения  целесообразно проводить по Брэннану – Риду [4], но применяя рандомизацию обработки [8].

Процесс измерений параметров повторяющегося сигнала организовывается по принципу «удлиняющейся серии». В результате обзора методов введения рандомизирующих воздействий отмечена близость предлагаемого способа к «урновой схеме Пойя» и в меньшей степени сходство с классической процедурой Вальда, хотя последовательный (многоэтапный) анализ часто применяется [8].

Процесс оценивания может быть организован последовательно по серии (пачке) из N временных и М, L пространственных отсчетов в апертуре ФАР, в результате чего снижаются требования к разрядности квантователей и открываются возможности применения рандомизированной обработки всех координат. Размеры временных и пространственных окон по времени (N), азимуту (M) и углу места (L) выступают как естественный ресурс доплеровской и пространственной селекции.

На Рис. 3  - показана апертура антенны на плоскости ,  - вектор направления прихода электромагнитного излучения.

 

 

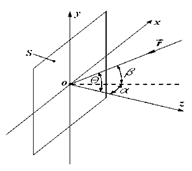
Рис. 3. Взаимосвязь угловых параметров прихода

 электромагнитной волны с   координатами апертуры ФАР

 

В рассматриваемом подходе пеленг цели q = q(a, b) для направления на источник излучения с азимута a и угла места b в течение выбранного времени обработки является практически постоянным.  В плоско-волновом приближении волна, падающая на апертуру ФАР под углом (пеленгом)  от оси антенны формирует поле, описываемое пространственными частотами:

                                 , ,                                     (2)

  где длина волны,  - пеленг, являющийся функцией азимута  и угла места  прихода электромагнитной волны.

Пространственная частота W  по аналогии с обычной («временной» Ю. Г.) частотой определяется как скорость изменения фазы, в данном случае по осям x, y. В отличие от обычной обработки сигналов во временной области, когда мы имели дело с частотой , здесь пространственные частоты ,  является функциями азимута  и угла места соответственно.

 Поскольку изменением пеленга за время пачки N импульсов, следующих с периодом Т, можно пренебречь, инструментальную погрешность измерения пеленга можно  уменьшать за счет рандомизированной обработки [8].

 «Обеление» ПП и АП помех осуществляется одновременно с «обелением» шумов квантования и использования конечной разрядности весовых коэффициентов (ВК) ЦФ и порогов квантования.

 Задача интерполяции дальности, скорости, азимута и угла места при использовании грубых текущих отсчётов соответствующих параметров сигналов – сводится к задаче  уточнения интерполирующей добавки  и связанной с ней вероятностью p=/Δ, где - ошибка квантования, подлежащая оценке; - шаг квантования [8]. Дальность D, пеленг , скорость цели V за время однократного контакта (пачке импульсов) являются практически являются постоянными величинами.

Таким образом, речь идет об измерении  методом статистических испытаний с использованием «грубой» (булевой) статистики , либо бинарно-знаковой статистики  Разумно введенная отрицательная корреляция между элементами всего вектора-выборки размером NxМxL может приводить к отрицательным членам с ковариациями в формуле для среднеквадратического ошибки (СКО) и уменьшить её по сравнению с обычным случаем.

Новизна предложения с позиции классической теории статистического обнаружения и оценивания состоит в том, что при оптимизации процедуры обработки номенклатура неинформативных параметров обрабатываемого сигнала искусственно расширяется.

Конкретизируем задачу обнаружения сигналов со случайными неинформативными параметрами, с учетом этого обобщения. Общий подход к синтезу оптимальных алгоритмов обнаружения сигналов, содержащих случайные неинформативные параметры, сформулируем для наиболее простой задачи оптимального обнаружения квазидетерминированного сигнала, когда неинформативные параметры случайны, а их законы распределения вероятностей известны. В этих случаях отношение правдоподобия, при каждом конкретном значении параметра рассматривается как условное, а безусловное отношение правдоподобия получается путем усреднения по случайным параметрам. В общем случае, пусть есть вектор неинформативных случайных параметров b^Т =(b₁,b₂,…,b_n) и  с известной совместной плотностью вероятностей w(b) = w(b₁, b₂,…, b_n).

Для получения отношение правдоподобия при наличии в сигнале неинформативных параметров, необходимо:

1) сформировать отношение правдоподобия в предположении, что эти параметры фиксированы и известны, т.е. ;

2) усреднить это условное отношение правдоподобия по случайным параметрам

                                                .

В литературе в классическом варианте [15-17] подробно рассмотрены случаи:

1 - случайная фаза, известная амплитуда (или эффективное значение) сигнала;

2- случайны, и фаза, и амплитуда (или эффективное значение) сигнала.

Предлагаемое обобщение связано с увеличением размерности вектора b^Т =(b₁,b₂,…,b_n)  с n до n + r с известной совместной плотностью вероятностей w(b) = w(b₁, b₂,…, b _{n + r}). Особенность решения данной задачи связана с реализацией возможностей использования «грубых статистик» (ГС или rough statistics RS) при соответствующей рандомизированной обработке RmDP - RS* в общем случае вновь вводимых r параметров у вектора неинформативных параметров b _{n +  r} , у которых закон распределения и параметры ПВ корреляция  задается Наблюдателем. Отметим, что  такой возможности при классической постановке задачи оптимального обнаружения не было, т.к. «стохастичность» в классической постановке была естественной и определялась заданными моделями отраженных сигналов, помех и собственного шума приёмника.

Для последующей интерпретации подхода в качестве базовой возьмём классическую теорию радиолокационного обнаружения сигналов, однако в ней учтём эффекты дискретизации и квантования. В терминологии Д. Миддлонта [19] уточним постановку задачи.

Задача приёма сигнала на фоне шума формулируется в рамках теории статистических решений. В общем случае сигнал подвергается ряду преобразований , где w – совокупность переданных, принятых сообщений или вытекающих из них решений;  - операция приёма, операция характеризующая влияние среды и операция передачи соответственно, N- размер временного окна, MxL – размеры пространственного окна в ФАР.

В классической теории решений проектировщик системы не может управлять сигналом на входе: операция передачи  задаётся априори, все сигналы заданы наперёд вместе с вероятностями наступления каждого из них, и проектировщик не может изменять эти данные, т. е. заданы распределения принимаемых сигналов F_N,M,L(/0) и F_N,M,L(/),где и  – N,M,L – мерные векторы пространства наблюдений и сигналов.

(Примечание. Обработку и формирование сигналов, в которой применяется рандомизация, назовем рандомизированной обработкой (randomized processing) и будем обозначать английской аббревиатурой RmP. Соответственно цифровую (digital) рандомизированную обработку будем обозначать RmDP – RS.)

Для этих случаев подробно исследуем совокупность технических приёмов обеления шумов квантования, что отражено введённым  понятия «рандомизация» (Р). В некоторых случаях будет применён термин линеаризация, полагая, что рандомизация обладает свойством линеаризации нелинейностей дискретизаторов, формирующих «грубые отсчеты». Термин randome (случайный) как уже говорилось предполагает искусственное введение случайностей (случайные пороги, случайные аддитивные учитываемые добавки, случайные весовые коэффициенты и др.) в процедуру обеления ПП, активных АП и шумов квантования, обусловленных дискретизацией по времени и пространству.

Предложенный метод как и метод Монте-Карло является инструментом, разрешающим компромисс между «дискретизацией», «грубым квантованием» и размерами окон ПВ выборок.

Сформулируем подкласс задач, который отличается тем, что в формировании пространства наблюдений принимает участие Наблюдатель, так что плотности вероятности выборки шума и смеси сигнала с шумом  и помехами задаются в виде

             F_N,M,L(/0, ) и F_N,M,L(/, ),                          (3)

где  – вектор рандомизирующего процесса параметров распределений, выбираемый Наблюдателем в пространстве параметров;

N, M, L – размеры окна временных (N) и пространственных (M, L) выборок.

Принадлежащие данному подклассу задачи названы задачами с варьируемыми случайными параметрами распределений, что показано на Рис. 4.

 

Рис. 4. Общая схема формирования пространства наблюдений:

а – классическая задача; б – задача с варьируемыми случайными параметрами.

В предлагаемом классе задач Наблюдатель получает дополнительную степень свободы помимо тех, которые имеются в задачах в классической постановке (назначение цен за ошибки при критерии среднего риска или назначение вероятности ложной тревоги при критерии Неймана-Пирсона).

Таким образом, отыскивается оптимальная операция приёма (обработки) данных для поставленного класса задач. Обозначим эту операцию по аналогии с операцией  как . Поскольку операция  по определению является оптимальной, она должна переходить в операцию , когда наблюдателем выбран вектор параметров , т. е.  когда распределения (3) переходят в исходные распределения и тем самым однозначно (в статистическом смысле) определяется пространство наблюдений,

,                                 (4)

где  - операция выбора (select) оптимального вектора .

Таким образом, нахождение  сводится к отысканию операции . На сегодня в целом задача не решена, однако при решении конкретных задач в работе найдено множество частных решений. В [8] описан целый ряд конкретных устройств, реализирующих различные способы обеления («рандомизации», «стохастической линеаризации», «накачки», «вобуляции» и т.п), процедуры устранения (уменьшения) эффектов дискретизации и квантования, в т.ч. за счёт использования стохастических шкал квантования времени и пространства  [20] (см. Рис. 5).

Использование таких шкал ценой некоторых энергетических потерь (эквивалентных наложению окон) позволяет уменьшить (сгладить) боковые лепестки функций отсчётов, а следовательно и АЧХ ЦФ.

Поведение «хвостовой» части функции соответствует асимптотическому, менее пульсирующему, уменьшению боковых лепестков.

 В [20] оценена точность восстановления исходных зависимостей. Случайная шкала дискретизации при  слабо влияет на восстановление сигналов низких частот и констант.

 

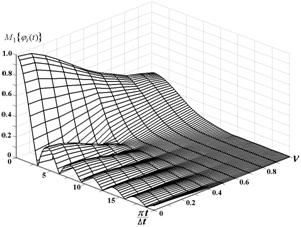
Рис. 5. Трехмерное изображение усредненной функции отсчетов .

При стохастической дискретизации установлено, что функции отсчетов   могут быть случайными, так как это не противоречит условию независимости  (ортогональности), по крайней мере, для эргодических процессов. Это означает, что коэффициенты разложения  могут быть случайными и добавятся шумы в реконструируемый сигнал. Придание «стохастичности» дискретизации, например, за счет введения случайной шкалы , где - случайная величина с нулевым средним и дисперсией ,  - среднеквадратическое отклонение , позволило задействовать резервы усреднения, связанные с удлинением и повторяемостью ПВ выборок.

Анализ поведения функции отсчётов (см. рис.5) показал, что при увеличении индекса вобуляции  шкалы квантования имеются некоторые энергетические потери, расширяется главный лепесток, но существенно (с 13 до 26 дБ) уменьшается первый боковой лепесток, что позволило (см. [20]) сделать выводы об аналогии воздействия стохастических шкал квантования с использованием известных окон Хемминга, Ханна и др. При дозированном введении «стохастичности» при уменьшенном  возможно получение «суммарного» эффекта окон и шкал квантования.

Ключевая парадигма теории стохастической радиолокации базируется на концепции внедрения в процесс обработки и формирования радиолокационных сигналов искусственной стохастичности, предполагающих  наряду с естественной стохастичностью, обусловленной случайной природой входных сигналов,  рандомизацию условий  процесса «приём – передача».

 

Применение и перспективы

Анализ общих сведений об обработке сигналов в радиолокации в явном виде не дает ответа на вопрос: какой должна быть обработка сигналов: аналоговой или цифровой? Установлено одно, что статистика обрабатываемых сигналов в угоду технических ограничений может быть достаточно «грубой» при рандомизации.

Технические приложения  исследуемых методов рандомизированной обработки и формирования сигналов группируются вокруг решения следующих вопросов:

- устранения или уменьшения влияния стробоскопических эффектов по оси доплеровских и пространственных частот (угловых направлений);

- уменьшения или усреднения боковых лепестков частотных характеристик (ЧХ) ЦФ, диаграмм направленности (ДН) антенн ФАР и улучшения пространственно-частотных характеристик ЦФ ПВ обработки сигналов;

- изменения условий сложения векторов ЭМИ в дальней зоне с целью диаграммо-образования, устранения или уменьшения провалов в ЭПР диаграммы вторичного излучения целей при последовательной обработке;

- стабилизации вероятности ложных тревог (ВЛТ) за счет использования  технологии RmDP - RS;

- снижения разрядности текущих РЛ данных – вплоть до использования простых монобитовых грубых RS статистик: «булевых» и «бинарно-знаковых».

 

Заключение

Анализ основ теории оптимального обнаружения и измерения показывает, что путем введения понятия рандомизированной обработки грубых RS статистик и разработки  вытекающей из неё технологии RmDP – RS стохастическая радиолокация естественным образом встраивается классическую теорию и дополняет её.

Обобщение проведенных предварительных исследований по выбранному направлению стохастической радиолокации показывает, что имеются резервы повышения эффективности ЦО ПВ сигналов, её основных процедур (обнаружения, оценивания параметров, фильтрации по обычным и пространственным частотам - угловым направлениям в условиях ограничений на ресурсы ЦО (разрядность входных данных, разрядность АЦП, размеры окон ПВ выборок, частоты дискретизации и квантования) путем рандомизации «грубых» отсчётов (ГО) с бинарными свойствами (малоразрядных, бинарно-знаковых, булевых и т. п.)., которые могут быть использованы в  разработках бортовых РЛС нового поколения.

 

Литература

1. Горбунов Ю.Н. Повышение эффективности обработки и формирования сигналов в РЛС с СДЦ методами рандомизации.// Труды 7 МНТК «Радиолокация и радиосвязь», г.Москва, 26-30 ноября 2013 г.

2. Лихарев В.А. Цифровые методы и устройства в радиолокации. - М.: Советское радио, 1973.- 456 с.

3. Слока В.К. Вопросы обработки радиолокационных сигналов. - М.: Советское радио, 1970. – 256 с.

4. Brennan L. E., Reed I. S. Quantization Noise in digital Moving Targets Indication Systems. // IEEE Transaction, 1966, vol. AES-2, №6. - р. 655-658.

5. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию:

 Пер. с англ. М.: Радио и связь, 1986. – 448 с., ил.

6. R. Klemm. Space-Time Detection Theory // The material in this publication was assembled to support a lecture series under the sponsorship of the sensor and lectronicsTechnology Panel (SET) and the Consultant and Exchange Programmer of RTO presented on 23-24 september 2002 in Moscow, Russia.

7.  Воскресенский Д.И. Антенны с обработкой сигнала: Учеб. Пособие для вузов.  М.: САЙНС – ПРЕСС, 2002. – 80 с.: ил.

8. Горбунов Ю.Н. Цифровая обработка радиолокационных сигналов в условиях использования грубого (малоразрядного) квантования. Монография. М.: ФКА, ФГУП «ЦНИРТИ им. акад. А. И. Берга», 2008. – 87 с., (http://www.cnirti.ru/pdf/d_260109.doc).

9.  Горбунов Ю.Н., Бондарев А.В. Алгоритмы и устройства цифровой стохастической обработки сигналов в радиолокации.: Монография - Учебное пособие. - М.: НИЦЭВТ, ИПК МРП, 1990. - 144 с.

10. Горбунов Ю.Н. Цифровые стохастические радары: принятие решений, стохастическое обеление помех, рандомизация измерений параметров, применение. // Труды VIII международной научно-технической конференции «Кибернетика и высокие технологии XXI века». – Воронеж: НПФ «Саквоее», 2007, т.I.-С. 446-455.

11.  Томас. Непараметрические методы обнаружения сигналов.// ТИИЭР. - 1970. - т. 58. - №5. – с. 23 – 31.

12. Черняк Ю. Б. Корреляторы с идеальными ограничителями // Радиотехника. – 1965. - т.20. - №3.

13. Черняк Ю. Б. Об эффективности квантования при цифровой фильтрации сигналов в коррелированном шуме // Вопросы радиоэлектроники. – 1980.- Серия От. - Выпуск 1.

14. Корн Г. А. Моделирование случайных процессов на аналого-цифровых машинах. - М.: Мир, 1968. - 315 с.

15. Теоретические основы радиолокации. Под ред. Ширмана Я.Д. Учебное пособие для вузов. – М.: Советское радио. – 1970. – 560 с.

16. Теоретические основы радиолокации. Под ред. Дулевича В.Е. Учебное пособие для вузов. – М.: Советское радио. – 1978. – 608 с.

17. Черняк В.С. Конспект лекций «Радиотехнические системы», - МАИ, - 2010 г.

18. Горбунов Ю. Н. Цифровые системы СДЦ и их оптимизация: Монография // МГТУ МИРЭА.- М., 2008. – 132 с. (http://www.cnirti.ru/pdf/d_260109.doc

19. Миддлтон Д. Введение в статистическую теорию связи. // В 2-х томах. – Т. 1,2.

Пер.с англ. под ред. Б.Р. Левина. – М., «Сов. Радио» , 1961, 1962.

20. Горбунов Ю.Н. Стохастическое временное и пространственное квантование в плоских апертурах фазированных антенных решеток. // Труды X Международной научно-технической конференции «Радиолокация, радионавигация и связь». – Воронеж: Изд. НПФ «Саквоее», 2005, т. III. - с. 1790 - 1798.