Разработка конструкций ДИЭЛЕКТРИЧЕСКИХ купольных линзовых антенн СВЧ диапазона с улучшенными аэродинамичскими характеристиками и повышенной механической прочностью

 

Ю. В. Медведев
ФГБУ «16 Центральный научно исследовательский испытательный институт» Минобороны России

Статья получена 30 сентября 2014 г.

Аннотация. Приведены конструкции диэлектрических купольных линзовых антенн (КЛА), определены области их применения. Проведено численное исследование энергетических, аэродинамических и прочностных параметров диэлектрических купольных линзовых антенн (КЛА) с учетом массы линзы. Получены зависимости коэффициента усиления и коэффициента аэродинамического сопротивления от геометрических параметров КЛА летноподъемного средства (ЛПС), осуществляющего полет на высоте 8 км над уровнем моря со скоростью 400 км/ч. Показана возможность снижения коэффициента аэродинамического сопротивления антенны путем уменьшения геометрических размеров купольной линзы при сохранении значения коэффициента усиления. Получены зависимости коэффициента усиления и коэффициента запаса прочности по критерию Мизеса от геометрических параметров КЛА. Показана возможность увеличения коэффициента запаса прочности антенны путем уменьшения геометрических размеров купольной линзы с сохранением значения коэффициента усиления. Получены зависимости массы линзы от изменения ее габаритных размеров. Показана возможность снижения массы линзы при рациональном выборе ее геометрических размеров.

Ключевые слова: диэлектрические купольные линзовые антенны, купольная линза, широкоугольное электрическое сканирование, сектор сканирования, фазированная антенная решетка, коэффициент аэродинамического сопротивления, коэффициент запаса прочности, коэффициент усиления антенны.

Abstract. Designs of dielectric dome lens antennas are presented, areas of their application are defined. The numerical research of the aerodynamic and energy parameters of the dome lens antennas on the aircraft is carried out. The dependencies of the aerodynamic drag coefficient and antenna gain for the geometric dimensions of the lens of the antenna on the aircraft, which accomplishes flight at the height of 8 km above sea level at a rate of 400km/h are obtained. The possibility of reduction in the aerodynamic drag coefficient of antenna by decreasing the geometric dimensions of dome lens with the retention of the value of the antenna gain is shown. The numerical research of the antenna gain and factor of safety for max von Mises criterion is carried out. The possibility of increasing more than 2 times the factor of safety by changing geometric parameters of the lens in the range of 20% on the baseline values, and also their rational selection with the value retention of the required antenna gain is shown.

Keywords: dielectric dome lens antennas, dome lens, wide angle electrical scanning, scanning area, phased antenna array, aerodynamic drag coefficient, coefficient of safety factor, antenna gain.

 

 

В настоящее время в связи с освоением более высокочастотной части СВЧ диапазона, а также в связи с расширяющимся кругом задач по обеспечению связи в сложной электромагнитной обстановке, требования к антеннам ужесточаются. Антенны могут размещаться как на стационарных, так и на подвижных объектах. Для поддержания требуемых энергетических потенциалов радиолиний антенны должны обладать достаточно высоким коэффициентом усиления (КУ) и, следовательно, формировать узкие, игольчатые диаграммы направленности (ДН) с возможностью образования нулей ДН в направлении помех, и обеспечивать высокоскоростное одно- или многолучевое сканирование в полусферическом пространстве, отслеживая положение подвижных объектов с учетом колебаний транспортной базы.

 

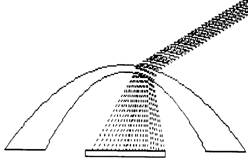
Рис. 1. Купольная линзовая антенна.

Рис. 2. Линза с зонированным профилем.

 

Одним из возможных и наиболее перспективных путей решения задач по обеспечению связи с подвижными и стационарными объектами в СВЧ диапазоне является использование диэлектрических купольных линзовых антенн с высокоскоростным широкоугольным электрическим сканированием. КЛА содержат купольную диэлектрическую рассеивающую линзу и плоскую фазированную антенную решетку (ФАР), расположенную в ее основании (см. рис. 1) [1,2]. На рис. 1 представлены траектории лучей в угломестном сечении варианта конструкции КЛА, построенные в приближении геометрической оптики для угла сканирования q = 60° и относительной диэлектрической проницаемости материала линзы e = 38. Рассеивающий геометрический профиль образован из отрезков парабол. Снижение массы линзы может быть достигнуто путем зонирования геометрического профиля линзы. На рис. 2 представлен вариант зонированного рассеивающего профиля линзы, образованного из отрезков окружностей. Рассеивающий геометрический профиль линзы КЛА может иметь различную форму, в частности, может быть образован из отрезков парабол, окружностей, гипербол, эллипсов, и др., а также их сочетаний.

Как показывают исследования [3], в настоящее время возможно создание КЛА различных конструкций с высокоскоростным электрическим сканированием в широком секторе углов: 360° по азимуту и 0° ... 118° по углу места. Имея расширенный сектор и высокую скорость сканирования, а также обеспечивая управление формой ДН и ее положением в пространстве, КЛА могут найти свое применение в средствах радио, радиорелейной и спутниковой связи стационарных и мобильных объектов.

Поскольку купольная линза выполняет роль не только преломляющей призмы, но и защищает антенную решетку от внешних воздействий, в основном линза и будет определять прочность конструкции антенны, а также ее аэродинамические характеристики. Энергетические, аэродинамические и прочностные характеристики КЛА являются величинами, зависимыми от геометрических параметров линзы.

Для оценки аэродинамических и энергетических характеристик КЛА проведено исследование зависимости коэффициента аэродинамического сопротивления и КУ антенны от геометрических размеров купольной линзы при условии крепления антенны к обшивке ЛПС, осуществляющего полет на высоте 8 км над уровнем моря со скоростью 400 км/ч.

Исследование проводилось численными методами [4]. Расчет коэффициента аэродинамического сопротивления антенны под действием аэродинамической нагрузки осуществлялся с использованием твердотельной модели антенны, выполненной в натуральную величину, при этом крепление антенны к обшивке ЛПС смоделировано ее размещением на полубесконечной плоскости, размеры которой много больше размеров антенны. Для расчета коэффициента усиления антенны использовалась математическая модель КЛА, построенная в приближении геометрической оптики и приближении Кирхгофа [5]. При расчетах считалось, что линза имеет идеально гладкую поверхность. Исходные параметры линзы соответствовали следующим параметрам: D₀/D_AP = 3,0; D/D_AP = 2,0; H/D_AP = 1,0; h/D_AP = 0,9165, относительный диаметр антенной решетки D_AP/λ = 40, где λ = 8 мм длина волны в свободном пространстве (см. рис. 3).

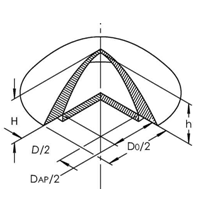
Рис. 3. Параметры КЛА.

Для нахождения коэффициента аэродинамического сопротивления Cx (коэффициента обтекаемости) использовано соотношение [6]:

                                                            (1)

где f – сила аэродинамического (лобового) сопротивления; р – плотность воздуха; v – скорость относительного движения воздуха и антенны; s – площадь наибольшего поперечного сечения антенны (лобовая площадь). Необходимые для расчетов значения плотности воздуха ρ = 0,49 кг/м³, давления p = 33031,95 Па и температуры t = −40° C на высоте H = 8км над уровня моря выбраны из справочника [7]. Проведено исследование изменения коэффициента усиления G для угла сканирования антенны 0° и коэффициента аэродинамического сопротивления антенны C_x при изменении высоты H и внешнего диаметра основания линзы D₀ в сравнении с исходными значениями в условиях воздействия на антенну движущегося со скоростью 400 км/ч воздушного потока, направленного под углом 90° к оси симметрии антенны. В ходе исследования получено продольное сечение диаграммы движения воздушного потока вдоль поверхности линзы (рис. 4). Темные области диаграммы указывают на пониженное давление, образующееся за счет слабого обтекания воздушным потоком мест крепления основания линзы к поверхности, светлая о повышенном давлении у поверхности линзы и высокой скорости ее огибания воздушным потоком. Стрелками указано направление движения вектора скорости воздушного потока. Как видно из диаграммы, наибольшее давление испытывает область при вершине линзы, а за линзой в ее основании существует значительная область высокого разряжения. Результаты исследования приведены на рис. 5 в виде графиков, отражающих изменение коэффициентов усиления и аэродинамического сопротивления антенны. Изменение параметров линзы задано в процентах относительно исходных значений. При проведении расчетов изменялся только один параметр, а остальные сохранялись равными своим исходным значениям.

 

Рис. 4. Движение воздушного потока вдоль поверхности линзы.

 

 

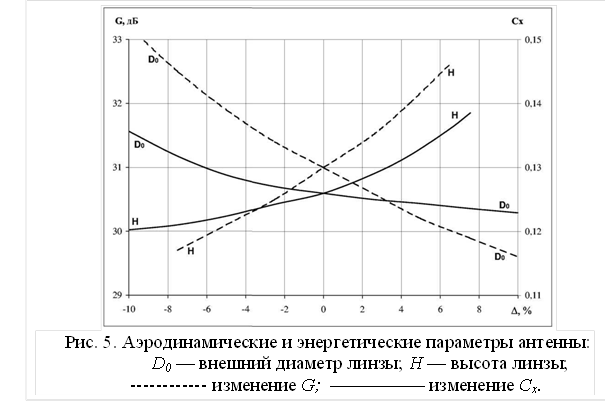
Как следует из полученных результатов, аэродинамическое сопротивление антенны снижается с уменьшением высоты и с увеличением внешнего диаметра линзы. Аналогичная зависимость наблюдается и для КУ антенны, который повышается при увеличении высоты и уменьшении внешнего диаметра линзы. Наиболее эффективно аэродинамическое сопротивление снижается за счет уменьшения высоты линзы. Точки пересечения графиков C_x для H и D₀ и графиков G для H и D₀ в данном случае можно считать исходными точками выбора рациональных значений высоты и внешнего диаметра основания линзы при заданных значениях C_x и G, соответственно. Так, при снижении высоты линзы на 2% относительно исходного значения (КУ снизится на 0,4 дБ) для поддержания требуемого усиления антенны (31 дБ) необходимо уменьшить внешний диаметр основания линзы на 2,5% относительно исходного значения, что даст увеличение КУ до требуемой величины, т.е. на 0,4 дБ. При этом снижение высоты линзы приведет к снижению коэффициента аэродинамического сопротивления антенны на 0,01, а увеличение диаметра внешнего основания к увеличению C_x на 0,01, что даст исходное значение C_x = 0,126. Изменения высоты и внешнего диаметра основания линзы на 10% относительно исходных значений дают незначительные, на единицы сотых долей изменения коэффициента аэродинамического сопротивления антенны, свидетельствующие о том, что линза имеет хорошо обтекаемую форму. Абсолютное значение коэффициента аэродинамического сопротивления C_x = 0,126, полученное при исходных геометрических размерах линзы, говорит о хорошей аэродинамичности антенны. На основании полученных зависимостей C_x и G возможно осуществить выбор рациональных геометрических размеров линзы при заданных значениях коэффициентов усиления и аэродинамического сопротивления антенны.

Для оценки прочностных характеристик КЛА проведено аналогичное исследование изменения коэффициента усиления G для угла сканирования антенны 0° относительно направления в зенит и коэффициента запаса прочности линзы η при изменении внешней H и внутренней h высоты, внешнего D₀ и внутреннего D диаметра основания линзы в сравнении с исходными значениями. Расчет напряженно деформированного состояния линзы и оценка прочности КЛА выполнялась по критерию Мизеса (von Mises - критерий энергии формоизменения), определяющего момент исчерпания несущей способности сравнением величины эквивалентного напряжения с пределом текучести материала. Эквивалентные напряжения σ_υonMizes в точках дискретизации объема тела рассчитывались по формуле:

 

(2)

 

где σ1, σ2, σ3 – главные напряжения, эквивалентное напряжение не зависит от ориентации площадки, на которой оно действует, то есть является инвариантным, а коэффициент запаса прочности η  вычислялся как отношение величины прочности (предела текучести, предела прочности, другой величины) к максимальному, в пределах детали, эквивалентному напряжению. В качестве материала линзы для проведения исследования выбран высокочастоный диэлектрик Morgan Advanced Ceramics DeranoxT^M 970 плотностью 3,74 г/см², содержащий 97,0% высококачественного оксида аллюминия Al₂O₃, имеющий предел прочности на сжатие 2000 МПа, диэлектрическую проницаемость ε = 9,1 и тангенс угла диэлектрических потерь tgδ = 6,7 ∙ 10^-4. Исходные параметры линзы соответствовали следующим значениям: D₀/D_AP = 3,0; D/D_AP = 2,0; H/D_AP = 1,0; h/D_AP = 0,9165, относительный диаметр антенной решетки D_AP/λ = 40, где λ = 6,74 мм – длина волны в свободном пространстве (см. рис. 3).

Рис. 6. Расчет прочности купольной линзы

Результаты расчета прочности линзы приведены на рис. 6, где показано сечение линзы с распределением коэффициента запаса прочности, полученном в ходе расчета напряженно деформированного состояния линзы при условии равномерно распределенного давления, порядка 100 кПа по ее поверхности, направленного сверху вниз перпендикулярно плоскости основания.

Как видно из рисунка, возникающие напряжения, а также коэффициент запаса прочности распределяется по объему линзы неравномерно. В линзе имеются две области с наибольшим напряжением, соответствующие минимальным значениям коэффициента запаса прочности (отмечены темным цветом). Эти области располагаются у основания линзы, поскольку оно имеет жесткую фиксацию, вызывая повышенное напряжение у мест крепления с внутренней стороны, и у вершины линзы, т. к. в этом месте линза имеет минимальную толщину. Светлыми тонами на рисунке показаны области наименьшего напряжения с максимальным коэффициентом запаса прочности. Поскольку наибольшие деформации возникают в линзе у ее вершины, там, где она имеет наименьшую толщину, в дальнейшем при проведении исследования значения коэффициента запаса прочности рассматриваются именно в этой точке.

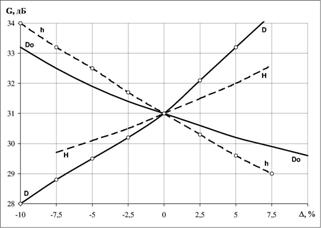
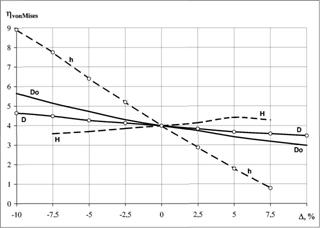
Результаты исследования приведены на рис. 7 и 8 в виде графиков, отражающих изменение коэффициента усиления антенны G и коэффициента запаса прочности линзы η. На графиках, кривые, обозначенные литерой D_o, показывают зависимость исследуемых параметров от изменения внешнего диаметра основания линзы, литерой D - от изменения внутрен­него диаметра основания линзы (изменение толщины линзы у основания), литерой Н - от изменения внешней высоты линзы, литерой h - от изменения внутренней высоты линзы (изменение толщины линзы у вершины). Вдоль вертикальной оси рис. 7 отложены значения усиления антенны в дБ, вертикальная ось рис. 8 отображает безразмерный коэффициент запаса прочности линзы, горизонтальные оси обеих рисунков показывают изменения размеров линзы в процентах. Изменение параметров линзы задано в процентах относительно исходных значений. При проведении расчетов изменялся только один параметр, а остальные сохранялись равными своим исходным значениям.

 

Рис. 7. КУ КЛА.

Рис. 8. Коэффициент запаса прочности.

 

Как видно из результатов исследования, наибольшее влияние на прочность линзы оказывает изменение толщины линзы у вершины. Изменение внутренней высоты линзы на 17,5% приводит к изменению коэффициента запаса прочности более чем в 8,5 раз. При толщине линзы у вершины 4 мм и давлении 100 кПа запас прочности составляет 0,79, что приведет к разрушению конструкции при данной нагрузке. Повысить прочность линзы в 1,5 раза возможно путем уменьшения внешнего диаметра линзы и путем увеличения толщины линзы у ее основания в пределах 20% от исходных значений. Наименьшее влияние на изменение прочности линзы оказывает изменение высоты линзы. Так, увеличение высоты линзы на 15% позволя­ет повысить коэффициент запаса прочности с 3,58 до 4,28. В целом конструкция линзы с исходными размерами позволяет выдерживать нагрузки в пределах 1,02кгс/см² при четырехкратном запасе прочности.

КУ антенны (см. рис. 7) растет при увеличении внешней высоты линзы и толщины линзы при вершине, а также при уменьшении внешнего диаметра линзы и уменьшении толщины линзы при основании. Точки пересечения графиков G и η, соответствующие исходным геометрическим параметрам линзы, являются исходными точками выбора рациональных внешней и внутренней высоты, внешнего и внутреннего диаметра основания линзы при заданных значениях коэффициента запаса прочности η и коэффициента усиления G антенны.

Так, например, при необходимости уменьшения габаритов антенны на 5%, снижение высоты линзы на эту величину приведет к снижению КУ антенны относительно исходного значения на 0,9 дБ, а уменьшение внешнего диаметра линзы на 5% позволит компенсировать полученный при уменьшении высоты недостаток усиления. При этом уменьшение внешней высоты приведет к снижению коэффициента запаса прочности линзы с 4 до 3,7 (относительно исходного значения), однако уменьшение внешнего диаметра линзы дает возможность повысить прочность линзы на 0,7 единицы, что в итоге позволит увеличить прочность линзы относительно исходного значения на 0,4 единицы. На основании полученных зависимостей η и G возможно осуществить выбор рациональных геометрических размеров линзы при заданных значениях коэффициента усиления и коэффициента запаса прочности антенны.

Для оценки возможности выбора рациональных массогабаритных показателей конструкции антенны проведено исследование зависимости массы линзы от изменения ее габаритных размеров. Результаты расчета зависимости массы линзы от ее геометрических размеров приведены на рис. 9 в виде графика, вертикальная ось которого показывает значения массы, а горизонтальная изменение размеров линзы в процентах.

 

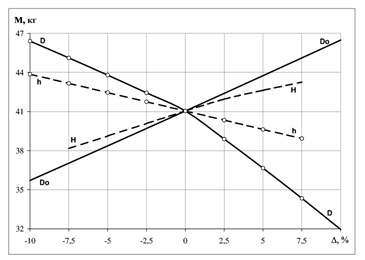
Рис. 9. Масса линзы КЛА

Как видно из рисунка, изменение размеров линзы на ±10% относительно исходных значений приводит к значительному изменению массы линзы, более чем на ± 5 кг при исходной массе линзы 41 кг. Наибольшего снижения массы линзы можно добиться путем уменьшения ее толщины у основания. Также снизить массу линзы возможно путем уменьшения высоты линзы, уменьшения ее внешнего диаметра и уменьшения ее толщины при вершине.

Таким образом, при разработке диэлектрических КЛА, в частности и для мобильных объектов, необходимо учитывать прочностные, аэродинамические показатели и массу антенны, которые могут быть улучшены путем изменения геометрических параметров линзы без ухудшения энергетических показателей антенны. Проведенные численные исследования изменения коэффициента запаса прочности, коэффициента аэродинамического сопротивления, массы линзы и КУ в зависимости от изменения размеров купольной линзы показали, что путем изменения геометрических параметров линзы в пределах 20% относительно исходных значений, а также их рационального выбора, возможно добиться снижения массы линзы более чем на 10 кг, более чем в 2 раза повысить прочность конструкции и в 1,25 раза снизить коэффициент аэродинамического сопротивления антенны с сохранением требуемого усиления в секторе сканирования.

 

Литература

1.     Stangel J., Valentino P. − Canadian patent, no.977844, cl.333-17.43, cl.333-17.35, 1975.

2.     Медведев Ю.В., Харланов Ю.Я. и др. − Патент RU №2201021 C2, кл. H 01 Q 15/08, приор. 04.09.2000, опубл. 20.03.2003, бюл. № 8.

3.     Медведев Ю.В., Харланов Ю.Я. Характеристики купольных линзовых антенн, используемых в мобильных средствах спутниковой и радиорелейной связи в движении диапазонов ММВ и СМВ // Антенны.—М.,2004.— Вып. 2(81).— С. 20 — 25.

4.     Алямовский А.А., Собачкин А.А., Одинцов Е.В., Харитонович А.И., Пономарев Н. Б. Solid Works. Компьютерное моделирование в инженерной практике.— СПб.: «БХВ   Петербург», 2006.— 800 с.

5.     Кашин С.В.   Расчет   линз   из   однородного   диэлектрика//Радиотехника.— 1990.— №1.— С. 87.

6.     Кан С.Н., Свердлов И.А. Расчет самолета на прочность: Учебник для вузов по расчету самолета на прочность.— Изд. 5-е, перераб. и доп. М.: «Машиностроение», 1966.— 520 с.

7.     HUTTEЁ. Справочная книга для инженеров, архитекторов, механиков и студентов // Перевод с 25-го немецкого издания под общей редакцией Московского Механического Института имени М.В. Ломоносова. Т. 1.— Изд. 13-е, испр. и доп.— М.: «Главлит», 1930.— С. 362.