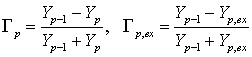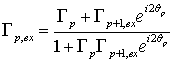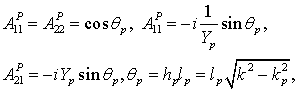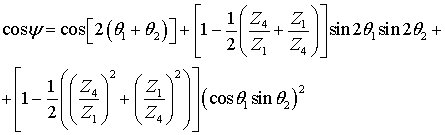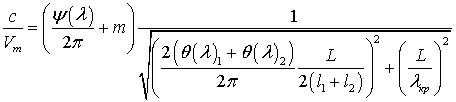ИССЛЕДОВАНИЕ ДИСПЕРСИИ В ЗАМЕДЛЯЮЩИХ СИСТЕМАХ ТИПА ЦЕПОЧЕК СВЯЗАННЫХ РЕЗОНАТОРОВ С РАЗНЫМИ ЩЕЛЯМИ СВЯЗИ

 

В. А. Солнцев, И. С. Омельчук

Московский институт электроники и математики Национального исследовательского университета «Высшая школа экономики»

 

Статья поступила в редакцию 15 октября 2015 г.

 

Аннотация. Исследованы свойства петляющих замедляющих систем (ЗС) типа цепочек связанных резонаторов (ЦСР) с разными щелями связи. Показана   возможность работы таких ЗС во второй полосе пропускания и увеличения рабочей частоты ЛБВ при сохранении размеров ЗС.

Ключевые слова: СВЧ, дисперсия, замедляющие системы, лампа бегущей волны, волноводно-резонаторная модель.

Abstract. The properties of slow-wave system (SWS) type of coupled cavity system with different slots connection are studied. The possibility of such SWS in the second bandwidth and increase of the operating frequency of the TWT, while maintaining the size of the SWS are shown.

Keywords: microwave, dispersion, slow-wave systems, traveling-wave tube, waveguide resonator model.

 

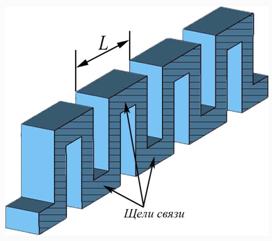
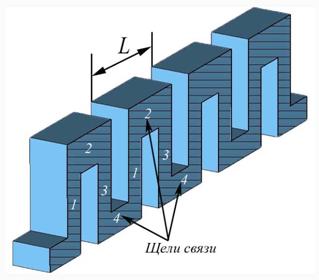
В мощных лампах бегущей волны (ЛБВ) широко применяются замедляющие системы (ЗС) типа цепочек связанных резонаторов (ЦСР) и подобные им ЗС с петляющим потоком энергии, например встречные штыри. В типичной ЗС ЦСР, схема которой приведена на рис. 1, соседние щели связи одинаковые и повернуты на , так что поток энергии также поворачивается на . В таких ЗС рабочей является первая пространственная гармоника электромагнитного поля в основной полосе пропускания ЗС. 

В настоящей работе рассматриваются свойства петляющих ЗС типа ЦСР  с разными щелями связи, в том числе  возможности работы таких ЗС во второй полосе пропускания и увеличения рабочей частоты ЛБВ.

 

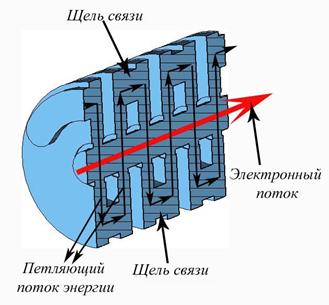
Рис. 1 Схема ЗС ЦСР с одинаковыми щелями связи.

Электродинамические свойства петляющей ЗС в одномодовом приближении можно описать волноводно-резонаторной моделью (ВРМ) [1], представляющей цепочку последовательно  включенных  «звеньев» цепочки – отрезков волноводов, резонаторов, щелей связи и др.(рис.2).

 

Рис. 2.Волноводно-резонаторная модель петляющей ЗС с одинаковыми щелями связи

 Аналогично в слоистой среде каждый слой можно рассматривать как отдельное звено (элемент)цепочки. В  обоих случаях структуру можно представить цепочкой четырехполюсников с  подключенными входной   и выходной  проводимостями нагрузки (рис. 3).

В общем случае четырехполюсники не идентичны, а их число Р не совпадает с числом зазоров взаимодействия Q в ЗС. Фильтровые свойства, полосы пропускания и запирания системы описываются частотной зависимостью входного коэффициента отражения .

 Для вычисления коэффициента отражения можно использовать стандартные процедуры перемножения матриц передачи  или известные программы вычисления матриц рассеяния электродинамических систем.

 

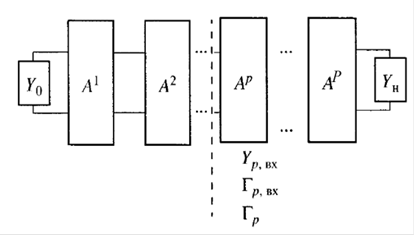
Рис. 3. Модель ЗС и слоистой среды в виде цепочки четырёхполюсников.

 

Используем более простой способ вычисления  , следуя [2], введем локальный  и полный   коэффициенты отражения на входе p-го четырехполюсника:

,                                                          (1)

 

где  ,  - волновая и входная проводимость p-го четырехполюсника соответственно.

 Будем считать четырехполюсники, соответствующие отдельным элементам, горизонтально симметричными. Коэффициенты их матрицы передачи , обладают следующими свойствами: , , а волновая проводимость  и набег фазы  определяются соотношениями , , .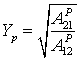

Входящий в цепочку p-й четырехполюсник имеет нагрузку  , и, следовательно, его входная проводимость   определяется рекуррентным выражением

, .              (2)

Оно позволяет определить входную проводимость через проводимость нагрузки   в конце цепочки. Из выражений для ,  и  получаем рекуррентные соотношения для коэффициента отражения

.                                                                         (3)

 Значения входящих в них фаз и локальных коэффициентов отражения  определяются структурой конкретных вариантов систем. В частности, в ВРМ в качестве отдельных элементов берутся отрезки волноводов с длинами , фазовыми постоянными  и эквивалентными волновыми проводимостями . Элементы матрицы передачи для них имеют вид:

                                                   (4)

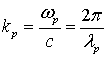где  – волновое число в свободном пространстве,  - критическое волновое число и критическая длина волны  рассматриваемой моды p-го отрезка волновода. Каждый элемент описывается двумя параметрами - волновой проводимостью  и электрической длиной .  Такое описание справедливо не только для отрезков волноводов, но и для элементов другого вида, описываемых симметричными четырехполюсниками. Отличаются только их зависимости проводимости  и фазы  от частоты. В частности, для длинных линий , для слоистой среды с разными диэлектрическими проницаемостями  и толщинами слоёв   имеем: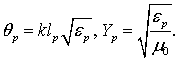

 

Простейшей ВРМ для петляющей ЗС является четырехэлементная периодическая структура из  4-х отрезков волноводов на периоде (рис. 2), позволяющая описать основные свойства ряда ЗС в низших полосах пропускания.

Рассмотрим  ВРМ  из четырёх отрезков волноводов (рис. 2) при учете в каждом из них только одной волны с волновым числом и волновым сопротивлением.

Для прямоугольного волновода это волна типа  с компонентами электрического поля

        (5)

где 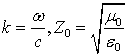– волновое число и импеданс в свободном пространстве,

 – критическое волновое число волны  волновода,

 

оси x, y, z направлены соответственно вдоль широкой стенки размером «a», узкой стенки размером «b» и продольной оси рассматриваемого отрезка волновода. В общем случае для составления ВРМ можно использовать отрезки волноводов любого сечения.

Такая ВРМ приближенно описывает основные свойства ЗС, по крайней мере, в первых двух полосах прозрачности и непрозрачности для ЗС петляющего типа (петляющий волновод, встречные штыри, цепочка связанных резонаторов со щелями связи, повернутыми на 180°), а также для спирального скрученного волновода.

 

Рис. 4. Волноводно-резонаторная модель петляющей ЗС с разными щелями связи

Используем определение волнового сопротивления прямоугольного волновода Z как отношение среднего по x напряжения U к поверхностному току J вдоль оси волновода [4]:

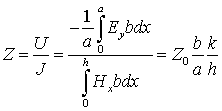                                                                     (6)

Тогда элементы матрицы передачи j-го отрезка волново­да геометрической длины  и электрической дли­ны  имеют вид (4), а матрица передачи на одном периоде ЗС (см. рис. 2) получается как произведение четырех матриц .  Уравнение дисперсии имеет вид , где фазовый сдвиг на период. Замедление m-ой пространственной гармоники волны ЗС связано с фазовым сдвигом соотношением:

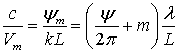                                                                         (7)

Рассмотрим два случая.  Возьмем сначала  систему, у которой , а набеги фаз на каждом отрезке будем брать из учета: . Это система с разными щелями связи (отрезки 2 и 4, рис.4), причем соотношение волновых сопротивлений щелей удовлетворяет записанному условию, а их электрические длины одинаковы. Используя соотношения (1) и (3) для коэффициентов отражения, можно показать, что при этих условиях ,т.е система как бы внутренне согласована.

В итоге получаем уравнение  дисперсии основной волны в ЗС с неравными щелями связи.

                    (8)

 Преобразуем теперь  выражение для замедления в ЗС с неравными щелями.

Учитывая, что

,

 

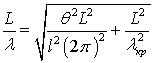где , , ― критическая длина волны, получаем окончательное выражение для замедления:

,                 (9)

  где

.

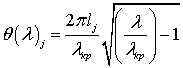Рассмотрим теперь обычно  применяемую систему с одинаковыми щелями связи (отрезки 2 и 4), для которой , . Уравнение  дисперсии для неё имеет известный вид 

                                 (10)

для сдвига фазы  на один шаг, т.е. половину периода. Его можно также преобразовать к виду, аналогичному (8) для сдвига фазы на полный период:

                        (11)

Результаты расчета дисперсионных характеристик для ЗС с равными и неравными щелями связи приведены на рис 5,6.

 

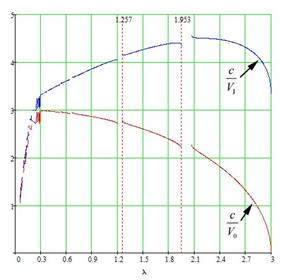
Рис. 5. Замедление для системы с равными щелями связи для 0-ой и 1-ой пространственных гармоник

 

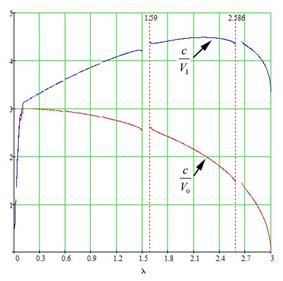
Рис. 6. Замедление для системы с неравными щелями связи для 0-ой и 1-ой пространственных гармоник

 

Видно, что вторая полоса пропускания для ЗС с неравными щелями больше, чем первая и замедление в этой полосе на 1-ой пространственной гармонике может слабо меняется с частотой, если подобрать соответствующие геометрические размеры ЗС. Поэтому можно ожидать большую полосу усиления в ЛБВ  при работе  во второй полосе пропускания

 Сравнивая приведенные на рис. 5,6 результаты, можно сказать, что при размерах одного порядка система с неравными щелями связи позволяет работать на более высоких частотах в широкой полосе пропускания. Это может оказаться полезным для ЛБВ миллиметрового диапазона.

Заключение

 С использованием волноводно-резонаторной мо­дели ЗС исследованы частотные свойства ЗС петляющего типа с неравными щелями связи. Показано, что в таких системах существует возможность увеличить полосу усиления в ЛБВ  во второй полосе пропускания ЗС. Из полученных результатов видно, что при  одинаковых размерах ЗС  с неравными щелями позволяет работать на более высоких частотах и в более широкой полосе пропускания, чем обычная система с одинаковыми щелями связи.

Работа выполнена при  поддержке Российского фонда фундаментальных исследований (проект №10-02-00859).

 

Литература

1. Мухин С В., Ломакин О.Е., Солнцев В.А. // РЭ. 1988. Т. 33. № 8. С. 1637.

2. Силин Р.А., Чепурных И.П. // РЭ. 1990. Т. 35. № 5. С. 939.

3. Солнцев В.А., Никонов Д.Ю. // РЭ. 2006. Т. 51. №8. С.1008–1018

4. Лебедев И.В. Техника и приборы СВЧ. М.: Выс­шая школа, 1970. Т. 1.