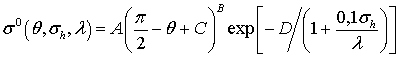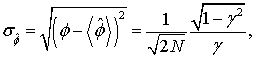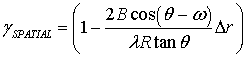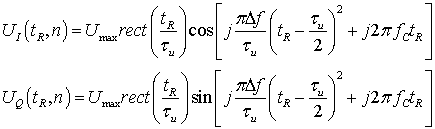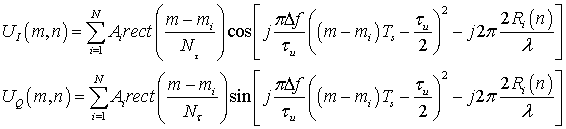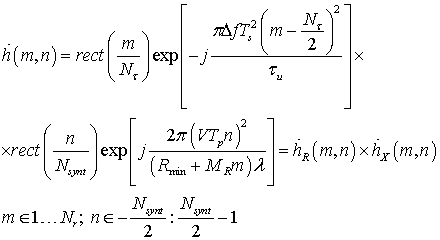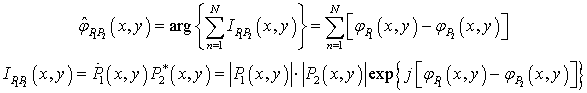Моделирование алгоритмов обработки сигналов двухпроходного авиационного интерферометрического РСА

УДК 621.396.96

МОДЕЛИРОВАНИЕ АЛГОРИТМОВ ОБРАБОТКИ СИГНАЛОВ ДВУХПРОХОДНОГО АВИАЦИОННОГО ИНТЕРФЕРОМЕТРИЧЕСКОГО РСА

П. Е. Шимкин, А. И. Баскаков

Национальный исследовательский университет «МЭИ»

Статья поступила в редакцию 8 октября 2014 г., после доработки - 30 сентября 2015 г.

Аннотация. В работе проведено имитационное моделирование алгоритмов интерферометрической обработки сигналов в пакете прикладных программ MATLAB и обоснован выбор основных параметров одного из возможных вариантов построения интерферометрического РСА.

Ключевые слова: интерферометрический РСА с «мягкой базой», разность фаз, трехмерное изображение, рельеф поверхности.

Abstract: The simulation algorithms interferometric signal processing in the application package MATLAB was made in the paper and choice of the basic parameters of one of the possible variants of interferometric SAR was justified.

Key words: interferometric SAR with a "soft base", the phase difference, three-dimensional images, surface relief.

Введение

В последнее время, развитие теоретических принципов и технических возможностей построения радиолокаторов с синтезируемой апертурой антенны (РСА) позволило получать радиолокационные изображения (РЛИ) с разрешающей способностью порядка единиц метров и выше. Но дальнейшее повышение геоинформативности авиационных и космических средств дистанционного зондирования Земли (ДЗЗ) связано с развитием теории и техники получения детального рельефа местности и формированием трехмерного изображения [1]. Поэтому, на сегодняшний день, основной задачей является создание перспективных комплексов, способных с высокой точностью и высокой разрешающей способностью формировать кроме привычных двумерных РЛИ также и трехмерные изображения земной поверхности. Одним из решений построения такого комплекса является двухпроходный интерферометрический РСА (ИРСА). Он может быть выполнен как в авиационном, так и в космическом варианте построения.

Такой комплекс является сложной системой, поэтому реальная проверка алгоритмов его работы затруднена из-за финансовых или технических возможностей. Также, реальные эксперименты могут выполняться только в небольшом диапазоне вариаций условий наблюдения, что недостаточно для полного анализа системы. В связи с этим, создание имитационной модели и проведение компьютерного моделирования являются одним из основных и эффективных методов изучения такой сложной системы.

Геометрия визирования

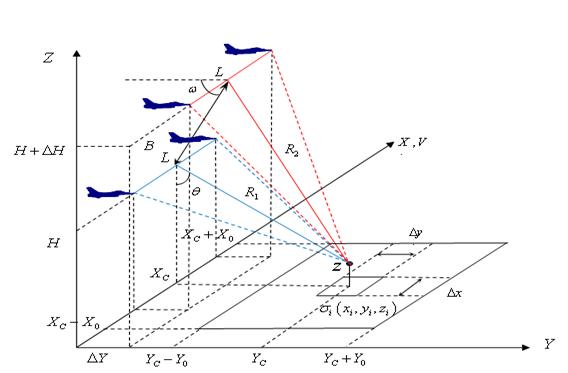
Моделируется двухпроходный авиационный ИРСА, геометрия визирования которого изображена на рис. 1, где синим цветом условно указан первый проход носителя, красным – второй. Наблюдение за исследуемой поверхностью происходит в режиме бокового обзора с помощью одного носителя РСА, но за два прохода, так называемый режим «мягкой базы». В двух проходах носитель РСА движется вдоль координаты с постоянной скоростью , формируя синтезированную апертуру , но с различными положениями по высоте и направлению поперечному движению. На рис. 1 это проявляется в наличии сдвигов во втором проходе и . В результате образуется интерферометрическая пара антенн, разделенных базой интерферометра . Следует отметить, что в общем случае наличие сдвигов и приводит к наклону базы к горизонтали, обозначим этот угол . В большинстве случаев принимает значения (строго горизонтальное смещение) и (строго вертикальное смещение). В статье рассматривается случай строго вертикального смещения. На рис. 1 – размеры элемента разрешения по дальности и по азимуту, и – координаты центра кадра; и – размеры кадра по соответствующим координатам.

Рис. 1. Геометрия визирования двухпроходного ИРСА.

Структура модели

Процесс имитационного моделирования может быть представлен в виде блок-схемы (рис. 2), где ЦМР – цифровая модель рельефа, РЛИ – радиолокационное изображение, ИРФ – интерферометрическая разность фаз.

Рис. 2. Структурная схема имитационного моделирования ИРСА

Цифровая модель рельефа

Происходит формирование радиолокационного рельефа исследуемой поверхности согласно феноменологической модели [1]. Каждый элемент разрешения на поверхности Земли представляется набором отдельных парциальных отражателей, распределенных по нормальному закону, на которые накладываются известные из экспериментальных результатов условия рассеяния.

В качестве исходных данных для имитационной модели двухпроходного интерферометра возьмем модель рельефа, изображенную на рис. 3. Согласно рис. 3 центр кадра имеет координаты м, м. Размеры кадра определяются пятном облучения диаграммы направленности антенны на поверхности.

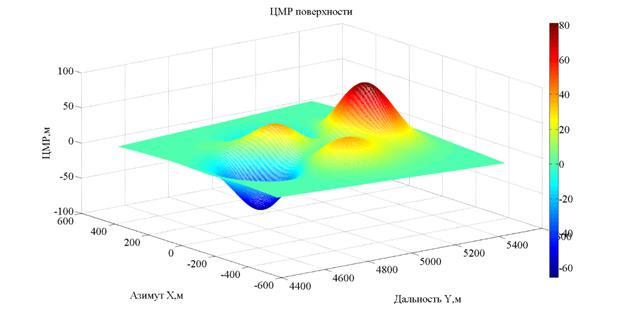
Рис. 3. Цифровая модель рельефа поверхности

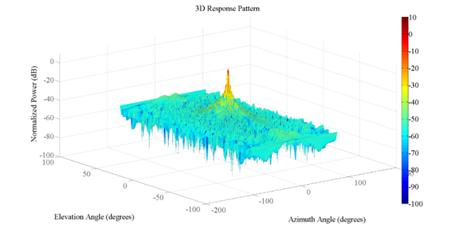
В качестве модели антенны используем фазированную антенную решетку (ФАР), вид и ДНА которой приведены на рис. 4.

Рис. 4. Внешний вид и ДНА

Ширина луча в обоих плоскостях составляет примерно . При дальностях порядка 7,5 км и высоте полета 5 км получим кадр размером м. Поэтому, элементарные отражатели, формирующие распределенную цель, будут расположены на поверхности в интервале горизонтальных дальностей м и азимута м. Тип поверхности представляет собой сухую почву, по виду – овражно-холмистая с среднеквадратической ординатой мелкой шероховатости см и перепадами неровностей рельефа от до 80 м.

Основной параметр, характеризующий распределенную цель – удельная эффективная поверхность рассеяния (УЭПР). В настоящее время для приближенности к реальному миру разработчики используют экспериментально полученные натурные модели УЭПР, хорошо зарекомендовавшие себя на протяжении многих лет. Одной из таких моделей является, разработанная научно-исследовательским институтом Georgia Tech (Georgia Tech Research Institute, Atlanta, Georgia, USA) модель УЭПР для различного типа поверхностей [2]. Данная модель учитывает среднеквадратическую ординату мелкой шероховатости поверхности , угол падения на поверхность , отсчитываемый от вертикали и длину волны , и имеет следующий вид [3] (1):

(1)

где – коэффициенты эмпирической модели. В [3, 4] приведены значения для этих констант в частотном диапазоне частот от 3 до 95 ГГц для некоторых типов поверхностей.

На рис. 5 представлена зависимость УЭПР от угла падения для сухой почвы на частоте 10 ГГц.

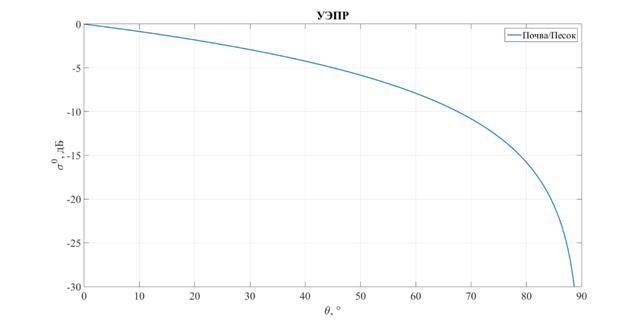
Рис. 5. Зависимость УЭПР от угла падения для сухой почвы

Параметры двухпроходного ИРСА

Рабочая частота передатчика РСА ГГц (соответствующая длина волны см). Например, для получения разрешения по координате наклонной дальности м и, следственно, горизонтальной дальности 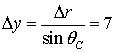м используется зондирующий ЛЧМ сигнал с шириной спектра МГц.

Разрешение вдоль координаты , линии пути (азимуту) достигается за счет применения техники синтезированной апертуры. Например, для достижения разрешающей способности по азимуту примерно равной разрешающей способности по горизонтальной дальности необходимо синтезировать апертуру длиной м.

Длительность импульса можно выбрать из скважности . Пусть
, тогда с учетом того что мкс, мкс.

Период повторения зондирующих импульсов самолетного РСА выбирается из условия однозначности формирования РЛИ как по азимуту, так и по дальности (2):

(2)

где , скорость полета носителя порядка 250 м/с, типичный размер антенны авиационной РЛС м, мкс – время работы антенного переключателя. Тогда: мкс. Пусть мкс.

Выбор оптимальной базы интерферометра

Из рис. 1 может быть получено соотношение между параметрами отклонения базы , угла визирования и разности фаз :

(3)

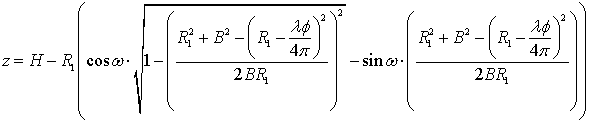
Из (3) видно, что что ордината элемента разрешения z является функцией параметров: высоты носителя , наклонной дальности азимутального угла , размера базы и разности фаз . Поэтому общую погрешность измерения высоты элемента разрешения, с предположением о некоррелированности отдельных составляющих, можно записать в виде [5]:

(4)

где – дисперсия оценки ординаты элемента разрешения из-за погрешности оценки разности фаз; – дисперсия оценки ординаты элемента разрешения из-за погрешности задания угла наклона базы; – дисперсия оценки ординаты элемента разрешения из-за погрешности измерения высоты орбиты; – дисперсия оценки ординаты элемента разрешения из-за погрешности измерения расстояния до элемента разрешения; – дисперсия оценки ординаты элемента разрешения из-за погрешности неточного знания размера базы.

Выбор наиболее выгодного режима интерферометрического зондирования сводится к определению параметров съемки, минимизирующих вышеперечисленные погрешности. Например, погрешность, связанная с погрешностью оценки разности фаз, определяется следующим выражением (5):

(5)

Так как потенциальные точностные характеристики определяются только через , то наибольший интерес представляет анализ погрешности, связанной именно с оценкой ИРФ .

Согласно [6], оценку ИРФ можно провести использую метод «оценки максимального правдоподобия (ОМП)». Тогда, среднеквадратическое отклонение ИРФ можно оценить следующим выражением (6):

(6)

где – кратность некогерентного накопления, – коэффициент корреляции.

Интерферометрическая когерентность или коэффициент корреляции между двумя снимками, составляющими интерферометрическую пару, в общем случае состоит из четырех составляющих [7]: декорреляция за счет пространственного разнесения двух антенн – ; декорреляция, вследствие наличия мелкой шероховатости поверхности – ; временная декорреляция, связанная с физическими изменениями на поверхности между двумя наблюдениями – ; декорреляция за счет теплового шума в системе РСА – . Для простоты .

Результирующий коэффициент корреляции представляется в виде произведения вышеперечисленных составляющих:

(7)

Получены аналитические выражения каждого из факторов. При расчетах было принято предположение о представлении реальной поверхности в виде распределённой радиолокационной цели, для которой используется феноменологическая модель из набора независимых парциальных отражателей внутри элемента разрешения. Также было использовано описание плотности распределения ординат парциальных отражателей внутри элемента разрешения в виде нормального закона. Результаты расчетов каждой из составляющих (7):

;	(8)
;	(9)
;	(10)
;	(11)

где – разрешающая способность по наклонной дальности; – среднеквадратическая ордината мелкой шероховатости поверхности; – разрешающая способность по азимуту; – отношение сигнал/шум.

Получив результирующий коэффициент корреляции в виде произведения указанных составляющих и, подставив их в (6) можем получить выражение для СКО оценки ИРФ. Затем подставляя (6) в (5) получим зависимость СКО оценки ординат рельефа через СКО оценки ИРФ. В связи с громоздкостью этих выражений, их полное отображение в документе не представляется возможным.

Для выбранных параметров комплекса ИРСА и моделируемой поверхности, имеем следующую зависимость потенциальной точности оценивания рельефа поверхности от базы интерферометра (рис. 6).

Рис. 6. СКО оценивания рельефа в зависимости от размера базы при параметрах: МГц; ; ; км; дБ;

; см.

Из рис. 6 видно, что оптимальным является смещение носителя во втором проходе на 7,5 м, при котором потенциальное СКО оценки рельефа примерно 2 м.

Моделирование траекторного сигнала

Для начала необходимо определить некоторые параметры, характеризующие сигналы на входе процессора регистрации и обработки траекторного сигнала РСА [8].

Имеем:

см и ГГц – длина волны РСА и несущая частота зондирующего сигнала;

мкс – длительность зондирующего импульса;

МГц – ширина спектра зондирующего ЛЧМ сигнала;

мкс и кГц – частота и период повторения импульсов;

МГц; нс – частота и период дискретизации принятых сигналов;

– число отсчетов на длительности импульса;

м/с – скорость полета носителя;

с – время синтеза;

– число синтезируемых импульсов;

м – шаг дискретизации по наклонной дальности (масштаб голограммы и РЛИ);

м и м – наклонные дальности первого и последнего отсчета сигналов в строке радиолокационных данных;

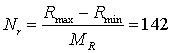– число отсчетов в стробе приема по дальности.

Излучаемые, а также принимаемые двумерные сигналы рассматривают раздельно в координатах «быстрого времени» (по наклонной дальности) и «медленного времени» по азимуту , которое можно выразить через номер зондирующего импульса . Излучаемый сигнал представляет собой последовательность зондирующих импульсов, каждый из которых характеризуется в «быстром времени» выражением (12):

(12)

где при .

Принимаемый комплексный видеосигнал на выходе фазового детектора приемника является суперпозицией сигналов, отраженных от элементарных отражателей, расположенных в пределах кадра формируемой поверхности (13):

(13)

где 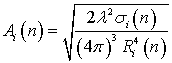– амплитудный множитель, нормированный на излученную передатчиком мощность и коэффициент усиления антенны; –УЭПР отражателя; ; – текущая наклонная дальность до цели; – номер отсчета дальности для переднего фронта принятого сигнала от цели. В общем случае зависит от положения РСА по азимуту (номера строки дальности ), что вызывает эффект «миграции» дальности.

Обработка траекторного сигнала и формирование РЛИ

Обработка траекторного сигнала РСА происходит по алгоритму прямой свертки принимаемого сигнала с комплексно сопряженной двумерной дискретной опорной функцией.

Для определения вида опорной функции, аппроксимируют временной закон текущей наклонной дальности квадратичным членом [9]. Азимутальные отсчеты дальности и фазы определяются формулами:

(14)

Тогда, двумерная опорная функция будет иметь вид (15) [8]:

(15)

Прямая свертка двумерных дискретных сигналов выполняется в два этапа – сначала производится свертка по дальности, а затем по азимуту. Наиболее распространенным и одним из самых производительных алгоритмов вычисления свертки является алгоритм быстрой свертки. Преимущества быстрой свертки реализуются при использовании для дискретного преобразования Фурье алгоритма быстрого преобразования Фурье (БПФ, Fast Fourier Transform – FFT). Таким образом, свертки по дальности и азимуту (16):

(16)

где – прямое быстрое преобразование Фурье; – обратное быстрое преобразование Фурье.

Также, при наличии эффекта миграции дальности, необходимо между операциями «свертки по азимуту» и «свертки по дальности» провести операцию компенсации миграции дальности. Алгоритмы компенсации миграции дальности (Range Cell Migration – RCM) подробно описаны в [3] и [10].

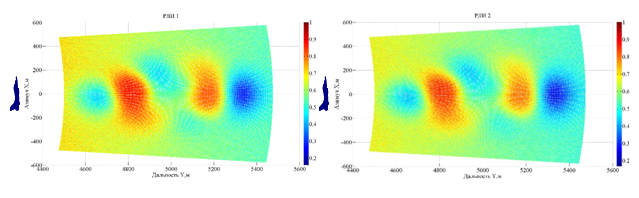
Результатом моделирования алгоритмов является пара РЛИ исследуемой поверхности (рис. 7). При выбранных геометрии облучения и неровности поверхности эффект затенения отсутствует.

Рис. 7. РЛИ поверхности, полученное при первом (а) и втором (б) проходах носителя

Вычисление интерферометрической разности фаз

Обозначим радиолокационные изображения, полученные при первом и втором проходах носителя и . Тогда ИРФ определяется следующим образом (17):

(17)

где – кратность некогерентного накопления.

На рис. 8 показана ИРФ для моделируемой поверхности.

Рис. 8. ИРФ моделируемой поверхности

Рис. 9 иллюстрирует эффект влияния отношения сигнал/шум (фон/шум) на вид интерферограммы. Видно, что при значительном ухудшении отношения фон/шум наблюдается полное разрушение ИРФ.

Рис. 9. Влияние отношения фон/шум для ИРФ, полученной с помощью двухпроходного интерферометра

Устранение составляющей плоской поверхности Земли

Вычисленная ИРФ включает в себя и составляющую плоской поверхности Земли. Обозначим ее . Операция устранения заключается в вычитании значений из :

(18)

Рассчитаем ИРФ для плоской поверхности Земли . Разница в наклонных дальностях до каждого элементарного отражателя (рис. 1) аппроксимируется формулой . Тогда, формула разности фаз на двух проходах носителя (19):

(19)

Для плоской поверхности Земли угол меняется только вследствие изменения координаты горизонтальной дальности . Поэтому:

(20)

Полученные значения также необходимо свернуть в интервал . На рис. 10 изображена рассчитанная по (20) ИРФ плоской поверхности Земли.

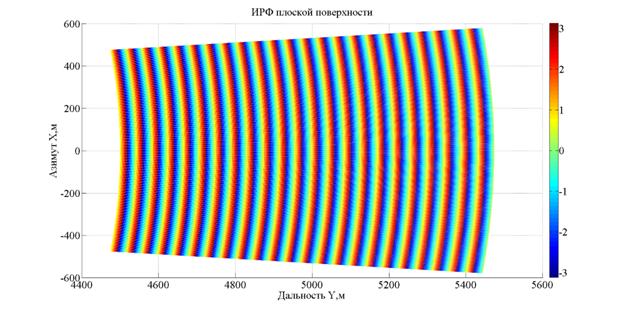
Рис. 10. ИРФ плоской поверхности Земли

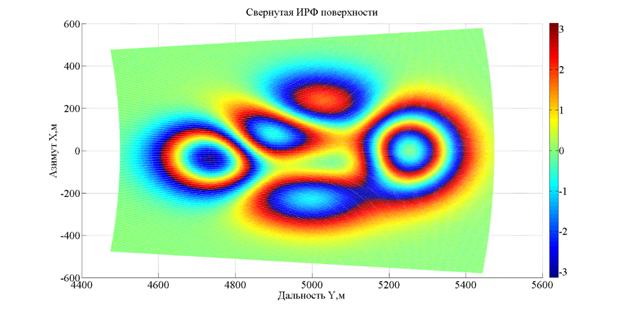
Рис. 11. ИРФ без составляющей плоской поверхности, «свернутая» ИРФ

Результат устранения плоской поверхности Земли из на рис. 11, видно, что необходима операция раскрытия фазовой неоднозначности.

Раскрытие фазовой неоднозначности

Возникновение фазовой неоднозначности связано с тем, что фазовые значения комплексного радиолокационного сигнала вычисляются в диапазоне , а высотная разностнофазовая составляющая интерферограммы при больших перепадах рельефа может изменяться на несколько интервалов . Поэтому для получения данных об относительных высотах рельефа после вычисления значения фаз необходимо устранить фазовую неоднозначность, кратную интервалу .

Задача развертывания фазы заключается в восстановлении истинной разности фаз по значениям, приведённым к промежутку .

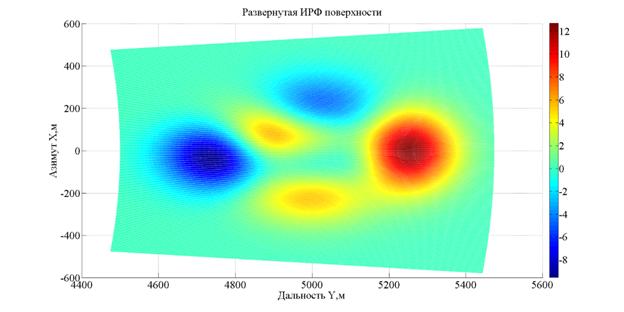
Рис. 12. Развернутая ИРФ

Решить такую задачу можно, например, с помощью одного из известных алгоритмов 2D–разворачивания фазы – алгоритм Гольдштейна-Вернера-Зебкера, который является типичным представителем методов следящих за путями. Вкратце, алгоритм основывается на том, что свернутую фазу можно развернуть путем интегрирования разницы свернутых фаз между соседними элементами. Он хорошо работает при предположениях о том, что разница фаз между соседними пикселями меньше и отсутствия резких скачков (перепадов) рельефа, что вызовет множество оборотов фазы. Подробное описание алгоритма можно найти в [11].

Результат разворачивания фазы представлен на рис. 12.

Масштабирование для получения карты высот

Существует однозначная связь между изменениями ИРФ и изменениями высоты рельефа поверхности. Из геометрии визирования (рис. 1), опуская промежуточные преобразования можно получить зависимость между изменениями ИРФ каждого пикселя и изменениями высоты рельефа (21):

(21)

где – коэффициент масштабирования ИРФ.

Выражение (14) является основным результатом ИРСА. Оно позволяет оценить высоту рельефа по измеренной ИРФ, предварительно прошедшей процедуру устранения составляющей плоской поверхности Земли и умноженной на масштабирующий коэффициент.

В результате вычислений по формуле (21) была получена абсолютная карта высот, совпадающая с исходными данными рельефа моделируемой поверхности. При этом СКО определения высоты составила м, что соизмеримо с потенциальной точностью двухпроходного авиационного ИРСА.

Выводы

Разработана имитационная модель, позволяющая гибко изменять геометрию наблюдения и параметры ИРСА. Результаты обработки сигналов выбранного интерферометрического комплекса РСА показали возможность использования модели в качестве инструмента для анализа поведения системы при различных моделируемых ситуациях.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проекты № 13-0800375а, 13-08-97538), Российского научного фонда (проект № 14-49-00079) и Государственного задания в сфере научной деятельности в проектной части № 8.152.2014/К.

Литература

1. Баскаков А.И., Жутяева Т.С., Лукашенко Ю.И. Локационные методы исследования объектов и сред. Учебник для вузов. – М: Изд-во «Академия», 2011.

2. Currie N.C, Zehner S.P. MMW Land Clutter Model. IEE Radar 82 International Symposium, London, September 1982

3. Richards, M.A., Scheer, J.A., and Holm, W.A. Principles of modern radar: basic principles. SciTech Publishing, Raleigh, NC, 2010, p. 202-208

4. Currie N.C. MMW Clutter Characteristics, Chapter 5 in Principles and Applications of Millimeter-Wave Radar, Ed. N.C. Currie and C.E. Brown, Artech House, Norwood, MA, 1987

5. Баскаков А.И., Шимкин П.Е. Исследование потенциальной точности определения местного рельефа авиационным интерферометрическим РСА при переднебоковом обзоре // Радиотехника. 2013. №10. С. 71 – 74 .

6. Rodrigeuz E., Martin J.M. Theory and design of interferometric synthetic aperture radars. // IEE Proceeding Part. F. 1992, № 2, v.139 p.147-159.

7. Zebker H.A., Villasenor J. Decorralation in interferometric radar echoes. // IEEE Transactions on geoscience and remote sensing, 1992, № 5, vol.30 p 950-959.

8. Верба В.С., Неронский Л.Б., Осипов И.Г., Турук В.Э. Радиолокационные системы землеобзора космического базирования. Под общей редакцией Вербы В.С. – М.: Радиотехника, 2010.

9. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Учебное пособие для вузов. / Под ред. Г. С. Кондратенкова. – М.: «Радиотехника», 2005.

10. Школьный Л.А., Толстов Е.Ф., Детков А.Н., Карпов О.А., Яковлев А.М., Титов М.П., Филатов А.А., Тонких А.Н., Цветков О.Е., Архангельский А.С. Радиолокационные системы воздушной разведки, дешифрование радиолокационных изображений. /Под ред. Школьного Л.А. – М.: Изд-во ВВИА им. проф. Н.Е. Жуковского, 2008.

11. Goldshtein R.M., Zebker H.A., Werner C.L. Satellite radar interferometry: two-dimensional phase unwrapping. Radio Science, Vol. 23, № 4, 1988, p. 713–720.