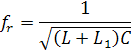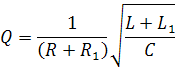ЭКВИВАЛЕНТНАЯ СХЕМА ПЛАНАРНОГО ОТКРЫТОГО РЕЗОНАТОРА, ВЗАИМОДЕЙСТВУЮЩЕГО С ДЖОЗЕФСОНОВСКИМ ПЕРЕХОДОМ В ТЕРАГЕРЦОВОМ ДИАПАЗОНЕ ЧАСТОТ

 

А. В. Снежко^1,2, В. В. Павловский¹, В. Н. Губанков¹

¹Институт радиотехники и электроники им. В.А. Котельникова РАН

²Московский физико-технический институт (ГУ)

 

Статья поступила в редакцию 13 ноября 2015 г.

 

Аннотация. В работе представлена эквивалентная схема открытого резонатора, взаимодействующего с бикристаллическим джозефсоновским переходом из YBa₂Cu₃O_7-x. Разработанная на основе эквивалентной схемы модель используется в методике частотной характеризации резонаторов с помощью нестационарного эффекта Джозефсона. Продемонстрирована применимость модели в области частот от 50 ГГц до 700 ГГц.

Ключевые слова: терагерцовая электроника, сверхпроводимость, джозефсоновский переход.

Abstract. Equivalent circuit based model of planar open ring resonator interacting with bicrystal YBa₂Cu₃O_7-x Josephson junction was developed. This model is used for frequency characterization of planar open ring resonators by the ac Josephson effect. Validity of the model in frequency range from 40 GHz to 700 GHz was demonstrated.

Key words: terahertz electronics, superconductivity, Josephson junction.

 

Введение

Развитие технологии субмикронных размеров позволило создавать материалы, обладающие необычными электромагнитными свойствами. Ярким примером таких материалов являются метаповерхности, благодаря которым существует возможность наблюдать отрицательное преломление электромагнитной волны, и которые можно использовать для создания идеальной линзы, оптической маскировки и т.д. [1]-[2] В отличие от традиционных оптических устройств, где модифицирование волнового фронта (изменение фазы, амплитуды, поляризации) происходит благодаря распространению электромагнитной волны в диэлектрической среде, в метаповерхностях оптические свойства изменяются скачкообразно, на масштабе длины падающей волны. Обычно метаповерхности представляют собой массив планарных металлических антенн, при рассеивании на которых формируется и модифицируется волновой фронт падающей волны. Варьирование размеров, формы антенны в массиве позволяет формировать волновой фронт желаемым способом [3]. Поэтому важной задачей при создании метаповерхности с искомыми свойствами является частотная характеризация составляющих её одиночных антенн. В оптической области частот существуют эффективные спектральные методы, позволяющие исследовать интегральные характеристики двумерных массивов микроантенн. При частотах ниже 100 ГГц для частотного анализа успешно применяются векторные анализаторы цепей [5], в которых используются радиофизические методы исследования. В то же время в более высокочастотном диапазоне возможно совместное исследование как интегральных характеристик метаповерхности квазиоптическими методами, так и локальных параметров составляющих метаповерхность элементов радиофизическими методами. Таким образом, актуальной задачей является создание спектральных методик, покрывающих область частот от 100 ГГц до нескольких единиц терагерц. Одним из новых способов проведения частотного анализа в этом труднодоступном терагерцовом диапазоне является метод на основе джозефсоновской спектроскопии, в котором чувствительным элементом является джозефсоновский переход. Возможности джозефсоновской спектроскопии уже были успешно продемонстрированы как для исследования источников электромагнитного излучения в терагерцовой области частот [6], так и для частотной характеризации различных планарных электродинамических систем в диапазоне частот от 50 ГГц до 1.2 ТГц [7]-[9]. В частности, данная методика позволяет разрабатывать эквивалентные схемы пассивных элементов, которые могут быть использованы при конструировании метаповерхностей с заданными свойствами. В предлагаемой работе представлена эквивалентная схема планарного открытого резонатора в области частот от 50 ГГц до 700 ГГц, разработанная с помощью методики на основе нестационарного эффекта Джозефсона.

2. Детали эксперимента и эквивалентная схема

В работе использовались бикристалические ДП из высокотемпературного сверхпроводника (ВТСП) YBa₂Cu₃O_7-x с критической температурой T~90 K, напыленные на диэлектрические подложки из MgO или NdGaO₃ (рис.1).

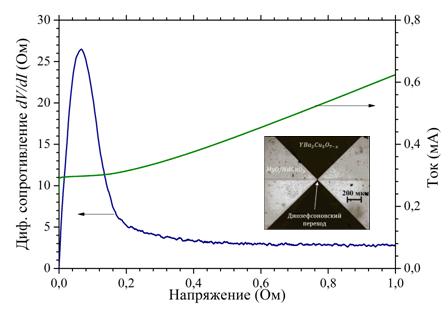
Рис.1. Вольтамперная характеристика I(V) и зависимость дифференциального сопротивления R_d(V)=dV/dI
автономного бикристаллического джозефсоновского перехода из YBa₂Cu₃O_7-x
ри температуре T=5 K в магнитном поле H=80 Гс.
На вставке приведена фотография джозефсоновского перехода.

Как было показано, такие ДП описываются резистивной моделью, а джозефсоновские колебания существуют вплоть до 5 ТГц [10], что позволяет использовать данные ДП для частотной характеризации резонаторных структур в области частот до нескольких единиц терагерц. Характеристические напряжения V_с=I_сR_n ДП варьировались от 0.3 до 3 мВ при температуре T=5 K, сопротивления в нормальном состоянии – от 0.3 до 50 Ом. Резонаторные системы представляли собой медные планарные квадратные резонаторы с разрезом (рис.2а), напыленные на сапфировые подложки. Размеры стороны квадрата резонатора варьировалась от 30 мкм до 500 мкм. Резонатор помещался вблизи слабой связи ДП (рис.2б). Подводящие электроды ДП были выполнены в виде треугольников с углами при вершинах 90° и длинами высот 1000 мкм.

 

а	б

Рис.2. Фотография планарного квадратного резонатора с длиной стороны 33 мкм;
фотография джозефсоновского перехода и приложенного к нему резонато­ра с длиной стороны 366 мкм (б).

 Такая форма обеспечивала плавно меняющийся с частотой импеданс электродов, на фоне которого чётко проявляются особенности, связанные с резонансами исследуемых структур. ДП с исследуемой структурой монтировался в криогенной вставке в сосуд Дьюара с жидким гелием, Температура ДП варьировалась от 5 К до 90 К. Частотная полоса измерения изменялась с использованием магнитного поля [7].

Для проведения измерений статических характеристик использовался режим задания тока смещения через ДП. С помощью малошумящей электроники и синхронного детектора проводились измерения зависимости дифференциального сопротивления ДП R_d(I)=dV/dI от тока I при частоте 350 кГц, для уменьшения влияния низкочастотных флуктуаций тока в ДП на измеряемые характеристики. На основе этих данных, а также данных измерения вольтамперной характеристики ДП V(I) строилась зависимость R_d(V) ДП. Для интерпретации полученных результатов использовалась эквивалентная схема ДП, взаимодействующего с резонатором, представленная на рис. 3.

 

Рис. 3. Эквивалентная схема джозефсоновского перехода, взаимодействующего с планарным открытым резонатором квадратной формы.

Эквивалентная схема основана на резистивной модели ДП, в которой переход представлен в виде джозефсоновской слабой связи, ток через которую I связан с разностью фаз сверхпроводящих электродов j соотношением I=I_s×sinj, и соединённым параллельно с ней резистором R_n, сопротивление которого равно сопротивлению ДП в нормальном состоянии. Влияние широкополосного поглощения в материале ДП учитывается цепочкой R_cC_c. При необходимости для более точного описания зависимости R_d(V) автономного ДП вводится необходимое количество последовательных цепочек RLC, включённых параллельно (на рис. 3 не показаны). Рамкой на рис. 3 выделена часть эквивалентной схемы, влияющая на характеристики ДП при присоединении к нему резонатора. Резонатор представлен колебательным контуром LL₁RR₁C, в котором LR и L₁R₁ представляют индуктивности и электромагнитные потери в отдельных частях резонатора, разделённых областями перекрытия резонатора с электродами ДП, а С определяется, в основном, разрезом резонатора. Потери в резонаторе связаны как с омическим сопротивлением материала, так и с электромагнитным излучением. Возбуждение колебаний в резонаторе джозефсоновским осциллятором осуществляется через ёмкостную связь C₀. Учет тепловых флуктуаций нормальных квазичастиц осуществляется путем присоединения к каждому сопротивлению R источника флуктуационных токов I_f. Для вычисления ВАХ и R_d(V) решалась система стохастических дифференциальных уравнений, соответствующих данной эквивалентной схеме [11].

3. Результаты измерений и их обсуждение

При взаимодействии ДП с планарным квадратным резонатором с разрезом, в последнем джозефсоновскими осцилляциями возбуждается фундаментальная мода [8] с частотой f_r. При этом на периметре резонатора укладывается половина длины волны излучения. На зависимости дифференциального сопротивления от напряжения ДП R_d(V) наблюдаются ярко выраженные особенности вблизи напряжения, которое связано с резонансной частотой соотношением Джозефсона V=hf_r/2e, где h - постоянная Планка, e – заряд электрона. На рис. 4,5 пунктирными линиями представлены результаты измерения зависимостей R_d(V) ДП, взаимодействующего с планарными квадратными резонаторами с разрезом с размерами сторон квадратов 366 мкм и 33 мкм, а сплошными линиями – результаты вычислений с использованием эквивалентной схемы.

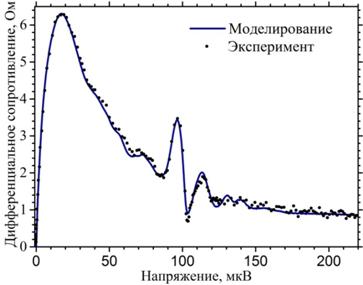
Рис. 4. Зависимость R_d(V) джозефсоновского перехода, взаимодействующего с пла­нарным квадратным резонатором с разрезом с размером стороны квадрата d=366 мкм при температуре T=5 K. Пунктирная линия – результаты измерения, сплошная линия – результаты расчётов.

 

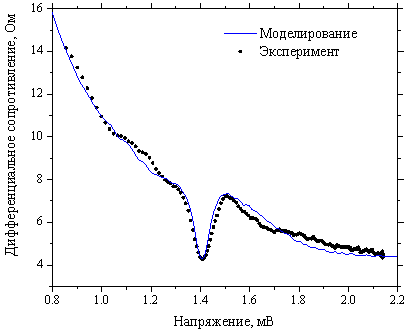
Рис. 5. Зависимость R_d(V) джозефсоновского перехода, взаимодействующего с пла­нарным квадратным резонатором с разрезом с размером стороны квадрата d=33 мкм при температуре T=5 K. Пунктирная линия – результаты измерения, сплошная линия – результаты расчётов. 

Следует отметить различие в форме особенностей на рис. 4 и 5, которое связано с разными механизмами взаимодействия резонаторов с ДП при низких и высоких частотах. Длина волны, соответствующая резонансу, наблюдаемому на рис. 4, равна 3928 мкм, что превышает суммарный размер подводящих электродов (2000 мкм), В этом случае справедливо квазистатическое описание системы, состоящей из резонатора и ДП с подводящими электродами, и все элементы схемы, изображённой на рис. 4, имеют соответствующие геометрические эквиваленты. В частности, C₀ определяется площадью перекрытия резонатора с электродами, а L, L₁, R, R₁ – индуктивности и сопротивления соответствующих частей резонатора, причём можно считать L₁/L=R₁/R=1/3. При условии C₀/C «1 (т.е. в случае слабой связи резонатора с ДП) адмиттанс части эквивалентной схемы Y(f) между точками 1 и 2 на рис. 3 можно представить в следующем виде:

,

(1)

где  – плавно меняющийся с частотой адмиттанс, влияние которого на зависимость дифференциального сопротивления от напряжения ДП не приводит к появлению явных особенностей. Второй член в выражении описывает адмиттанс последовательного RLC контура, с резонансной частотой:

(2)

и добротностью:

(3)

Применимость приближения (1) определяется малостью параметра

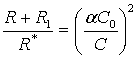         ,                                                                                                                          (4)

 

где a=L/(L+L₁)= R/(R+R₁)=0.25.

В результате подгонки вычисленной зависимости к измеренной для резонатора с длиной стороны квадрата d=366 мкм были получены параметры эквивалентной схемы f_r=47,8 ГГц и Q=14. Этот резонатор имеет ширину микрополоска 60 мкм и таким образом его перекрытие с электродами ДП осуществляется по двум прямоугольным треугольникам с катетами длиной 60 мкм. Соответственно общая площадь перекрытия составляет 3.6·10^-9 м². Величина диэлектрической проницаемости материала PMMA, заполняющего пространство между резонатором и электродами, составляет 2.6. Толщина диэлектрического слоя составляет более 10 мкм [12]. Таким образом C₀ не превышает 8·10^-15 фФ. Величина С, полученная из f_r и Q составляет 21 фФ. Следовательно, параметр малости (4) не превышает 10^-2, и приближение (1) в случае резонатора с длиной стороны 366 мкм должно выполняться с достаточно высокой точностью. В этом случае резонатор ведёт себя как последовательный RLC контур, включённый параллельно ДП. Отметим, что рассматриваемый случай сводится к рассмотренному ранее (см [7] и ссылки) и форма особенности на зависимости R_d(V), связанная с возбуждением резонатора, в окрестности напряжения V_r=hf_r/2e имеет выраженную антисимметричную форму, аналогичную формам особенностей, связанных с резонансами в логопериодической антенне, интегрированной с ДП.

В случае, когда длина волны много меньше размеров электродов, ёмкость связи уже нельзя рассматривать как сосредоточенную только в области перекрытия резонатора с электродами, и может реализоваться случай C₀/C ³1, что приведёт к существенному изменению формы резонансной особенности зависимости R_d(V). Такой случай реализуется для резонатора с длиной стороны 33 мкм (рис. 5). В этом случае достаточно хорошее совпадение расчётной и экспериментальных характеристик достигается при значениях C₀=5 фФ и С=1.3 фФ. При этом L₁/L=0.06, т. е. индуктивность резонатора также нельзя представлять в виде сосредоточенных параметров, относящихся к различным его частям. В результате для резонатора с длиной стороны 33 мкм были получены следующие параметры эквивалентной схемы f_r=698,9 ГГц, Q=43.

4. Заключение

В работе была представлена модель планарного открытого резонатора, взаимодействующего с бикристаллическим ДП. Показано, что при расчётах с использованием этой модели имеет место особенность при напряжении на ДП, связанном с резонансной частотой резонатора соотношением Джозефсона. При этом разработанная модель даёт количественное описание наблюдаемого на эксперименте существенного изменения формы особенности при переходе от квазистатического режима взаимодействия резонатора с ДП к коротковолновому. В первом случае размеры резонатора сравнимы с размерами электродов ДП, а длина волны, соответствующая резонансу, превышает размеры электродов. При этом возбуждение резонатора переходом осуществляется через локализованные ёмкости в местах перекрытия резонатора с электродами ДП. В случае малости этих ёмкостей резонатор можно рассматривать в виде последовательного RLC контура, соединённого параллельно ДП. Во втором случае элементам эквивалентной схемы нельзя поставить в однозначное соответствие конкретные физические объекты. Резонатор возбуждается через распределённую ёмкость, которая сравнима или превосходит ёмкость резонатора.

Работа выполнена при финансовой поддержке Российского научного фонда (Грант № 14-19-01164).

 

Литература

1.     Yu N., Capasso F. Flat optics with designer metasurfaces. // Nature Materials V. 13, P. 139–150, 2014.

2.     Yu N., Genevet P., Aieta F., et al. Flat optics: Controlling wavefronts with optical antenna metasurfaces. // IEEE J. Sel. Top. Quant. Electron. V. 19,P. 4700423, 2013.

3.  Yu N, Aieta F., Genevet P., et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces // Nano Lett. V. 12, P. 6328–6333, 2012.

4.     James J., A Student's Guide to Fourier Transforms // New York: Cambridge University Press, 2011.

5.     Hammler J., Gallant A., Balocco. Simple de-embedding and simulation technique to find permittivity with a THz vector network analyser // In Proceedings of IRMMW-THz 2015 in Hong Kong, August 23-28, 2015.

6.     Divin, Y., Snezhko, A., Poppe U., et al. Terahertz Applications of Hilbert-Transform Spectral Analysis // IEEE Transactions on Applied Superconductivity, V. 24, N. 4, 2014.

7.     Павловский В.В., Гундарева И.И., Волков О.Ю., и др.. Расширение частотного диапазона джозефсоновской импедансной спектроскопии. Радиотехника и электроника, Т. 58, №9, С. 977-988, 2013.

8.     Снежко А.В., Губанков В.Н. Взаимодействие бикристаллического джозефсоновского перехода с внешним планарным резонатором в субтерагерцевой области частот. // Нелинейный мир, Т. 13, №2, С. 46 – 48, 2015.

9.     Волков О.Ю., Губанков В.Н., Гундарева И.И. и др. Джозефсоновская спектрокопия для локальной диагностики планарных резонаторных систем в миллиметровом диапазоне длин волн. Радиотехника и электроника, 2015, Т 60 №9 с 1-6, 2015.

10.  Дивин Ю.Я., Губанков В.Н., Котелянский И.М. Бикристаллические джозефсоновские переходы для терагерцовой гильберт-спектроскопии. // Радиотехника и электроника, Т.48, № 10, С. 1238-1249, 2003.

11.  Павловский В. В. Моделирование электромагнитной резонансной системы с джозефсоновским переходом. // Журнал радиоэлектроники, №3. 2013. URL: http://jre.cplire.ru/jre/mar13/4/text.pdf

12.  Снежко А. В., Павловский В. В., Губанков В. Н., Покалякин В. И. Локальное измерение диэлектрических свойств материалов с помощью терагерцовой джозефсоновской спектроскопии // Журнал радиоэлектроники, №9. 2015, URL: http://jre.cplire.ru/jre/sep15/10/text.pdf