|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 1999 |
|
О ВОЗМОЖНСТИ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ВЕРХНИХ СЛОЕВ ПОДСТИЛАЮЩИХ СРЕД ПО ИЗМЕРЕННЫМ КОЭФФИЦИЕНТАМ ОТРАЖЕНИЯ ПРИ НАКЛОННОМ ЗОНДИРОВАНИИ ПЛОСКИМИ ВОЛНАМИ ВЕРТИКАЛЬНОЙ И ГОРИЗОНТАЛЬНОЙ ПОЛЯРИЗАЦИИ В СВЧ ДИАПАЗОНЕ
А.С. Шостак,
В.В. Загоскин, С.П. Лукьянов, А.С. КараушПолучена 27 октября 1999 г.
В работе анализируются особенности поведения коэффициентов отражения плоских волн вертикальной и горизонтальной поляризации при наклонном падении на контролируемую среду. Исследуется возможность совместного использования результатов зондирования вертикально и горизонтально поляризованных волн для определения электрофизических свойств верхних слоев подстилающих сред. Предлагается один из возможных составов измерительной СВЧ установки, позволяющей по результатам измерения сигналов вертикальной и горизонтальной поляризаций определять диэлектрические параметры и толщины слоистых подстилающих сред.
Работа систем радиофизической диагностики и контроля подповерхностных сред, таких как: дорожные и аэродромные покрытия, оползневые структуры, почво-грунты и шахтные разрезы, основана на анализе реакции исследуемой среды на зондирующий сигнал.
При разработке методов интерпретации данных зондирования одной из наиболее актуальных является задача адекватного описания взаимодействия электромагнитных волн с зондируемой средой, характеризуемой комплексной диэлектрической проницаемостью (e
*). Это связано с тем, что зондируемые материальные среды, а также строительные материалы, представляют собой сложные диэлектрические структуры. В реальных природных условиях эти среды постоянно контактируют с переменным температурным полем и водой в различных ее агрегатных состояниях. Эти переменные компоненты и определяют в основном диэлектрические свойства таких сред [1] .При решении задач радиоволновой диагностики состояния и свойств таких сред необходимо учитывать пространственное распределение
e*. Данные о профильном распределении e* можно получить либо из априорных данных, либо используя приближенные теоретические модели [2, 3, 4] , либо экспериментально. Одно из направлений совершенствования методов интерпретации отраженных сигналов связано с решением модельных задач, учитывающих взаимодействие плоских волн со слоистой средой, которая описывается реальными геометрическими параметрами и реальными диэлектрическими характеристиками.В данной работе анализируется поведение коэффициента отражения плоских волн вертикальной и горизонтальной поляризации при наклонном падении на контролируемую среду. Совместное использование результатов зондирования вертикально и горизонтально поляризованных волн позволяет извлекать информацию о диэлектрических свойствах зондируемых слоёв.
В настоящее время известны методы и аппаратура измерения диэлектрических параметров верхних слоев подповерхностных сред
[1]. Предлагаемый метод определения толщин и диэлектрических параметров слоистых сред,таких как почво-грунты, строительных материалов и т.д. может расширить возможности уже известных методов.Постановка задачи. На слоисто-неоднородную диэлектрическую среду из свободного пространства (e
* =1, m*=1) падает плоская электромагнитная волна под различными Q углами (Рис.1) . Требуется определить значения коэффициента отражения ( Rотр.) от исследуемой среды в зависимости от угла падения волн горизонтальной и вертикальной поляризации в случае нахождения на поверхности среды диэлектрических слоёв. Верхний слой и подстилающая среда имеют полубесконечные толщины, а толщина второго сравнительно тонкого слоя переменная величина и соизмерима с длиной волны. Значения e* второго слоя и подстилающей среды (третьего слоя) изменяются в ходе эксперимента.Рис. 1. Геометрия задачи. Вертикальная–E0 и горизонтальная–H0 поляризации.
Физическая модель.
Для проведения численного моделирования среда с профильным распределением e* обычно представляется в виде многослойной системы [4] . В этом случае e* будет функцией координаты Z , причём на границах между слоями эта функция может быть разрывной. Зависимость e*(Z) внутри каждого слоя задается численными значениями в некоторых точках Z i. Для упрощения вычислений полагаем e* между точками Z i и Z i+ 1 постоянной и однородной в C и U направлениях по слоям.Математическая модель
. Известно [5], что коэффициент отражения многослойной среды определяется по рекуррентной формуле:|
где |
(1) |
|
|
(2) |
|
где |
(3) |
Используя формулы (1-3), найдем формулы для коэффициента отражения
R1-3 в случае принятой нами модели исследования:тогда для горизонтальной поляризации [6]
:а для вертикальной поляризации [6]
:По формулам (
4- 6) для разных состояний среды были рассчитаны модули коэффициентов отражения для волн горизонтальной | Rг| и вертикальной | Rв| поляризаций при различных углах падения Q на зондируемую среду (Рис. 1). При этом варьировалась толщина тонкого слоя h2, задавались различные значения e* тонкого слоя и подстилающей среды. Для наглядности толщина тонкого слоя задавалась в относительных единицах и нормировалась при этом к длине волны в среде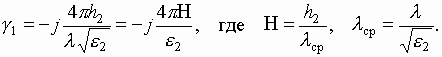
По результатам численных расчётов были построены графики модулей коэффициентов отражения для волн горизонтальной | Rг| и вертикальной | Rв| поляризаций (Рис. 2-5) в зависимости от изменения угла падения волны в пределах от 0 до 90 градусов, задания относительной толщины тонкого слоя Н от 0 до 0,5 и варьирования значений e* тонкого слоя и подстилающей среды.
Анализ формул (4-6) и графиков на Рис. 2-5 показывает, что коэффициенты отражения | Rв| и | Rг| на Рис. 2, 3 ведут себя классически, как в случае падения плоской волны на однородную диэлектрическую среду. Графики | Rг| монотонно растут от минимального значения при Q = 0 до максимального - при Q =90. Зависимость | Rв| от угла падения имеет более сложный вид. Вначале координат графики монотонно убывают до нуля, а затем более резко возрастают до единицы. Положение минимума на графике зависит от толщины и e* тонкого слоя, а также e* подстилающей среды (Рис. 2, 3). Кроме этого, наблюдается совпадение графиков | Rв| и | Rг| , полученных в случае отсутствия тонкого слоя, с графиками, когда толщина тонкого слоя равна 0,5l e (Рис. 2-5). Этот факт объясняется тем, что отраженные волны от тонкого слоя и среды суммируются в фазе.
В определенных ситуациях поведение графиков | Rв| и | Rг| отличается от рассмотренного выше (Рис. 4, 5). При определенных значениях e 1 , e 2 , e 3 слоёв и толщине тонкого слоя равной 0,25l e отраженные волны от верхнего слоя и подстилающей поверхности суммируются в противофазе, что и приводит к изменению вида графиков | Rв| и | Rг| . График | Rг| (Рис. 4(3)) ведет себя как графики | Rв| на Рис. 2, 3, при этом наблюдается провал до нуля, если имеют место слои без потерь, и отличен от нуля для сред с потерями. График | Rв| на Рис. 4, 5 повторяет ход графиков | Rг| на Рис. 2, 3. Величина коэффициентов | Rв| и | Rг| при нормальном падении волны на поверхность определяется соотношением e 1, e 2 , e 3 слоёв, при этом равенство нулю | Rв| и | Rг| при Q = 0 наблюдается, когда выполняется условие e 2 = Ö e 1 e 3 (Рис. 5 (3,6)).
Для наглядности поведения коэффициентов отражения | Rв| и | Rг| . от угла падения Q и толщины тонкого слоя Н построены трехмерные графики Рис. 6 - 11. Анализ рисунков подтверждает наличие характерных провалов на графиках | Rв| и | Rг| , которые появляются при определенных соотношениях e 1 , e 2 , e 3 слоёв, угла падения Q и толщины тонкого слоя Н. Глубина провалов на графиках зависит от наличия потерь в среде и тонком слое. Факт наличия особых точек в поведении коэффициентов отражения | Rв| и | Rг| можно использовать для разработки алгоритмов определения e* или толщины тонкого слоя.
Риc. 2. Зависимость модуля коэффициента отражения горизонтальной поляризации - |Rг| и вертикальной поляризации -|Rв| от угла падения при различных толщинах слоя –H.
Рис. 3. Зависимость модуля коэффициента отражения горизонтальной поляризации
- |Rг| и вертикальной поляризации -|Rв| от угла падения при различных толщинах тонкого слоя –H.Рис. 4. Зависимость модуля коэффициента отражения горизонтальной поляризации - |Rг| и вертикальной поляризации -|Rв| от угла падения при различных толщинах тонкого слоя –H.
Рис. 5. Зависимость модуля коэффициента отражения горизонтальной поляризации - |Rг| и вертикальной поляризации -|Rв| от угла падения при различных толщинах тонкого слоя –H.
Рис. 6. Зависимость |Rв| от угла падения Q (0..900) и толщины слоя H/100;
Изменяется |Rв| в пределах от 0 до 1e
1=1; e 2=9-j0.1; e 3=20-j0,1.Рис. 7. Зависимость
|Rв| от угла падения Q (0..900) и толщины слоя H/100;Изменяется |Rв| в пределах от 0 до 1e
1=1; e 2=3-j0.1; e 3=81-j1.Рис. 8. Зависимость |Rв| от угла падения Q (0..900) и толщины слоя H/100 (0..50);
Изменяется |Rв| в пределах от 0 до 1. e*1=1; e*2=9-j0.1; e*3=3-j0.01.
Рис. 9. Зависимость |Rг| от угла падения Q (0..900) и толщины слоя H/100 (0..50);
Изменяется |Rг| от 0 до 1. e *1=1; e *2=3-j0.1; e *3=81-j0.1.
Рис. 10. Зависимость |Rг| от угла падения Q (0..900) и толщины слоя H/100 (0..50);
Изменяется |Rг| от 0 до 1. e *1=1; e *2=9-j0.1; e *3=3-j0.01.
Рис. 11. Завмсимость |R г| от угла падения Q
(0..900) и толщины слоя H/100 (0..50).Изменяется
|R г| от 0 до50. e *1=1; e *2=9-j0.1; e *2=20-j0.1. По (4-6) были найдены координаты минимумов коэффициентов отражения |Rв| (Рис. 12) и |Rг| (Рис. 13) для фиксированных значений e 2 тонкого слоя в зависимости от e 3 среды и угла падения волны Q . Совпадающие графики 1.2 на Рис. 12 показывают зависимость минимума |Rв| от e 3 и угла падения волны Q для случая: . e 2 =9-j0,01; Н=0; и Н=0,5. График 1 построен по формулам (4, 6), а график 2 по найденной эмпирической формуле
Совпадающие графики 3,4 на Рис. 12 показывают зависимость минимума |Rв| от e 3 и угла падения волны Q для случая:. e 2 =9-j0,01; Н=0,25. График 3 построен по формулам (4, 6), а график 4 по найденной эмпирической формуле
Анализ Рис. 12 показывает, что пересечение графиков 1, 2 наблюдается при выполнении условия e 2 = e 3 –это случай однослойной среды.
График на Рис. 13 построен по формулам (4, 5). и показывают зависимость минимума |Rг| от e 3 и угла падения волны Q для случая: e 2 =3-j0,01; Н=0,25. Значение |Rг| при Q =0 определяется соотношением e 1 , e 2 , e 3 , при этом минимальное значение достигается при выполнении следующего условия (Рис. 5)
![]()
Дальнейшее увеличение e 3 (e 2 = const)приводит к смещению провала на графике в сторону больших углов падения (Рис. 4): так при e 2 =3 и e 3 =81 (вода) Q равен 84, а когда e 3 принимает значения металла, то Q равен 87,3 (Рис. 13).
Рассчитанные данные зависимостей |Rг| от e 3 для случаев Н=0,5 и Н=0,25 . по (4, 5) при e 2 =3-j0,01 приведены в таблице.
Таблица.
Значения |Rг| в зависимости от e
3
для случаев Н=0,5 и Н=0,25 при e
2 =3-j0,01.
|
e 3 |
80 |
60 |
50 |
40 |
30 |
20 |
10 |
8 |
6 |
4 |
3 |
2 |
1 |
|
|
|R г| |
,25l |
,5 |
0,44 |
0,4 |
,35 |
,28 |
0,2 |
,04 |
,045 |
0,1 |
0,2 |
,27 |
,36 |
,48 |
|
|R г| |
0,5l |
,8 |
0,76 |
,74 |
,72 |
,69 |
,64 |
,53 |
,47 |
,43 |
,35 |
,29 |
,23 |
,22 |
Выводы
. Результаты проведенных модельных расчетов позволяют сделать вывод о возможности контроля параметров слоистых сред с помощью электромагнитных волн вертикальной и горизонтальной поляризаций в СВЧ диапозоне. Методика нахождения параметров среды предполагает измерение коэффициентов |Rв| и |Rг| путём сканирования частоты генератора при различных углах падения волны на поверхность.Рис. 12. Положение провалов в графиках |Rв| на оси Q (Рис. 2-5) в зависимости от e 3 среды для различных толщин тонкого слоя – H.
Рис. 13. Положение провалов в графиках
|Rг| на оси Q (Рис. 2-5) в зависимости от e 3 среды при Н=0,25. Для случая металла под слоем наблюдается провал |Rг| при угле падения волны 87 градусов.Затем по графикам находятся особые точки и определяются их координаты - значения коэффициентов отражения |Rв|, |Rг| и углы падения волн. При этом коэффициенты отражения |Rв|, |Rг| равны нулю, когда имеет место среда без потерь, и отличны от нуля - в случае среды с потерями. Используя измеренные параметры и априорно известные находят по формулам (4-6) или (7, 8) неизвестные параметры. В качестве контролируемых параметров могут выступать диэлектрические проницаемости слоёв и среды, либо толщина тонкого слоя.
Заключение. Для определения границ практического использования результатов модельных исследований авторы продолжат работу в следующих направлениях. Предполагается создать измерительную установку, состоящую из генератора с перестраиваемой частотой, излучающей и приемной антенны, измерительного приёмника и поворотно-подьемного устройства для задания необходимых углов падения волны на поверхность среды. Будут разработаны методики определения диэлектрических параметров и толщин по результатам измерений сигналов вертикальной и горизонтальной поляризаций.Литература
1. Шутко А.М. СВЧ - радиометрия водной поверхности и почвогрунтов. -М.: Наука, 1986. 190 c.
2. Загоскин. В.В., Катаев С.Г., Тюльков Г.И., Чернышов В.Н. Исследование динамики пространственного распределения влажности, температуры и диэлектрических характеристик в капиллярно-пористых средах.- Изв. вузов. Физика, 1994. N11. - C. 10.
3. Загоскин В.В., Катаев С.Г., Тюльков Г.И., Чернышов В.Н. Влияние тепловлажностных факторов на пространственное распределение диэлектрических характеристик в капиллярно-пористых средах с проводящим компонентом на сверхвысоких частотах. - Изв. вузов. Физика, 1996, N10. -
C.50.4. Загоскин В.В., Шостак А.C., Лукьянов C.П. Влияние профильных распределений диэлектрических характеристик почво-грунтов и тонких слоёв сред на коэффициент отражения при зондировании плоскими горизонтально поляризованными волнами в СВЧ диапазоне. - "Журнал радиоэлектроники"(электронный журнал), 1999, N8.
. Козулин Ю.Н. Изв. АН СССР, сер.геофиз., 1960, стр. 1204.6. Бреховский Л.М. Волны в слоистых средах. –М.: Изд. АН СССР, 1956.
|
|
|