МОДИФИЦИРОВАННАЯ СИСТЕМА С ХАОТИЧЕСКИМ КОДИРОВАНИЕМ (CSK-СИСТЕМА) С ИСПОЛЬЗОВАНИЕМ ДИСКРИМИНАНТНОЙ ПРОЦЕДУРЫ ОБРАБОТКИ СИГНАЛОВ

А.Г. Морозов ¹ , М.В. Капранов ¹ , О.Я. Бутковский ² , Ю.А. Кравцов ³

¹  Московский энергетический институт (Технический Университет)
² Владимирский государственный университет
³ Институт космических исследований Российской Академии Наук и Центр космических исследований Польской Академии Наук

  Получена 6 октября 2000 г.

Предлагается следящая дискриминантная процедура восстановления изменений управляющего параметра нелинейного отображения непосредственно из наблюдаемой хаотической цифровой последовательности. Следящий дискриминатор, реализующий такую процедуру, допускает значительные (до 30%)  изменения управляющего параметра, что существенно превышает динамический диапазон  известных систем скрытой передачи информации с использованием хаотических сигналов. Показано, что следящий дискриминатор способен выявлять как медленную, так и быструю составляющие переменного управляющего параметра. Рассмотрена возможность реализации следящего дискриминатора в режиме реального времени.

1. Введение 

В настоящее время значительное внимание уделяется системам связи, использующим хаотические колебания и хаотические последовательности в качестве несущих (поднесущих). Основное достоинство таких систем состоит в их повышенной скрытности, которая обеспечивается как слабой предсказуемостью хаотических колебаний, так и их широкополосностью, позволяющей осуществлять передачу информации при малом (меньше единицы) отношении сигнал/шум (см. обзорные работы [1-6]). Простота реализации терминалов, возможность быстро изменять свойства приёмной и передающей сторон, широкий диапазон изменения параметров систем также относятся к достоинствам таких систем.

 Основной проблемой в реализации систем, использующих хаотические колебания в качестве переносчика информации, является демодуляция информационного сообщения. На текущий момент предложено уже много способов демодуляции хаотических колебаний, основанных на свойстве синхронизации двух и более хаотических систем с близкими параметрами, на ортогональности хаотических последовательностей, отличающихся лишь начальными условиями, на широкополосности хаотических колебаний, а также на ряде других принципов (см. обзоры [1-6]).

  Недостатками указанных систем являются крайне высокая чувствительность к неточности задания управляющих параметров (для синхронизирующихся систем и систем с разделением по начальным условиям) [7,8], к неточности задания начальных условий (для систем с разделением по начальным условиям) [9-10], невозможность восстановления информационного сообщения даже при малом уровне шумов (отношение сигнал/шум порядка 20...30 дБ), а также невозможность передачи дискретизированных по времени гладких информационных сообщений s(k) [7]. Кроме того, в ряде случаев восстановление информационного сообщения не может быть реализовано в режиме реального времени, поскольку требует значительного объёма вычислений.

Весьма перспективным методом демодуляции является использование дискриминантной процедуры, которая основана на сравнении характеристик процесса x(k) в двух соседних временных окнах. Дискриминантная процедура, разработанная первоначально для анализа нестационарности случайных процессов [11], недавно была применена для решения обратных задач хаотической динамики, т.е. для восстановления параметров динамической системы по временным реализациям, и одновременно для выявления нестационарностей в хаотических системах [12-14]. Здесь и далее термин дискриминантная процедура будет использоваться применительно к обработке хаотической последовательности, а не к описанию традиционных (частотных, фазовых и т.д.) дискриминаторов.

В данной работе в развитие публикаций [15-17] предлагаются две новые схемы восстановления информационного сообщения s(k), заложенного в изменениях управляющего параметра квадратичного отображения, на основе дискриминантной процедуры. Первая схема использует критерий статистической обработки Фишера и позволяет регистрировать (обнаруживать) скачкообразные изменения управляющего параметра. Вторая схема, использующая составляющие M₁ и M₂ (см. далее) критерия Фишера и опирающаяся на следящую дискриминантную процедуру, даёт возможность выявлять как быстрые, так и медленные изменения управляющего параметра на передающей стороне, а также оценивать величину этих изменений.

Общая схема передачи информации с использованием хаотических последовательностей представлена на  рис.1.

Рис.1. Схема передачи информации при помощи хаотических последовательностей с переменным управляющим параметром a(k).

 Пусть исходная хаотическая последовательность  генерируется отображением

                                        x(k+1)=f[a(k),x(k)],                                             (1)

 где k=0,1,2,… - дискретное время,  a(k) - управляющий параметр, зависящий от дискретного времени и несущий информационное сообщение s(k), скажем, 

                                        a(k)=a₀+Da×s(k).                                                  (2)

В случае двоичного информационного сообщения, то есть когда s(k) принимает значения 0 или 1, управляющий параметр a(k) принимает значения a₀ и a₁ºa₀+Da соответственно. Моменты перехода a(k) из состояния a₀ в состояние a₁ и обратно могут быть неизвестны на приёмной стороне.

 Попадая в канал связи, хаотическая последовательность 

                                        x(k)=x[k,a(k)],                                                        (3)

генерируемая отображением (1) с изменяющимся во времени параметром a(k), испытывает воздействие шума z(k).

Вообще говоря, непосредственная передача цифрового сигнала через среду распространения является нетипичной для современных систем связи. С целью упрощения дальнейших выкладок примем, что все преобразования, производимые над реальным сигналом (аналого-цифровые, цифроаналоговые, прохождение через зашумлённую среду распространения и т.д.) можно свести к воздействию аддитивного шума z(k) на хаотическую последовательность x(k), представленную в цифровом виде. Правила пересчёта компонент реального шума в характеристики процесса z(k) представляют собой самостоятельную задачу. В дальнейшем будем полагать, что процесс z(k) является нормальным центрированным случайным процессом с достаточно широкой полосой, чтобы считать его белым шумом для последовательности x(k).

 Тогда, в условиях наших предположений и допущений на приемное устройство поступает последовательность

                                        y(k+1)=x[k,a(k)]+z(k).                                               (4)

 Задача приемного устройства состоит в восстановлении информационного параметра a(k)  путем демодуляции зашумленной принятой последовательности y(k).

  В данной работе исследуется предложенная в работах [15-17] следящая дискриминантная процедура, которая предполагает сравнение входной цифровой последовательности y(k)=x(k)+z(k) с последовательностью z(k), которая генерируется на приемной стороне отображением f(b,z), отличающимся от исходного отображения (1) значением управляющего параметра b. В результате сравнения принимаемой последовательности y(k) с опорной последовательностью z(k), генерируемой на приёмной стороне, вырабатывается сигнал рассогласования, пропорциональный разнице d=b-a₀ между управляющими параметрами исходной и приемной нелинейных систем.  Предполагается, что исходное значение параметра b равно априорно известной с определённой точностью величине параметра a. В этом случае сигнал рассогласования может быть использован для следящей коррекции параметра b в отображении на приёмной стороне и одновременно для демодуляции информационного сообщения.

Материал расположен в следующем порядке.  Простая дискриминантная процедура, являющаяся прообразом следящего дискриминатора, описана в разд.2. В разд.3 приведены результаты применения  такой процедуры к квадратичному отображению. Разд.4 посвящен свойствам следящего дискриминатора, а разд.5 - результатам обработки сигнала при помощи следящего дискриминатора. Эти результаты свидетельствуют, в частности, о значительном (до 30%) динамическом диапазоне дискриминатора по управляющему параметру, а также о способности дискриминатора выявлять как медленные, так и быстрые вариации параметра a(k). 

2. Простая дискриминантная процедура с использованием опорной хаотической последовательности, генерируемой на приемном конце 

При использовании дискриминантного анализа для анализа случайных временных рядов сравнивают средние значения (M₁ и M₂) и дисперсии ( и ) дискриминантной (т.е. анализируемой) функции d(n) в двух соседних временных окнах (k,k-N+1) и (k-N,k-2N+1), где N - длительность каждого из окон: 

                                             (5)

                           (6)

  Различие между значениями дискриминантной  функции в двух соседних окнах удобно регистрировать, наблюдая за разностью M₁(k)-M₂(k) или же за её нормированным значением: 

                                                                                           (7)

 которое получило название критерия Фишера.

При использовании стандартного дискриминантного анализа [7] для выявления нестационарностей в случайных последовательностях y(k) в качестве дискриминантной функции была выбрана линейная авторегрессионная модель: , где q_i – коэффициенты линейной авторегрессионной модели. Иными словами, в качестве признаков события (изменение параметра) в момент дискретного времени k берутся сами наблюдаемые значения последовательности y(k). Как показывает численное моделирование, в том числе и наши собственные численные результаты, линейный дискриминантный анализ, примененный к хаотическим последовательностям с переменными во времени управляющими параметрами, не способен сколь-нибудь надежно выделить модуляцию этих параметров, что заставило искать иные способы демодуляции скрытой информации.

В работах [12-14] в качестве дискриминантной функции d(k) было предложено использовать величину (фактически нелинейную авторегрессионную модель) 

                                        d(k)=y(k+1)-F[b_j,y(k)],                                 (8)

которая  может характеризовать степень близости наблюдаемой последовательности y(k) к исходной последовательности x(k), генерируемой отображением (1). Входящие в функцию  F[b_j,y(k)] свободные параметры b_j  (скажем, это коэффициенты степенного разложения), можно найти; из условия наилучшей подгонки функции F к наблюдаемой последовательности y(k) (в смысле минимизации среднего квадрата дискриминантной функции d(k) во временном окне с одновременной максимизацией критерия Фишера H(k); эти требования составляют так называемый минимаксный критерий Фишера).

Описанный подход позволяет не только восстанавливать параметры исходной динамической системы, но и выявлять модуляцию управляющего параметра, как это было продемонстрировано в работах [12-14]  на ряде примеров, в частности, на примере последовательности, генерируемой модулированным логистическим отображением. Выбор в качестве регистрирующего критерия Фишера и линейной дискриминантной функции был продиктован наличием аналитического решения [18] и, следовательно, возможностью построения компьютерных алгоритмов, работающих в реальном времени.

Между тем, при построении дискриминатора, вычислительную задачу можно ещё более упростить, поскольку решается задача с известной структурой модели на приёмном конце, а не задача “черного ящика”. В этом случае можно предложить весьма простую процедуру выделения модуляции [15-17], при которой наблюдаемая последовательность y(k) сравнивается с последовательностью z(k),  генерируемой на приемной стороне отображением 

                                        z(k+1)=f[b,y(k)],                                              (9)

отличающимся от (1) значением управляющего параметра (b вместо a(k)). В результате, последовательность z(k) представляет собой результат вычисления отображения (9) от входной аддитивной смеси исходной последовательности x(k) и шума z(k). В качестве дискриминантной функции  d(k) предлагается использовать разность 

                                   d(k)= y(k)-z(k)                                                          (10) 

между принимаемой, y(k), и опорной, z(k), последовательностями. Такая процедура сравнения последовательностей y(k) и z(k) реализуется при помощи весьма простых элементов, как это показано на рис.2.

Рис.2 Структурная схема дискриминатора на основе критерия Фишера и дискриминантной функции d(k) вида (10).

Структурная схема дискриминатора, представленная на рис.2, напоминает систему типа Chaotic Shift Keying (CSK, т.е. хаотическое кодирование), свойства которой описаны, например, в работах [2-5], но не сводится к CSK, так как основана на иной, а именно дискриминантной процедуре обработки сигнала. В соответствии с этой процедурой решение о приеме двоичного сигнала принимается путем сравнения дискриминантного критерия Фишера (7) с порогом, тогда как в системе CSK регистрация двоичных скачков осуществляется при помощи гораздо менее эффективной процедуры, а именно, путем измерения среднего квадрата разности y(k)-z(k) и сравнения его с пороговым значением.

Указанное усовершенствование процедуры обработки выходной величины y(k)-z(k) оборачивается важными достоинствами. Во-первых, дискриминантная процедура оказывается работоспособной при значительных (до 30%) отклонениях "приемного" управляющего параметра b от управляющего параметра a в исходной системе на передающем конце. Во-вторых, по величине критерия Фишера (7) величина рассогласования между параметрами a и b оценивается с большей точностью, нежели это допускает пороговая процедура, используемая в системе CSK. В-третьих, дискриминантная процедура пригодна не только для регистрации скачков управляющего параметра a, но и для выявления иных нестационарностей  в  передающей системе.

Наконец, предлагаемая схема допускает использование более сложных, чем (10), дискриминантных функций, скажем, функций вида (8), которые зависят от нескольких управляющих параметров b_j  и тем самым делают возможной многоканальную передачу информации.  

3. Использование дискриминантной процедуры для выделения скачка управляющего параметра в квадратичном отображении 

Рассмотрим достоинства предлагаемой процедуры на примере  квадратичного отображения. Квадратичное отображение 

                               f(a,x)=1-ax²,                                                         (11)

характеризуемое единственным управляющим параметром a,  генерирует хаотическую последовательность при a>1,4. В наших расчетах значение a=a₀ было принято равным 1,6. Соответствующее отображение, генерируемое на приемном конце, имеет вид 

                              f(b,z)=1 - bz².                                                        (12)

Рис.3. Исходная хаотическая последовательность x(k), генерируемая квадратичным отображением (б), составляющие критерия Фишера  M_1,2 (k) (в) и   (г) и критерий Фишера H(k) (д) в случае скачкообразного изменения управляющего параметра a(k) в пределах от значения a₀=b=1,6 до значения a₁=1,7 (а). Длительность  окна N=10.

На рис.3 представлены результаты вычисления критерия Фишера (7),  а также параметров M_1,2  и    в условиях, когда параметр a скачкообразно менялся от значения a₀=1,6 до значения a₁=1,7 в момент времени k₁=150, а затем возвращался к первоначальному значению a₁ при k₂=350. Длительность временных окон N была выбрана равной  10: N=10.

Временная реализация параметра a(k) показана на рис.3а, а временная реализация исходной хаотической последовательности – на рис.3б. В реализации x(k) скачкообразные изменения параметра a не обнаруживаются ни визуально, ни при помощи измерения среднего значения величины x(k) или её дисперсии. Между тем, средние значения M_1,2 (рис.3в) и дисперсии  (рис.3г), равно как и критерий Фишера H(k) (рис.3д) демонстрируют отчетливые изменения в окрестности моментов скачка k₁ и  k₂. 

Согласно рис.3д, критерий Фишера H(k) реагирует на скачок управляющего параметра Da=a₁-a₀=0,1 всплеском высотой  порядка единицы и длительностью Dk~14 отсчётов дискретного времени (по уровню 0,1), сравнимой с длительностью временных окон N=10. Важно, что момент скачка регистрируется дискриминантной процедурой даже в условиях, когда разница d=b-a₀  достигает 30%. Для сравнения укажем, что аналогичный показатель для схем с синхронизацией и с разделением по начальным условиям составляет всего лишь 0,5%, а точность задания начальных условий вплоть до 10^-11 [9-10]. Таким образом, простая дискриминантная процедура налагает гораздо менее жёсткие требования на близость параметров передающей и приемной нелинейных систем, чем другие системы демодуляции.

Решение об обнаружении сигнала выносится, как и во многих задачах подобного типа, по пороговому критерию:  H_max>H_порог, где пороговое значение H_порог выбирается из условия компромисса между требованиями правильного обнаружения и минимизации ложной тревоги.

  Отклик H(k) на рис.3д отвечает отсутствию шумов в канале связи. Аддитивный шум в среде распространения z(k) приводит к некоторому снижению высоты и некоторому уширению отклика H(k).  Эта особенность иллюстрируется на рис.4., на котором показана зависимость отклика H(k) от  параметра рассогласования  d=b-a₀ при воздействии дельта-коррелированного шума z(i): 

                              <z(i)z(j)>=s²d_ij                                                    (13)

где d_ij - символ Кронеккера. Поскольку последовательность x(k) принимает значения, лежащие в пределах интервала (0;1), величина 1/s² пропорциональна отношению , которое играет роль отношения сигнал/шум в среде.

Рис.4. Отклик критерия Фишера на скачок управляющего параметра в зависимости от рассогласования  d=b-a₀ между управляющими параметрами передающей и приемной систем при различных уровнях шума: кривая 1 - s²=10^-12, кривая 2 - s²=10^-3, кривая 3 - s² =10^-2. 

Согласно рис.4, высота пика снижается с H_max=2,54 при дисперсии шума s²=10^-12 до H_max=2.43 при s²=10^-3 и до  H_max=1.59 при s²=10^-2. Кроме того, увеличивается ширина избирательной кривой max{H(k)}, рассматриваемой как функции рассогласования d =b-a₀ (с d=0.2 при s²=10^-12 до d=0.4 при s² =10^-2). Во всех случаях было использовано значение возмущения Da=0,1. Следует отметить, что возмущение Da=0,02 приводило практически к идентичным рис.4 значениям критерия Фишера.

Как показывают численные эксперименты, восстановление бинарных изменений управляющего параметра может быть зафиксировано критерием Фишера при отношении сигнал/шум порядка 17 дБ.

Исследование различных составляющих критерия Фишера показало, что составляющая M₂ практически линейно зависит от рассогласования d=b-a₀ между управляющими параметрами  передающей и приемной систем в весьма широком диапазоне значений от d=-0,3 до d=0,3 при различных уровнях шума (рис.5 а-в). Таким образом, при среднем значении a=1,6 линейная зависимость M₂ от d наблюдается при 30%-ном изменении параметров a или b.

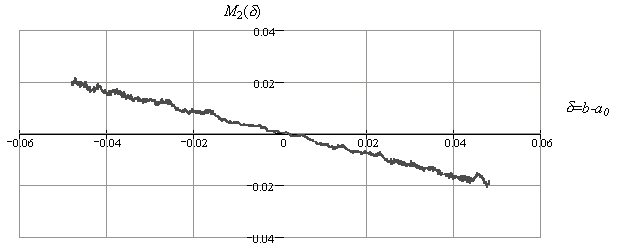
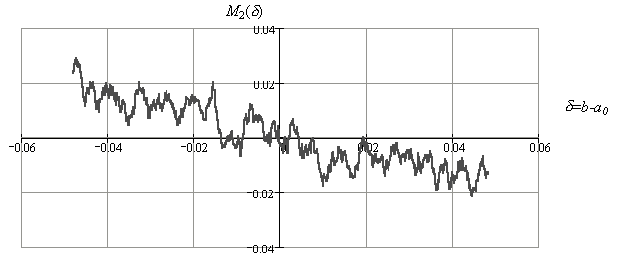
Рис.5. Зависимость составляющей M₂ критерия Фишера от разности  d=b-a₀ между значениями управляющих параметров передающей и приемной систем для квадратичного отображения (1) (центральное значение параметра a принятого равным 1,6). 

Почти линейная зависимость величины M₂ от рассогласования d между управляющими параметрами была выявлена в работах [15-17]. Такая зависимость дает ключ к эффективной демодуляции  сигнала на приемной стороне по простому алгоритму 

                                        d(k)=RM₂(k),

и открывает путь к созданию следящих дискриминантных детекторов (см. следующий раздел).

Одним из недостатков предложенной схемы является неполное использование полосы пропускания в канале связи. Действительно, минимальный период следования двоичных изменений управляющего параметра, которые ещё можно зафиксировать с использованием критерия Фишера, в безразмерных величинах составляет примерно 2N тактов каждый длительностью t. Если последовательность x(k) передаётся через цифровой тракт с многопозиционными сигналами, причём число позиций сигнала совпадает с разрядностью используемого сигнала (например, 8 разрядов двоичного представления колебания x(k) соответствуют 8 разрядам многопозиционного сигнала), то допустимое число изменений сообщения s(k) в единицу времени будет как минимум в 2N раз меньше, чем предоставленная в канале связи полоса. Использование сигнала с 8-ю позициями в большинстве случаев допустимо при хорошем отношении сигнал/шум в среде распространения. В реальных системах связи, например, в спутниковых, преимущественно используются 2х-4х позиционные сигналы. В этом случае эффективность использования предоставленного ресурса снижается ещё вчетверо или вдвое.

Возможна передача последовательности x(k) путём обработки сигнала сначала в цифроаналоговом преобразователе, с последующей фильтрацией и переносом сигнала на высокую частоту. В этом случае на приёмной стороне сначала должна выполняться обратная процедура: фильтрация – обратный перенос частоты – аналого-цифровое преобразование, с последующей обработкой, например, в соответствии с критерием Фишера. Очевидно, полоса в частотной области Dw, занимаемая последовательностью x(k), обратно пропорциональна длительности такта t, то допустимая частота W изменений двоичного сигнала s(k), передаваемого внутри последовательности x(k),  равна W=Dw /2N. Уменьшение допустимой информационной скорости передачи сообщения s(k) по сравнению с реальной скоростью передачи отсчётов последовательности x(k) вызвано тем, что для регистрации при помощи критерия Фишера каждого из скачкообразных изменений параметра необходимо около 2N отсчётов, и является своего рода платой за скрытность передачи информации. 

4. Дискриминатор с цепью регулирования управляющего параметра 

Почти линейная зависимость величины M₂ от рассогласования d=b-a₀ в сочетании с локализованным откликом критерия Фишера H(k) на  скачок управляющего параметра передающей системы позволяют реализовать дискриминатор с цепью регулирования управляющего параметра b приемной системы.  

Структурная схема такого дискриминатора, предложенная  в работе [15], приведена на рис.6. Эта схема предполагает формирование величины  :

                                                            (14)

Здесь L – интервал усреднения дискриминантной функции d(k)=z(k)-y(k), отличный от длительности окна N в простой дискриминантной процедуре и критерии Фишера (7). Крутизна q характеристики  (см. рис.5), определяется конкретным видом отображения. Отметим, что второе уравнение в системе (14) относится к установившемуся режиму, когда все переходные процессы уже завершились. Длительность переходных процессов для подобных систем, как правило, пропорциональна времени усреднения L.

В силу практически линейной зависимости величины  от рассогласования d=b-a₀ (второе уравнение в системе (14)) её можно использовать для коррекции параметра b в приемном генераторе хаотической последовательности z(k). В этом случае мгновенное значение параметра b, а значит, и мгновенное рассогласование d приобретают зависимость от дискретного времени k: 

b(k) = b₀ + Db(k) ,                                                  (15а)

d(k) = d₀ + Dd(k) ,                                                      (15б)

где b₀ и d₀=b₀-a₀ – значения параметров в отсутствие корректирующей цепи.  Математически корректирующая цепь (рис.6) описывается выражением:           

,                                 (16а)

 или, с учётом второго уравнения (14), а также уравнений (15а) и (15б) в установившемся режиме:

                                                   (16б)

откуда имеем значение ошибки слежения в установившемся режиме: 

.                                                          (16в)

Если использовать сумму b₀+Db(k) в качестве оценки значения параметра a(k), то модуль коэффициента R должна быть максимальным, чтобы удовлетворить условию минимизации установившейся ошибки d_уст (16в), то есть, максимального совпадения мгновенного значения суммы b₀+Db(k) со значением параметра a(k).

В то же время, как показывают численные эксперименты, увеличение модуля коэффициента R выше некоторого значения R_max приводит к возникновению автоколебаний в контуре обратной связи.

Таким образом, при условии минимизации ошибки слежения величина коэффициента выбирается максимально возможной, при которой ещё не возникают автоколебания.

Кроме того, как показывают численные эксперименты, параметр R, аналогично коэффициенту обратной связи в системах ФАП, влияет на длительность переходного периода Dk, в течение которого величина b₀+Db(k) приходит к установившемуся значению, определяемому формулой (16в).

Не всегда необходимо знать точное значение параметра a(k), а необходимо знать лишь его вариации Da×s(k) (второе слагаемое в (2)). Тогда, в качестве оценки переменной составляющей Da×s(k) можно использовать величину  (Выход 1 на Рис.6).

Рис.6. Схема следящего дискриминатора, вырабатывающего корректирующую поправку к управляющему параметру опорного отображения.

В качестве примера на рис.7 показан отклик корректирующего сигнала d(k)=b(k)-a(k)  на прямоугольный скачок величиной  Da=0,1 управляющего параметра a передающей системы.

Рис.7. Отклик корректирующей цепи d(k) (кривая 1) на прямоугольный скачок управляющего параметра Da=a₁-a₀=0,1 (кривая 2). Период усреднения L равен 40.

 На рис.7 приведён график, отвечающий времени усреднения L=40. Видно, что корректирующий отклик  вырабатывается за времена, сравнимые с длительностью окна L=40.

Численные эксперименты показали, что следящий дискриминатор позволяет восстанавливать возмущения более сложной формы, чем прямоугольная. На рис.8 кроме исходного информационного сигнала a(k), представляющего собой биение двух гармонических сигналов (рис.8а), показано сообщение, восстановленное дискриминатором на основе критерия Фишера (использовалась компонента M₂(k)) (рис.8б) и сообщение, восстановленное при помощи следящего дискриминатора при значении параметра обратной связи R=-2 (рис.8в).  Из сравнения графиков на рис.8а,б,в видно, что следящий дискриминатор воспроизводит сигнал с меньшими искажениями (рис.8в),  чем дискриминатор на основе критерия Фишера (рис.8б).

а)

б)

в)

Рис.8. Сравнение исходного сигнала s(k) (а) c откликом компоненты M₂(k) критерия Фишера при отсутствии (б) и наличии (в) корректирующего сигнала в системе со следящим дискриминатором.

При приёме сигналов сложной формы следящий дискриминатор может быть использован в качестве сглаживающего фильтра, для чего интервал усреднения L при формировании величины  (14)  следует взять большим, чем длительность окна N.  На рис.9 показан сложный передаваемый сигнал a(k) (тонкая штриховая линия), представляющий собой сумму двух синусоидальных сигналов, один из которых имеет короткий период  Dk₁=30,  c другой - длинный период  Dk₂=500. 

Рис.9. Сглаживающее действие следящего дискриминатора при длительном времени усреднения L>>N: принимаемый сигнал (тонкая штриховая линия), компонента M₂ критерия Фишера при N=10 (толстая сплошная линия) и коррекция d(k) (тонкая сплошная линия), отвечающая величине   с периодом усреднения L=60.

Короткопериодный сигнал выделяется из компоненты M₂(k)  критерия Фишера при длительности окна  N=10 (толстая сплошная линия), тогда как длиннопериодная часть отфильтровывается из корректирующего сигнала  при интервале усреднения L=60. Таким образом, варьируя длительность окна N и длительность периода усреднения L, при помощи следящего дискриминатора можно выделять как быстрые, так и медленные компоненты сигнала  a(k).

  Еще одна особенность следящего дискриминатора заключается в его способности стабилизировать дисперсию выходного шума. На рис.10 показана серия зависимостей дисперсии  измеренной величины d(k), которая может рассматриваться как один из выходов приёмника, от дисперсии входного шума s² при различных периодах усреднения (L=20,40,60,80 и 100).

Рис.10. Зависимость дисперсии   сигнала коррекции d(k)=b(k)-a(k) от интенсивности входного шума s² при различных длительностях усреднения и L=20,40,60, 80 и 100 (в левой части рисунка соответствующие кривые идут сверху вниз). 

Рис.10 показывает, что при малых интенсивностях входного шума s² дисперсия шума на выходе  остается практически постоянной до значений s²~10^-3, что отражает следящие свойства дискриминатора. При значениях s², превышающих 10^-3, уровень выходного  шума  начинает возрастать, а при s²³3×10^-2 система вовсе утрачивает способность восстанавливать вносимые возмущения управляющего параметра a. Происходит это потому, что быстрые шумовые составляющие Db(k) почти в точности противоположны по знаку вносимым шумовым компонентами принимаемой смеси y(k). В силу почти линейной зависимости составляющей M₂ от d указанные компоненты частично компенсируются, так что при соответствующем выборе коэффициента R можно добиться практически полной компенсации малых шумов, поступающих из среды.

Пороговое отношение сигнал/шум, при котором ещё возможно восстановление информационного сигнала, в численных экспериментах оказалось равным порядка 11дБ.

Численное моделирование показало, что пропорциональность величины M₂ рассогласованию d₀=b₀-a₀, благодаря которой и становится возможной следящая дискриминация, имеет место не только для квадратичного отображения (1), но и для других гладких  отображений, например, для логистического изображения f(a,x)=ax(1-x). В случае же разрывных отображений типа  f(b,x)=ax, mod=1, а также отображений с разрывной производной (отображения типа "домика"), гладкая зависимость M₂ от d нарушается, что препятствует созданию следящих дискриминаторов на основе таких отображений. Отметим ещё, что в рабочей области изменения управляющего параметра не должно быть "окон нехаотичности", отвечающих регулярным режимам, иначе будет нарушена скрытность передачи информации. 

5. Заключение 

В данной работе предложена простая дискриминантная процедура демодуляции сигналов с хаотической несущей, основанная на сравнении принимаемой хаотической последовательности  y(k) с опорной последовательностью z(k), генерируемой в приемной системе с иным, чем в исходной системе значением управляющего параметра.

Предложенная в работе модификация CSK-система на основе критерия Фишера предполагает введение обратной связи. В отсутствие шума такой следящий дискриминатор позволяет отслеживать изменения управляющего параметра (в области хаотических режимов) в пределах 30%, что существенно (почти на два порядка величины) превышает предельные значения Da (порядка долей процента), характерные для других известных схем демодуляции хаотических  сигналов.

Предложенная схема следящего дискриминатора продемонстрировала удовлетворительное качество восстановления сигналов при отношении сигнал/шум превышающий уровень 11дб, в то время как простая (неследящая) дискриминантная процедура работоспособна при заметно более высоком отношении сигнал/шум порядка 17дБ.

Обе модификации CSK-системы позволяют восстанавливать информационные сообщения в отсутствие дополнительного канала потактовой синхронизации хаотической цифровой последовательности. Это принципиально отличает предложенные схемы со схемами с разделением информации по начальным условиям или синхронизации. Даже несмотря на то, что система с разделением по начальным условиям может демонстрировать устойчивое поведение при наличии шумов, превышающих уровень самой хаотической несущей в несколько раз, для данной схемы необходимым является наличие дополнительного канала потактовой синхронизации. В силу экспоненциально убывающей корреляционной функции хаотических цифровых последовательностей, временной сдвиг даже на один такт приведёт к полной неработоспособности подобной схемы и невозможности восстановить передаваемое сообщение на приёмной стороне.

 Данная работа осуществлялась при частичной поддержке РФФИ (грант 99-02-16625) и ФЦП "Интеграция" (грант А-0029/99).

 Литература

1.    А.С.Дмитриев, А.И.Панас, С.О.Старков. Динамический хаос как парадигма современных систем связи // Зарубежная радиоэлектроника - Успехи современной радиоэлектроники. 1997. No 10. С.4-19.

2.     M.Hasler. Synchronization of chaotic systems and transmission of information // Intern. J. of Bifurcation and Chaos. 1998. Vol.8, No.4. P 647-659.

3.    G.Kolumban, B.Vizvari, P.Schwarz and A.Abel.  Differential chaos shift keying: a robust coding for chaos communication. // Proc. NDES'96. 1996. Seville. P. 87-92.

4.     G.Kolumban, M.Kennedy, L.Chua. The role of synchronization in digital communications using chaos – Part-I: Fundamentals of digital communications // IEEE Trans. CAS 1997. Vol.44 No.10. P.927-936.

5.     G.Kolumban, M.Kennedy, L.Chua. The role of synchronization in digital communications using chaos – Part-II: Chaotic modulation and chaotic synchronization // IEEE Trans. CAS 1998. Vol.45. No.11. P.1129-1140.

6.    T.Yang, L.O.Chua Application of chaotic digital code-division multiply access (CDMA) to cable communication systems // Intern. J. of Bifurcation and Chaos, 1998. Vol.8, No.8. P.1657-1669.

7.     M.V.Kapranov, A.G.Morozov. Application of chaotic modulation for hidden data transmission // Proc. NDES'97. Moscow. P. 223-228.

8.    М.В.Капранов, А.Г.Морозов Использование хаотической модуляции для передачи информации// Радиотехнические тетради. М.:Изд. МЭИ, 1998 №14.

9.     V.N.Kuleshov, M.V.Larionova, N.N.Udalov. Information transmission system using chaotic carrier: demands to the accuracy of symbols generation // Proc. 1998 International Symposium on Acoustoelectronics, Frequency Control and Signal Generation, St.-Petersburg, 1998. P. 192-199.

10. V.N.Kuleshov,  N.N. Udalov. Nonlinear filtering of modulated chaotic oscillation // Proc. NDES'97. Moscow. P. 537-542

11. Обнаружение изменений свойств сигналов и динамических систем:. Пер. с англ. Под. Ред. М.Бассвиль, А.Банвениста.-М.: Мир, 1989.-278с.

12. O.L.Anosov, O.Ya.Butkovskii, Yu.A.Kravtsov, et.al. Dynamic equation reconstruction from the observed one-dimensional time series. / In book: Dynamical Systems and Chaos. (Y.Aizawa, S.Saito, K.Shiraiwa, Eds.) 1994. World Scientific, Sigapore, Vol. 2, P.378-380.

13. О.Л.Аносов, О.Я.Бутковский, В.В.Исакевич, Ю.А.Кравцов. Выявление нестационарных участков при помощи нелинейной модели процесса. // Радиотехника и электроника. 1995, Том 40, No 2, С.255-260.

14. O.L.Anosov, O.Ya.Butkovsrii. A Discriminant Procedure for the Solution of Inverse Problems for Non-stationary Systems. / In book: Predictability of Complex Dynamical Systems (Yu.A.Kravtsov, J.B.Kadtke Eds). 1996. Springer Verlag, Berlin, Heidelberg, p.67-78.

15. M.V.Kapranov, A.G.Morozov. An opportunity to reduce requirements to accuracy of chaotic signal generation by adaptive processing of digital chaotic sequence with stored information // Proc. 1998 International Symposium on Acoustoelectronics, Frequency Control and Signal Generation, St.-Petersburg. 1998. P.182-186.

16. А.Г.Морозов. Адаптивная обработка хаотических цифровых последовательностей со внесённой информацией // Радиотехнические Тетради. М.:Изд. МЭИ. 1998. №17. C.64-68.

17. A.G.Morozov. Simultaneous transmitting of several data streams within single chaotic carrier // Материалы третьей международной конференции "Перспективные технологии в средствах передачи информации – 99"., 1-5 июля 1999. Владимир. С.125-129.

18. М.Кендалл, А.Стюарт. Многомерный статистический анализ и временные ряды. М.: Наука. 1976. с.736

оглавление

дискуссия