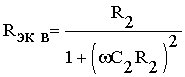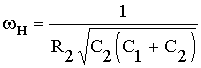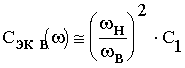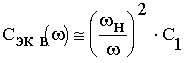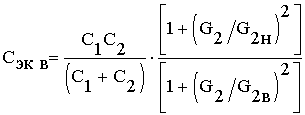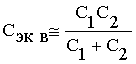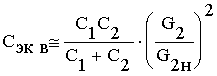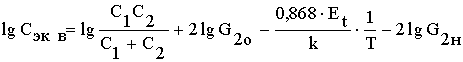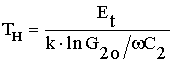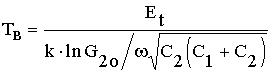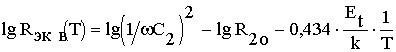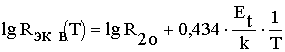"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 10, 2003

оглавление

дискуссия

 

ТЕМПЕРАТУРНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СТРУКТУР С БАРЬЕРОМ ШОТТКИ

 

 

Мамедов Азер Каграман оглы ; e-mail:   mamedov_az50@mail.ru                   

Азербайджанский Технический Университет

 

 

 

Получена 08 октября 2003 г.

 

    Разработана графоаналитическая модель структур с барьером Шоттки, аппроксимирующая реальные зависимости эквивалентной емкости и сопротивления от частоты и температуры в виде ломаной линии с несколькими изломами.

 

 

 

 

Структуры с барьером Шоттки являются неотъемлемой частью ряда элементов электроники, таких как диоды и фотодиоды Шоттки, транзисторы с затвором Шоттки и некоторых других. Анализ частотно-температурных зависимостей емкости, диэлектрических потерь и электропроводности подобных элементов [1,2] вызывает необходимость использования различного рода моделей. Поэтому вопросы, связанные с разработкой математических, графических и графоаналитических моделей структур с барьером Шоттки, представляют значительный интерес. Подобную структуру можно представить [3,4] в виде последовательного соединения емкости С₁ и сопротивления R₁ контакта с емкостью С₂ и сопротивлением R₂ объема. Чтобы результаты измерения емкости и сопротивления структуры с барьером Шоттки можно было сравнивать с теоретическими результатами необходимо указанную структуру представить в виде эквивалентных емкости С_экв и сопротивления R_экв. С этой целью воспользуемся соотношениями [2], связывающими С_экв и R_экв последовательной схемы замещения с С₁, R₁ и С₂, R₂

,                                                  (1)

.                                                                 (2)

Измерения проводятся при малых переменных напряжениях, поэтому сопротивление контакта R₁ много больше сопротивления объема R₂ и можно рассматривать упрощенную эквивалентную схему, в которой не учитывается сопротивление R₁. Указанная модель представляет собой широко используемую в практике исследований учеными разных стран классическую модель Simmonsа [3,4]. Однако построение кривых зависимости емкости и сопротивления от частоты и температуры по соотношениям (1), (2) достаточно громоздкая задача.

Целью настоящей работы является разработка наглядной графоаналитической модели, аппроксимирующей реальные кривые зависимостей эквивалентной емкости и сопротивления от частоты и температуры и позволяющей существенно облегчить задачу анализа и расчета структур с барьером Шоттки.

Рассмотрим зависимость эквивалентной емкости от частоты. Перепишем выражение (1) в виде

,                                                           (3)

где

,                                                                             (4)

.                                                           (5)

На низких частотах w<w_н, w_в

.                                                                            (6)

На высоких частотах w/w_н , w/w_в>1. Реально при w/w_н , w/w_в=2-3 единицей в числителе и в знаменателе выражения (3) можно пренебречь. Тогда это выражение можно представить в виде

.                                                            (7)

Учитывая (4), (5) из (7) для частот w>w_в, получим

.                                                                (8)

Из выражений (6) и (8) следует, что на низких w<w_н и высоких w>w_в частотах С_экв практически не зависит от частоты.

В диапазоне частот w_н<w<w_в

.                                                            (9)

Кривая, построенная по аппроксимирующему соотношению (9) в двойном логарифмическом масштабе, представляет собой прямую линию. При этом изменение частоты в 2 раза приводит к изменению емкости в 4 раза.

Таким образом, кривая, аппроксимирующая зависимость эквивалентной емкости от частоты, описывается соотношениями (6), (8), (9) и в координатах lgC_экв-lgw представляет собой ломаную прямую линию, имеющую два излома. На рис.1а представлены реальная (1) и аппроксимирующая (2) кривые, а также экспериментальные точки зависимости эквивалентной емкости от частоты, построенные в координатах lgC_экв-lgw по полученным соотношениям для структуры с С₁=1700 пФ, С₂=150 пФ. Видно, что аппроксимирующая кривая согласуется с реальной и результатами эксперимента. Погрешность аппроксимации максимальна в точках излома характеристики и составляет величину порядка 50 %. Такое же согласование наблюдалось и с результатами работ [4-6].

 

 

Рассмотрим зависимость эквивалентной емкости от температуры. Перепишем выражение (1) в виде

,                                          (10)

где

,                                                                                   (11)

.                                                                (12)

Проводимость G₂ зависит от температуры и определяется выражением

.                                                        (13)

При низких температурах G₂< G_2н, G_2в и

.                                                                          (14)

При высоких температурах G₂>G_2н,G_2в  и

.                                                                                   (15)

При температурах, для которых G_2н<G₂<G_2в

.                                                         (16)

Выражения (14)-(16) означают, что зависимость эквивалентной емкости от проводимости G₂  в двойном логарифмическом масштабе lgC_экв-lgG₂(T) хорошо аппроксимируется ломаной прямой линией, имеющей два излома.

Из (13) имеем

.                                             (17)

Подставляя (17) в (16), получим

.        (18)

Соотношение (18) означает, что аппроксимирующая кривая, построенная в координатах lgC_экв-1/T в диапазоне температур Т_н<T<T_в имеет вид спадающей прямой линии с наклоном 0,868×Е_t/k. Значения температур Т_н и Т_в соответствуют значениям проводимости G_2н и G_2в. Учитывая (11) и (12), для Т_н и Т_в  получим

 ,                                                               (19)

.                                            (20)

На рис.1б представлены реальная теоретическая (1) и аппроксимирующая (2) кривая, а также экспериментальные точки зависимости эквивалентной емкости от обратной температуры, построенные в координатах lgC_экв-1/T по соотношениям (14), (15) и (18) для структуры с С₁=1700 пФ, С₂=150 пФ при частоте f=1кГц. Видно, что аппроксимирующая кривая вполне согласуется с реальной кривой и результатами эксперимента. Погрешность аппроксимации максимальна в точке излома характеристики и составляет величину порядка 50 %. Такое же согласование наблюдалось и с результатами работ [4-6].

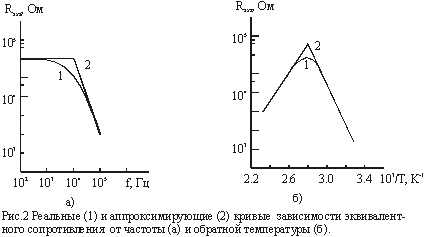
Рассмотрим зависимость эквивалентного сопротивления от частоты и температуры. Нетрудно показать, что на высоких частотах w/w_в>1 выражение (2) можно представить в виде

,                                                           (21)

а на низких частотах w/w_в<1

,                                                                         (22)

т.е. кривая, аппроксимирующая зависимость R_экв(w), описывается соотношениями (21), (22) и в двойном логарифмическом масштабе представляет собой ломаную прямую линию, имеющую один излом.

При низких температурах из выражения (2) получим

,                 (23)

а при высоких температурах

.                                       (24)

Соотношения (23), (24) означают, что кривая, аппроксимирующая зависимость R_экв(Т), построенная в координатах lgR_экв-1/T, в диапазоне температур Т>T_н имеет вид нарастающей, а в диапазоне температур Т<T_н - вид спадающей прямой линии с наклоном 0,434×E_t/k.

На рис.2 представлены реальная теоретическая (1), а также аппроксимирующая (2) кривые зависимости эквивалентного сопротивления от частоты (а) и температуры (б), построенные в координатах lgR_экв(w)-lgw и lgR_экв-1/Т, по соотношениям (2), (21)-(24) для структуры с С₁=1700 пФ,  С₂=150 пФ.

 

 

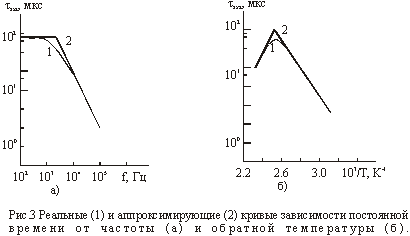
Характерным параметром, определяющим частотные и временные параметры контакта с барьером Шоттки, является постоянная времени t_экв=R_экв×C_экв. Предложенная аппроксимация удобна также потому, что пользуясь ею весьма просто построить кривые, аппроксимирующие зависимости t_экв(w) и t_экв(Т) по известным зависимостям С_экв(w), R_экв(w) и С_экв(Т), R_экв(Т). Они получаются простым сложением этих характеристик. На рис.3 представлены реальная теоретическая (1) и аппроксимирующая (2) кривые зависимости постоянной времени от частоты (а) и обратной температуры (б). Видно, что они имеют вид ломаной прямой линии, имеющей один излом.

 

 

 

литература

 

1.Симон  Ж.,  Андре   Ж.-Ж.   Молекулярные  подупроводники :  фотоэлектрические  свойства  и  солнечные  элементы. Пер. с англ., М., Мир,  1988, 344с.

2.Nowroozi-Esfahani R., Maclay G.J. Complex  impedance  measurements  of  capacitor  structures  on  silicon  with  copper  phthalocyanine  dielectric. Journal  of  Applied  Physics, 1990,  v. 67,  N7, p.3409-3418.

3.Simmons J.G. Alternating current electrical properties of highly doped insulating films. Journal  of  Applied  Physics, 1970,  v.41,  N2, p.538-544.

4.Simmons J.G., Wei L.S. Theory  of  transient  emisson  current  in  MOS  devices  and  the  direct  determination  of interface  trap  parameters. Solid  State  Electronics, 1974,  v.17,  p.117-124.

5.Barkhalov B.Sh., Y.A. Vidadi. Properties of Al /copper phthalocyanine/  Ag diode structures with Schottky barriers. Thin solid films, 1977, v.40, N2, p.15-18

6.Fernandez-Canque H.L., Allison J., Thompson M.J. The  capacitance  of  rf  sputtered  hydrogenated  amorphous  silicon,  Schottky  barrier  diodes. Journal  of  Applied  Physics, 1983,  v.54,  N12, p.7025-7033.