|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 10, 2003 |
|
Генерация квазиодномерной оптической решетки в квадратично-нелинейной среде скрещенными пучками основной частоты
А. П. Сухоруков, e-mail: aps@nls.phys.msu.su ,
Д. А. Чупраков, e-mail: chup@nls.phys.msu.su .
Московский государственный университет им. М. В. Ломоносова
Получена 29 октября 2003 г.
Изучается модуляционная неустойчивость широкого эллиптического пучка основной частоты в квадратично-нелинейной среде при начальной модуляции амплитудного профиля наклонным пучком той же частоты. Найдена область параметров (пространственных частот модуляции, амплитуды пучка и фазовой расстройки волновых векторов) для генерации решетки на выходе нелинейной среды. Найденная область образования решетки сравнивается областью положительного инкремента модуляционной неустойчивости плоской стационарной волны.
В исследованиях нелинейного распространения оптических волн всегда важен анализ их устойчивости. Сильная нелинейность может приводить к распаду волны, как во времени [1], так и в пространстве [2]. Результатом пространственной неустойчивости в нелинейной среде становится формирование разнообразных поперечных структур, в том числе периодически-регулярных. Наиболее интересным и интенсивно изучаемым механизмом генерации таких структур на протяжении уже более 30 лет является модуляционная неустойчивость пучков, впервые обнаруженная Беспаловым и Талановым в середине 60-х годов [2]. Её суть в том, что малые пространственные возмущения поля плоской волны, находящиеся в определенной ограниченной области спектра пространственных частот, усиливаются по мере распространения, и плоский фронт волны постепенно превращается в структуру маленьких субпучков. Если область неустойчивых пространственных частот достаточно узка, распадная структура имеет вид периодической решетки. Строго говоря, вид такой структуры определяется пространственным спектром начального возмущения, полем волны и параметрами среды.
Первые исследования модуляционной неустойчивости проводились в кубично-нелинейных средах с керровской нелинейностью [2-4]. Из-за сильной самофокусировки (2+1) D пучка исследователи прибегали к разным механизмам, ослабляющим её, таким как поперечная фазовая [5-10] или поляризационная [11] модуляция пучка. Лишь сравнительно позднее такие структуры начали наблюдаться в фоторефрактивных [12,13] и квадратично-нелинейных [14-16] средах. Поперечный распад нелинейных волн немало изучался теоретически в приближении малого возмущения плоских одномерных стационарных волн [17-20]. Каждая пространственная гармоника такого возмущения усиливается экспоненциально по амплитуде и решение линеаризованных уравнений относительно возмущения позволяет вывести соотношение между инкрементом неустойчивости, интенсивностью плоской волны и периодом структуры. Специальные исследования экспериментально [16] и численно [20] подтвердили экспоненциальный характер роста малого возмущения у широкого пучка в планарном волноводе. Аналогично системе (1+1) D волн, анализ модуляционной неустойчивости может быть проведен для системы (2+1) D волн.
В экспериментах на вход объемной квадратично-нелинейной среды обычно подается эллиптический пучок основной частоты, малая и большая оси которого выбираются таким образом, чтобы распад пучка при заданной интенсивности мог происходить лишь вдоль направления большой оси [14,16]. Для этого размер вдоль большой оси пучка должен в несколько раз превышать диаметр солитона для заданной интенсивности и параметров среды, а другой поперечный размер пучка следует задать не больше этого характерного размера. Может оказаться практически важным получать на выходе решетку с заданным пространственным периодом. Для этого достаточно слабо промодулировать начальный профиль пучка с требуемым периодом. Для такой цели может использоваться схема скрещенных пучков, в которой мощный пучок пересекается на входе в нелинейную среду с другим более слабым наклонным пучком. Такая схема генерации решетки пучков уже применялась Шиком, Стегеманом и Малендевичем при изучении модуляционной неустойчивости на планарном волноводе с кристаллом LiNbO3 [16]. Детальный анализ позволил сравнить значения инкремента модуляционной неустойчивости, полученные теоретически и экспериментально для системы (1+1) D пучков [20]. В настоящее время остается теоретически мало исследованной распадная неустойчивость эллиптического пучка в двумерной среде, наблюдавшаяся в экспериментах Стегемана [14]. Динамику развития неустойчивости нестационарных пучков не удается описать аналитически, и на первый план здесь выступают численные эксперименты. При исследовании поперечного распада пучков важен учет конкурирующих с модуляционной неустойчивостью нелинейных аберраций, также приводящих к разбиению пучка. В работе [21] уже анализировалось влияние взаимофокусировки и дифракции на распад двумерного гауссова пучка основной частоты, возмущенного наклонными пучками при отсутствии второй гармоники на входе, а в работе [22] рассматривалась неустойчивость такой системы при наложении гауссовых шумов, а также учете временного ограничения пучка. Немало внимания уделялось также зависимости количества субпучков в решетке от размеров и интенсивности эллиптического пучка [14,21]. Среди неизученных в настоящее время вопросов остаются определение области параметров квадратично-нелинейной среды и пучка для генерации квазиодномерной решетки, исследование распространения решетки на дальние расстояния, а а также возможность образования решетки при скрещивании пучков в глубине нелинейной среды. В настоящей работе мы аналитически и численно изучаем эти вопросы.
2. Постановка задачи и основные уравнения.
Будем рассматривать вырожденный тип трехчастотного взаимодействия,
когда в квадратично-нелинейной среде распространяются две волны на основной и
удвоенной частотах. Тогда в отсутствие поперечного сноса энергии, вызванного
двулучепреломлением в среде, нормированные комплексные огибающие ![]()
![]() пучков гармоник при распространении волн вдоль оси z описываются следующей системой нелинейных
дифференциальных уравнений типа НУШ [17]:
пучков гармоник при распространении волн вдоль оси z описываются следующей системой нелинейных
дифференциальных уравнений типа НУШ [17]:
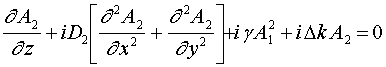 , (1б)
, (1б)
где ![]() ,
, ![]() - поперечные координаты,
- поперечные координаты,
![]() - коэффициент дифракции
пучков,
- коэффициент дифракции
пучков, ![]() - коэффициент
нелинейности,
- коэффициент
нелинейности, ![]() - расстройка
волновых векторов,
- расстройка
волновых векторов, ![]() - волновое число,
- волновое число, ![]() - круговая
частота электрического поля первой гармоники,
- круговая
частота электрического поля первой гармоники, ![]() - нелинейная восприимчивость
второго порядка,
- нелинейная восприимчивость
второго порядка, ![]() - скорость света в вакууме,
- скорость света в вакууме, ![]() - линейный
показатель преломления волны на основной частоте.
- линейный
показатель преломления волны на основной частоте.
Представим, что на границу квадратично-нелинейной среды
падает мощный гауссов пучок основной частоты с эллиптическим сечением. Под
малым углом ![]() к нему падает другой
более слабый по мощности пучок той же частоты. Вторая гармоника на входе
отсутствует. Тогда амплитудный профиль суперпозиции всех падающих на вход в
нелинейную среду волн запишется в виде:
к нему падает другой
более слабый по мощности пучок той же частоты. Вторая гармоника на входе
отсутствует. Тогда амплитудный профиль суперпозиции всех падающих на вход в
нелинейную среду волн запишется в виде:
где
![]() и
и
![]() - пиковые
амплитуды мощного и затравочного пучка соответственно,
- пиковые
амплитуды мощного и затравочного пучка соответственно,
![]() и
и
![]() - координаты
центров пучков на входе,
- координаты
центров пучков на входе,
![]() - ширина
пучков вдоль малой оси,
- ширина
пучков вдоль малой оси,
![]() - коэффициент
эллиптичности пучков,
- коэффициент
эллиптичности пучков,
![]() -
поперечная составляющая волнового вектора слабого пучка,
-
поперечная составляющая волнового вектора слабого пучка, ![]() - относительная фаза наклонного
пучка. При
- относительная фаза наклонного
пучка. При ![]() пучки
пересекаются на входе в среду, и в результате интерференции на амплитудный
профиль мощного пучка накладывается малая гармоническая модуляция с частотой
пучки
пересекаются на входе в среду, и в результате интерференции на амплитудный
профиль мощного пучка накладывается малая гармоническая модуляция с частотой ![]() ,
пропорциональной углу пересечения пучков. Из (2) при
,
пропорциональной углу пересечения пучков. Из (2) при ![]() имеем:
имеем:
где введены обозначения:
![]() ,
, ![]() . Из (3) видно, что кроме
амплитудной модуляции, наклонный пучок задает модуляцию фазового профиля с той
же самой частотой, хотя для развития модуляционной неустойчивости она не
является обязательной. Если
. Из (3) видно, что кроме
амплитудной модуляции, наклонный пучок задает модуляцию фазового профиля с той
же самой частотой, хотя для развития модуляционной неустойчивости она не
является обязательной. Если ![]() , пучки пересекаются на расстоянии
, пучки пересекаются на расстоянии
![]() .
.
Уравнения (1) решались численно методом простой итерации
с автоматическим подбором шага и использованием разностной схемы Фурье. Число
узлов по поперечной сетке составляло 512´128
для области размерами (100´40)a. При решении уравнений использовалась следующая
нормировка: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
При этом интенсивность
.
При этом интенсивность ![]() соответствует интенсивности
соответствует интенсивности
![]() для параметров кристалла
КТР [14].
для параметров кристалла
КТР [14].
3. Аналитическое описание модуляционной неустойчивости плоских стационарных волн.
Для описания развития поперечной неустойчивости
эллиптического пучка необходим анализ уравнений (1) в первом приближении теории
возмущений. Он позволил бы выявить динамику малого гармонического возмущения,
наложенного на пучок. Однако такая система оказывается слишком сложной для
аналитического описания, поэтому ограничимся рассмотрением более простой системы
плоских стационарных волн первой и второй гармоник в планарном волноводе. Их комплексные
амплитуды описываются системой уравнений (1) при отсутствии члена со второй
производной по y. Пусть на входе плоские волны слабо
возмущёны вдоль поперечной координаты ![]() , так что исходные профили пучков можно
записать в виде:
, так что исходные профили пучков можно
записать в виде:
![]() , (4)
, (4)
где ![]() и
и
![]() - амплитуда
и нелинейный сдвиг волнового числа плоской волны j-ой гармоники,
- амплитуда
и нелинейный сдвиг волнового числа плоской волны j-ой гармоники,
![]() - её
малое возмущение. Невозмущённую амплитуду
- её
малое возмущение. Невозмущённую амплитуду ![]() и сдвиг волнового числа
и сдвиг волнового числа ![]() можно легко
найти из (1) как решения стационарной задачи. Эволюция возмущения
можно легко
найти из (1) как решения стационарной задачи. Эволюция возмущения ![]() плоской
стационарной волны была подробно исследована в [18] и, как выяснилось, может
быть представлена в виде суперпозиции пространственных угловых компонент с
начальной амплитудой
плоской
стационарной волны была подробно исследована в [18] и, как выяснилось, может
быть представлена в виде суперпозиции пространственных угловых компонент с
начальной амплитудой ![]() (
(![]() ) и экспоненциальным ростом вдоль координаты
распространения z:
) и экспоненциальным ростом вдоль координаты
распространения z:
![]() . (5)
. (5)
Здесь ![]() - комплексный
инкремент неустойчивости, чья вещественная положительная часть описывает скорость
усиления угловой компоненты. Трилло и Ферро в [18] вывели аналитическое
выражение, устанавливающее взаимосвязь между инкрементом роста, частотой
возмущения и амплитудой плоской волны. Это выражение можно представить в виде
следующей неявной зависимости инкремента
- комплексный
инкремент неустойчивости, чья вещественная положительная часть описывает скорость
усиления угловой компоненты. Трилло и Ферро в [18] вывели аналитическое
выражение, устанавливающее взаимосвязь между инкрементом роста, частотой
возмущения и амплитудой плоской волны. Это выражение можно представить в виде
следующей неявной зависимости инкремента ![]() от частоты модуляции и поля плоской волны
от частоты модуляции и поля плоской волны ![]() :
:
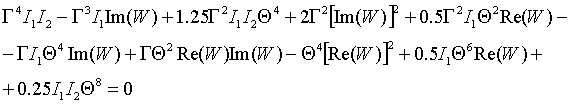 , (6)
, (6)
где ![]() - интенсивность
плоской волны,
- интенсивность
плоской волны, ![]() ,
, ![]() . Вещественные положительные корни этого
уравнения имеют место лишь в ограниченной области пространственных частот, где
имеется определённый экстремум, соответствующий наиболее неустойчивой модуляции
амплитудного профиля (см. рис. 1).
. Вещественные положительные корни этого
уравнения имеют место лишь в ограниченной области пространственных частот, где
имеется определённый экстремум, соответствующий наиболее неустойчивой модуляции
амплитудного профиля (см. рис. 1).
Рис. 1.
Коэффициент усиления ![]() , рассчитанный для амплитуды первой и
, рассчитанный для амплитуды первой и
второй
гармоник на расстояниях 1.5 ![]() , 2.0
, 2.0 ![]() , 2.5
, 2.5 ![]() , 3.0
, 3.0 ![]() , 3.5
, 3.5 ![]()
(сплошные линии), и функция видности ![]() оптической решетки
оптической решетки
на
длине ![]() (пунктирная
линия) в зависимости от пространственной
(пунктирная
линия) в зависимости от пространственной
частоты модуляции ![]() . Параметры пучков и
среды:
. Параметры пучков и
среды: ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Можно оценить также пороговое значение ![]() , при котором
возмущение на расстоянии
, при котором
возмущение на расстоянии ![]() становится сравнимым с амплитудой самой
волны:
становится сравнимым с амплитудой самой
волны:
К сожалению, описание развития неустойчивости (4-6), строго говоря, нельзя применять к пучкам и нестационарным волнам, так как ни неоднородность амплитуды волны, ни эффективная перекачка энергии между гармониками здесь не учитываются. Тем не менее, мы воспользуемся этими результатами, чтобы сравнить области генерации периодической структуры из двумерного эллиптического пучка с областью неустойчивости, рассчитанной по формулам (6-7), где в качестве амплитуды плоской волны используется пиковая амплитуда пучка (рис. 1).
4. Численное исследование формирования оптической решетки.
Для наблюдения распадной структуры сначала выбиралась нелинейная среда длиной 4ld. Проведенные численные эксперименты показывают, что при очень малых углах скрещивания решётка растёт очень слабо, тем более что говорить о решётке трудно, когда её период сравним с шириной входного пучка. Когда угол скрещивания способствует образованию периода возмущения, сравнимого с размерами стационарных пучков для заданной интенсивности, возмущение оказывается наиболее неустойчивым и пучок распадается на периодическую решётку (см. фильм 1).
1a.
2a.
3a.
4a.
b 
1b.
2b.
3b.
4b.
Фильм 1. Эволюция пучков первой (верхний фильм) и
второй (нижний фильм) гармоники на
длине ![]()
при
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При сравнительно частой модуляции профиля субпучки
испытывают сильную дифракцию, и распада не происходит. Эта картина
соответствует случаю плоских стационарных волн, рассмотренному выше, и является
общей для любой амплитуды пучка и фазовой расстройки среды. На рис. 2 показана
эволюция амплитудного профиля пучка на основной частоте при разных углах
падения слабого затравочного пучка. На рис. 2(а – г) видно, что
решётка с разным периодом «прорастает» с разной скоростью. Частота генерируемой
решётки совпадает с частотой модуляции пучка на входе, а её фазовый фронт определяет
фазовый фронт сильного пучка. Для количественной характеристики “качества” решётки
воспользуемся известной в оптике функцией видности
![]() :
:
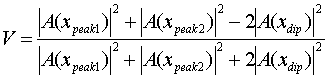 , (8)
, (8)
где первые два слагаемых в числителе и знаменателе представляют собой
интенсивность поля в двух соседних максимумах решётки, а третье слагаемое
описывает интенсивность поля в минимуме между этими пиками. При расчете
видности учитывается, что локализация максимумов на выходе среды должна
совпадать с их локализацией на входе. Кроме этого заметим, что из-за
неоднородности амплитудного профиля пучков расчет функции видности зависит от места
выбора амплитудных пиков. Так как решетка наиболее выражена в центре пучка, где
интенсивность поля максимальна, целесообразно рассчитывать видность в центре
генерируемой решетки. На рис. 1 пунктирной линией изображен график зависимости видности оптической решётки от пространственной частоты модуляции входного
пучка при амплитудах пучков ![]() ,
, ![]() и фазовой расстройке в среде
и фазовой расстройке в среде ![]() . График сопоставлен
на рисунке с теоретическим расчетом инкремента по формуле (6), если в качестве
амплитуды плоской волны взять пиковую амплитуду пучков. Интересно, что генерация
решетки происходит как раз в той области пространственных частот, неустойчивость
которой предсказывает теория плоских стационарных волн.
. График сопоставлен
на рисунке с теоретическим расчетом инкремента по формуле (6), если в качестве
амплитуды плоской волны взять пиковую амплитуду пучков. Интересно, что генерация
решетки происходит как раз в той области пространственных частот, неустойчивость
которой предсказывает теория плоских стационарных волн.
Если наблюдать за динамикой субпучков на расстояниях, когда их амплитуда становится сравнимой с полем исходной волны, можно заметить, что субпучки более не распространяются независимо. Из-за сильного параметрического взаимодействия между ними строгая периодичность оптической решётки быстро пропадает. Именно поэтому при большой мощности входного пучка, на выходе возникает сложная стохастическая картина, показанная на рис. 2 (д – з). В этих случаях нельзя корректно рассчитать функцию видности. Можно заметить, что правильная решетка развивается тогда, когда её частота близка к экстремуму зависимости инкремента модуляционной неустойчивости от частоты (рис. 2 е, ж). На малых пространственных частотах в области между усиливающимися субпучками решётки появляются дополнительные возмущения, которые нарушают заданную периодичность решётки (рис. 2 д). Они образуются из излучения формирующихся субпучков. Когда же частота модуляции достаточно высока, малые субпучки либо быстро дифрагируют, либо, если интенсивность поля высока, они распространяются так близко друг к другу, что сразу начинают эффективно взаимодействовать между собой - сливаться и расщепляться. Картина представляет собой повторяющуюся несинхронную взаимную перестройку пучков (рис.2 з). Многие исследователи полагают, что в результате модуляционной неустойчивости формируется серия близких солитонов. Активное неупорядоченное взаимодействие их с собственным излучением и друг с другом (слияние, расщепление и т.д.) получило название «солитонного газа».
б)  е)
е) 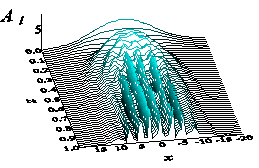
в)  ж)
ж) 
г) 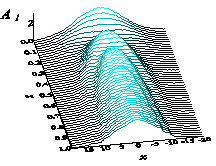 з)
з) 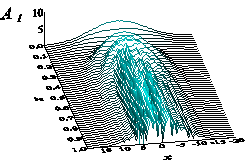
Рис. 2. Эволюция амплитудного профиля пучка основной частоты
в среде с параметрами ![]() при
скрещивании пучков
при
скрещивании пучков
с пиковыми амплитудами 3.0 и 0.1 (а - г) и 6.0 и 0.1 (д - з)
под углами ![]() , равными (а, д)
1.0, (б, е) 2.0, (в, ж) 3.0 и (г, з) 5.0.
, равными (а, д)
1.0, (б, е) 2.0, (в, ж) 3.0 и (г, з) 5.0.
5. Области генерации решетки и ее неустойчивость.
Как было выяснено, период затравочной модуляции, при
котором генерируется регулярная квазиодномерная решетка, ограничен по частоте
как сверху, так и снизу, причем расположение области пространственных частот
решетки неодинаково для разной амплитуды и фазовой расстройки в среде, так как
от этих параметров зависит диаметр солитона. Из анализа амплитудных профилей
пучка основной частоты на выходе из среды, была определена область частот
начальной модуляции и амплитуды мощного пучка, при которых происходит генерация
регулярной периодической решётки (рис. 3). При любой амплитуде входного
пучка в процессе увеличения частоты модуляции распределение выходной
интенсивности менялось от размытого изображения к контрастной картине
упорядоченных субпучков с заданной на входе пространственной частотой, и далее
снова к сглаженной или хаотической структуре. В качестве критерия образования
решётки мы опирались на следующее предположение: решетка тогда считалась возбужденной,
когда функция видности периодической структуры на выходе нелинейной среды превышает
½. Исходя из формулы (8), это эквивалентно отношению интенсивностей в
решетке ![]() .
Из теоретических предпосылок можно ожидать, что, так как с ростом интенсивности
усиливается взаимофокусировка пучков, область пространственных частот формируемой
решетки будет увеличиваться. Экспериментально найденная зависимость области
пространственных частот решетки от амплитуды пучка подтверждает наше предположение
(см. рис. 3). На этом же рисунке обозначена область развития модуляционной
неустойчивости, оцененная по формуле (7) для амплитуды пучков на расстоянии
.
Из теоретических предпосылок можно ожидать, что, так как с ростом интенсивности
усиливается взаимофокусировка пучков, область пространственных частот формируемой
решетки будет увеличиваться. Экспериментально найденная зависимость области
пространственных частот решетки от амплитуды пучка подтверждает наше предположение
(см. рис. 3). На этом же рисунке обозначена область развития модуляционной
неустойчивости, оцененная по формуле (7) для амплитуды пучков на расстоянии ![]() . Оказывается,
можно воспользоваться приближением плоских стационарных волн для определения
области генерации структуры, хотя, напомним, что такая теоретическая оценка
зависит от выбора амплитуды волн. Оцениваемая область немного сдвигается в сторону
высоких частот, если её рассчитывать по амплитуде пучков на более дальних
расстояниях, поэтому неудивительно, что высокочастотная решетка оказывается не
охваченной областью теоретического расчета (рис. 3).
. Оказывается,
можно воспользоваться приближением плоских стационарных волн для определения
области генерации структуры, хотя, напомним, что такая теоретическая оценка
зависит от выбора амплитуды волн. Оцениваемая область немного сдвигается в сторону
высоких частот, если её рассчитывать по амплитуде пучков на более дальних
расстояниях, поэтому неудивительно, что высокочастотная решетка оказывается не
охваченной областью теоретического расчета (рис. 3).
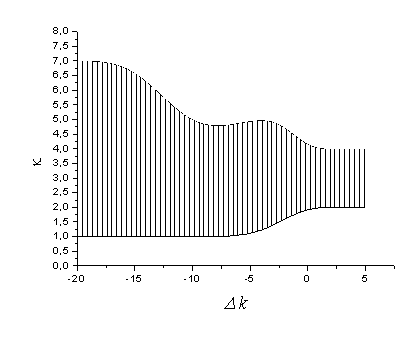
Рис. 3. Область значений пиковой амплитуды и частоты модуляции
мощного пучка, при которых на выходе квадратично-нелинейной
среды образуется периодическая решётка. Расстройка волновых
векторов ![]() . Длина среды
. Длина среды ![]() . Критерий V > ½.
. Критерий V > ½.
Эффективность взаимодействия
пучков гармоник сильно зависит от расстройки волновых векторов. В следующей
серии численных экспериментов мы наблюдали за образованием решетки при разных
значениях ![]() в
среде. Стоит заметить, что при каскадных перекачках энергии между гармониками в
зависимости от значения
в
среде. Стоит заметить, что при каскадных перекачках энергии между гармониками в
зависимости от значения ![]() скорость
нелинейного набега фаз у этих волн различна. В связи с этим среда может
оказывать фокусирующее или дефокусирующее действие на возбуждаемые пучки. В
частности, порог захвата пучка в солитон заметно понижается, если фазовая
расстройка
скорость
нелинейного набега фаз у этих волн различна. В связи с этим среда может
оказывать фокусирующее или дефокусирующее действие на возбуждаемые пучки. В
частности, порог захвата пучка в солитон заметно понижается, если фазовая
расстройка ![]() отрицательна [23].
При каскадной генерации решётки с этим знаком
отрицательна [23].
При каскадной генерации решётки с этим знаком
![]() ,
диапазон её частот самый широкий, в то время как при больших положительных
фазовых расстройках (
,
диапазон её частот самый широкий, в то время как при больших положительных
фазовых расстройках (![]() ) решетка
вообще не образуется. Оказывается, что при фазовом синхронизме сильное
взаимодействие между субпучками решетки и нелинейная аберрация пучка быстро
«портят» решетку, так что область формирования при
) решетка
вообще не образуется. Оказывается, что при фазовом синхронизме сильное
взаимодействие между субпучками решетки и нелинейная аберрация пучка быстро
«портят» решетку, так что область формирования при ![]() заметно сужается. Отметим, что
при
заметно сужается. Отметим, что
при ![]() угловой диапазон
возбуждения решётки уширяется почти в 3 раза по сравнению со случаем фазового
синхронизма
угловой диапазон
возбуждения решётки уширяется почти в 3 раза по сравнению со случаем фазового
синхронизма ![]() . Кроме того,
решётка при отрицательных
. Кроме того,
решётка при отрицательных
![]() оказывается
гораздо «чище» и более устойчива при своем распространении в среде. На
рис. 4 изображена найденная зона генерации решётки при разных
оказывается
гораздо «чище» и более устойчива при своем распространении в среде. На
рис. 4 изображена найденная зона генерации решётки при разных
![]() .
.
Рис. 4. Область значений фазовой расстройки волновых векторов и
частоты модуляции пучка, при которых на выходе образуется
периодическая решётка. Пиковые амплитуды пучков на
входе 4.0 и 0.1. Длина среды ![]() . Критерий V > ½.
. Критерий V > ½.
Как уже отмечалось, при распространении в
квадратично-нелинейной среде решётка может искажаться взаимодействием самих субпучков
решётки. При этом целесообразно говорить о длине, на которой решётка остаётся периодически
регулярной. В дальнейшей серии экспериментов пучки распространялись на более
дальние расстояния порядка
![]() . Эксперименты
показали, что независимо от параметров пучка и среды решётка неустойчива. На
определённом расстоянии происходит активное взаимодействие между соседними
пучками, и периодическая решётка исчезает. На рис. 5 показана эволюция
решётки при прохождении в квадратично-нелинейной среде расстояния
. Эксперименты
показали, что независимо от параметров пучка и среды решётка неустойчива. На
определённом расстоянии происходит активное взаимодействие между соседними
пучками, и периодическая решётка исчезает. На рис. 5 показана эволюция
решётки при прохождении в квадратично-нелинейной среде расстояния
![]() . Из сравнения двух снимков
распространения видно, что при отрицательной фазовой расстройке решетка
держится дольше, около
. Из сравнения двух снимков
распространения видно, что при отрицательной фазовой расстройке решетка
держится дольше, около
![]() , тогда
как при точном фазовом синхронизме пучки решетки отталкиваются и отдаляются друг
от друга на расстоянии уже чуть более
, тогда
как при точном фазовом синхронизме пучки решетки отталкиваются и отдаляются друг
от друга на расстоянии уже чуть более
![]() .
Это связано с наиболее эффективным взаимодействием субпучков при фазовом
синхронизме. При положительной фазовой расстройке решётка сохраняется хуже, чем
при отрицательной расстройке, но генерация все же более стабильна по сравнению
со случаем фазового синхронизма.
.
Это связано с наиболее эффективным взаимодействием субпучков при фазовом
синхронизме. При положительной фазовой расстройке решётка сохраняется хуже, чем
при отрицательной расстройке, но генерация все же более стабильна по сравнению
со случаем фазового синхронизма.
Рис. 5. Эволюция пучка основной частоты в квадратично-нелинейной
среде на больших расстояниях при пересечении пучков с пиковыми
амплитудами 4.0 и 0.1 на входе в
среду под углом ![]() .
.
Расстройка волновых векторов: (а) ![]() , (б)
, (б) ![]() .
.
Наконец, в численных экспериментах пучки задавались таким
образом, чтобы пересечение их центров происходило бы внутри нелинейной среды, а
не на входе. В отличие от линейной среды, где два когерентных пучка могут
интерферировать на любом расстоянии, в квадратично-нелинейной среде
промодулировать амплитудный профиль одного пучка другим наклонным пучком можно лишь
на расстояниях, малых по сравнению с длиной нелинейного взаимодействия
![]() . При пересечении на
больших расстояниях пучки не могут интерферировать как в линейной среде, так
как мощный пучок уже сильно связан со второй гармоникой, поэтому вместо
интерференции получается сложная картина взаимодействия пучков (рис. 6).
. При пересечении на
больших расстояниях пучки не могут интерферировать как в линейной среде, так
как мощный пучок уже сильно связан со второй гармоникой, поэтому вместо
интерференции получается сложная картина взаимодействия пучков (рис. 6).
Рис. 6. Эволюция пучков основной частоты в квадратично-нелинейной среде
при пересечении
пучков внутри среды на расстоянии ![]() . Расстояние между
. Расстояние между
центрами пучков ![]() . Пучки
пересекаются под углом
. Пучки
пересекаются под углом ![]() . На входе
. На входе
пучки имеют пиковые амплитуды
3.0 и 0.1. Фазовая расстройка среды ![]() .
.
6. Заключение.
В заключение отметим основные результаты, полученные в
работе. Предложенная группой Стегемана, Шика и Малендевича схема скрещенных
пучков основной частоты может быть использована для генерации в объемной
квадратично-нелинейной среде регулярной одномерной оптической решетки с
заданной пространственной частотой. Для генерации такой решетки необходимо
находиться в области параметров (периода возмущения, фазовой расстройки,
интенсивности пучка), рассчитанных в настоящей работе. Сравнение этой области с
областью положительного инкремента модуляционной неустойчивости, рассчитанного
в приближении плоских стационарных волн, показывает их хорошее соответствие. В
работе обнаружено, что квазиодномерная решетка неустойчива и при
распространении на расстояния более ![]() она
искажается взаимодействием соседних субпучков. Это характерное расстояние может
увеличиваться, если в среде существует большая отрицательная фазовая расстройка
и в то же время уменьшаться при увеличении интенсивности входного пучка. Выяснено
также, что невозможно добиться генерации решетки, если входные пучки пересекаются
внутри нелинейного кристалла на расстояниях порядка и более длины нелинейного
взаимодействия.
она
искажается взаимодействием соседних субпучков. Это характерное расстояние может
увеличиваться, если в среде существует большая отрицательная фазовая расстройка
и в то же время уменьшаться при увеличении интенсивности входного пучка. Выяснено
также, что невозможно добиться генерации решетки, если входные пучки пересекаются
внутри нелинейного кристалла на расстояниях порядка и более длины нелинейного
взаимодействия.
1. K. Tai, A. Hasegawa, and A. Tomita \\ Phys. Rev. Lett., V. 56, (1986) p. 135.
2. V. I. Bespalov, V. I. Talanov \\ J. Math. Phys. V.3 (1966) p. 307.
3. A.J.Campillo, S.L.Shapiro \\ Appl. Phys. Lett. V.23 (1973) p. 628.
4. A.Hasegawa, W.F.Brinkman \\ IEEE J. Quantum Electron. V.16 (1980) p. 694.
5. D.V.Skryabin, W.J.Firth \\ Phys. Rev. Lett V.60 (1999) p. 1019.
6. M.Soljacic, M.Segev \\ Phys. Rev. Lett V.84 (2000) p. 467.
7. J.P.Torres, C.Anastassiou \\ Phys. Rev. E V.65 (2001) p. 15601.
8. D.Kip, M.Soljacic \\ J. Opt. Soc. Am. B V.19 (2002) p. 502.
9. C.Cambournac, H.Maillotte \\ J. Opt. Soc. Am. B V.19 (2002) p.574.
10. L.Helczynski, D.Z.Anderson \\ IEEE J. Sel. Top. Quantum Electron. V.8 (2002) p.408.
11. G.Fibich, B.Ilan \\ Phys. Rev. Lett V.89 (2002) p. 13901.
12. A.V.Mamaev, M.Saffman \\ Phys. Rev. A V.54 (1996) p. 870.
13. J.Klinger, H.Martin \\ Opt. Lett. V.26 (2001) p.271.
14. R.A.Fuerst, D.M.Baboiu \\ Phys. Rev. Lett. V.78 (1997) p. 2756.
15. X.Liu, K.Beckwitt, F.W.Wise \\ Phys. Rev. Lett. V.85 (2000) p. 1871.
16. H.Fang, R.Malendevich \\ Opt. Lett. V.25 (2000) p. 1786.
17. D.M.Baboiu, G.I.Stegeman \\ Opt. Quantum Electron. V.30 (1998) p. 937.
18. S.Trillo, P.Ferro \\ Opt. Lett. V.20 (1995) p. 438.
19. J.F.Corney, O.Bang \\ Phys. Rev. Lett. V.87 (2001) p. 133901.
20. R.Schiek, H.Fang \\ Phys. Rev. Lett V.86 (2001) p. 4528.
21. A.K.Sukhorukova, A.P.Sukhorukov \\ Bull. RAS Physics V.63 (1999) p.1906.
22. А.К.Сухорукова, А.П.Сухоруков \\ Изв. РАН Сер. Физ. V.64 (2000) p.2344.
23. W.E.Torruellas, Z.Wang, D.J.Hagan, E.W.VanStryland, G.I.Stegeman, L.Torner, C.R.Menyuk \\ Phys. Rev. Lett V.64 (1995) p. 5036.

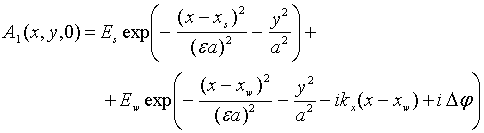

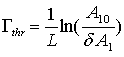 (7)
(7)
 д)
д)