УДК 621.396
КЛАССИФИКАТОР СИГНАЛОВ
Ю.Н.Кликушин*, К.Т. Кошеков**,
*Омский государственный технический университет, Россия
**Северо-Казахстанский государственный университет им. М. Козыбаева, Республика Казахстан
Получена 13 октября 2007 г.
Описан алгоритм работы и библиотека инструментов виртуального классификатора сигналов, представленных своими выборочными реализациями. В качестве собственных имен классов используются имена симметричных распределений случайных величин. Классификатор позволяет строить деревья, упорядоченные по вертикали (общности свойств, сверху вниз) и по горизонтали (похожести сигналов, слева направо). Представлен пример применения данного виртуального прибора для иерархической классификации группы сложных сигналов по их временным, вероятностным, спектральным и корреляционным характеристикам.
ФУНКЦИОНАЛЬНОЕ НАЗНАЧЕНИЕ И ОБЛАСТЬ ПРИМЕНЕНИЯ
Функциональное назначение – классификация сложных периодических и случайных сигналов, а также их смесей.
Область применения библиотеки классификатора – интеллектуальные системы измерения, управления, контроля и диагностики.
ИСПОЛЬЗУЕМЫЕ ТЕХНИЧЕСКИЕ СРЕДСТВА
Включают персональный компьютер типа PENTIUM-3 и выше с 64 МБ (и выше) оперативной памяти.
СПЕЦИАЛЬНЫЕ УСЛОВИЯ ПРИМЕНЕНИЯ
Определяются конкретной предметной областью применения и оговариваются в техническом задании.
УСЛОВИЯ ПЕРЕДАЧИ ДОКУМЕНТАЦИИ
Техническая документация передается заказчику на договорной основе с заявителем.
ТЕХНИЧЕСКОЕ ОПИСАНИЕ
Интеллектуальная мощь систем обработки данных во многом зависит от их способности проводить автоматическую классификацию анализируемых сигналов. Под классификацией понимается разделение группы объектов на некоторые части – подгруппы, внутри которых объекты имеют общие (в определенном смысле) свойства. Опцию классификации можно реализовать, используя методы, принятые в прикладной статистике и теории распознавания образов [1-3]. Однако, из-за математической и алгоритмической сложности, эти методы практически не применяются в системах реального времени.
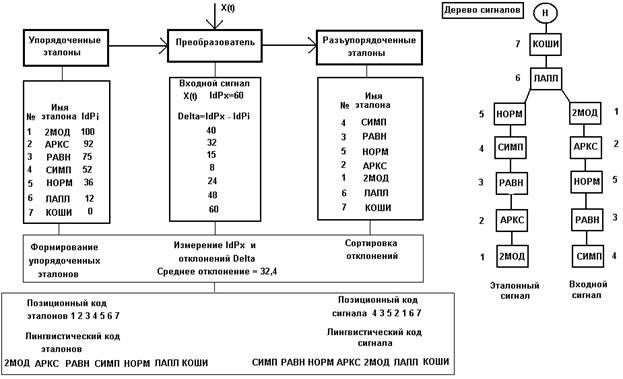
Предлагаемые виртуальные инструменты используют новую методологию классификации сигналов вообще и их распознавания, в частности. Эта методология основана на идеях и моделях идентификационных измерений (ИИ) сигналов, изложенных в монографиях [4,5]. Суть предложения иллюстрирована рис. 1 и сводится к тому, что первоначально (в отсутствие сигнала) упорядоченная, например, по убыванию, система объектов-эталонов, под воздействием входного сигнала - разъупорядочивается (эталоны меняют свои позиции). Новый порядок следования объектов-эталонов отображает классификационную структуру анализируемого сигнала. Номера позиций образуют позиционный код (ПК), а, соответствующие им, имена объектов-эталонов – лингвистический код (ЛК) входного сигнала. Два и более сигналов находятся в одном классе, если они имеют одинаковые позиционные или лингвистические коды. Более того, согласно гипотезе компактности [3], принятой в теории распознавания образов, если сигналы находятся в одном классе, то можно утверждать (с определенной долей вероятности), что они в чем-то похожи. Таким образом, с позиции теории ИИ, классификация сигналов есть относительное измерение их неупорядоченности или хаоса. В этом отношении ИИ сродни фрактальным измерениям [6].
Рис.1. Структурная схема классификатора сигналов
Рис.2. Структурная схема программного кода классификатора сигналов
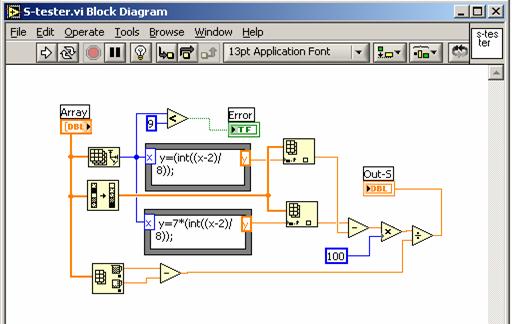
На рис. 2 представлена структурная схема программного кода классификатора, выполненная в среде LabVIEW-7.1. В данной схеме использованы как стандартные библиотечные элементы (Subtract, Absolute Value, Build Array, Sort 1D Array, Divide, Add Array Elements, Delete from Array), так и модули (S-tester, Name_Former), разработанные авторами специально.
Исследуемая выборка сигнала измеряется идентификационным тестером S-типа [7], на выходе которого формируется число (IdPx=60 для примера на рис.1). Это число сравнивается с упорядоченным набором подобных идентификационных чисел, принадлежащих эталонам, в качестве которых используются имена случайных сигналов с двумодальным (2МОД), арксинусным (АРКС), равномерным (РАВН), треугольным (СИМП), нормальным (НОРМ), двусторонним экспоненциальным (ЛАПЛ) и Коши (КОШИ) распределениями. Для указанных эталонов значения идентификационных чисел (IdPi) известны заранее и хранятся внутри программы как некие константы. Диапазон идентификационных чисел эталонов (от 0 до 100) охватывает полный диапазон существования любых других сигналов, как случайных, так и периодических.
Сравнение идентификационных чисел входного сигнала и эталонов осуществляется путем вычисления абсолютной разности (Delta) с формированием соответствующего массива. Обработка массива отклонений заключается в его сортировке совместно с именами эталонных распределений так, что на выходе системы формируется позиционный и лингвистический коды (ПК, ЛК). Позиционный и лингвистический коды перечисляют, соответственно, номера и имена эталонов сортированного массива. На рис. 1 показано как из линейно упорядоченного ПК = 1234567 эталонов получился разъупорядоченный ПК = 4352167 входного сигнала. Потенциально общее число возможных ПК сигналов определяется числом перестановок и для 7 эталонов составляет величину, равную 7!=5240. В реальных системах, как правило, требуемое число различимых градаций составляет величину в 3-5 раз меньшую. Поэтому данный классификатор можно без особой доработки включать в качестве интеллектуального модуля в состав многих практических систем обработки и анализа данных.
Классификационное дерево (правая часть рис.1) сигналов строится из предположения о том, что разряды ПК являются потенциальными узлами ветвления. При этом исходная ветвь эталонов является крайней левой. Ветви всех остальных сигналов располагаются правее, на расстоянии пропорциональном среднему отклонению. Таким образом, происходит упорядочивание ветвей дерева по горизонтальному направлению (слева - направо). Вертикальная упорядоченность (сверху - вниз) соответствует изменению степени общности сигналов по принципу "от общего к частному". В рассматриваемом примере (рис.1) у эталонного и анализируемого сигналов общими являются два разряда с именами КОШИ и ЛАПЛ из семи. Это дает возможность количественно оценить степень общности как:
т.е. 2/7=0,2857.
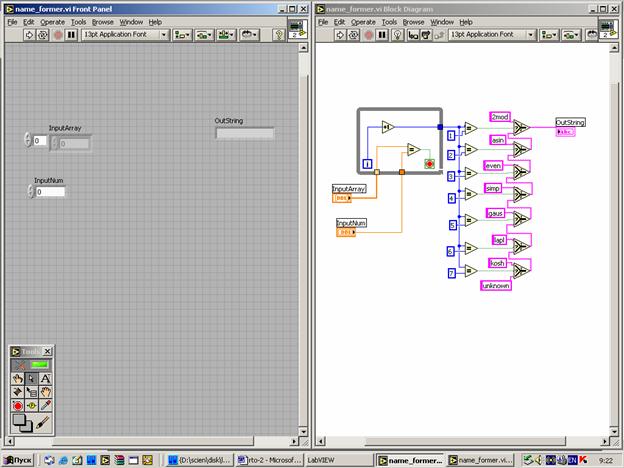
Принцип действия S-тестера, входящего в состав библиотеки классификатора, основан на измерении крутизны среднего участка ранжированной функции сигнала. Его программная реализация представлена на рис. 3. Модуль Name_former (рис.4) предназначен для обработки списка эталонов по значениям отклонения Delta. На выходе этого модуля формируется имя эталона, соответствующее заданному на входе InputNum значению отклонения.
Рассмотрим технологию применения классификатора для решения следующей задачи. Имеется группа из 4-х сигналов с именами: 4-4-1n.wav, 4-4-2n.wav, 4_4idle.wav, 4_4tfc.wav.
Рис.3. Структура программного кода S-тестера
Рис.4. Панель управления и программный код модуля Nsme_former
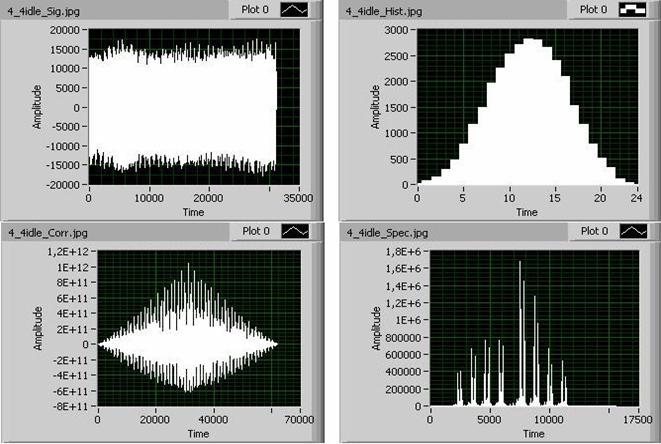
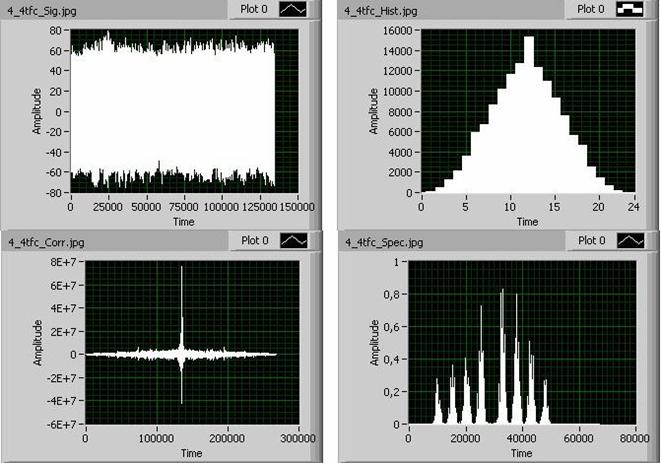
Необходимо выяснить взаимосвязь между этими сигналами. Решение сводится, во-первых, к выполнению операции измерения идентификационных параметров основных характеристик сигналов, к которым относятся временная (Time), вероятностная (Hist), спектральная (Spec) и корреляционная (Corr). Соответствующие результаты измерения сведены в табл. 1, где представлены также результаты измерения идентификационных параметров эталонов (2mod, asin, even, simp, gaus, lapl, kosh).
Таблица 1
№
Имя файла
Time
Hist
Corr
Spec
1
4-4-1n.wav
47,252747
93,2344
0,705318
0,0149
2
4-4-2n.wav
43,434343
94,6411
1,799429
0,0652
3
4_4idle.wav
38,773553
92,2885
4,540104
0,0194
4
4_4tfc.wav
36,363636
75,5248
0,362961
2,0658
5
2mod.txt
100
0
1,474858
23,29
6
asin.txt
92,2945
26,2704
1,465952
21,999
7
even.txt
75,420626
52,5
1,466273
17,493
8
simp.txt
49,942408
78,8036
1,491746
25,888
9
gaus.txt
30,710666
84,1256
1,44303
16,594
10
lapl.txt
11,775648
24,8674
1,458223
22,51
11
kosh.txt
0,055596
0,03011
0,09208
39,541
Таблица 2
№
Имя файла
Имя эталона
Time
PC
Hist
PC
Corr
PC
Spec
PC
1
4-4-1n.wav
2mod.txt
52,75
4
93,23
5
0,7695
7
23,27
5
2
4-4-1n.wav
asin.txt
45,04
5
66,96
4
0,7606
5
21,98
3
3
4-4-1n.wav
even.txt
28,17
3
40,73
3
0,761
6
17,48
2
4
4-4-1n.wav
simp.txt
2,69
6
14,43
2
0,7864
2
25,87
6
5
4-4-1n.wav
gaus.txt
16,54
2
9,109
6
0,7377
3
16,58
1
6
4-4-1n.wav
lapl.txt
35,48
7
68,37
7
0,7529
1
22,49
4
7
4-4-1n.wav
kosh.txt
47,2
1
93,2
1
0,6132
4
39,53
7
Delta
28,08203046
32,55
55,15
0,7402
23,89
8
4-4-2n.wav
2mod.txt
56,57
4
94,64
5
0,3246
4
23,22
5
9
4-4-2n.wav
asin.txt
48,86
5
68,37
4
0,3335
1
21,93
3
10
4-4-2n.wav
even.txt
31,99
6
42,14
3
0,3332
3
17,43
2
11
4-4-2n.wav
simp.txt
6,508
3
15,84
2
0,3077
2
25,82
6
12
4-4-2n.wav
gaus.txt
12,72
7
10,52
6
0,3564
6
16,53
1
13
4-4-2n.wav
lapl.txt
31,66
2
69,77
7
0,3412
5
22,44
4
14
4-4-2n.wav
kosh.txt
43,38
1
94,61
1
1,7073
7
39,48
7
Delta
28,50474814
33,1
56,56
0,5291
23,84
15
4_4idle.wav
2mod.txt
61,23
5
92,29
5
3,0652
4
23,27
5
16
4_4idle.wav
asin.txt
53,52
4
66,02
4
3,0742
1
21,98
3
17
4_4idle.wav
even.txt
36,65
6
39,79
3
3,0738
3
17,47
2
18
4_4idle.wav
simp.txt
11,17
3
13,48
2
3,0484
2
25,87
6
19
4_4idle.wav
gaus.txt
8,063
7
8,163
6
3,0971
6
16,57
1
20
4_4idle.wav
lapl.txt
27
2
67,42
7
3,0819
5
22,49
4
21
4_4idle.wav
kosh.txt
38,72
1
92,26
1
4,448
7
39,52
7
Delta
28,77967418
33,76
54,2
3,2698
23,88
22
4_4tfc.wav
2mod.txt
63,64
5
75,52
4
1,1119
7
21,22
5
23
4_4tfc.wav
asin.txt
55,93
4
49,25
5
1,103
5
19,93
3
24
4_4tfc.wav
even.txt
39,06
6
23,02
3
1,1033
6
15,43
2
25
4_4tfc.wav
simp.txt
13,58
7
3,279
2
1,1288
2
23,82
6
26
4_4tfc.wav
gaus.txt
5,653
3
8,601
6
1,0801
3
14,53
1
27
4_4tfc.wav
lapl.txt
24,59
2
50,66
7
1,0953
1
20,44
4
28
4_4tfc.wav
kosh.txt
36,31
1
75,49
1
0,2709
4
37,47
7
Delta
24,44050754
34,11
40,83
0,9847
21,84
Вторым шагом является вычисление отклонений каждого сигнала с эталонами по всем характеристикам и определение позиционных кодов (РС). Соответствующие результаты представлены в табл. 2. Так, например, отклонение сигнала 4-4-1n.wav от группы эталонов по временной характеристике составляет 32,55, а по всем характеристикам - 28,082.
Третий шаг состоит в анализе позиционных кодов и в построении по ним классификационных деревьев. Согласно данным табл.2, все сигналы имеют один и тот же ПК (5326147) по спектральной характеристике (Spec). Это означает, что анализируемые сигналы имеют похожие спектры. Дерево будет содержать одну ветвь, на которой "развешано" 4 сигнала в порядке возрастания отклонений (табл. 3).
Таблица 3
PC Spectrum
5326147
Порядок
1
2
3
4
Отклонение
21,84
23,84
23,88
23,89
Имя файла
4_4tfc.wav
4-4-2n.wav
4_4idle.wav
4-4-1n.wav
Второй по общности является вероятностная характеристика (Hist), которая имеет 2 разновидности позиционного кода, причем один из кодов объединяет 3 сигнала (табл. 4).
Таблица 4
PC Histogram
4532671
5432671
Порядок
1
1
2
3
Отклонение
40,83
54,2
55,15
56,56
Имя файла
4_4tfc.wav
4_4idle.wav
4-4-1n.wav
4-4-2n.wav
Позиционный код корреляционной характеристики (Corr) также имеет две разновидности, в каждой из которых содержатся по два сигнала (табл. 5).
Таблица 5
PC Correlation
4132657
7562314
Порядок
1
2
1
2
Отклонение
0,5291
3,2698
0,7402
0,9847
Имя файла
4-4-2n.wav
4_4idle.wav
4-4-1n.wav
4_4tfc.wav
Позиционный код временной характеристики (Time) содержит 4 разновидности позиционного кода (табл. 6) и потому отображает скорее не общие, а частные свойства сигналов.
Таблица 6
PC Time
4536271
4563721
5463721
5467321
Порядок
1
1
1
1
Отклонение
32,55
33,1
33,76
34,11
Имя файла
4-4-1n.wav
4-4-2n.wav
4_4idle.wav
4_4tfc.wav
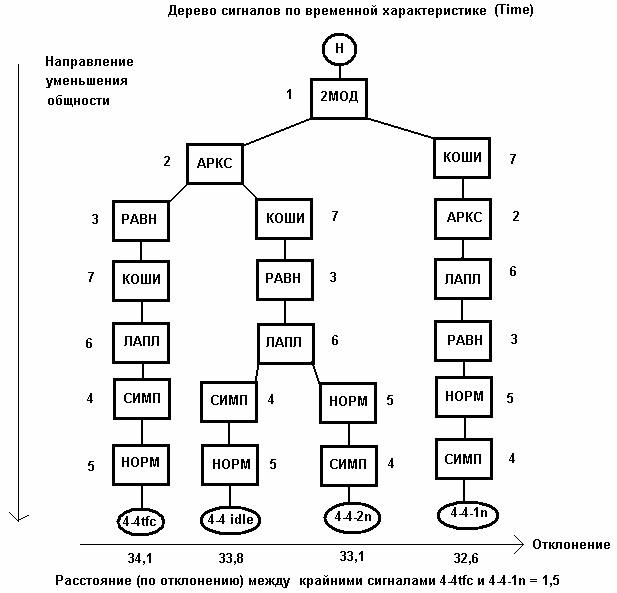
Дерево сигналов для временной характеристики изображено на рис. 5. Построение дерева начинается с младшего правого разряда ПК, поскольку значение этого разряда (1=2МОД) является общим для всех сигналов. После первого разряда образуется ветвление по 2 направлениям: к значению 7 (один сигнал с именем 4-4-1n.wav) и к значению 2 (три сигнала с именами 4-4-2n.wav, 4_4idle.wav4, _4tfc.wav). Следующее ветвление образуется на третьем разряде по направлениям 3 (4_4tfc.wav) и 7 (4-4-2n.wav, 4_4idle.wav). Последнее ветвление на 6 разряде разделяет два сигнала 4-4-2n.wav и 4_4idle.wav.
В отличие от известных методов построения классификационных деревьев предлагаемый виртуальный инструмент реализует такой метод, при котором структура группы сигналов не только визуализируется, но и упорядочивается как по вертикали (по общности), так и по горизонтали (по отклонению).
Рис. 5. Дерево сигналов для временной характеристики
Визуальные образы характеристик анализируемых сигналов представлены на рис. 6-9, используя которые можно удостовериться в правильности работы классификатора, а также сформировать новые подходы к интерпретации понятия "похожести" сигналов. В частности, сигнал 4-4-2n.wav по отклонению (Delta=0,5) расположен ближе всего к сигналу 4-4-1n.wav. Однако по степени общности (0,71) этот же сигнал ближе всего к сигналу 4_4idle.wav. Отсюда возникает предложение - оценивать "похожесть" сигналов некоторым комплексным показателем, учитывающим как значение отклонения, так и степень общности, например, в логической форме:
где Cij – степень общности (вложенности), оцениваемая по формуле (1), Δij – значение отклонения меду сигналами, Δmax – максимальное отклонение между крайними сигналами данного дерева. Если применить формулу (2) к оценке похожести сигнала 4-4-2n.wav к сигналам 4-4-1n.wav и 4_4idle.wav, то получим результат (табл. 7) сравнения в пользу сигнала 4_4idle.wav.
Таблица 7
Оцениваемый сигнал
4-4-2n.wav
Степень общности, Сij
Относительное отклонение Δij / Δmax
Степень похожести, Пij
1-ый сравниваемый сигнал 4-4-1n.wav
0,14
0,33
0,67
2-ой сравниваемый сигнал 4_4idle.wav
0,7
0,47
0,7
Таким образом, расчет по формуле (2) показывает, что наиболее похожим к сигналу 4-4-2n.wav является сигнал 4_4idle.wav.
Рис. 6. Графики временной, вероятностной, корреляционной и спектральной характеристик (слева направо, сверху вниз) сигнала 4-4-1n.wav
Рис. 7. Графики временной, вероятностной, корреляционной и спектральной характеристик (слева направо, сверху вниз) сигнала 4-4-2n.wav
Рис. 8. Графики временной, вероятностной, корреляционной и спектральной характеристик (слева направо, сверху вниз) сигнала 4-4idle.wav
Рис. 9. Графики временной, вероятностной, корреляционной и спектральной характеристик (слева направо, сверху вниз) сигнала 4-4tfc.wav
ЛИТЕРАТУРА
1. Прикладная статистика: Классификация и снижение размерности: Справ. Изд./ Под ред. С.А. Айвазяна. – М.: Финансы и статистика, 1989. – 607 с.
2. Васильев В.И. Распознающие системы. – Киев: Наукова Думка, 1969. – 292 с.
3. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. – Новосибирск: Изд-во Ин-та математики им. С.Л. Соболева СО РАН, 1999. – 270 с.
4. Кликушин Ю.Н. Технологии идентификационных шкал в задаче распознавания сигналов // Монография. - Омск: Изд-во ОмГТУ, 2006 - 96 с.
5. Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов: Монография. – Петропавловск, СКГУ им. М.Козыбаева, 2007. – 186 с.
6. Федер Е. Фракталы. - М.: Мир, 1991.
7. Кликушин Ю.Н. Библиотека виртуальных инструментов анализа и синтеза формы сигналов // Свидетельство о госрегистрации №50200601945, Министерство образования и науки РФ, ОФАП. - М.: 2006.
8. Измерения в электронике // Справочник. Под ред. В.А.Кузнецова. – М.: Энергоатомиздат, 1987. – 511 с.
9. Кликушин Ю.Н. Библиотека виртуальных инструментов анализа и синтеза формы сигналов. - Свидетельство об отраслевой регистрации, №50200601945, Министерство образования и науки РФ, ОФАП, М.: 2006.
10. Кликушин Ю.Н. Классификационные шкалы для распределений вероятности. - Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2000 г.
11. Кликушин Ю.Н., Кошеков К.Т. Исследование эволюции бинарных смесей сигналов. - Вестник КазНУ.- Казахский Национальный Университет им. Аль-Фараби, Серия математика, механика, информатика. – Алматы: №1(44), с.94-100, 2005.
| xxx |

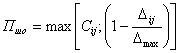 , (2)
, (2)