“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 10, 2009

оглавление

Определение области принятия решений бортового радиолокационного датчика цели

А. Б. Борзов, К. П. Лихоеденко, И. В. Муратов, Г. Л. Павлов, В. Б. Сучков

МГТУ им. Н.Э.Баумана

Получена 11 августа 2009 г.

Рассмотрены математическая модель и алгоритм вычисления импульсного сигнала, отраженного от цели, заданной своей многоточечной моделью. Рассмотрена возможность использования метода математического моделирования областей принятия решений (ОПР) импульсных бортовых радиолокационных датчиков цели (БРДЦ) на основе многоточечной модели радиолокационной цели. Приведены результаты расчета одиночных импульсов и последовательности импульсов, отраженных от различных радиолокационных целей на траектории относительного движения ракеты и цели, а также соответствующие им ОПР БРДЦ.

Ключевые слова: радиолокация, многоточечная модель радиолокационной цели, бортовые радиолокационные датчики цели.

В задачах по оценке эффективности средств доставки математическая модель входных сигналов БРДЦ используется на этапе определения области принятия решений (ОПР) БРДЦ при известном алгоритме функционирования исполнительного устройства. В настоящее время разработан ряд математических моделей и программных комплексов [1-2], предназначенных для расчета входных сигналов БРДЦ на траектории относительного движения цели, предназначенных как для использования в комплексах полунатурного моделирования, так и при непосредственном проведении расчетов по проектированию БРДЦ.

Одна из методик расчета входных сигналов БРДЦ [1] основана на представлении геометрической модели цели в виде полигональной модели, которая аппроксимирует поверхность цели в виде совокупности плоских треугольных элементов (полигонов). Данная методика расчета характеризуется максимальной степенью достоверности по сравнению с данными экспериментов, поскольку позволяет наиболее точно формализовать геометрию поверхности цели и соответственно учесть электродинамические эффекты, имеющие место в условиях ближней зоны локации. Поскольку в модели сигнала БРДЦ учитываются сложные волновые процессы, такие как дифракция волн на острых кромках, переотражения волн между элементами конструкции цели, нестационарный характер ее облучения и др., то необходимая точность достигается при количестве полигонов не менее , что в свою очередь приводит к большим временным затратам на вычисление. Поэтому при проведении практических расчетов по проектированию БРДЦ в настоящее время используют «быстрые» многоточечные модели [2]. Использование многоточечных моделей, образованных из 10-20 точек дает возможность избежать математического описания геометрии цели и соответственно значительно сократить время расчета при неизбежном снижении точности вычислений.

В настоящее время в МГТУ им. Н.Э.Баумана разработана многоточечная модель (ММ) цели, которая основана на преобразовании полигональной модели цели в совокупность небольшого сила точек с заранее просчитанными диаграммами ЭПР в ближней зоне локации. Основные принципы формирования этой модели приведены в [2]. При расчете входных сигналов БРДЦ по данной модели считается, что БРДЦ работает в непрерывном режиме излучения. Поэтому для проектирования и тестирования импульсных БРДЦ требуется соответствующая модификация ММ [2]. Целью данной статьи является создание математической модели расчета входных сигналов БРДЦ, работающего в импульсном режиме излучения, на основе многоточечной модели цели.

 

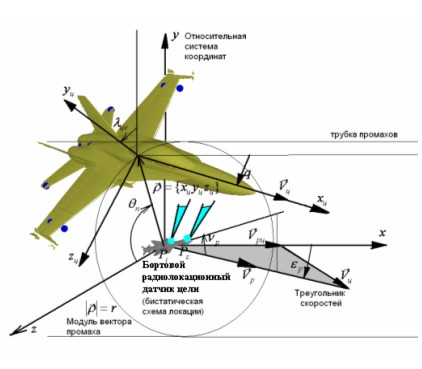
Рис. 1. Относительная система координат БРДЦ и цели.

 

Для расчета входных сигналов БРДЦ траектория относительного движения цели задается в относительной системе координат (ОСК)  (рис.1), начало которой, точка , совмещается с центром системы координат средства доставки (ракеты) . Орт  ОСК направлен по вектору относительной скорости и лежит в плоскости, образованной векторами скоростей  ракеты и цели, а также вектором  относительной скорости . Эти вектора образуют треугольник скоростей. Орт  перпендикулярен плоскости треугольника скоростей, а орт  дополняет ОСК до правой. В качестве параметров, определяющих условия встречи, принимаются курсовой угол ракеты e_р  - угол между  и , курсовой угол цели q - угол между вектором скорости цели  и , угол крена цели l_цv - угол между плоскостью планера ракеты и плоскостью треугольника скоростей,  - угол атаки ракеты.

Координата принятия решений (КПР) БРДЦ  в ОСК соответствует продольной координате  условной точки цели и вектором ее промаха , где  - величина промаха, а  - угол по трубке промахов, отсчитываемый от оси  по часовой стрелке (рис.1). Совокупность КПР во всей области изменений параметров условий встречи БРДЦ и цели определяет ОПР БРДЦ.

Методом математического моделирования пространственная конфигурация границ ОПР определяется в виде совокупности М плоских кривых, представленных в виде дискретной совокупности точек принятия решения БРДЦ по цели в плоскости угла по трубке промахов  для N значений координат  и промахов  в ОСК:

                                                                                     (1)

Границы ОПР для каждого значения промаха определяются как , , где ,  – математическое ожидание и среднеквадратичное отклонение координаты принятия решения БРДЦ.

При расчете мощности входного сигнала БРДЦ на траектории движения цели, заданной своей многоточечной моделью, используются массивы значений ЭПР и начальной фазы локальных отражателей, рассчитанные на этапе формирования многоточечной модели. В соответствии с представлением цели в виде набора локальных отражателей напряжение возникающее в нагрузке приемной антенны БРДЦ от воздействия m-й точки многоточечной модели в ближней зоне локации, определяется следующим образом [2]:

,                                                     (2)

,                                                                                                   (3)

где  - комплексный коэффициент отражения точки, ,  - ЭПР и начальная фаза m-й точки, которая вычисляется за счет интерполяционных соотношений для соседних значений диаграммы ЭПР и фазы.

Рассмотрим формирование отраженного от цели сигнала при импульсном воздействии передатчика. Единичный импульс колебаний, генерируемых передатчиком БРДЦ, представляется в виде:

,                                                                                   (4)

где  - амплитуда зондирующего импульса, постоянная в каждом периоде повторения,  - частота несущего колебания,  - длительность импульса, T – период повторения импульсов,  - начальная фаза колебания, t – время, отсчитываемое от начала периода повторения.

Последовательность N импульсов, излучаемых передатчиком, определяется по аналогии с (4) в следующем виде:

 

,                                                                     (5)

где n=0,1..N-1 – номера излучаемых импульсов.

Для общности рассуждений будем рассматривать отраженный сигнал только для одного импульса (5), принимая во внимание, что импульсная последовательность может быть представлена как совокупность одиночных импульсов (4).

Величина напряжения одиночного импульса, отраженного от m-й точки, принятого на входе приемника имеет вид:

,                                         (6)

где амплитуда отраженного импульса  определяется из (2), начальная фаза отраженного импульса определяется как аргумент комплексной функции ,  - временная задержка импульса с учетом его распространения от передатчика до точки цели и от точки к приемнику (рис. 2).

Рис. 2 Схема формирования временной задержки и доплеровской частоты от m-й точки многоточечной модели цели.

 

 

Значение частоты Доплера, возникающее от эффекта взаимного перемещения передатчика, приемника и точки цели определяется в общем случае разнесения передатчика и приемника в следующем виде:

,                                                                               (7)

где  - относительная скорость ракеты и цели,  - направляющий вектор из точки модели цели в фазовый центр антенны передатчика (приемника) (рис. 2).

Для преобразования отраженного радиосигнала в комплексную огибающую на видеочастоте сигнал  (6) подается на два фазовых детектора, опорные напряжения которых  и  сдвинуты по фазе на  друг относительно друга, а в остальном с точностью до амплитуды являются копиями излучаемого сигнала. В простейшей конструкции фазовых детекторов процесс преобразования включает умножение входных сигналов и низкочастотную фильтрацию результирующего сигнала. При этом на выходе фильтров нижних частот в полосе ожидаемых доплеровских частот формируются следующие сигналы от m-й точки:

.                                                     (8)

Сигналы (8) можно рассматривать как действительную и мнимую составляющие комплексной огибающей отраженного сигнала.

.

где  - время, отсчитываемое от начала импульса.

Результирующие составляющие сигналов, принятых от всей цели, определяются в результате суммирования отдельных импульсов (7) принятых в разные интервалы времени  по всем точкам цели:

,                                             (9)

           

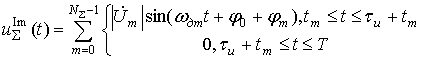
 - количество точек многоточечной модели.

Для обеспечения селекции цели по дальности видеоимпульс (9) с выхода УПЧ умножается на стробирующий импульс, длительность которого определяется требуемым интервалом дальностей:

,                            (10)

,                                                                                    (11)

где , .

Тогда модуль комплексной огибающей единичного импульса, отраженного от всей цели с учетом локальных задержек импульсов от отдельных отражателей, имеет следующий вид в единицах мощности:

,                    (12)

где  - сопротивление излучения антенны.

В связи с тем, что реализовать расчет огибающей мощности отраженного сигнала по формулам (8-12) в аналоговой форме не представляется возможным, будем представляет зондирующий и отраженный импульсы в виде набора дискретных отсчетов, для которых значения времени определяются из соотношения:

,                                                                                                 (13)

где  - номер отсчета в пределах каждого одиночного импульса,  - номер периода повторения,  - количество отсчетов в пределах импульса,  - количество импульсов повторения на траектории движения цели.

В соответствии с (13) величины напряжения квадратурных сигналов и огибающей мощности входного сигнала представляют собой двумерные массивы данных:

, , .                                                     (14)

В каждой из двумерных матриц (14) в столбцах хранятся значения квадратурных напряжений и мощности для каждого одиночного импульса, а номер столбца определяет номер периода повторения l.

В классической теории сигналов количество отсчетов в пределах импульса  определяется на основе теоремы Котельникова . В связи с тем, что суммирование сигналов по формуле (10) осуществляется на видеочастотах необходимо задаваться другими критериями. В соответствии с (10) для максимально корректного суммирования импульсов от каждого из отражателей с учетом локальной задержки и фазы необходимо, чтобы интервал дискретизации временной шкалы наблюдения не превышал минимально возможной задержки импульса от каждого из отражателей:

,                                                                                                                    (15)

где  - минимальное расстояние между двумя соседними токами многоточечной модели.

При выборе  при проведении практических расчетов будем прежде всего исходить из минимизации временных затрат на вычисления при соблюдении минимальной точности суммирования. Таким образом, в расчетах будем принимать величину интервала дискретизации из расчета пяти отсчетов на один импульс: . Тогда количество дискретных отсчетов сигнала на один импульс определяется отношением периода повторения к величине интервала дискретизации:

.

Количество импульсов  в (15) определяется исходя из параметров траектории движения цели, периодом повторения и относительной скорости. Траектория относительного движения цели в ОСК представляет собой прямую линию, соединяющую начальное  и конечное  положение условной точки цели при ее движении параллельно оси x ОСК (рис. 1). Предполагается, что при движении цели по относительной траектории изменяется только координата x ее условной точки, а координаты y и z остаются неизменными. Определение координат {y_ц,z_ц} осуществляется для заданных значений промаха r и угла по трубке промахов  из следующих соотношений ,  (рис. 1). Координаты начального x_ц0 и конечного x_цk положений цели в ОСК при движении цели по траектории, задаются в качестве исходных параметров. Траектория относительного движения цели в ОСК формируется из совокупности дискретных кадров , m=0,1..N_x. Число импульсов  определяется числом ракурсов наблюдения, которое определяется из соотношения:. Шаг по траектории движения  определяется произведением относительной скорости движения ракеты и цели на период повторения: . Таким образом, необходимо изменять положение цели на траектории движения только после приема очередного отраженного импульса.

Выбор периода повторения импульсов должен выбираться из возможностей БРДЦ осуществлять доплеровскую селекцию целей в диапазоне ожидаемых относительных скоростей . Очевидно, что в диапазоне относительных скоростей максимальная ожидаемая частота Доплера определяется в виде . Будем  считать, что период повторения должен быть таким, чтобы в его пределах укладывалось как минимум 10 периодов повторения доплеровского сигнала, т.е. T ≥ 10/f_{d max}.

Для каждого кадра программа должна преобразовать координаты фазового центра антенн БРДЦ, а также векторов базиса антенны в систему координат цели (СКЦ) для дальнейшего вычисления мощности. Преобразование координат осуществляется на основе матриц преобразования из ОСК в систему координат ракеты (СКР) и СКЦ соответственно. Для заданных условий встречи координаты базисных ортов СКР и СКЦ определяются из следующих соотношений:

, , ,

,,

.

Тогда матрицы преобразований координат из ОСК в СКР и СКЦ получим в следующем виде:

, .

С учетом соотношений для преобразований координат и матриц преобразования координаты фазового центра антенны в СКЦ определяются из следующих соотношений:

,

,

.

 

В качестве вектора оси антенны  будем рассматривать единичный вектор, который ориентирован из фазового центра антенны перпендикулярно оси ракеты вдоль оси y ОСК. Исходя из конструктивных особенностей антенны, закрепленной на ракете, будем считать, что базовый вектор поляризационного базиса антенны  ориентирован в направлении оси ракеты и в ОСК имеет следующие координаты . В соответствии с преобразованиями координат и матриц преобразования получим координаты вектора поляризационного базиса антенны в СКЦ:

,

,

.

Второй вектор поляризационного базиса антенны в СКЦ определяется в результате векторного произведения . При проведении полунатурных испытаний поляризация антенны задается линейной и согласованной для передающей и приемной антенн.

После преобразований координат фазового центра антенны и векторов базиса антенны для каждого кадра массива траекторий относительного движения формируется единый файл траектории, который используется при вычислении мощности отраженного сигнала (12,14).

На основе описанной методики были проведены расчеты последовательности импульсов отраженных от различных целей (ракета "Гарпун", морская поверхность), заданных своими многоточечными моделями. Параметры БРДЦ, для которого вычислен отраженный сигнал от цели, были заданы следующими: мощность излучения P_i=1 Вт, КНД передающей и приемной антенн , длина волны λ = 5 мм, длительность импульса 10 нс, период повторения импульсов T=0.3 мкс, угол наклона оси ДНА к оси ракеты , ширина ДНА _, величина относительной скорости ракеты и цели , скорость ракеты принята   м/с.

Расчет последовательности отраженных от ракеты "Гарпун" импульсов проводился для встречного курса ракеты и цели (рис. 3) при следующих параметрах условий встречи: . Траектория движения ракеты "Гарпун" в ОСК была задана в интервале координаты X={12..5} м, а шаг был выбран исходя из длительности импульса БРДЦ и значения относительной скорости . Кроме того, на рис. 3 приведена траектория пролета ракеты с БРДЦ над участком морской поверхности, причем ракета летит параллельно поверхности на высоте h=5 м. Длительность стробирующего импульса выбиралась исходя из диапазона дальностей от R₁=3 м до R₂=13 м. Предполагалось, что если дальность от БРДЦ до точки цели или поверхности не попадает в указанный диапазон, то отраженный сигнал принимается равным нулю.

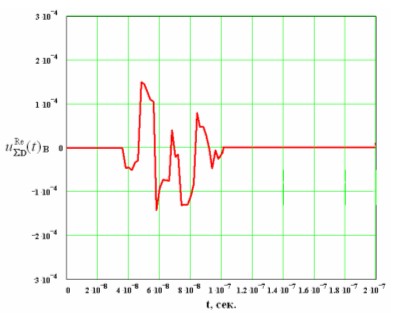
Рис. 4. Отсчеты напряжения импульса от цели «Гарпун» при значении координаты ее условной точки xц=12

Рис. 5. Отсчеты напряжения импульса от ракеты "Гарпун" и морской поверхности при значении координаты ее условной точки xц=12 м

 

 

На рис. 4 и 5 приведены реализации отраженных импульсов от ракеты «Гарпун» и от участка морской поверхности начальном участке траектории движения соответственно. В качестве примера при расчете отраженного импульса от ракеты «Гарпун» был выбран ракурс наблюдения, при котором условная точка цели находится в x=12 м, т.е. цель еще не попадает в диаграмму передатчика. Как видно из графиков, длительность отраженного импульса составляет величину порядка τ_отр.=22 нс для цели и τ_отр.=40 нс для поверхности, т.е. длительность импульса увеличилась, по сравнению с зондирующим. Увеличение длительности импульса обусловлено наличием дополнительных временных задержек от элементарных отражателей (ЭО), расположенных на разных дальностях. Величина задержки, на которую увеличивается длительность импульса составляет , где  - максимальная (минимальная) дальность от антенны до отдельных участков цели. В связи с тем, что длина ракеты «Гарпун» составляет 3.5 м, величина задержки, вычисленная по указанной выше формуле, соответствует значению, полученному в результате моделирования.

 

Рис. 6. Отсчеты мощности входного сигнала БРДЦ для двух типов зондирующих сигналов
(сплошные линии – отсчеты огибающей импульсов мощности, кресты – значения мощности отраженного сигнала при непрерывном зондирующем сигнале)

 

 

На рис. 6 приведены отсчеты огибающей импульсов мощности отраженного сигнала и соответствующие им значения мощности отраженного сигнала при непрерывном зондирующем сигнале. Как видно из графиков, максимальные значения огибающей отраженных импульсов могут быть как меньше, так и больше соответствующих им значений мощности при непрерывном сигнале. Этот факт может быть обусловлен, тем, что суммирование отраженных сигналов от различных ЭО при импульсном сигнале происходит в различные промежутки времени с учетом задержек и приводит к изменению характера интерференционной структуры сигналов от соседних ЭО.

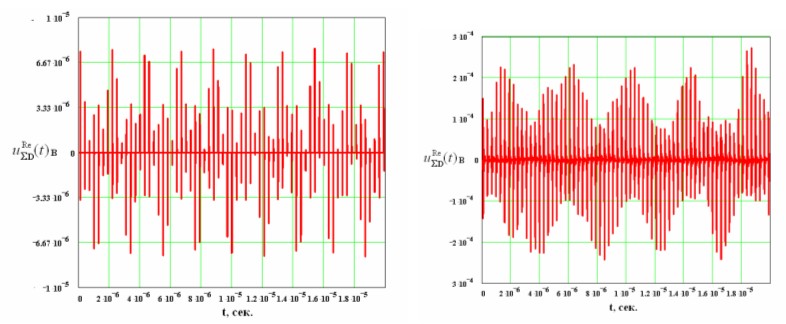
На рис. 7 приведены отсчеты огибающей импульсов квадратурного сигнала, принятого на траектории пролета от цели и от морской поверхности соответственно. Как видно из графиков, периодичность огибающей отраженного сигнала обусловлена эффектом Доплера. Соответственно для цели и поверхности период колебаний доплеровского сигнала существенно отличается, так как при приеме сигнала от поверхности доплеровская частота обусловлена только движением ракеты относительно цели, а при приеме отраженного сигнала от цели значение доплеровской частоты определяется относительной скоростью ракеты и цели.

 

Рис. 7. Реализация последовательности импульсов отраженных от ракеты "Гарпун" (слева) и от морской поверхности (справа) на начальном участке траектории относительного движения

 

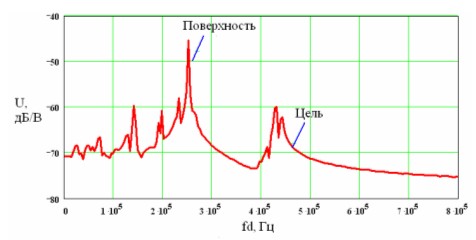
Различия в спектральных характеристиках доплеровских сигналов от цели и поверхности наглядно представлены на рис. 8, где приведена реализация спектра входного сигнала БРДЦ в полосе доплеровских частот при заданном значении интервала интегрирования сигнала во временной области. Полученные зависимости приведены

Рис. 8. Амплитудный спектр последовательности импульсов отраженных от ракеты "Гарпун" и морской поверхности в полосе доплеровских частот.

 

для случая, когда координата условной точки цели составляет =8 м. Для рис. 8 длительность интервала интегрирования при вычислении амплитудного спектра последовательности импульсов составляет 900 импульсов, т.е. . Как видно из графиков, при 900 накапливаемых импульсах разность значений между амплитудой полезного сигнала от цели и амплитудой сигнала от морской поверхности составляет 15 дБ, что позволяет значительно повысить вероятность обнаружения полезного сигнала от цели на фоне помехового сигнала от подстилающей поверхности. При 900 накапливаемых импульсах интервал наблюдения по координате X на траектории движения цели составляет соответственно . 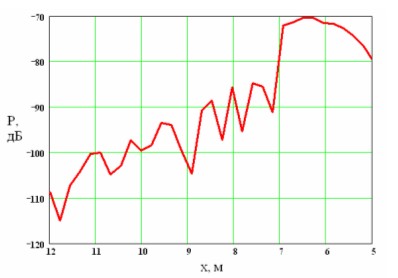В теории и практике проектирования БРДЦ принято значение среднеквадратичного отклонения координаты принятия решения принято равным , т.е. принятый интервал принятия решения о срабатывании не превышает среднеквадратичного отклонения КПР и соответственно не может существенно изменить характеристики эффективности БРДЦ. На рис. 9 приведены значения мощности отраженного сигнала с учетом накопления 900 импульсов в зависимости от координаты X условной точки цели соответственно. Как видно из графика, значения мощности отраженного сигнала увеличиваются при вхождении цели в пределы ДНА БРДЦ.

Рис. 9. График мощности отраженного от ракеты "Гарпун" сигнала на участке траектории движения цели

в диапазоне =12..5 м с учетом накопления 900 импульсов на каждом ракурсе.

 

Приемное устройство БРДЦ осуществляет бинарное (пороговое) обнаружение сигналов от цели, при котором средняя мощность входного сигнала на интервале наблюдения, рассчитанное по выражению, сравнивается с пороговым значением. Это значение определяется в соответствии с выбранным критерием обнаружения, обычно Неймана – Пирсона – характерным для радиолокационных систем. КС соответствует продольной координате Х в ОСК, при которой произошло обнаружение сигнала в приемном устройстве БРДЦ. В качестве примера для обеспечения принятия решения БРДЦ при вхождении цели в пределы ДНА пороговое значение мощности с учетом накопления 900 импульсов принято равным  дБ.

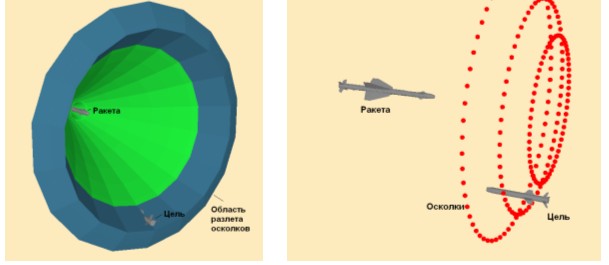
            На рис. 10 приведены схемы взаимного расположения ракеты и цели в моменты принятия решения БРДЦ, где показано расположение области эффективного действия средства доставки, когда центральный угол области эффективного действия составляет , а ширина области соответственно  (координата принятия решения БРДЦ составляет X=8.6 м). При этом как видно из графиков, большая часть контура цели попадает в область эффективного действия средства доставки.

 

 

Рис. 10. Схема взаимного расположения ракеты и цели в момент срабатывания БРДЦ

 

 

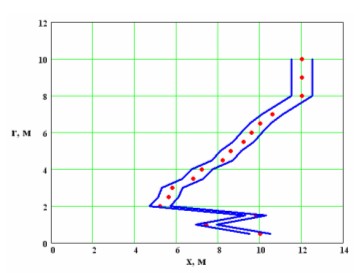
Рис. 11. Область принятия решений БРДЦ по ракете «Гарпун» в координатах {промах-координата x}

 

 

Максимальная эффективность средства доставки с БРДЦ достигается при согласовании ОПР с областью эффективного действия для каждого типа целей. Границы ОПР БРДЦ в сечении  по цели типа «Гарпун» приведены на рис. 11 в виде сплошных линий. Границы ОПР для каждого промаха определяются как , , где ,  – математическое ожидание и среднеквадратичное отклонение координаты принятия решения БРДЦ. В расчетах полагалось, что , представленные на рис. 11 в виде точек внутри ОПР, а значение  м определялось в результате статистического анализа результатов аналогичных испытаний. По результатам оценки ОПР БРДЦ в плоскости угла по трубке промахов  по ракете «Гарпун» получено предельное значение промаха  м и максимальное значение координаты принятия решения  м.

            Таким образом, в результате исследований, проведенных в статье можно сделать следующие выводы:

1. Математическая модель импульсного сигнала БРДЦ, отраженного от цели на основе ее многоточечной модели основана на представлении результирующего импульса цели в виде суперпозиции локальных импульсов, отраженных от элементарных отражателей с учетом временных задержек от передатчика и приемника БРДЦ, что позволяет проводить вычисления отраженных сигналов от целей при разнесенных в пространстве передающих и приемных системах.

2. Использование многоточечной модели цели позволяет проводить оценку ОПР импульсного БРДЦ в широком диапазоне условий встречи  для различных классов лоцируемых целей.

3. В результате математического моделирования последовательности отраженных от цели импульсов в типовых ситуациях пролета радиолокационной цели (ракета «Гарпун» и участок морской поверхности) относительно БРДЦ при малых промахах показано:

·        длительность отраженного импульса увеличивается по сравнению с излученным, на величину временной задержки, обусловленной прохождением импульса вдоль контура цели;

·        максимальные значения огибающей мощности отраженных импульсов могут быть как меньше, так и больше соответствующих им значений мощности при непрерывном сигнале, т.к. суммирование отраженных сигналов от различных отражателей при импульсном сигнале происходит в различные промежутки времени с учетом задержек и приводит к изменению характера интерференционной структуры сигналов от соседних отражателей;

·        с укорочением длительности зондирующего импульса происходит усиление флуктуаций напряжения в пределах одного отраженного импульса, что обусловлено скачками фазы при суммировании коротких импульсов по всем ЭО цели от импульса к импульсу.

3. Моделирование последовательности 900 импульсов на участке траектории относительного движения показало существенное разделение спектра доплеровских частот цели и подстилающей поверхности на 200 кГц.

Результаты исследований получены в процессе выполнения НИР по проекту «Проведение поисковых научно-исследовательских работ по направлению «Радиофизика, акустика и электроника» в рамках мероприятия 1.2.2 Программы», выполняемому в рамках мероприятия 1.2.2 «Проведение научных исследований научными группами под руководством кандидатов наук» направления 1 «Стимулирование закрепления молодежи в сфере науки, образования и высоких технологий» федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы.

 

Литература

1.     Борзов А.Б., Соколов А.В., Сучков В.Б. Цифровое моделирование входных сигналов систем ближней радиолокации от сложных радиолокационных сцен. // Успехи современной радиоэлектроники, 2004.- № 9-10. - С. 38-61.

2.     Борзов А.А., Борзов А.Б., Сучков В.Б. Многоточечная модель радиолокационной цели в задачах синтеза входных сигналов радиовзрывателей. Оборонная техника, 2007, № 3-4.