УДК 519,688
Карты Кохонена как способ восстановления мультимедийной информации
И. Б. Ларионов
Омский государственный университет им. Ф.М.Достоевского
Получена 4 октября 2010 г., после доработки 12 октября 2010 г.
Аннотация. Разработана модель восстановления мультимедийной информации с использованием карт Кохонена на примере графических изображений. Показано, что данная модель имеет преимущество перед традиционными методами.
Ключевые слова: восстановление изображений, нейронные сети, карты Кохонена, мультимедиа.
Введение
В ходе работы над методами восстановления изображений был рассмотрен способ восстановления изображений с использованием сингулярного разложения матриц с пропусками. Как показано в работах [1, 2], этот метод позволяет восстанавливать изображения, однако, в определенных случаях ошибка восстановления настолько велика, что использование этого метода становится сомнительным. В данной работе мы рассмотрим метод восстановления поврежденных изображений с использованием самоорганизующихся карт Кохонена [3].
Самоорганизующиеся карты Кохонена
Карта Кохонена состоит из набора нейронов, количество которых задается аналитиком. Каждый нейрон, в свою очередь, описывается двумя векторами:
1. Вектор
веса нейрона ![]() .
В общем случае, размерность вектора совпадает с размерностью векторов входных
данных.
.
В общем случае, размерность вектора совпадает с размерностью векторов входных
данных.
2. Вектор
координат ![]() . В
общем случае, вектор
. В
общем случае, вектор ![]() описывает
точку в пространстве, в которой расположен нейрон.
описывает
точку в пространстве, в которой расположен нейрон.
Обычно нейроны располагают на плоскости в вершинах регулярной решетки с квадратными либо шестиугольными ячейками.
Инициализация карты Кохонена
Существуют
несколько способов начальной инициализации карты, путем присвоения значений всем
векторам весов нейронов ![]() следующими способами:
следующими способами:
1. Задание всех координат случайными числами.
2. Присвоение вектору веса значения случайного наблюдения из входных данных.
3. Выбор векторов веса из линейного пространства, натянутого на главные компоненты набора входных данных.
Следует
заметить, что каждый нейрон после инициализации становится неподвижен на карте,
т.е. вектор ![]() не
изменяется в течение всего обучения.
не
изменяется в течение всего обучения.
Алгоритм обучения
Алгоритм обучения производится по итерациям [3].
Пусть ![]() - номер итерации.
Положим, что инициализация имела номер итерации
- номер итерации.
Положим, что инициализация имела номер итерации ![]() . Далее, выполняются следующие операции:
. Далее, выполняются следующие операции:
1. Выбираем
случайный вектор ![]() из
набора входных значений.
из
набора входных значений.
2. Находим
расстояния до всех векторов весов всех нейронов карты. Для данной операции
выбирается какая-нибудь мера, в общем случае, среднеквадратическое отклонение.
Ищем нейрон, наиболее близкий ко входному значению ![]() :
:
![]()
где ![]() - вектор
веса нейрона победителя (MBU, Winner)
- вектор
веса нейрона победителя (MBU, Winner) ![]() ,
,
![]() - вектор веса
- вектор веса
![]() -го узла в
карте,
-го узла в
карте,
![]() - некая мера
отклонения.
- некая мера
отклонения.
В случае, если вышеуказанному условию удовлетворяет несколько нейронов, BMU
выбирается случайным образом.
3. Определение меры соседства нейронов и изменение весов нейронов в карте
a. Выбираем
меру соседства - функцию ![]() :
:
Эта функция определяет <<меру соседства>> между нейронами ![]() и
и ![]() . Обычно, в качестве функции
. Обычно, в качестве функции ![]() используется
гауссовская функция:
используется
гауссовская функция:
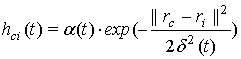 ,
,
где ![]() —
обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то
есть определяющий приближение значения векторов веса BMU и его соседей к
наблюдению; чем больше шаг, тем меньше уточнение);
—
обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то
есть определяющий приближение значения векторов веса BMU и его соседей к
наблюдению; чем больше шаг, тем меньше уточнение);
![]() ,
, ![]() — координаты узлов
— координаты узлов ![]() и
и ![]() на карте;
на карте;
![]() —
сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает.
—
сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает.
Параметры ![]() ,
, ![]() и их характер убывания
задаются аналитиком.
и их характер убывания
задаются аналитиком.
Более простой способ задания функции соседства:
![]()
если ![]() находится
в окрестности
находится
в окрестности ![]() заранее
заданного аналитиком радиуса, и 0 в противном случае.
заранее
заданного аналитиком радиуса, и 0 в противном случае.
Функция ![]() )
равна
)
равна ![]() для BMU
и уменьшается с удалением от BMU.
для BMU
и уменьшается с удалением от BMU.
b. Вычисление
ошибки карты
Изменяем вектора весов по формуле:
![]() .
.
Таким образом, все узлы, являющиеся соседями BMU, приближаются к
рассматриваемому наблюдению.
4. Выбор
остановочного условия.
Для определения критерия остановки в большинстве случаев используется ошибка
карты, например, как среднее арифметическое расстояние между наблюдениями и
векторами веса соответствующих им BMU:
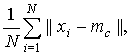
где ![]() -
количество элементов набора входных данных.
-
количество элементов набора входных данных.
Исходя из написанного выше, можно выделить следующие элементы для моделирования системы восстановления мультимедийных данных:
1. ![]() - вектор наблюдаемых
данных. В применении к восстановлению мультемидийной информации это может быть
какой-то набор пикселей (сэмплов, набор блоков сжатия изображений),
сгруппированных по определенному правилу.
- вектор наблюдаемых
данных. В применении к восстановлению мультемидийной информации это может быть
какой-то набор пикселей (сэмплов, набор блоков сжатия изображений),
сгруппированных по определенному правилу.
2. ![]() - вектор веса нейрона.
По определению, должен быть одной размерности с
- вектор веса нейрона.
По определению, должен быть одной размерности с ![]() .
.
3. ![]() - мера соседства
нейронов. Некоторая функция, возвращающая расстояние между нейронами и зависящая
от номера итерации
- мера соседства
нейронов. Некоторая функция, возвращающая расстояние между нейронами и зависящая
от номера итерации ![]() .
При определенных условиях может определять и топологию поверхности, на которую
нанесена карта.
.
При определенных условиях может определять и топологию поверхности, на которую
нанесена карта.
4. ![]() - мера отклонения,
показывающая, насколько вектор
- мера отклонения,
показывающая, насколько вектор ![]() не "похож" на вектор
не "похож" на вектор ![]() .
.
Таким образом, если в некоторой модели определены вышеуказанные элементы, то в этой модели можно использовать самоорганизующиеся карты Кохонена для восстановления поврежденных участков данных.
Построение модели на примере графических изображений
В данном разделе будут описаны меры и методы построения векторов данных для графических изображений. В общем случае, изображение, представленное в цифровом виде является набором пикселей (точек изображения). В общем случае (за исключением экзотических форматов, имеющих исчезающе малое применение), изображение является прямоугольным и характеризуется шириной в пикселях, высотой в пикселях и количеством значений, которое каждый пиксель может принимать (глубина палитры, зачастую измеряется в битах, отведенных на один пиксель) [4]. Так же, изображение характеризуется методом сжатия (если таковой используется), но в данной работе это не будет рассматриваться.
Вектор наблюдаемых данных
Рассмотрим
способ приведения набора пикселей изображения к векторному виду.
В силу того, что изображение является прямоугольным, и глаз воспринимает не отдельные точки, а некоторую совокупность, следует рассматривать не последовательный набор пикселей, а некоторую совокупность, сгруппированную вокруг определенной, заранее выбранной точки.
Кроме того, палитра, как набор значений цветов, не удовлетворяет модели с поврежденными пикселями, поэтому необходимо ее расширить, путем добавления цвета поврежденного значения.
Для дальнейшего исследования, введем следующие понятия и обозначения:
· Пиксель - номер цвета из палитры изображения, отвечающий соответствующей точке на изображении,
· Поврежденный пиксель - отсутствие номера цвета из палитры изображения, соответствующего точке на изображении, в силу повреждения данной точки,
·
![]() -
палитра исходного изображения. В общем случае,
-
палитра исходного изображения. В общем случае, ![]() ,
,
·
![]() -
цвет, соответствующий поврежденному пикселю,
-
цвет, соответствующий поврежденному пикселю,
·
![]() -
расширенная палитра, содержащая в себе цвет поврежденного пикселя,
-
расширенная палитра, содержащая в себе цвет поврежденного пикселя,
·
![]() -
-
![]() -я компонента
вектора
-я компонента
вектора ![]() ,
,
·
![]() -
количество столбцов исходного изображения (ширина изображения в пикселях),
-
количество столбцов исходного изображения (ширина изображения в пикселях),
·
![]() -
количество строк исходного изображения (высота изображения в пикселях),
-
количество строк исходного изображения (высота изображения в пикселях),
·
![]() -
пиксель, расположенный в
-
пиксель, расположенный в ![]() -том столбце и
-том столбце и ![]() -той строке на изображении,
-той строке на изображении,
·
![]() -
восстановленное значение пикселя расположенного в
-
восстановленное значение пикселя расположенного в ![]() -том столбце и
-том столбце и ![]() -той строке на изображении,
-той строке на изображении,
·
![]() -
целая часть деления
-
целая часть деления ![]() на
на
![]() с остатком,
с остатком,
·
![]() -
остаток от деления
-
остаток от деления ![]() на
на
![]() ,
,
·
![]() -
ширина карты в нейронах,
-
ширина карты в нейронах,
·
![]() -
высота карты в нейронах,
-
высота карты в нейронах,
·
![]() -
количество нейронов в карте.
-
количество нейронов в карте.
·
![]() -
горизонтальная координата местоположения нейрона
-
горизонтальная координата местоположения нейрона ![]() ,
,
·
![]() -
вертикальная координата местоположения нейрона
-
вертикальная координата местоположения нейрона ![]() .
.
В ходе построения подели был выбран следующий способ построения вектора значений из блока пикселей:
![]()
![]()
![]()
где ![]() - размер блока, принятый в модели,
- размер блока, принятый в модели, ![]() - координаты пикселя,
для которого строится вектор наблюдения.
- координаты пикселя,
для которого строится вектор наблюдения.
Соответственно, при использования описанного метода построения векторов, необходимо учитывать следующие ограничения:
·
![]() должно
удовлетворять требованию
должно
удовлетворять требованию ![]() ,
,
·
![]() должно
удовлетворять требованию
должно
удовлетворять требованию ![]() ,
,
·
![]() должно
быть нечетным.
должно
быть нечетным.
Первые два условия вводятся в силу того, что размер рассматриваемого блока больше одного пикселя и, соответственно, количество таких блоков будет меньше, чем количество пикселей в изображении.
Второе условие накладывается для более точного описания окружности пикселя, а именно для симметричности окружности пикселя.
Мера соседства нейронов
Мера соседства
нейронов ![]() представляет
собой функцию от индексов нейронов и номера итерации. Для простоты изложения и применения
в дальнейшем, представим ее в следующем виде:
представляет
собой функцию от индексов нейронов и номера итерации. Для простоты изложения и применения
в дальнейшем, представим ее в следующем виде:
![]()
где ![]() - некоторая, заданная
исследователем функция,
- некоторая, заданная
исследователем функция, ![]() - индекс первого нейрона,
- индекс первого нейрона, ![]() - индекс второго
нейрона,
- индекс второго
нейрона, ![]() -
номер итерации.
-
номер итерации.
В ходе исследования, было принято решение использовать видоизмененную функцию Гаусса:
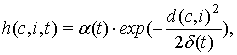 (1)
(1)
где ![]() имеет вид:
имеет вид:
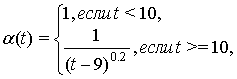 (2)
(2)
![]() имеет вид
имеет вид
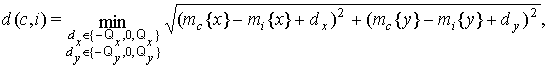 (3)
(3)
![]() имеет вид
имеет вид
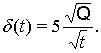 (4)
(4)
Функция (2) на первых 9 итерациях имеет значение 1. Это сделано для того, что бы максимально равномерно инициализировать карту в начале обучения. Причины такого решения будут описаны ниже.
Функция (3) в приведенном виде будет возвращать расстояние между нейронами так, как будто карта натянута на тороидальную поверхность. Причины такого решения будут описаны ниже.
Функция (4) приведена к такому виду в ходе экспериментов по обучению карт.
Мера отклонения
В работе [2] были рассмотрены 4 метрики применительно к определению качества восстановления изображений. Любая из описанных метрик может быть использована в картах Кохонена.
В ходе данной
работы, была выбрана среднеквадратическая ошибка как наиболее простая в
вычислении. Таким образом, ![]() имеет следующий вид:
имеет следующий вид:
![]() (5)
(5)
Практическая реализация карт Кохонена для восстановления изображений
В ходе работы был реализован программный комплекс KohonenMapRestore. В данный комплекс входят:
1. Модуль загрузки и приведения изображений различных форматов ко внутреннему формату программного комплекса,
2. Интерфейс с возможностью выделения поврежденных областей изображения,
3. Модуль нейросети, реализующий функциональность карт Кохонена,
4. Модуль сохранения и загрузки состояния карты в файл,
5. Модуль оценки качества восстановления, в котором реализованы следующие метрики:
a. метрика Минковского,
b. среднеквадратическая ошибка,
c. метрика разницы с соседями,
d. метрика многомерного расстояния.
Особенности реализации
Так как целью работы было выявление возможности восстановления графической информации с использованием самоорганизующихся карт Кохонена и оценка качества такого восстановления, все объекты в программном комплексе проектировались максимально универсально.
Интерфейс
Интерфейс программы состоит из следующих элементов:
Графическая область, в которой можно показать как изображение, так и саму карту. Так же при отображении изображения можно отмечать поврежденные участки изображения.
1. Текстовое поле с местоположением файла с изображением.
2. Кнопка "loadImage", при нажатии на которую в память приложения загружается указанное в поле ввода изображения и преобразуется во внутренний формат программы.
3. Кнопка "Show Image", при нажатии на которую, в графической области отображается загруженное в данный момент изображение.
4. Кнопка "show Map", при нажатии на которую в графической области отображается текущее состояние карты.
5. Кнопка "Learn", нажатие на которую инициализирует процесс обучения.
6. Кнопка "Restore", нажатие на которую инициализирует процесс восстановления изображения.
7. Чекбокс "Continue", который отмечен в процессе обучения. Если в процессе обучения снять галочку, то алгоритм остановится и можно будет производить восстановление изображения на не до конца обученной карте.
8. Контекстное меню при отображении карты позволяет сохранять и загружать состояние карты из файла.
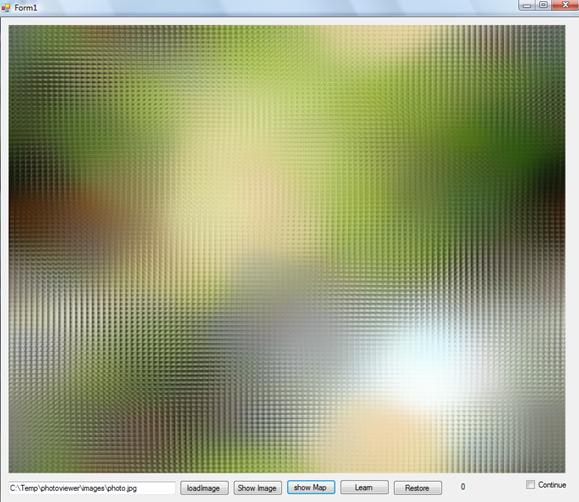
Рис. 1 Интерфейс
Нейрон
По определению, нейрон обладает следующими характеристиками:
· вектор веса,
· вектор местоположения на карте.
Для максимальной универсальности, вектор веса был реализован как абстрактный объект, а вектор местоположения - как координаты на плоскости. Такая реализация позволяет использовать векторы весов любой размерности.
Мера соседства
В силу того, что было принято решение размещать карту на координатной сетке размерности 2, мера соседства была выбрана как евклидово расстояние на плоскости.
Однако, в ходе
экспериментов было замечено, что при попадании BMU в угол координатной сетки
(например:![]() ,
, ![]() ), количество нейронов,
которые подвергаются изменению при обучении уменьшается в 4 раза по сравнению с
ситуацией, когда BMU попадает в центр карты (
), количество нейронов,
которые подвергаются изменению при обучении уменьшается в 4 раза по сравнению с
ситуацией, когда BMU попадает в центр карты (![]() ).
).
Из-за этого было принято решение о введении меры соседства, которая бы нивелировала такую проблему, а именно, использование меры соседства вида 3. Такое решение позволило избежать проблемы попадания на край карты и максимизировать воздействие обучения.
Функция (4) приведена к такому виду в хоте проведения экспериментов на различных размерах карты. Такой вид функции позволил максимизировать воздействие на нейроны на начальных итерациях вне зависимости от количества нейронов.
Функция (2) приведена к такому виду для простоты описания процесса инициализации. Первые 10 итераций являются инициализацией и в ходе этих шагов не происходит поиск BMU. Номера нейронов на этом этапе задаются явно и расположены максимально равномерно по всей карте.
Таким образом, все приведенные выше меры позволили максимально упростить изменение размеров карты при проведении экспериментов и создать наиболее универсальную процедуру инициализации карты.
Процесс обучения
Изначально все
веса нейронов выставляются в нулевые значения (что соответствует черному цвету
в палитре ![]() ).
).
Первые 10 итераций, как и было описано ранее, являются итерациями инициализации. Из изображения выбираются 10 блоков. Несущие максимальное количество информации, т.е. удовлетворяющие условию:
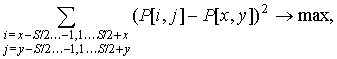
![]()
![]()
Для этих блоков производится обучение карты. При этом местоположение BMU жестко заданы, а именно - равномерно распределены по карте. Это делается для того, что бы изначально карта несла максимальное количество информации из изображения.
На каждой
последующей итерации случайным образом выбирается пара координат ![]() таким образом, что бы
выполнялись следующие условия:
таким образом, что бы
выполнялись следующие условия:
![]()
![]()
![]()
Т.е. из исходного изображения
выбираются случайные блоки размером ![]() пикселей, ни один из которых не является
поврежденным.
пикселей, ни один из которых не является
поврежденным.
Критерий остановки алгоритма
Для остановки обучения можно ввести несколько критериев:
1. Относительно малое изменение карты при обучении на очередной итерации,
2. Исчерпание всех возможных наборов векторов наблюдаемых данных.
В первом
случае, за критерий остановки было принято условие, при котором ни один из
векторов весов нейронов ни в одной из своих компонент не изменил номер цвета.
Т.е. ![]() .
.
Восстановление изображения
После остановки процесса обучения можно приступать к самой процедуре восстановления.
Восстановление производится итерационно, как и обучение. При восстановлении из наборов векторов наблюдаемых данных выбирается случайный вектор, в котором поврежденным является только один пиксель.
Для данного вектора ищется BMU, однако метрика поиска в этом случае изменяется:
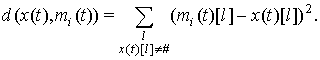
Таким образом из всех векторов весов выбирается наиболее "похожий", без учета компоненты, соответствующей поврежденному пикселю.
После того, как BMU найден, поврежденный пиксель на изображении заменяется на соответствующий из вектора веса нейрона.
Данная процедура повторяется до тех пор, пока на исходном изображении не будет ни одного поврежденного пикселя.
Сохранение и загрузка карты
Данная функциональность реализована для возможности восстановления по карте, обученной на множестве изображений. В качестве формата файла была выбрана структура XML, которая позволяет хранить сложные структуры в текстовом формате.
Программная реализация
В качестве платформы для реализации программного комплекса KohonenMapRestore была выбрана платформа .Net и язык C#, т.к. этот язык позволяет легко оперировать абстрактными объектами и типами данных.
Кроме того, такой выбор средств реализации позволил сделать удобным выбор метрик, размера блока окружности пикселя, а так же выбор меры соседства из интерфейса приложения.
Оценка качества восстановления изображений с использованием карт Кохонена
Для оценки качества восстановления было произведено сравнение данного метода с методом восстановления изображений с использованием интерполяции бикубическими сплайнами, т.к. этот метод показал хорошие результаты в работе [2].
Для более точной оценки производилось 100 испытаний для каждого из 20 изображений при 3-х различных степенях повреждений:
1. Поврежден один пиксель,
2. Повреждены 100 одиночных пикселей в различных местах изображения,
3. Повреждена
область 8![]() 32
пикселей.
32
пикселей.
Изображения можно условно разделить на 4 группы:
1. Высококачественные фотографии NASA,
2. Высококачественные фотографии пейзажей,
3. Фотографии групп людей,
4. Различные искусственные изображения - логотипы, векторная графика, фрактальные изображения, которые были преобразованы в формат BMP.
Каждое испытание проводилось на новой карте поврежденных пикселей. Данная карта наносилась на изображение для обоих методов восстановления, т.о. оценивалось восстановление каждого конкретного случая двумя способами.
Для вычисления ошибки использовалось среднее квадратичное отклонение [4].
Размер блока ![]() был принят за 7.
был принят за 7.
С примерами поврежденных и восстановленных изображений можно ознакомиться в приложении 1.
Результаты испытаний приведены в Таблице 1 (результат в отдельной группе взят как среднее арифметическое всех испытаний этой группы).
Таблица 1: Результаты испытаний
|
Повреждение |
1 |
2 |
3 |
|||
|
Метод |
Спл. |
Карта |
Спл. |
Карта |
Спл. |
Карта |
|
Высококачественные фотографии NASA |
246,51 |
2,12 |
6345,20 |
352,65 |
94234,85 |
43732,25 |
|
Высококачественные фотографии пейзажей |
345,02 |
3,18 |
9437,69 |
395,49 |
105681,44 |
46226,66 |
|
Фотографии групп людей |
234,76 |
3,93 |
4753,29 |
426,76 |
97565,38 |
67159,14 |
|
Искусственные изображения |
96,45 |
1,02 |
2387,65 |
150,19 |
93517,95 |
55365,59 |
Как видно из таблицы, метод восстановления с использованием карт Кохонена стабильно показывает лучшие результаты, чем метод с бикубическими сплайнами. Стоит заметить, что при некоторых экспериментах в первой группе повреждений карты Кохонена выдавали нулевую ошибку, т.е. абсолютно точно восстанавливали поврежденный пиксель, в то время, как метод с бикубическими сплайнами ошибался в этом же эксперименте на 3-4 оттенка в палитре.
Выводы
В ходе проведенной работы был выявлен большой потенциал карт Кохонена как инструмента для восстановления поврежденных мультимедийных данных. В некоторых случаях карты Кохонена восстанавливали одиночный поврежденный пиксель с нулевой ошибкой, что не получилось у метода с бикубическими сплайнами.
Однако, у карт
Кохонена был выявлен недостаток при восстановлении блоков поврежденных
пикселей, выражающийся в накоплении ошибки восстановления от окраин
поврежденного блока к центру. В ходе экспериментов было выявлено, что это
вызвано размером блока ![]() , который был недостаточно велик для
качественного восстановления. Но даже при таком недостатке карты Кохонена
показали более хорошие результаты, нежели восстановление с использованием
бикубических сплайнов.
, который был недостаточно велик для
качественного восстановления. Но даже при таком недостатке карты Кохонена
показали более хорошие результаты, нежели восстановление с использованием
бикубических сплайнов.
При увеличении
размера ![]() до
максимального размера поврежденного блока, накоплении ошибки было значительно
уменьшено, что заставляет проводить исследование зависимости соотношения
максимального размера поврежденного блока и размера блока
до
максимального размера поврежденного блока, накоплении ошибки было значительно
уменьшено, что заставляет проводить исследование зависимости соотношения
максимального размера поврежденного блока и размера блока ![]() к качеству восстановления изображения.
к качеству восстановления изображения.
Литература
1. Горбань А.Н., Макаров С.В., Россиев А.А. Итерационный метод главных компонент для таблиц с пробелами // Третий сибирский конгресс по прикладной и индустриальной математике (ИНПРИМ-98), 22-27 июня 1998. Тезисы докладов. Ч.5. Новосибирск: Изд-во Института математики СО РАН, 1998.
2. Ларионов И.Б. Кластеризация матриц с пропусками как метод восстановления графической информации // Математические структуры и моделирование, 2009, вып. 20, с. 97-106.
3. T. Kohonen Self-organizing Maps - 3 ed. - Berlin, Heidelberg, New York, Barcelona, Hong Kong, London, Milan, Paris, Singapore, Tokio, Springer, 2001.
4. Ismail Avcibas, Ismail Avcibas, Bulent Sankur, Lale Akarun, Emin Anarim, Nasir Memon, Yucel Yemez Image Quality Statistics and Their Use in Steganalysis and Compression, Istanbul, 2001
Приложение 1
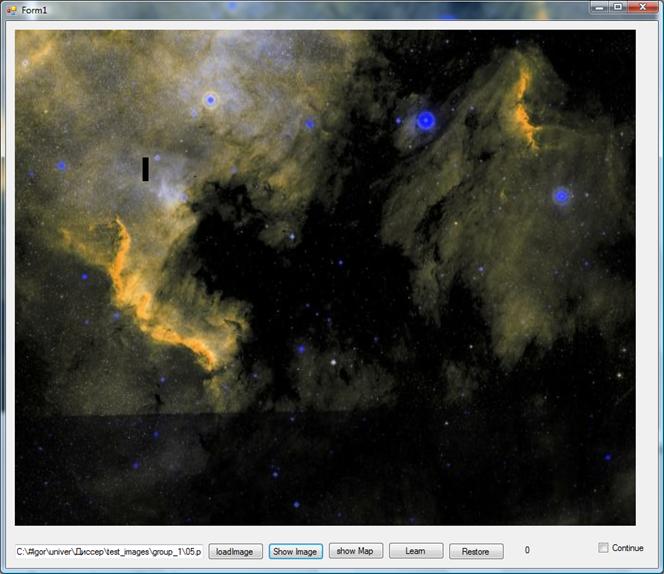
Рис. 2 Фотография NASA. Блок 8х32 пикселя.

Рис. 3 Фотография NASA. Восстановление бикубическими сплайнами.
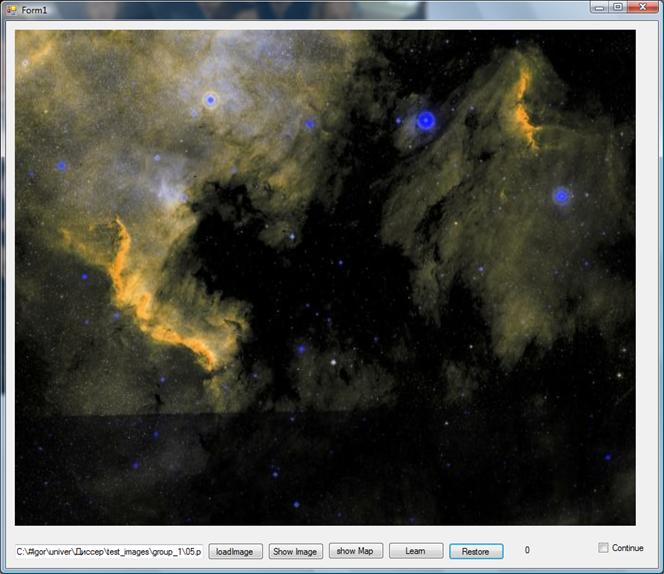
Рис. 4 Фотография NASA. Восстановление картами Кохонена.
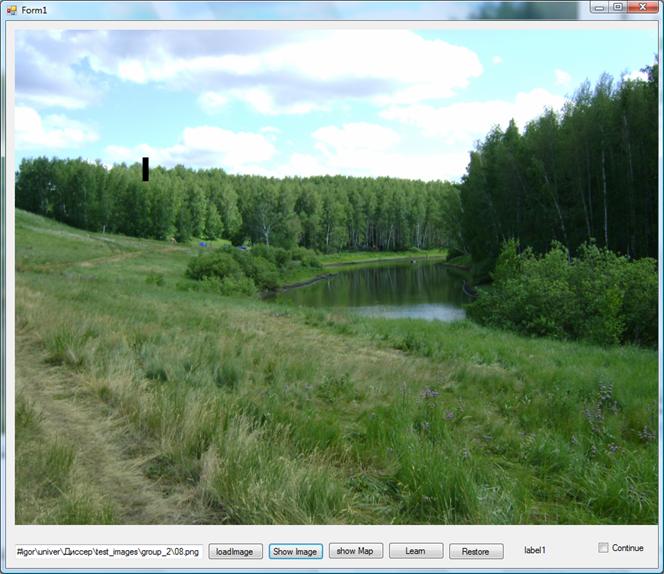
Рис. 5 Пейзаж. Блок 8х32 пикселей.
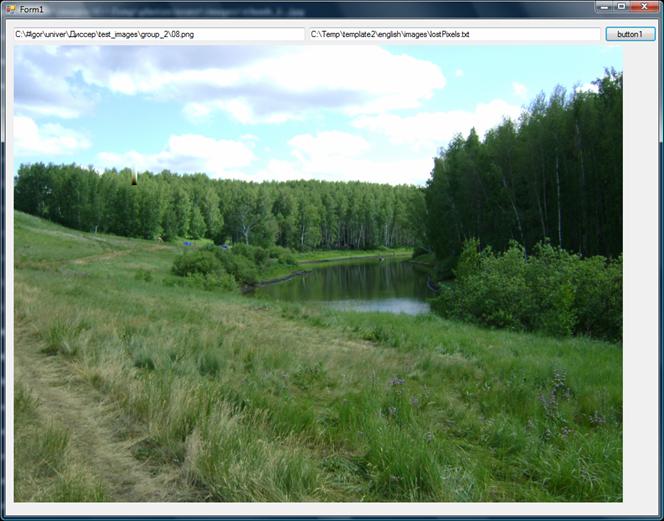
Рис. 6 Пейзаж. Восстановление бикубическими сплайнами.
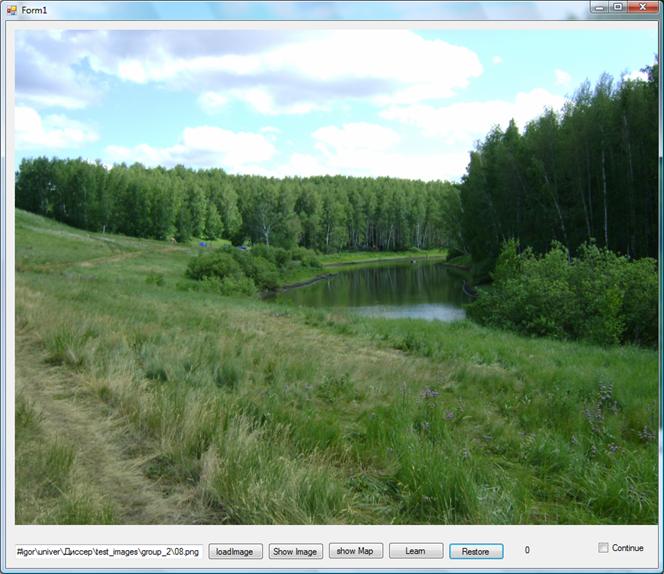
Рис. 7 Пейзаж. Восстановление картами Кохонена.
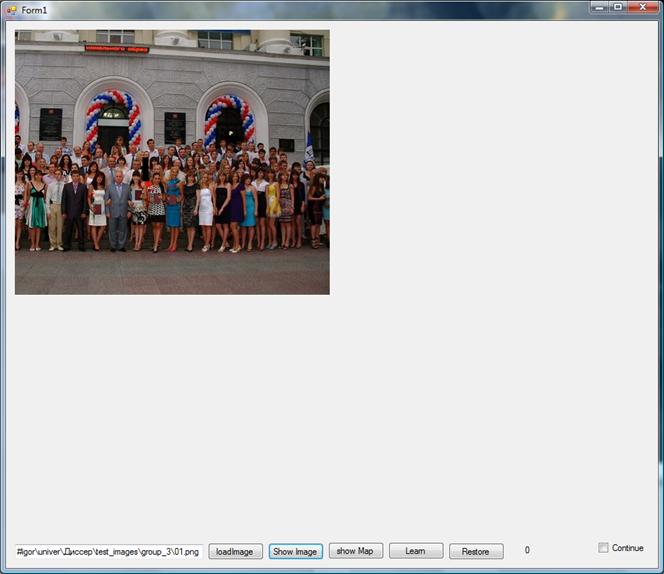
Рис. 8 Фотография группы людей. Блок 8х32 пикселей.
Рис. 9 Фотография группы людей. Восстановление бикубическими сплайнами.
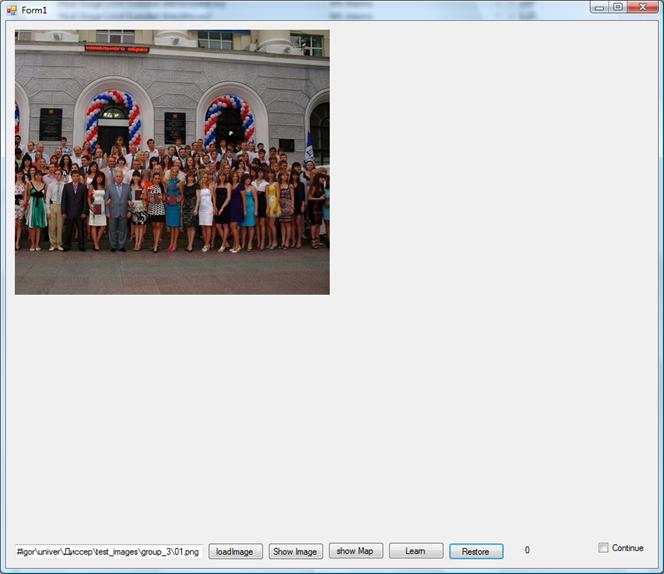
Рис. 10 Фотография группы людей. Восстановление картами Кохонена.
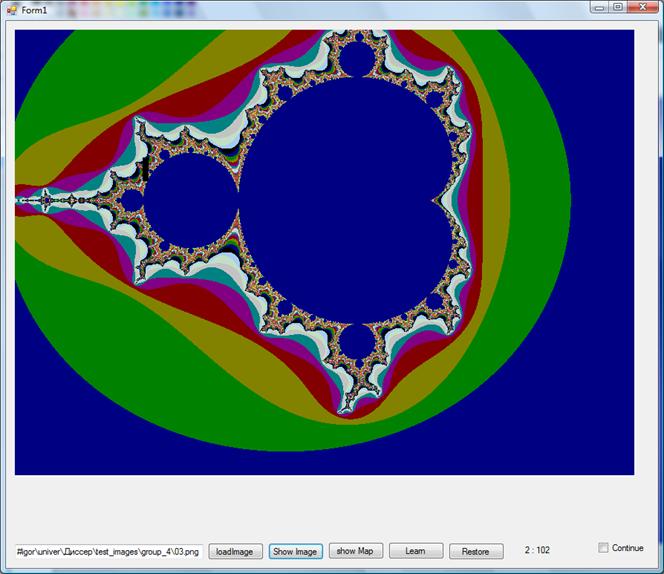
Рис. 11 Фрактал. Блок 8х32 пикселей.
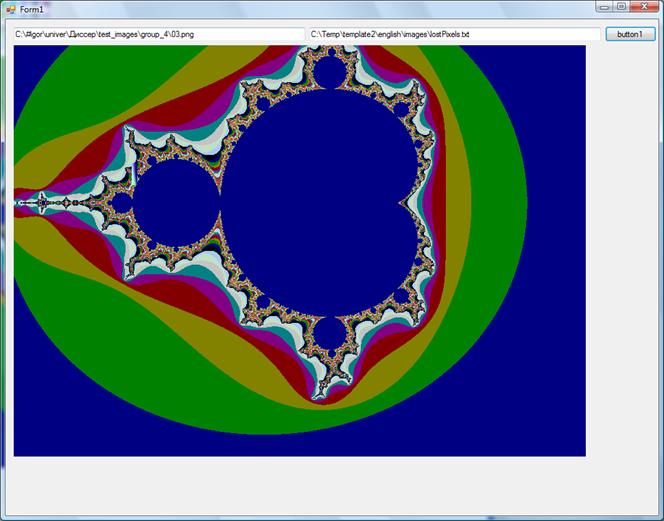
Рис. 12 Фрактал. Восстановление бикубическими сплайнами.
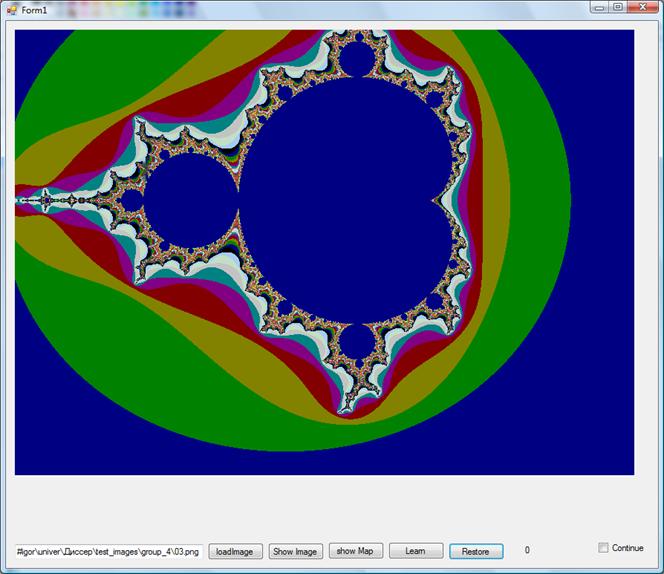
Рис. 13 Фрактал. Восстановление картами Кохонена.