УДК 621.396.96
Требование к точности задания траектории носителя РСА при имитации эхо-сигнала от поверхностно-распределенного объекта
Р. Ю. Белоруцкий, А. В. Киселев
Новосибирский государственный технический университет
Получена 26 сентября 2011 г.
Аннотация. Рассмотрен вопрос имитации эхо-сигналов от земной поверхности при работе РЛС в режиме картографирования с синтезированием апертуры антенны. Получены аналитические соотношения для оценки смещения отметки от точечного отражателя на радиолокационном изображении в результате неточности задания моделируемой траектории носителя РЛС.
Ключевые слова: имитационное моделирование эхо-сигналов, радиолокация, синтезирование апертуры.
Abstract. The simulation of echo signals reflected from the Earth surface for mapping mode of synthetic aperture radar is considered. The analytical expressions for estimating point reflector pip displacement on radar image as a result of inaccuracy in setting the modeled SAR sensor trajectory are obtained.
Keywords: radar echo simulation modeling, radiolocation, aperture synthesis.
Введение
Ввиду сложности и больших материальных затрат на натурные испытания на этапах проектирования, отладки, отработки режимов работы радиолокационных станций получило распространение проведение полунатурных экспериментов [1]. В этом случае в лабораторных условиях производится моделирование радиолокационной обстановки путем подачи на вход приемника РЛС соответствующих сигналов и помех. Технически это осуществляется с помощью специальных аппаратно-программных средств – имитаторов. Как правило, они формируют отсчеты комплексной огибающей имитируемого сигнала, потом преобразуют их в аналоговый сигнал и переносят в область рабочих частот РЛС. Например, в случае радиолокационных систем дистанционного зондирования Земли (ДЗЗ) они должны адекватно имитировать эхо-сигналы, отражаемые от поверхности и, в результате, формировать радиолокационное изображение (РЛИ) местности.
Наибольшую сложность в реализации аппаратно-программных средств при имитации представляет собой формирование отсчетов имитируемых сигналов и помех. Они должны формироваться в реальном масштабе времени (РМВ) с учетом текущих параметров моделируемой ситуации (параметров зондирующих сигналов РЛС, положения и скорости носителя на моделируемой траектории и др.).
Высокая разрешающая способность радиолокационных станций с синтезированной апертурой (РСА), используемых в системах ДЗЗ, устанавливает жесткие требования по соответствию имитируемых сигналов реальным эхо-сигналам. Большинство объектов на радиолокационных изображениях, получаемых РСА, обладают сложной многоточечной структурой. При имитации эхо-сигнал от сложного объекта представляется совокупностью сигналов от элементарных точечных отражателей [1]. При этом комплексная огибающая входного сигнала РЛС формируется как сумма сигналов от отдельных независимых точечных отражателей в координатах, соответствующих РЛИ:
где ![]() и
и ![]() – амплитуда и текущая фаза эхо-сигнала от
i-го отражателя;
– амплитуда и текущая фаза эхо-сигнала от
i-го отражателя;
![]() – комплексная огибающая зондирующего
сигнала;
– комплексная огибающая зондирующего
сигнала; ![]() – время задержки сигнала, отраженного от i-го
отражателя; N –
количество точек, формирующих РЛИ.
– время задержки сигнала, отраженного от i-го
отражателя; N –
количество точек, формирующих РЛИ.
Сигналу от каждого отражателя соответствуют свои функции изменения задержки и фазы во времени.
Отсчеты сигнала имитатора
должны представлять собой дискретизированную во времени комплексную огибающую ![]() .
.
Реализация (1) обеспечивает высокую степень соответствия реальному эхо-сигналу, но при высоком разрешении требует огромных вычислительных ресурсов. Это существенно ограничивает возможность непосредственного использования (1) для формирования отсчетов имитируемого сигнала в РМВ.
С целью снижения вычислительных
затрат в [2] предложен следующий способ формирования отсчетов комплексной
огибающей сигнала. До начала имитации согласно (1) рассчитываются отсчеты
комплексной огибающей сигнала для зондируемого участка поверхности и некоторой
предполагаемой траектории носителя. Из ![]() устраняется
набег фазы и задержка сигнала от центральной точки участка (назовем её опорной):
их значения вычитаются из текущих значений фаз и задержек сигналов от каждого
эквивалентного отражателя, образующих участок поверхности. Таким образом,
получается сигнал, сохраняющий информацию о фазовых и временных соотношениях,
присущих эхо-сигналу от поверхности. Во время имитации вводится операция его преобразования
в имитируемый эхо-сигнал. В процессе моделируемого полета носителя РЛС точно
рассчитываются и устанавливаются текущие значения задержки и фазового сдвига
сигнала для центральной точки участка. При этом для остальных точек они
меняются пропорционально значению от опорной согласно взаимосвязям в исходном
сигнале. Эта процедура призвана свести к минимуму количество вычислений: из
расчетов в РМВ исключается сложный расчет законов изменения фаз
устраняется
набег фазы и задержка сигнала от центральной точки участка (назовем её опорной):
их значения вычитаются из текущих значений фаз и задержек сигналов от каждого
эквивалентного отражателя, образующих участок поверхности. Таким образом,
получается сигнал, сохраняющий информацию о фазовых и временных соотношениях,
присущих эхо-сигналу от поверхности. Во время имитации вводится операция его преобразования
в имитируемый эхо-сигнал. В процессе моделируемого полета носителя РЛС точно
рассчитываются и устанавливаются текущие значения задержки и фазового сдвига
сигнала для центральной точки участка. При этом для остальных точек они
меняются пропорционально значению от опорной согласно взаимосвязям в исходном
сигнале. Эта процедура призвана свести к минимуму количество вычислений: из
расчетов в РМВ исключается сложный расчет законов изменения фаз ![]() и задержек
и задержек ![]() парциальных
сигналов в составе имитируемого эхо-сигнала, а также выполнение расчета (1).
парциальных
сигналов в составе имитируемого эхо-сигнала, а также выполнение расчета (1).
Практическому использованию рассматриваемого способа препятствует то, что траектория носителя при проведении эксперимента может отличаться от предполагаемой, или начало синтезирования апертуры может начинаться в иной её точке, нежели предполагалось заранее. При этом возникает проблема, состоящая в отклонении задаваемого положения носителя РЛС при формировании эхо-сигнала от реального положения в ходе испытания. Это может приводить к искажению формируемого радиолокационного изображения. Вместе с тем до определенной степени отклонение может не влиять или влиять незначительно на РЛИ. При имитации крайне важно знать допустимые пределы ошибки взаимного положения носителя РСА и зондируемого участка поверхности; знать, насколько заранее рассчитанный сигнал устойчив к траекторным отклонениям. Исходя из допустимых значений ошибок легко определить границы объема пространства, при полете носителя в котором, можно использовать подготовленный заранее сигнал.
Известные из теории радиолокации подходы к оценке влияния траекторных нестабильностей [3] в данном случае не применимы. Для предлагаемого алгоритма имитации мы имеем природу образования ошибки, принципиально отличающуюся от ошибок, вызываемых траекторными нестабильностями при синтезировании апертуры. Мы абсолютно точно рассчитываем отсчеты сигнала для опорной точки. В нашем случае при неточном задании траектории ошибки проявляются и растут по мере удаления от опорной точки к краям картографируемого участка поверхности.
Поскольку расчет значений фаз и
задержек сигналов от точек РЛИ выполняется исходя из значений предполагаемой
дальности до носителя РЛС, неточность задания траектории приведет к появлению
ошибок в значениях ![]() и
и ![]() , участвующих
в (1). Это ведет к ошибкам в позиционировании эквивалентных точечных
отражателей по путевой и наклонной дальностям соответственно.
, участвующих
в (1). Это ведет к ошибкам в позиционировании эквивалентных точечных
отражателей по путевой и наклонной дальностям соответственно.
Цель работы
Определить зависимость ошибок в установке положения точечного отражателя от неточности задания траектории носителя РСА при имитации эхо-сигнала.
Постановка задачи
Будем оценивать ошибки в установке положения имитируемого отражателя по дальности и азимуту.
Рассмотрим положение носителя РЛС в некой точке траектории полета. Для режима синтезирования апертуры траектория может быть представлена дискретным набором точек (набором последовательных положений носителя в пространстве, определяемых частотой повторения зондирующих импульсов). Если для любой точки траектории отклонение носителя РСА не будет превышать допустимой величины, то влияние отклонений на всем протяжении траектории будет оставаться в допустимых пределах, определяемых условием невыхода имитируемого отражателя за границы элемента разрешения РЛС.
На рис. 1 изображена система
координат. Пусть исходный сигнал рассчитывается точно для опорного точечного
отражателя, расположенного в точке с координатами ![]() .
.

Рис. 1. Расположение носителя РСА и имитируемого отражателя.
В ходе полунатурного испытания
необходимо преобразовать этот сигнал в эхо-сигнал от отражателя, расположенного
в точке с координатами ![]() . Обозначим текущее расстояние
от РСА до точки
. Обозначим текущее расстояние
от РСА до точки ![]() как
как ![]() , а
расстояние до имитируемого точечного отражателя как
, а
расстояние до имитируемого точечного отражателя как ![]() :
:
![]() ;
;
![]()
где ![]() – координаты носителя РСА;
– координаты носителя РСА;
![]() ,
, ![]() ,
, ![]() ;
; ![]() –
сдвиг i-го отражателя по
соответствующей координатной оси относительно положения опорной точки
–
сдвиг i-го отражателя по
соответствующей координатной оси относительно положения опорной точки ![]() .
.
Формирование сигнала должно осуществляться согласно модели траекторного сигнала от точечного объекта [1]:
где ![]() – закон изменения фазы
сигнала, отражаемого точечной целью;
– закон изменения фазы
сигнала, отражаемого точечной целью; ![]() – фаза переотражения;
– фаза переотражения; ![]() – нормированная функция, характеризующая
функцию модуляции ДН реальной антенны РСА при передаче и приеме сигнала;
– нормированная функция, характеризующая
функцию модуляции ДН реальной антенны РСА при передаче и приеме сигнала; ![]() – углы визирования объекта в азимутальной
и угломестной плоскостях.
– углы визирования объекта в азимутальной
и угломестной плоскостях.
Для имитации эхо-сигнала от
отражателя, находящегося на дальности ![]() , необходимо
осуществлять коррекцию задержки сигнала на величину
, необходимо
осуществлять коррекцию задержки сигнала на величину ![]() по сравнению
с задержкой сигнала от опорной точки:
по сравнению
с задержкой сигнала от опорной точки:
где ![]() ,
, ![]() – времена задержки сигнала при
распространении до точек
– времена задержки сигнала при
распространении до точек ![]() и
и ![]() соответственно;
соответственно; ![]() – скорость распространения радиоволн.
– скорость распространения радиоволн.
Также необходимо производить изменение фазы сигнала на величину:
где ![]() ,
, ![]() – фазовые набеги при распространении сигнала
до точек
– фазовые набеги при распространении сигнала
до точек ![]() и
и ![]() соответственно;
соответственно;
![]() – волновое число;
– волновое число; ![]() – длина волны РСА.
– длина волны РСА.
Величины дополнительных задержки
![]() и фазового сдвига
и фазового сдвига ![]() определяются
разностью расстояний
определяются
разностью расстояний ![]() и
и ![]() ,
каждое из которых рассчитывается как функция от координат:
,
каждое из которых рассчитывается как функция от координат:
![]() ;
; ![]() .
.
Координаты носителя РСА ![]() , задаваемые при расчете исходного сигнала,
могут отличаться от координат определяемых условиями эксперимента:
, задаваемые при расчете исходного сигнала,
могут отличаться от координат определяемых условиями эксперимента:
![]()
где ![]() – величины отклонения
носителя по соответствующим координатам.
– величины отклонения
носителя по соответствующим координатам.
Это обстоятельство приведет к ошибке в значениях фазы и задержки имитируемого сигнала, следовательно, к отклонению имитируемого отражателя от задаваемых координат.
Смещение по дальности
Представим расстояния ![]() и
и ![]() как
функции от отклонений координат носителя
как
функции от отклонений координат носителя ![]() :
:
![]()
![]()
Тогда соответствующие отклонения расстояний:
![]() ;
;
![]() .
.
А отклонение разности расстояний будет равно:
Поскольку задержка зондирующего
сигнала однозначно связанна с расстоянием до объекта наблюдения, смещение
отметки от точечного объекта по координате дальности будет определяться
значением ![]() .
.
Проанализируем влияние
отклонений ![]() на величину
на величину ![]() . Для
этого представим каждую из функций
. Для
этого представим каждую из функций ![]() и
и ![]() в виде ряда Маклорена. Вследствие
малости, члены выше второго порядка можно не учитывать:
в виде ряда Маклорена. Вследствие
малости, члены выше второго порядка можно не учитывать:
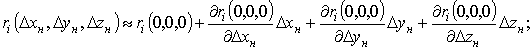
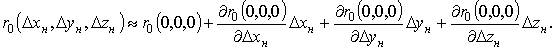
Тогда отклонения расстояний:
![]()
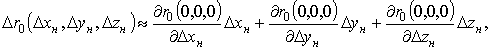
а отклонение разности расстояний:
где
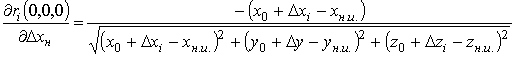 ;
; 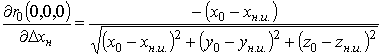 .
.
Аналогично выглядят выражения для 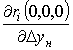 ,
, ,
,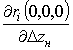 ,
, 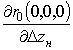 .
.
Теперь обозначим 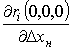 как функцию от переменных
как функцию от переменных ![]() и представим её также в виде ряда Маклорена:
и представим её также в виде ряда Маклорена:

Здесь члены второго и высших порядков
можно также опустить. Составляющая ![]() после подстановки в
(6) сократится. С учетом этого, коэффициент перед переменной
после подстановки в
(6) сократится. С учетом этого, коэффициент перед переменной ![]() в (6):
в (6):
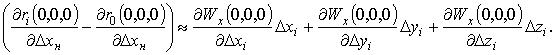
После
проведения аналогичных преобразований с коэффициентами 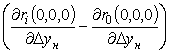 и
и
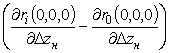 получено выражение:
получено выражение:
где ![]() .
.
Согласно (7) величина ![]() связана с величинами отклонений координат
носителя РЛС через весовые коэффициенты, значения которых зависят от положения
носителя и имитируемого точечного отражателя относительно точки
связана с величинами отклонений координат
носителя РЛС через весовые коэффициенты, значения которых зависят от положения
носителя и имитируемого точечного отражателя относительно точки ![]() :
: ![]() .
.
Смещение по азимуту
Оценим влияние неточности задания координат носителя РСА на положение по азимуту отметки от имитируемого отражателя.
Пусть РСА работает в режиме
доплеровского обужения луча (ДОЛ), угол наблюдения земной поверхности
соответствует переднебоковому обзору
(рис. 2). Носитель РЛС движется прямолинейно и равномерно. Линия пути (ЛП)
расположена параллельно оси OX,
строка РЛИ формируется вдоль ЛП. Вследствие неточности задания координат
носителя РЛС отметка от имитируемой точечной цели на РЛИ будет смещаться. Пусть
смещение происходит только по путевой дальности, в пределах одной строки РЛИ.
Рис. 2. Схема предполагаемого смещения отметки по путевой дальности.
Представим изменение во времени фазового набега сигнала (4) как соответствующее изменение доплеровской частоты сигнала. Для преобразования исходного сигнала в сигнал от имитируемого отражателя в режиме ДОЛ необходимо изменение его несущей частоты на значение разности доплеровских частот сигналов от имитируемого отражателя и опорной точки:
![]()
где ![]() ,
, ![]() – доплеровские частоты эхо-сигналов от опорной
точки и имитируемого отражателя;
– доплеровские частоты эхо-сигналов от опорной
точки и имитируемого отражателя; ![]() и
и ![]() – радиальные составляющие путевой
скорости
– радиальные составляющие путевой
скорости ![]() относительно имитируемого отражателя и опорной
точки;
относительно имитируемого отражателя и опорной
точки; ![]() – частота зондирующего сигнала.
– частота зондирующего сигнала.
Составляющие ![]() и
и ![]() представляют
собой проекции вектора скорости
представляют
собой проекции вектора скорости ![]() на направления
на направления ![]() и
и ![]() визирования
точек
визирования
точек ![]() и
и ![]() :
:
![]() ;
; ![]() ,
,
тогда
Итак, разность доплеровских
частот пропорциональна разности косинусов углов ![]() .
.
Косинусы углов наблюдения точек ![]() и
и ![]() находятся
как:
находятся
как:
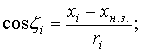
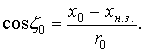
Неточность задания координат
носителя РСА приведет к отклонению значений ![]() и
и ![]() от предполагаемых при формировании
исходного сигнала.
от предполагаемых при формировании
исходного сигнала.
Обозначим
![]() и
и ![]() как
функции
как
функции ![]() и
и ![]() от
переменных
от
переменных ![]() :
:
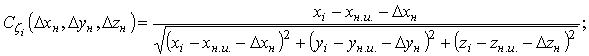
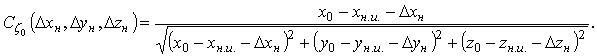
Тогда
соответствующие отклонения ![]() и
и ![]() :
:
![]()
![]()
Разность доплеровских частот при неточности задания положения носителя:
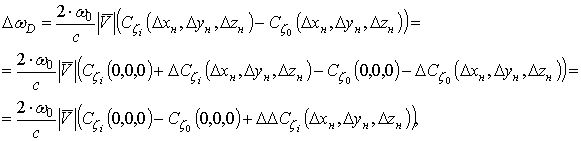
где ![]() – отклонение разности
косинусов углов наблюдения имитируемого отражателя и опорной точки.
– отклонение разности
косинусов углов наблюдения имитируемого отражателя и опорной точки.
Величина отклонения разности допплеровских частот соответственно равна:
Так как азимутальная координата
в режиме ДОЛ определяется доплеровской частотой сигнала [3], смещение имитируемого
отражателя пропорционально значению ![]() .
.
Для анализа влияния ![]() на величину
на величину ![]() достаточно
проследить их влияние на
достаточно
проследить их влияние на ![]() :
:
Аналогично операциям,
проделанным ранее для ![]() , представим каждую из функций
, представим каждую из функций ![]() и
и ![]() в
виде ряда Маклорена первого порядка:
в
виде ряда Маклорена первого порядка:
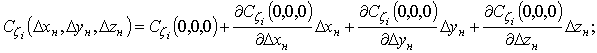
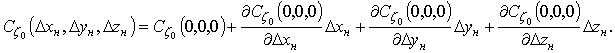
Тогда функции ![]() ,
, ![]() и
и ![]() :
:

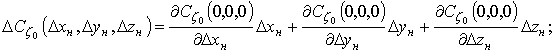
После
разложения в ряд Маклорена по переменным ![]() функций
функций
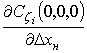 ,
,  ,
,  , выражение (11) примет вид:
, выражение (11) примет вид:
где
![]() ,
, ![]() ,
, ![]() .
.
В (12) величина ![]() связана с величинами отклонений
связана с величинами отклонений ![]() через весовые коэффициенты подобно (7)
для
через весовые коэффициенты подобно (7)
для ![]() .
.
С помощью математического моделирования проверена возможность использования (12) для режима синтезирования апертуры.
Результаты моделирования
С целью иллюстрации и проверки полученных теоретических результатов для режима синтезирования апертуры антенны проведем математическое моделирование. Рассмотрим радиолокационные изображения (рис. 3), полученные при следующих условиях:
·
Путевая
скорость носителя РЛС ![]() м/с;
м/с;
·
Частота
зондирующего сигнала ![]() ГГц;
ГГц;
·
Время
синтезирования апертуры антенны: ![]() с;
с;
·
![]() м.
м.
·
В
момент начала синтезирования ЛА находится в положении: ![]() м,
м,
![]() км,
км, ![]() .
.
В процессе синтезирования
носитель РСА осуществляет прямолинейное равномерное движение вдоль ЛП
параллельной оси X. Строка РЛИ формируется
параллельно ЛП. Считаем, что ось горизонтальной дальности параллельна оси Y
(перпендикулярна ЛП). За время синтезирования меняется относительное смещение ![]() ,
, ![]() .
.
Масштаб РЛИ составляет 1м/1пиксель. В качестве зондирующего сигнала используется простой радиоимпульс.
На РЛИ присутствуют 9 отметок
от точечных отражателей. В центре расположена отметка от опорной точки ![]() . Её положение остается неизменным, т.к.
координаты носителя для неё определены точно. Остальные 8 отметок принадлежат имитируемым
отражателям, смещенным на значения
. Её положение остается неизменным, т.к.
координаты носителя для неё определены точно. Остальные 8 отметок принадлежат имитируемым
отражателям, смещенным на значения ![]() по осям X и Y
относительно опорной точки
по осям X и Y
относительно опорной точки ![]() (рис. 3):
(рис. 3):
![]() [м].
[м].
В результате неточности задания
траектории носителя РСА их положение изменяется. Рассмотрим случай отражателя ![]() . Исходя из полученных соотношений, для него
. Исходя из полученных соотношений, для него
![]() (согласно (12));
(согласно (12)); ![]() (
(![]() Гц).
Гц).
По значению отклонения
доплеровской частоты сигнала ![]() определим смещение
отметки
определим смещение
отметки ![]() от имитируемого отражателя по азимутальной
координате на РЛИ. Рассмотрим случай работы РЛС в режиме ДОЛ. Пусть имеются два
точечных отражателя: один с координатами равными координатам имитируемого
отражателя
от имитируемого отражателя по азимутальной
координате на РЛИ. Рассмотрим случай работы РЛС в режиме ДОЛ. Пусть имеются два
точечных отражателя: один с координатами равными координатам имитируемого
отражателя ![]() ,
второй смещен относительно первого на расстояние
,
второй смещен относительно первого на расстояние ![]() по оси
X и имеет координаты
по оси
X и имеет координаты ![]() . Таким
образом, оба отражателя находятся в пределах рассматриваемой строки РЛИ
(аналогично рис. 2). Известны доплеровские смещения
. Таким
образом, оба отражателя находятся в пределах рассматриваемой строки РЛИ
(аналогично рис. 2). Известны доплеровские смещения ![]() и
и ![]() частот эхо-сигналов от отражателей и углы
их наблюдения
частот эхо-сигналов от отражателей и углы
их наблюдения ![]() и
и ![]() .
Разность доплеровских частот сигналов от отражателей:
.
Разность доплеровских частот сигналов от отражателей:
![]() .
.
Поскольку азимутальная координата в режиме ДОЛ определяется частотой сигнала и сдвиг по азимутальной оси РЛИ линейно зависит от частоты, должна быть справедлива пропорция:
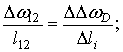
 (13)
(13)
Согласно (13) для отражателя ![]() величина смещения не должна превышать
величина смещения не должна превышать ![]() . На РЛИ максимум отметки сместился по азимутальной
координате на 3 отсчета вправо, что соответствует 3 м. Таким
образом, смешение не превышает рассчитанного значения
. На РЛИ максимум отметки сместился по азимутальной
координате на 3 отсчета вправо, что соответствует 3 м. Таким
образом, смешение не превышает рассчитанного значения ![]() .
.
Теперь рассмотрим смещение
отражателя ![]() по дальности. Исходя из (7) значение
по дальности. Исходя из (7) значение ![]() . На РЛИ максимум отметки сместился на 2
пикселя вверх (порядка 2-х метров).
. На РЛИ максимум отметки сместился на 2
пикселя вверх (порядка 2-х метров).
Рис. 3.
(а) Схема расположения имитируемых отражателей; (б) наложенные друг на друга
РЛИ: одно получено при движении носителя РСА по расчетной траектории, другое –
при движении носителя по отличной от расчетной
траектории. Вертикальная ось соответствует координате дальности (Y),
горизонтальная – азимутальной координате (X))
Видно,
что в результате неточности задания координат носителя РСА происходит переход и
«размазывание» отметок по соседним элементам разрешения. Результаты
математического моделирования соответствуют полученным теоретическим оценкам.
Согласно рассмотренному примеру, при задании координат носителя РСА с
погрешностью в 1 км отметка на РЛИ смещается на единицы метров.
Если величина смещения имитируемого отражателя не будет превышать половины элемента разрешения РСА, его отметка на РЛИ будет сохранять своё положение. Исходя из этого условия должны выбираться границы объема пространства, при нахождении носителя РСА в пределах которых можно использовать один рассчитанный заранее сигнал.
Заключение
В результате работы получены соотношения
для оценки величин отклонения разности расстояний ![]() и смещения
и смещения
![]() . Значения
. Значения ![]() и
и ![]() определяют отклонение имитируемого
точечного отражателя от задаваемых координат по наклонной и путевой дальности
соответственно.
определяют отклонение имитируемого
точечного отражателя от задаваемых координат по наклонной и путевой дальности
соответственно.
Можно сказать, что подготавливаемый заранее сигнал обладает определенной устойчивостью к неточности задания траектории носителя РСА.
Полученные соотношения позволят определить допустимые отклонения координат, задаваемых при формировании сигнала, от моделируемых координат носителя РСА. При этом ошибки по положению объектов на имитируемом РЛИ не будут превышать полученных оценок.
Таким образом, показано, что
1. Есть возможность подготовить заранее сигнал и использовать его для преобразования в РМВ при формировании имитируемого сигнала.
2. Эти результаты позволяют разбить траекторию полета носителя на N участков и рассчитать заранее N массивов отсчетов сигнала.
3. В результате, из расчетов в РМВ исключается ресурсоемкая доля вычислений (расчет законов изменения фаз и задержек парциальных сигналов в составе имитируемого эхо-сигнала, а также выполнение расчета (1)).
Литература
1. В.Н. Антипов, В.Т. Горяинов, А.Н. Кулин и др. Радиолокационные станции с цифровым синтезированием апертуры антенны/ Под ред. В.Т. Горяинова. – М.: Радио и связь, 1988 – 304 с.
2. Киселев А.В. Экономичный алгоритм имитации эхо-сигналов от распределенных пассивных помех. // Радиоэлектроника. - 1997.-N5. (Изв. высш. учеб. заведений).
3. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли/ Под ред. Г.С. Кондратенкова. – М.: «Радиотехника», 2005. – 368 с.
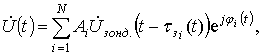
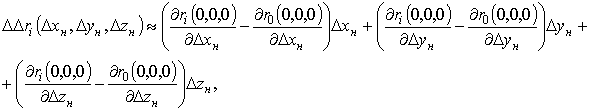



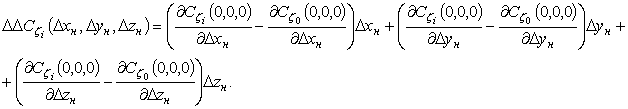
 (12)
(12) 