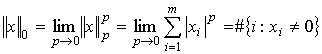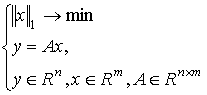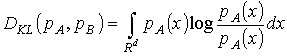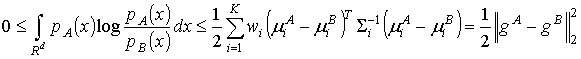МЕТОД РАЗРЕЖЕННЫХ ПРЕДСТАВЛЕНИЙ В ЗАДАЧЕ АВТОМАТИЧЕСКОЙ ТЕКСТОНЕЗАВИСИМОЙ ИДЕНТИФИКАЦИИ И ВЕРИФИКАЦИИ ДИКТОРА

 

Н. А. Любимов
 

Московский государственный университет им. М.В. Ломоносова,

факультет вычислительной математики и кибернетики

 

Получена 28 сентября 2011 г.

 

Аннотация. Задача текстонезависимой идентификации и верификации диктора (также называемая открытой задачей идентификации) является на сегодняшний день одной из наиболее важных в контексте моделирования систем распознавания человеческой речи. В данной статье описан подход, использующий метод разреженных представлений для повышения качества распознавания диктора. Эффективность предложенного подхода была продемонстрирована в рамках двух независимых экспериментов на базе фонограмм телефонного качества. Исследования показали, что применение метода разреженных представлений в открытой задаче идентификации диктора позволяет более чем в полтора раза снизить эквивалентную ошибку, повысив при этом точность идентификации.

Ключевые слова: автоматическая идентификация и верификация диктора, мел-кепстральные коэффициенты (MFCC), метод разреженных представлений, супервектор многомерных нормальных распределений, база данных телефонного качества.

Abstract. Text-independent speaker identification and verification (a.k.a. open-set speaker identification) is one of the most important problems in design of automatic speech recognition systems. This paper describes the method based on sparse representations that enhances recognition accuracy. The effectiveness of the proposed approach is demonstrated using two independent evaluations with phone-quality speech signals. It is shown that applying sparse representations in the open-set speaker identification problem reduces the equal error rate by more than half, while considerably increasing the identification rate.

Keywords: automatic speaker identification and verification, Mel-Frequency Cepstral Coefficients (MFCC), sparse representations, GMM supervector, phone-quality audio database.

 

Введение

На сегодняшний день задачи автоматической тесктонезависимой идентификации и верификации диктора (АИД и АВД) являются одними из наиболее актуальных в области компьютерной обработки речевых сигналов. Задача АИД заключается в определении идентичности диктора по фонограмме среди нескольких целевых дикторов, заявленных на поиск. В отличие от АИД, АВД ставит вопрос о принадлежности исследуемой фонограммы заявленному диктору. Комбинирование двух задач позволяет построить систему распознавания голоса, решающую открытую задачу идентификации диктора. Подобная система способна осуществлять поиск диктора по базе данных, и выдавать либо идентичность говорящего на фонограмме, либо заключение, что данный диктор в базе отсутствует.

Математические особенности решения задач АИД и АВД заключаются в том, что первая является мультиклассовой задачей идентификации, в то время как вторая задача строит бинарное решающее правило. Методы решения обеих задач используют спектральные акустические признаки речи, характеризующие голос говорящего. К наиболее часто используемым акустическим признакам можно отнести [1, 2]:

·       мел-кепстральные коэффициенты (Mel Frequency Cepstral Coefficient – MFCC),

·       перцептуальные коэффициенты линейного предсказания (Perceptual Linear Prediction – PLP),

·       кепстральные коэффициенты линейного предсказания (Linear Prediction Cepstral Coefficient – LPCC)

Каждый из этих признаков представляется вектором коэффициентов низкой  размерности (около 40 компонент), описывающим характер речевого спектра на коротком интервале времени (обычно от 20 до 50 мс). Таким образом, из каждой фонограммы достаточно большой длительности можно выделить множество таких векторов. Распределение векторов в пространстве речевых признаков моделирует индивидуальные особенности речи конкретного диктора. Одним из наиболее широко используемых подходов к моделированию распределения речевых признаков диктора является использование смеси K многомерных гауссовых функций (Gaussian Mixture Model – GMM [4]):

(1)

где   – входной вектор признаков,  – математические ожидания, ковариационные матрицы и веса компонент смеси для , а d – размерность пространства признаков.

Оценка параметров смеси называется обучением модели диктора. Эта процедура использует итерационный поиск локального максимума логарифма функции правдоподобия и называется ЕМ-алгоритмом  (Expectation-Maximization) [3]. Задача АИД состоит в оценке значений функции правдоподобия каждой обученной модели на входных векторах речевых признаков, извлеченных из тестовой фонограммы. Диктор, модель которого дает максимальное значение правдоподобия, считается искомым [4].

В АВД подход несколько сложнее. Помимо модели диктора используется так называемая универсальная фоновая модель (Universal Background Model – UBM), полученная оценкой параметров смеси гауссовых распределений на большом числе речевых данных, содержащим голоса множества дикторов. Отношение правдоподобия модели диктора к правдоподобию модели UBM задает метод проверки противоположных гипотез о принадлежности/не принадлежности тестовой фонограммы голосу анализируемого диктора [5].

Несмотря на то, что описанный подход достаточно прост и эффективен в задачах распознавания диктора, он имеет ряд существенных недостатков. Во-первых, статистический способ оценки параметров гауссовых распределений на основе EM-алгоритма предполагает наличие большого числа речевых данных целевого диктора. Во-вторых, зачастую речь, содержащаяся в фонограммах, была записана в различных условиях (например, таких как запись на микрофон, телефонный разговор, запись на диктофон на улице с шумом окружающей среды, запись в кабине самолета и пр.) В результате фонограммы одного и того же диктора могут содержать различные помехи (частотная фильтрация, нестационарный шум, реверберация и т.д.) Модели, обученные на речевых данных в одних условиях, будут давать низкие значения правдоподобия на данных того же диктора, полученных в другой акустической обстановке. Поэтому совершенствование методик АИД и АВД ведется в сторону уменьшения влияния указанных факторов, ухудшающих работу систем. В работе [6] был предложен эффективный способ решения задачи АВД на основе отображения исходных речевых признаков в пространство большей размерности. Построение модели целевого диктора в подобном пространстве эффективно даже при малом количестве речевых данных, используемых для обучения. В целом ряде работ были предложены различные способы выравнивания канала, то есть, нормализации всех различий в условиях записи фонограммы. К наиболее популярным методам канального выравнивания можно отнести:

·       Нормализация кепстрального среднего и дисперсии (Cepstral Mean Normalization – CMN, Cepstral Variance Normalization – CVM) [7]

·       Проекционный метод (Nuisance Attribute Projection – NAP) [8]

·       Совместный факторный анализ (Joint Factor Analysis – JFA) [9]

Несмотря на значительные успехи в развитии способов построения моделей дикторов и борьбе с различными канальными искажениями, в целом задачи АВД и АИД являются  не решенными на сегодняшний день и исследуются многими ведущими мировыми научными и коммерческими организациями.

Описание системы идентификации диктора

В настоящей работе предложен новый подход к решению открытой задачи идентификации, использующий концепцию разреженных представлений. Подобные подходы были рассмотрены в работах [10, 11, 17], где их эффективность была показана в задачах автоматического распознавания лиц на изображениях, а также в рамках закрытой задачи идентификации дикторов. Теория разреженных представлений (Sparse Representation) – это быстро развивающаяся область математики, находящая все больше и больше применений в различных задачах обработки и классификации сигналов [12]. Суть данной теории заключается в поиске преобразований и алгоритмов разложения, при которых исходный сигнал представим в виде малого количества ненулевых коэффициентов. Наиболее часто рассматривается следующая постановка задачи разреженного представления:

(2)

где   – исходный сигнал,  – его разреженное представление,  – матрица преобразования (называемая также словарем), такая, что .  – это псевдонорма, определяемая как предел p-нормы при :

(3)

то есть, количество ненулевых элементов в векторе . В силу того, что указанная норма не является выпуклой, стандартные алгоритмы математического программирования в чистом виде не пригодны для решения задачи (2). Множество теоретических исследований посвящено условиям применимости различных алгоритмов нахождения минимума задачи (2). Так, в работе [13] показано, что при определенных ограничениях, наложенных на матрицу , оптимальное решение задачи с нормой l₁

(4)

совпадает с глобальным минимумом решения задачи (2). Эта замена носит название релаксации исходной задачи, и позволяет применять к исходной задаче многие эффективные алгоритмы поиска глобального оптимума [14].

Для объяснения подхода к идентификации диктора, использующего принцип разреженных представлений, необходимо ввести понятие супервектора, подробно описанное в работах [6,8,11]. Пусть  – две смеси многомерных гауссовых плотностей распределения, заданных своими наборами параметров. Стандартной мерой близости двух непрерывных плотностей распределения является дивергенция Кульбака-Лейблера [8]:

(5)

 В случае если у данных плотностей распределения совпадают веса и ковариационные матрицы, причем сами матрицы имеют диагональный вид, то можно показать [8], что верхняя оценка дивергенции Кульбака-Лейблера равна:

(6)

где 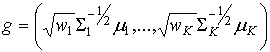 носит название супервектора многомерных нормальных распределений (GMM Supervector). Поскольку значения параметров плотности распределения речевых данных на определенном сегменте фонограммы неизвестны, используется следующая оценка для расчета значений супервекторов:

	(7)
	(8)
	(9)

  обозначает логарифм функции правдоподобия модели UBM, заданной набором параметров . Параметр  выбирается в зависимости от величины правдоподобия соответствующей компоненты в модели UBM, определяя тем самым степень смещения в направлении градиента. Поскольку математическое ожидание модели UBM не зависит от входных данных, и, следовательно, не играет роли в дальнейшей идентификации, в данной работе в формуле (7) была использована только компонента вектора-градиента, умноженного на соответствующий скаляр:

(6)

 Для каждого короткого участка фонограммы строится один супервектор размерности  Множество таких векторов, полученных из нескольких характерных высказываний диктора, образует линейное пространство, определяющее пространство речевых признаков данного диктора. Если предположить, что отличительные особенности человеческого голоса содержатся в малом количестве наблюдаемых параметров, то линейное пространство исследуемого диктора будет являться подпространством размерности . Дальнейшее предположение состоит в том, что пространства разных дикторов не пересекаются друг с другом^[1]. Это означает, что любой супервектор, рассчитанный по фонограмме диктора, должен принадлежать линейной оболочке супервекторов, полученных на обучающих фонограммах того же самого диктора:

или, другими словами, существует набор коэффициентов , одновременно не равных 0, такой что

(9)

Если теперь выделить словарь из супервекторов, рассчитанных на фонограммах N различных дикторов в виде , то получается система недоопределенных линейных уравнений  где , одним из решений которой является вектор коэффициентов _, такой что , если супервектор  принадлежит i-ому диктору. Применяя принцип разреженных представлений, легко видеть, что решение задач (2) и (4) позволяет оценить вектор , а значит, найти подпространство, отвечающее искомому диктору. Решающее правило на основе найденного решения строится следующим образом:

(10)

где   – оператор, проектирующий вектор на подпространство, отвечающее j-ому классу:

Однако на практике достаточно сложно подобрать характерные фонограммы, содержащие все уникальные речевые характеристики голоса конкретного человека. Это приводит к тому, что условие не пересечения линейных подпространств не выполняется, и пространства начинают частично перекрываться, образуя области общности голосов различных дикторов. С одной стороны, это осложняет поиск решения, так как даже нахождение глобального минимума задачи (2) вовсе не обязательно будет определять подпространство искомого диктора. С другой стороны, это позволяет классифицировать диктора как неизвестного системе, если его речевые признаки максимально разбросаны по всем подпространствам, отвечающим каждому целевому диктору. Это позволяет обойти проблему моделирования неизвестного диктора с использованием большого объема речевых данных, как это сделано в работах [5-8]. Наоборот, целевой диктор должен характеризоваться большей плотностью ненулевых коэффициентов в соответствующих индексах. Меру разброса разреженного решения задачи (4) вдоль подпространств (Sparse Concentration Index – SCI [10]) можно определить как:

(11)

Если указанная величина больше некоторого порогового значения, то входная фонограмма принимается за одного из целевых дикторов, идентичность которого находится при помощи (10). В противном случае система принимает решение о том, что диктор неизвестен, не осуществляя дальнейшего поиска. Таким образом, с использованием метода разреженных представлений одновременно решаются задачи АИД и АВД. Другим отличительным свойством предложенного подхода является отсутствие необходимости в ресурсоемком обучении модели каждого диктора (что является основой иных систем идентификации диктора, см. например [4]) – модели рассчитываются «на лету», что немаловажно при проектировании систем реального времени. Ниже представлена блок-схема работы алгоритма, решающая открытую задачу идентификации диктора:

 

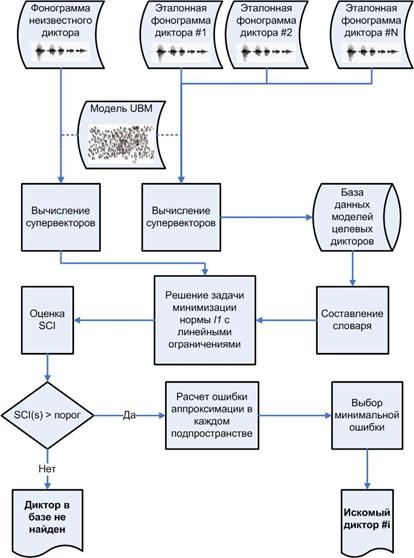
Рисунок 1. Блок-схема работы системы автоматической текстонезависимой идентификации и верификации диктора.

 

Эксперименты и результаты

Тестирование разработанной системы идентификации и верификации диктора проходило в 2 этапа. Вначале была собрана база данных русскоговорящих дикторов, содержащая фонограммы телефонного качества без значительных помех и с достаточно высоким соотношением сигнал/шум (более 15 дБ). В базе имеются записи 47 дикторов; среди них как мужские, так и женские голоса. Каждый диктор представлен эталонной фонограммой длительностью не менее 30 секунд. Запись была сделана с частотой оцифровки 8 кГц и глубиной квантования 16 бит. Общее количество тестовых записей, содержащих голоса 47 целевых дикторов, было равно 178; количество записей неизвестных системе дикторов – 173. В качестве сравнения построенная система на основе метода разреженных представлений (SRC) тестировалась совместно с общепринятым подходом к идентификации диктора на основе смеси многомерных гауссовых распределений (GMM). Речевые признаки MFCC, рассчитанные в каждом окне анализа длительностью 25 мс, были использованы в качестве входных данных для обеих систем. Для решения задачи минимизации (4) был использован итерационный алгоритм поиска знака (Feature-Sign Search - FSSA) [14]. В качестве оценок надежности работы систем были выбраны 3 характеристики, вычисляемые в процентах:

·       EER – эквивалентная ошибка ложных срабатываний/пропусков цели при верификации диктора в базе в процентах

·      IR_EER – точность идентификации (отношение правильно распознанных фонограмм к их общему количеству) диктора в случае эквивалентной ошибки

·      IR_MAX – максимальная точность идентификации (без учета ложных срабатываний), что соответствует точности идентификации при решении закрытой задачи.

Ниже приведена сравнительная таблица результатов работы системы:

 

Таблица 1. Сравнение точности работы систем идентификации на основе разреженных представлений (SRC) и на основе смеси многомерных гауссовых распределений (GMM) на базе данных русскоговорящих дикторов в телефонном качестве.

	EER, %	IREER, %	IRMAX, %
GMM	5,2	89,3	94,9
SRC	2,8	97,2	99,4

Второй эксперимент состоял в выборе базы данных реальных телефонных разговоров, разработанной в рамках международного конкурса по распознаванию диктора NIST SRE 2004 [15]. Данные выбирались из условий «8-sides», содержащих голоса большого количества дикторов (около 100), говорящих на разных языках и в разных телефонных каналах (мобильный телефон, городской телефон, беспроводной телефон), записанных различными устройствами (микрофон, телефонная трубка, гарнитура и проч.) Длительность каждой записи – примерно 5 минут. Для устранения канального искажения к речевым признакам применялись методы выравнивания посредством нормализации кепстрального среднего и дисперсии (Cepstral Mean Normalization и Cepstral Variance Normalization) [7].  Результаты сравнительной точности 2-х систем приведены ниже:

 

Таблица 2. Сравнение точности работы системы идентификации на основе разреженных представлений (SRC) и на основе смеси многомерных гауссовых распределений (GMM) на базе данных фонограмм NIST SRE 2004

	EER, %	IREER, %	IRMAX, %
GMM	24,13	71,08	81,98
SRC	18,46	79,07	86,05

Таким образом, предложенный подход позволяет существенно снизить эквивалентную ошибку системы АВД, в то время как точность идентификации остается существенно лучше по сравнению с общепринятым подходом. Проведённый анализ ошибочных срабатываний показал, что ошибки идентификации двух систем слабо коррелируют друг с другом, что открывает перспективу создания гибридной системы идентификации дикторов на основе взвешенных решений.

Выводы и дальнейшая работа

В данной работе описан подход к решению открытой задачи идентификации диктора на основе метода разреженных представлений. Несмотря на то, что теория разреженных представлений в задачах обработки и классификации сигналов уже была рассмотрена в соответствующих журналах и на конференциях [10-14,17], научная новизна данной статьи заключается в применении этой теории в контексте открытой задачи идентификации диктора в телефонном канале связи. К основным достоинствам предложенной системы можно отнести:

·       Высокую точность идентификации по сравнению с существующими системами АИД, такими как система на основе смеси многомерных гауссовых распределений;

·       Низкую ошибку ложных срабатываний;

·       Отсутствие необходимости в обучении модели диктора;

·       Гибкость калибровки за счет выбора эталонных дикторов, в пространстве которых должно быть найдено решение;

·       Небольшую вычислительную сложность (самым ресурсоемким шагом является решение задачи оптимизации (4), время выполнения которого напрямую зависит от размера словаря).

Дальнейшая работа будет заключаться в исследовании влияния выбора эталонных фонограмм на свойство полученного решения. Предполагается построить систему автоматического поиска таких наборов супервекторов, при которых области пересечения линейных подпространств каждого диктора будут минимальны. Перспективным представляется замена подхода на основе разреженного представления методом разреженных подпространств [16], в котором ищется решение с минимальным количеством ненулевых длин вектора в соответствующем подпространстве. Описанный в данной статье подход может быть применен к другим задачам обработки и классификации звуковых сигналов, таким как распознавание слитной речи и ключевых слов, сегментация аудиосигнала, разделение и локализация источников звуковых сигналов. Все эти задачи являются особо актуальными на сегодняшний день, и их решение станет важным шагом на пути к развитию систем искусственного интеллекта.

 

Литература

[1]. B. Gold, N. Morgan. Speech and Audio Signal Processing,  // John Wiley & Sons, 2000.

[2]. Аграновский А.В., Леднов Д.А. Теоретические аспекты алгоритмов обработки и классификации речевых сигналов, // - М.:  «Радио и связь», 2004. – с.    ?

[3] P. Dempster,  N. M. Laird,  D. B. Rubin “Maximum likelihood from incomplete data via the EM algorithm,”  Journal of the Royal Statistical Society, Series B, Vol. 39, No.1, pp, 1–38, 1977

[4] Douglas A.Reynolds and Richard C.Rose “Robust Text-Independent Speaker Identification Using Gaussian Mixture Speaker Models,” IEEE Transaction on Speech and Audio Processing, vol. 3, No 1, January 1995

[5] Douglas A. Reynolds, Thomas F. Quatieri, and Robert B. Dunn “Speaker Verification Using Adapted Gaussian Mixture Models,” Digital Signal Processing Vol. 10, pp. 19–41, 2000

[6] W.M. Campbell, D.E. Sturim, D.A. Reynolds, “Support Vector Machines using GMM Supervectors for speaker verification,” IEEE Signal Processing Letters, Vol. 13, Issue:5, pp. 308–311, 2006

[7] U.B. Simon, I. Lapidot, H. Guterman “Comparison between Normalizations for SVM – GMM Supervectors Speaker Verification,” IEEE 26^th Convention of Electrical and Electronics Engineers in Israel (IEEEI), 2010

[8] W.M. Campbell, D.E. Sturim, D.A. Reynolds, A. Solomonoff, “SVM Based Speaker Verification using a GMM Supervector Kernel and NAP Variability Compensation,” IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), pp. I-I, 2006

[9] Kenny, P “Joint factor analysis of speaker and session variability: Theory and algorithms,” Technical report CRIM-06/08-13  Montreal, CRIM, 2005

[10] J. Wright, A.Y. Yang, A. Ganesh, S.S. Sastry, Yi Ma “Robust Face Recognition via Sparse Representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 31, Issue 2, pp. 210–227, 2009

[11] M. Li, S. Narayanan “ Robust Talking Face Video Verification using Joint Factor Analysis and Sparse Representation on GMM Mean Shifted Supervectors,” In Proc. of IEEE int. Conf. on Audio, Speech and Signal Processing (ICASSP), 2011

[12] M. Elad, “Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing,” Springer, LLC 2010

[13] D.L. Donoho, M.Elad, “Optimally Sparse Representation in General (Non-Orthogonal) dictionaries via l₁-minimization,” Proc. of National Academy of Science (PNAS), Vol. 100, No.5, Mar. 4, 2003

[14] H. Lee, A. Battle, R. Raina, A. Y. Ng “Efficient Sparse Coding Algorithms,” Advances in neural information processing systems, Vol. 19, 2007

[15] The NIST Year 2004 Speaker Recognition Evaluation Plan, http://www.itl.nist.gov/iad/mig/tests/spk/

[16] A. Ganesh, Z. Zhou, Y. Ma, “Separation of a Subspace-Sparse Signal: Algorithms and Conditions,” Proc. of the IEEE Int. Conf. on Acoustic, Speech and Signal Processing (ICASSP), 2009

[17] I. Naseem, R. Togneri, M. Bennamoun “Sparse Representation for Speaker Identification”, 20^th  Int.Conf. on Pattern Recognition (ICPR).

 

---

[1] Это свойство более слабое, чем независимость подпространств, в котором предполагается, что размерность прямой суммы подпространств равна сумме размерностей.