УДК 621.396.67
ДВУМЕРНАЯ ДВУХПОЛЯРИЗАЦИОННАЯ ДИАГРАММОБРАЗУЮЩАЯ СХЕМА НА ОСНОВЕ СИСТЕМЫ СВЯЗАННЫХ ДВУХМОДОВЫХ МЕТАЛЛИЧЕСКИХ ВОЛНОВОДОВ
С. Е. Банков1, Г. Г. Грачев1, М. Д. Дупленкова2
1ИРЭ им. В.А. Котельникова РАН, 2ОКБ МЭИ
Получена 12 сентября 2012 г.
Аннотация. Рассматривается двумерная двухполяризационная диаграммобразующая схема на основе связанных двухмодовых металлических волноводов квадратного сечения. Диаграммобразующая схема предназначена для использования в качестве облучателя многолучевой зеркальной или линзовой антенны. В рамках приближенной теории связанных волн решена задача о возбуждении двумерной системы связанных двухмодовых волноводов собственными волнами одного из волноводов. Получено выражение для распределения амплитуд волн на выходах связанных волноводов. Обсуждается структура блока фазосдвигателей, корректирующих фазовое распределение в выходной апертуре диаграммобразующей схемы. В приближении физической оптики решена задача об излучении из диаграммобразующей схемы при возбуждении одного из ее входов. Исследуется зависимость формы диаграммы направленности излучения от параметров схемы и частоты. Показано, что анализируемое устройство может создавать систему лучей с диаграммами направленности, близкими с секторным для волн двух ортогональных линейных поляризаций.
Ключевые слова: диаграммообразующая схема, многолучевая антенна, связанные волноводы, двухмодовые металлические волноводы.
Abstract: Two-dimensional dual-polarized beam-forming network based on a system of coupled dual-mode metal waveguides of square cross section is considered. Beam-forming network may be used as a feeding device of a multi-beam mirror or lens antenna. A problem of excitation of system of coupled waveguides by eigen mode of a waveguide is solved in frame of approximate theory of coupled waves. An expression describing distribution of amplitudes of eigen modes at outputs of coupled waveguides is obtained. Structure of a block of phase shifters correcting phase distribution in output aperture of the beam-forming network is discussed. A problem of radiation from beam-forming network is solved with help of physical optics approach. Dependences of shape of radiation pattern on parameters of the network and frequency are investigated. It is shown that the analyzed device may form in free space a system of beams with sector type radiation patterns for waves with two orthogonal linear polarizations.
Keywords: beam-forming network, multi-beam antenna, coupled waveguides, dual-mode metal waveguides.
Постановка задачи
Проблема создания решеток с секторными диаграммами направленности (ДН) представляет большой интерес для теории и техники антенн различного назначения. Важнейшей частью такой решетки является диаграммообразующая схема (ДОС), которая формирует на своих выходах амплитудно – фазовое распределение (АФР), необходимое для создания секторной ДН. Одним из перспективных применений устройств данного типа является их использование в качестве облучателей оптических систем многолучевых антенн. Под оптической системой мы понимаем зеркальную или линзовую систему, формирующую излучение с игольчатой ДН.
Весьма часто многолучевая антенна должна формировать в пространстве систему лучей, пересекающихся на высоком уровне близком к – 3 дБ от максимума ДН. В такой антенне ДОС должна иметь число входов, равное числу лучей. При возбуждении ДОС со стороны любого из ее входов она формирует в пространстве излучение с парциальной секторной ДН. Фазовые центры ДН, соответствующих разным входам ДОС, смещены в пространстве. Благодаря этому смещению направление главного луча ДН, формируемой оптической системой, также смещается.
Известно, что требование к уровню пересечения лучей многолучевой антенны приводит к необходимости формировать на выходах ДОС АФР, которые также пересекаются на высоком уровне [1]. Данную задачу весьма трудно решить, если каналы ДОС изолированы и при возбуждении одного из ее входов возбуждается лишь один из элементов решетки. Поэтому распространенным подходом является создание связи между каналами ДОС, которая обеспечивает передачу энергии на группу элементов решетки от активного входа схемы.
Интересный подход к созданию ДОС предложен в работе [2], в которой для формирования АФР используется система распределенно связанных волноводов. Для создания такой ДОС хорошо подходят открытые линии передачи и волноводы с поверхностными волнами: диэлектрические волноводы, спиральные линии, полосковые и щелевые линии передачи. Различные модификации одномерных и двумерных ДОС на волноводов с распределенной связью рассмотрены в работах [3 – 5]. Отметим, что в указанных работах анализировались устройства на основе одномодовых линий передачи.
Развитием ДОС на связанных волноводах является ДОС на двухмодовых волноводах, которая потенциально может работать с волнами двух ортогональных поляризаций. В работе [6] анализируется одномерная ДОС на основе двухмодовых металлических волноводов. Показано, что такая ДОС может формировать в свободном пространстве две системы лучей с ДН, близкими по форме к секторным для волн двух ортогональных линейных поляризаций. В работе [7] решена задача о собственных волнах двумерной системы одинаковых связанных металлических волноводах. Связь между волноводами осуществлялась через систему прямоугольных отверстий в общих стенках волноводов. Данная структура анализировалась электродинамическим методом и в рамках приближенной теории связанных волн. Сопоставление двух подходов позволило построить простую модель системы связанных волноводов, позволяющую с приемлемой точностью определять ее параметры.
Данная работа является продолжением работ [6] и [7]. В ней рассматривается функционирование двумерной ДОС на основе связанных двухмодовых металлических волноводов. Кроме системы связанных волноводов, она содержит еще блок фазосдвигателей, которые корректируют фазовое распределение амплитуд волн в каналах ДОС. Решаются следующие задачи: возбуждение системы связанных волноводов конечной длины со стороны одного из ее входов и находится распределение амплитуд волн на ее выходах. Исходя из этого распределения определяется структура блока фазосдвигателей. Далее рассматривается задача излучения из ДОС. Она решается в приближении физической оптики, в рамках которого вводятся эквивалентные электрические и магнитные токи, возбуждающие свободное пространство. Поле излучения характеризуется своей ДН. Параметры ДОС выбираются таким образом, чтобы форма ДН приближалась к секторной. Особенностью данной структуры является то, что задача формирования секторной ДН ставится для двух волн с ортогональными линейными поляризациями.
1. Возбуждение системы связанных волноводов конечной длины
Схематично система связанных
волноводов, возбуждаемая со стороны одного из ее входов, показана на рис. 1.
Линиями на рис. 1 условно изображаются волноводы, оси которых параллельны оси 0z. Волноводы имеют длину ![]() .
Положение волновода в структуре описывается двумя индексами
.
Положение волновода в структуре описывается двумя индексами ![]() . Индекс
. Индекс ![]() описывает
описывает
![]() -ую координату центра волновода
-ую координату центра волновода ![]() , а индекс
, а индекс ![]() координату
по оси 0y:
координату
по оси 0y: ![]() , где
, где ![]() - период структуры. Периоды вдоль оси 0х
и 0у считаем одинаковыми.
- период структуры. Периоды вдоль оси 0х
и 0у считаем одинаковыми.
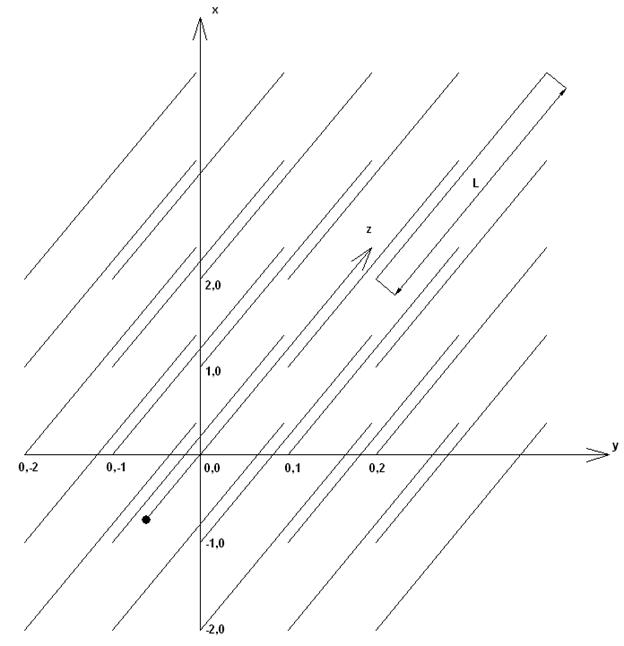
Рис. 1
В рамках описанной выше нумерации каналов возбуждение
происходит по входу с ![]() . Отметим, что мы рассматриваем
двухмодовые волноводы квадратного сечения, в которых могут распространяться две
волны, отличающиеся только плоскостью поляризации.
. Отметим, что мы рассматриваем
двухмодовые волноводы квадратного сечения, в которых могут распространяться две
волны, отличающиеся только плоскостью поляризации.
Назовем волны, у которых вектор электрического поля ориентирован вдоль оси 0х, волнами вертикальной поляризации, а ортогональные им волны волнами горизонтальной поляризации. Возбуждение системы связанных волноводов может происходить любой из указанных волн.
Распространение собственных волн в системе связанных волноводов в рамках модели, предложенной в работе [7], описывается следующей системой дифференциальных уравнений:
 (1)
(1)

где ![]() - амплитуды волн
вертикальной и горизонтальной поляризации,
- амплитуды волн
вертикальной и горизонтальной поляризации, ![]() -
линейные коэффициенты связи, которые находятся из электродинамического анализа
собственных волн структуры,
-
линейные коэффициенты связи, которые находятся из электродинамического анализа
собственных волн структуры, ![]() - постоянная
распространения собственной волны уединенного волновода,
- постоянная
распространения собственной волны уединенного волновода, ![]() - фазовые постоянные, описывающие сдвиг
фаз между полями в соседних каналах в квазипериодическом режиме. Отметим, что
поскольку мы имеем дело с квадратным волноводом, то постоянные распространения
волн ортогональных поляризаций в нем совпадают и равны
- фазовые постоянные, описывающие сдвиг
фаз между полями в соседних каналах в квазипериодическом режиме. Отметим, что
поскольку мы имеем дело с квадратным волноводом, то постоянные распространения
волн ортогональных поляризаций в нем совпадают и равны ![]() .
.
Система уравнений (1) записана для случая квазипериодического режима, в котором амплитуды волн в разных волноводах связаны следующим соотношением:
![]() . (2)
. (2)
Решения системы (1), полученные в работе [7]
имеют вид двух собственных волн, которые описываются постоянными
распространения ![]() :
:
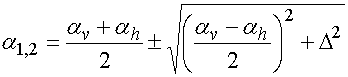 , (3)
, (3)
![]() , (4)
, (4)
![]() ,
,
![]() .
.
Отметим, что постоянные
распространения ![]() являются функциями фазовых
постоянных.
являются функциями фазовых
постоянных.
Из уравнений (1) можно получить соотношения, связывающие амплитуды вертикально и горизонтально поляризованных волн друг с другом:
![]() , (5)
, (5)
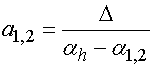
Отметим, что записанное выше
решение верно для фиксированных значений фазовых постоянных ![]() . Общее решение, описывающее амплитуды
волн в волноводах
. Общее решение, описывающее амплитуды
волн в волноводах ![]() , является суперпозицией частных
решений:
, является суперпозицией частных
решений:
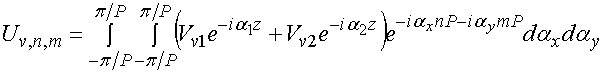 ,
,
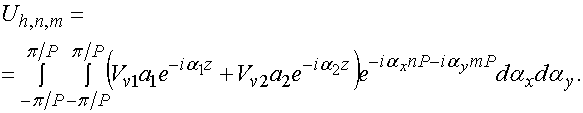 (6)
(6)
В выражениях (6) присутствуют две неизвестные
функции фазовых постоянных ![]() и
и
![]() . Для их определения
воспользуемся концевыми условиями для амплитуд волн в сечении
. Для их определения
воспользуемся концевыми условиями для амплитуд волн в сечении ![]() . Эти условия в рамках теории связанных
волн выражают требование непрерывности поля в указанном сечении. Они имеют
следующий вид:
. Эти условия в рамках теории связанных
волн выражают требование непрерывности поля в указанном сечении. Они имеют
следующий вид:
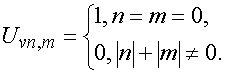 (7)
(7)
![]() .
.
Концевые условия (7) записаны для случая возбуждения структуры волной вертикальной поляризации единичной амплитуды. Случай возбуждения волной горизонтальной поляризации описывается аналогично.
Подставим соотношения (6) в условия (7) и получим следующую систему уравнений относительно неизвестных функций:
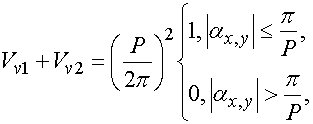 (8)
(8)
![]() .
.
Из системы уравнений (8) находим:
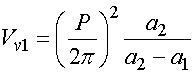 , (9)
, (9)
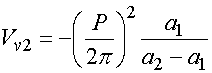 .
.
Функции ![]() отличны
от нуля в области
отличны
от нуля в области  . Подставим далее
соотношения (9) в (6) и найдем амплитуды волн на выходах системы связанных
волноводов при
. Подставим далее
соотношения (9) в (6) и найдем амплитуды волн на выходах системы связанных
волноводов при ![]() :
:

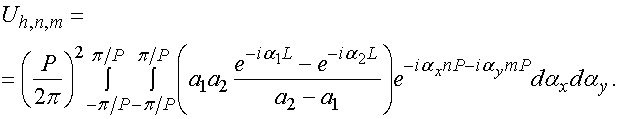 (10)
(10)
Выражения (10) решают первую часть поставленной задачи об определении амплитуд волн на выходах системы связанных волноводов. Подынтегральные функции, входящие в формулы (10), имеют весьма сложный вид. Поэтому вычисление двойных интегралов в (10) можно осуществить только численно.
2. Амплитудно-фазовое распределение в каналах ДОС на выходе блока связанных волноводов. Блок фазосдвигателей.
Рассмотрим далее распределение
комплексных амплитуд волн в каналах ДОС на выходе блока связанных волноводов.
Пример амплитудных и фазовых распределений представлен на рис. 2 – 5. Они
получены для следующих параметров структуры: размер волновода квадратного
сечения ![]() =17, период, с которым располагаются
прямоугольные отверстия связи вдоль оси 0z
=17, период, с которым располагаются
прямоугольные отверстия связи вдоль оси 0z ![]() =12, размер отверстия связи
вдоль оси 0z
=12, размер отверстия связи
вдоль оси 0z ![]() =5, размер отверстия связи в направлении,
перпендикулярном оси 0z
=5, размер отверстия связи в направлении,
перпендикулярном оси 0z ![]() =6, число периодов по оси 0z
=6, число периодов по оси 0z ![]() =17,
частота
=17,
частота ![]() =10.8 ГГц.
=10.8 ГГц.
На рис. 2 – 3 показаны
нормированные распределения модулей амплитуд волн разных поляризаций.
Нормировка происходит на модуль амплитуды волны в канале с ![]() . Отметим, что структура всегда
возбуждается по входу с
. Отметим, что структура всегда
возбуждается по входу с ![]() . Этому входу
соответствует ячейка в рис. 2 – 5, расположенная в центре. Возбуждение может
осуществляться волнами разных поляризаций.
. Этому входу
соответствует ячейка в рис. 2 – 5, расположенная в центре. Возбуждение может
осуществляться волнами разных поляризаций.
Из рис. 2 и 3, а также из рис. 4 и 5 видно, что возбуждение волнами ортогональных поляризаций порождает распределения модулей и фаз, отличающихся только поворотом на 900.
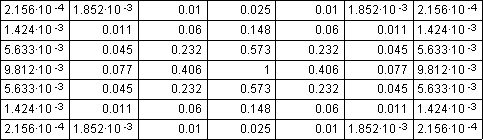
Рис. 2. Распределение модулей амплитуд волн вертикальной поляризации на выходе блока связанных волноводов при возбуждении ДОС волной вертикальной поляризации

Рис. 3. Распределение модулей амплитуд волн горизонтальной поляризации на выходе блока связанных волноводов при возбуждении ДОС волной горизонтальной поляризации

Рис. 4. Распределение модулей амплитуд волн горизонтальной поляризации на выходе блока связанных волноводов при возбуждении ДОС волной вертикальной поляризации
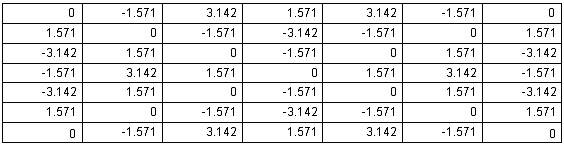
Рис. 4. Распределение фаз амплитуд волн вертикальной поляризации на выходе блока связанных волноводов при возбуждении ДОС волной вертикальной поляризации
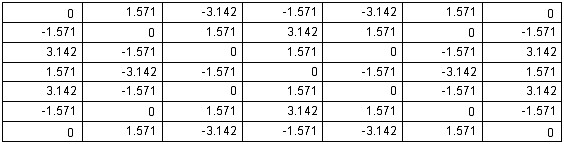
Рис. 5. Распределение фаз амплитуд волн горизонтальной поляризации на выходе блока связанных волноводов при возбуждении ДОС волной горизонтальной поляризации
Такой характер поля на выходе блока связанных волноводов обусловлен имеющейся у него симметрией поворота на 900. Поэтому в дальнейшем мы можем анализировать только случай возбуждения ДОС, например, волнами вертикальной поляризации, имея в виду, что параметры для волн горизонтальной поляризации будут идентичными в силу указанной выше симметрии структуры.
Наглядное представление о характере распределения
модулей амплитуд волн дает трехмерное распределение показанное на рис. 6. На
рис. 6 показана четвертая часть каналов ДОС. Видно, что возбуждение канала с ![]() приводит к распределению энергии между
группой соседних каналов, то есть формированию кластера. Этот эффект позволяет
в дальнейшем сформировать в свободном пространстве ДН, близкую к секторной.
приводит к распределению энергии между
группой соседних каналов, то есть формированию кластера. Этот эффект позволяет
в дальнейшем сформировать в свободном пространстве ДН, близкую к секторной.

Рис. 6. Трехмерное распределение амплитуд волн вертикальной поляризации при возбуждении ДОС волной вертикальной поляризации
На рис. 4 показано распределение модулей амплитуд
волн горизонтальной поляризации при возбуждении ДОС волной вертикальной
поляризации. Это распределение позволяет оценить эффект возбуждения кросс
поляризованных волн в ДОС. Видно, что наиболее интенсивно они возбуждаются в
каналах, расположенных на диагоналях относительно центрального канала с ![]() . При этом в каналах, расположенных на
вертикальной и горизонтальной линиях, эффект преобразования поляризации волн не
наблюдается. Можно также отметить, что амплитуды кросс поляризованных волн
существенно меньше амплитуд волн основной поляризации.
. При этом в каналах, расположенных на
вертикальной и горизонтальной линиях, эффект преобразования поляризации волн не
наблюдается. Можно также отметить, что амплитуды кросс поляризованных волн
существенно меньше амплитуд волн основной поляризации.
Важное значение для создания секторной ДН имеет
фазовое распределение. Из работ [2 – 5] известно, что создать необходимое
фазовое распределение только с помощью одинаковых связанных волноводов
невозможно. Из рис. 4 и 5 видно, что сдвиги фаз между амплитудами волн в
каналах ДОС могут быть равны ![]() , где
, где ![]() - целое число. В тоже время для создания
ДН секторного типа нам необходимо иметь синфазно - противофазное распределение,
в котором допустимы только сдвиги фаз кратные
- целое число. В тоже время для создания
ДН секторного типа нам необходимо иметь синфазно - противофазное распределение,
в котором допустимы только сдвиги фаз кратные ![]() . Для
достижения такого распределения используется блок фазосдвигателей.
. Для
достижения такого распределения используется блок фазосдвигателей.
В двухполяризационной ДОС имеется несколько вариантов построения блока фазосдвигателей. Для одномерной двухполяризационной ДОС они описаны в работе [6]. Рассмотрим далее варианты построения блока фазосдвигателей для случая двумерной двухполяризационной схемы.
Блок фазосдвигателей при возбуждении устройства
волной вертикальной поляризации можно описать с помощью коэффициентов передачи
![]() :
:
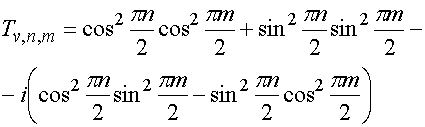 (11)
(11)
Нетрудно убедиться, что модули всех коэффициентов передачи равны единице. Их фазы в каналах показаны на рис. 7.

Рис. 7. Распределение фаз коэффициентов передачи блока фазосдвигателей для волн вертикальной поляризации
Канал с ![]() выделен
на рис. 7 цветом. Видно, что блок фазосдвигателей имеет удвоенный период по
вертикали и по горизонтали по сравнению с блоком связанных волноводов. Поэтому
соседние каналы ДОС оказываются неэквивалентными. Каналы с нулевым фазовым
сдвигом используются в качестве входов ДОС, так как только при их возбуждении
на выходе блока фазосдвигателей будет создаваться корректное синфазно –
противофазное распределение амплитуд. Оно показано на рис. 8.
выделен
на рис. 7 цветом. Видно, что блок фазосдвигателей имеет удвоенный период по
вертикали и по горизонтали по сравнению с блоком связанных волноводов. Поэтому
соседние каналы ДОС оказываются неэквивалентными. Каналы с нулевым фазовым
сдвигом используются в качестве входов ДОС, так как только при их возбуждении
на выходе блока фазосдвигателей будет создаваться корректное синфазно –
противофазное распределение амплитуд. Оно показано на рис. 8.
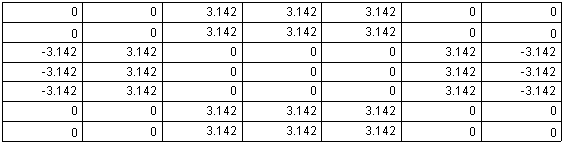
Рис. 8. Распределение фаз амплитуд вертикально поляризованных волн на выходе блока фазосдвигателей при возбуждении ДОС вертикально поляризованной волной
Из рис. 8 видно, что применение фазосдвигателей,
имеющих фазовые сдвиги (11) действительно позволяет устранить фазовые сдвиги
между амплитудами волн в каналах ДОС кратные ![]() и
получить синфазно – противофазное распределение амплитуд.
и
получить синфазно – противофазное распределение амплитуд.
Для волн горизонтальной поляризации блок
фазосдвигателей должен иметь другую структуру, если волна горизонтальной
поляризации возбуждает тот же канал с ![]() . Это
следует из того, что распределение фаз амплитуд волн горизонтальной поляризации
повернуто относительно аналогичного распределения для волн вертикальной
поляризации на 900. Поэтому, если коэффициенты передачи
фазосдвигателей для волн горизонтальной поляризации
. Это
следует из того, что распределение фаз амплитуд волн горизонтальной поляризации
повернуто относительно аналогичного распределения для волн вертикальной
поляризации на 900. Поэтому, если коэффициенты передачи
фазосдвигателей для волн горизонтальной поляризации ![]() будут
описываться выражением (11), то их использование приведет к некорректному
результату. Корректный результат дает следующее соотношение для
будут
описываться выражением (11), то их использование приведет к некорректному
результату. Корректный результат дает следующее соотношение для ![]() :
:
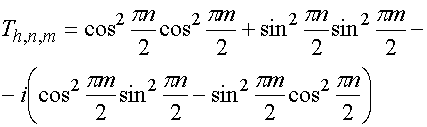 (12)
(12)
Распределение фаз коэффициентов передачи (13) отличается от распределения (11), как и следовало ожидать, только поворотом на 900. Отметим, что фазовые сдвиги, отличные от нуля в соответствии с формулами (11) и (12), возникают только в половине каналов ДОС для волн обеих поляризаций. Таким образом, в каналах, формирующих входы ДОС, фазосдвигатели отсутствуют, а в остальных каналах располагаются фазосдвигатели, имеющие разные фазовые сдвиги для волн разных поляризаций.
Возможно также размещение фазосдвигателей для
волн разных поляризаций в разных каналах. Пусть фазосдвигатели на вертикально
поляризованных волн соответствуют выражению (11). Разместим фазосдвигатели для
горизонтально поляризованных волн со сдвигом на один канал по горизонтали или
вертикали. Для этого в соотношении (12) достаточно заменить ![]() на
на ![]() или
или ![]() на
на ![]() .
Нетрудно убедиться, что в этом случае входы для волн горизонтальной поляризации
окажутся смещенными относительно входов для волн вертикальной поляризации на
один канал. Таким образом, мы получаем возможность создать ДОС, у которой волны
разных поляризаций разделяются по входам.
.
Нетрудно убедиться, что в этом случае входы для волн горизонтальной поляризации
окажутся смещенными относительно входов для волн вертикальной поляризации на
один канал. Таким образом, мы получаем возможность создать ДОС, у которой волны
разных поляризаций разделяются по входам.
3. ДН ДОС
В этом разделе мы получим выражение для ДН ДОС, возбуждаемой волной вертикальной поляризации. Как было отмечено выше, ДН волны ортогональной поляризации имеют такую же ДН, но повернутую на 900.
В качестве исходной информации
для решения поставленной задачи будем использовать распределение амплитуд волн
на выходе блока фазосдвигателей ![]() и
и ![]() , которое получается умножением амплитуд
волн на выходе блока связанных волноводов (10) на коэффициенты передачи (11) и
(12).
, которое получается умножением амплитуд
волн на выходе блока связанных волноводов (10) на коэффициенты передачи (11) и
(12).
Далее воспользуемся для определения ДН методом физической оптики. Будем описывать поле в выходной апертуре ДОС полем волноводных волн, набегающих на указанную апертуру. Введем систему координат как показано на рис. 9.
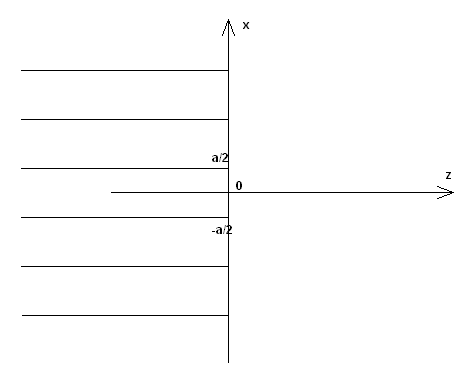
Рис. 9. Выходная апертура ДОС
ДН решетки изображенной на рис. 9 может быть записана следующим образом:
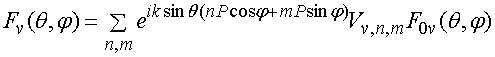 , (13)
, (13)
 ,
,
где ![]() и
и
![]() - искомые ДН для
вертикально и горизонтально поляризованных волн, а
- искомые ДН для
вертикально и горизонтально поляризованных волн, а ![]() и
и ![]() - ДН уединенного волновода для
волн соответствующих поляризаций,
- ДН уединенного волновода для
волн соответствующих поляризаций, ![]() - волновое число
свободного пространства. Сферическая система координат вводится стандартным
образом. Угол места
- волновое число
свободного пространства. Сферическая система координат вводится стандартным
образом. Угол места ![]() отсчитывается от оси 0z, а азимутальный угол
отсчитывается от оси 0z, а азимутальный угол ![]() от оси
0х. Таким образом, наша задача сводится к определению ДН уединенного волновода.
от оси
0х. Таким образом, наша задача сводится к определению ДН уединенного волновода.
Поля основных волноводных волн разной поляризации записываются следующим образом:
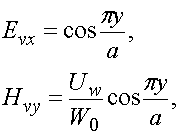 (14)
(14)
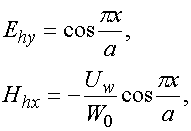
где
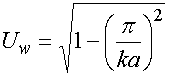 , (15)
, (15)
![]() - волновое сопротивление
свободного пространства.
- волновое сопротивление
свободного пространства.
В рамках метода физической
оптики поля в плоскости XOY заменяются эквивалентными
электрическим и магнитным токами ![]() :
:
![]() ,
,
![]() ,
, ![]() ,
, ![]() . (16)
. (16)
Для определения поля, создаваемого токами (16) в дальней зоне, воспользуемся выражением для функции Грина свободного пространства [8] и получим следующие соотношения:
 , (17)
, (17)
![]() ,
,
![]() ,
,
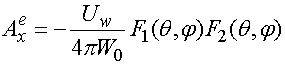 ,
,
 ,
,
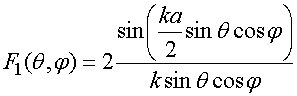 ,
,
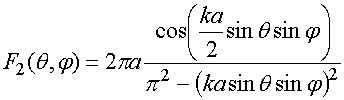 .
.
ДН ![]() связана
с ДН
связана
с ДН ![]() следующим образом:
следующим образом:
![]() .
.
На рис. 10 а-в показаны ДН, создаваемые ДОС при
возбуждении ее волной вертикальной поляризации. Кривые 1 – 3 получены для
параметров ДОС, указанных выше, и соответствуют разным значениям азимутального
угла ![]() . Отметим, что угол
. Отметим, что угол ![]() соответствует вертикальной плоскости или
плоскости вектора электрического поля, а угол
соответствует вертикальной плоскости или
плоскости вектора электрического поля, а угол ![]() соответствует
горизонтальной плоскости вектора магнитного поля. Рис. 10 а-в получены для
частот
соответствует
горизонтальной плоскости вектора магнитного поля. Рис. 10 а-в получены для
частот ![]() ГГц.
ГГц.
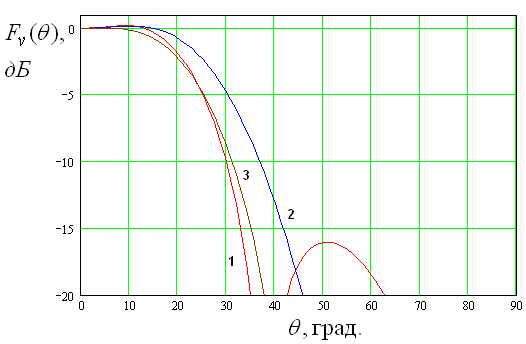
а
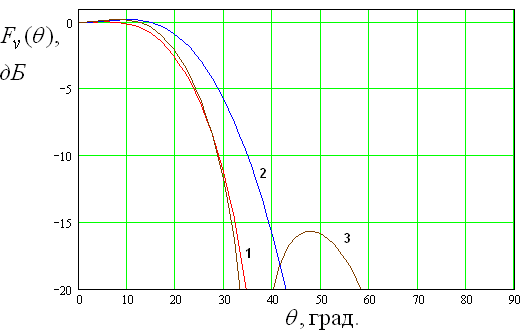
б

в
Рис. 10. ДН ДОС на частотах 11, 11.6, 12.2 ГГц
Из рис. 10 а-в видно, что ДН в главных плоскостях (вертикальной и горизонтальной) ведут себя с изменением частоты по-разному. Степень прямоугольности в вертикальной плоскости с ростом частоты уменьшается и одновременно уменьшается уровень боковых лепестков в этой плоскости. В горизонтальной плоскости, наоборот, степень прямоугольности ДН растет вместе с ростом боковых лепестков.
Обращает на себя внимание то, что на диагонали
при ![]() ДН шире, чем в главных плоскостях. Такая
ДН оптимальна для облучения оптической системы с квадратной апертурой.
ДН шире, чем в главных плоскостях. Такая
ДН оптимальна для облучения оптической системы с квадратной апертурой.
В качестве интегральной характеристики,
показывающей близость ДН к секторной, можно использовать введенный в работе [3]
коэффициент прямоугольности ![]() :
:
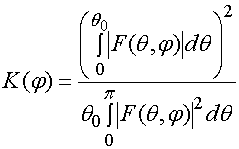 , (18)
, (18)
где ![]() - угол, определяющий
сектор, в котором ДН должна быть постоянной. За пределами этого сектора она
должна иметь нулевое значение. Из соотношения (18) видно, что в нашем
трехмерном случае, в отличие от двумерных задач, рассмотренных в работах [3 –
5], коэффициент прямоугольности зависит от угла
- угол, определяющий
сектор, в котором ДН должна быть постоянной. За пределами этого сектора она
должна иметь нулевое значение. Из соотношения (18) видно, что в нашем
трехмерном случае, в отличие от двумерных задач, рассмотренных в работах [3 –
5], коэффициент прямоугольности зависит от угла ![]() . Это
означает, что он может иметь разные значения для разных плоскостей. Аналогично
и угол
. Это
означает, что он может иметь разные значения для разных плоскостей. Аналогично
и угол ![]() также может быть функцией угла
также может быть функцией угла ![]() .
.
На рис. 11 а-б показана частотная зависимость коэффициента прямоугольности.

а
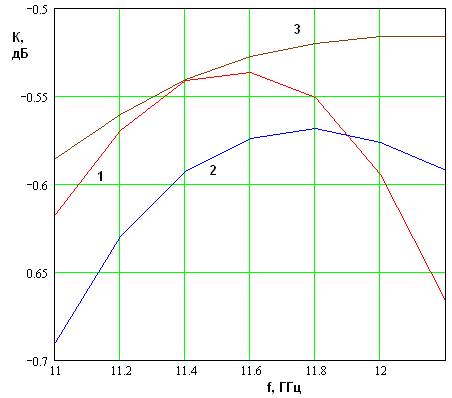
б
Рис. 11. Частотная зависимость коэффициента прямоугольности
Кривые 1 – 3 получены для ДОС с параметрами
указанными выше и соответствуют ![]() . Кривым 1 – 3
соответствуют разные значения угла
. Кривым 1 – 3
соответствуют разные значения угла ![]() . Кривые 1 и 2 получены
для
. Кривые 1 и 2 получены
для ![]() =260, а кривая 3 на рис. 11 а
для
=260, а кривая 3 на рис. 11 а
для ![]() =36.660. Такое соотношение
между углами соответствует облучению оптической системы с квадратной апертурой.
Кривая 3 на рис. 11 б получена для
=36.660. Такое соотношение
между углами соответствует облучению оптической системы с квадратной апертурой.
Кривая 3 на рис. 11 б получена для ![]() =340. Мы видим,
что коэффициент прямоугольности в диагональной плоскости увеличился при
уменьшении угла
=340. Мы видим,
что коэффициент прямоугольности в диагональной плоскости увеличился при
уменьшении угла ![]() . Отсюда можно сделать вывод,
что рассмотренная выше ДОС лучше подходит для облучения оптической системы, у
которой апертура незначительно, но отличается от квадратной формы.
. Отсюда можно сделать вывод,
что рассмотренная выше ДОС лучше подходит для облучения оптической системы, у
которой апертура незначительно, но отличается от квадратной формы.
Абсолютные значения коэффициента прямоугольности находятся в пределах 0.5 – 0.7, что несколько ниже, чем для одномерных ДОС, описанных в работах [3 – 5], но существенно лучше коэффициента прямоугольности ДН одиночного волновода, который близок к – 3 дБ.
Заключение
В работе показана возможность создания двумерной, двухполяризационной ДОС, формирующей систему лучей с ДН по форме, близкой к секторной, на основе системы квадратных металлических волноводов с распределенной связью через систему отверстий связи.
Литература
1. Вендик О.Г. Антенны с немеханическим движением луча. М.: Сов. Радио. 1965.
2. Bankov S.E., Bugrova T.I. // Microwave and Optical Technology Letters, 1993. V. 6. P. 782.
3. Банков С.Е. // Радиотехника и электроника. 2009. Т. 54. №7. С. 796.
4. Банков С.Е. // Радиотехника и электроника. 2009. Т. 54. №10. С. 1157.
5.
Банков С.Е., Калошин В.А, Фролова Е.В. // Журнал радиоэлектроники [электронный
журнал]. 2009. №3.
URL: http://jre.cplire.ru/jre/mar09/1/text.html.
6. Банков С.Е., Грачев Г.Г., Дупленкова М.Д. Одномерные двухполяризационные диаграммообразующие схемы на связанных металлических волноводах // Радиотехника и электроника. 2012. Т. 57. №6. С. 613-623.
7. Банков С.Е., Грачев Г.Г., Дупленкова М.Д. Собственные волны двумерно-периодической системы связанных двухмодовых металлических волноводов // Журнал радиоэлектроники [электронный журнал]. 2011. №11. URL: http://jre.cplire.ru/jre/nov11/13/text.html.
8. Марков Г.Т, Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Энергия, 1967.