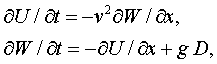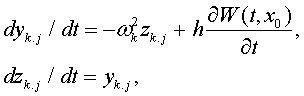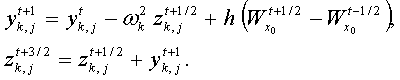УДК 534.212

Энергообмен поля и широкополосного ансамбля линейных осцилляторов, возбуждаемого коротким импульсом

 

В. Н. Корниенко ¹⁾, А. П. Привезенцев ²⁾, В. А. Черепенин ¹⁾

¹⁾ ИРЭ им. В.А.Котельникова РАН

²⁾ Челябинский государственный университет

Статья получена 3 октября  2013 г.

 

Аннотация. В работе методами вычислительного эксперимента проведено исследование динамики взаимодействия короткого импульса с ансамблем линейных осцилляторов, дискретные частоты которых равномерно распределены в спектральном диапазоне, соответствующем ширине спектра возбуждающего импульса. Показано, что в такой системе формируется периодический отклик («эхо»), и вне зависимости от наличия в ансамбле линейных осцилляторов запасенной энергии, суммарная энергия излученных импульсов отклика не превышает энергии, поглощенной ансамблем при прохождении через место его расположения исходного импульса поля.

Ключевые слова: ансамбль линейных осцилляторов, фотонное эхо.

Abstract. The dynamics of the interaction of a short pulse with an ensemble of linear oscillators, discrete frequencies which are evenly distributed in the spectral range corresponding to the width of the exciting pulse, was investigated with the methods of computational experiment. It is shown that a periodic response ("echo") is formed in such a system. Regardless of the presence of stored energy in the ensemble of oscillators, the total energy of the emitted pulse response does not exceed the energy absorbed by the ensemble as initial pulse of the field passes through its location.

Keywords: the ensemble of oscillators, photon echo.

 

 

1. Введение

Исследование отклика линейных осцилляторов с дискретным набором собственных частот на единичные импульсы внешнего воздействия было проведено в [1] в связи с выяснением возможных механизмов формирования фотонного эха [2-4]. В последнее время возросший научный интерес к подобного рода системам связан, прежде всего, с созданием искусственных сред, обладающих специфическими электромагнитными свойствами – метаматериалов [5]. Известно, что в большинстве случаев базовые элементы таких сред обладают резонансными свойствами, а значит, основные свойства среды могут быть исследованы на основе осцилляторных моделей.

В [1] было показано, что в системе «поле – линейные осцилляторы» последние излучают последовательность импульсов («эхо»), период следования которых определяется спектральным интервалом между собственными частотами осцилляторов. Однако, детального исследования генерируемой последовательности импульсов проведено не было. В частности, не был рассмотрен вопрос о динамики энергии поля и набора линейных осцилляторов.

В данной работе рассмотрены особенности самосогласованного взаимодействия ансамбля осцилляторов с частотой, изменяющейся с постоянным шагом,  с коротким биполярным импульсом волнового поля.

 

2. Постановка задачи

Рассмотрим самосогласованное взаимодействие волнового поля и ансамбля гармонических осцилляторов, который представляет собой набор  спектральных компонент с частотами , . Каждая спектральная компонента содержит  осцилляторов, в начальный момент времени равномерно распределенных по фазе колебаний. Осцилляторы расположены в области пространства, размер которой много меньше минимальной длины волны, определяемой максимальной частотой . Декремент затухания равен нулю.

В качестве модельных уравнений, описывающих состояние волнового поля, рассмотрим уравнения линии передачи, которые запишем в форме, содержащей один параметр – фазовую скорость распространения волны 

 

(1)

 

где  – напряжение,  – произведение тока на погонную индуктивность,  - суммарный дипольный момент ансамбля осцилляторов, расположенного в точке , , – погонная емкость линии, – коэффициент связи поля и ансамбля осцилляторов.

Динамику координат  и скоростей  осцилляторов описывает система связанных уравнений

 

(2)

 

Собственные частоты осцилляторов равномерно распределены в полосе частот :

.

 

В рамках этой модели проведем анализ динамики энергии поля и осцилляторов для случая, когда начальная амплитуда колебаний всех осцилляторов равна нулю, и случая с исходно запасенной в ансамбле энергией.

  

3. Численная модель

Уравнения дискретной модели взаимодействия поля и осцилляторов была получена из уравнений (1) и (2) заменой производных по времени и координате разностями на сетке с единичным шагом, аналогично работам [6,7]. Значения переменных  и  определены в узлах сетки по времени и координате. Координатные сетки для напряжения  и функции   сдвинуты на  так, что узлы напряжения  являются внутренними по отношению к узлам . Узлы временной сетки, на которых определена , сдвинуты вперед на  относительно узлов сетки для . Выбранное взаимное расположение узлов позволяет получить условно-устойчивую численную схему второго порядка [8] для решения системы (1):

 

	(3)
	(4)

 

В (3), (4) верхний индекс соответствует моменту времени, нижний – пространственной координате.

Для решения системы (2) был выбран численный метод «с перешагиванием» [9]:

 

(5)

 

Отметим, что моменты времени, в которых вычисляются отклонения осцилляторов от положения равновесия, совпадают с узлами временной сетки функции .

Если начальная амплитуда  колебаний частиц ансамбля была отлична от нуля, то осцилляторы каждой спектральной группы были равномерно распределены по фазе:

 , ,

что обеспечивало равенство нулю начального значения суммарного дипольного момента.

Исходное поле имело вид одного периода синусоиды с единичной амплитудой и пространственной длиной . Частота синусоиды  определяла полосу частот осцилляторов.

Для определения динамики энергообмена были использованы нормированные на начальную энергию импульса величины, пропорциональные энергии поля

                            

 

 

 

 

и энергии ансамбля

 

.

 

Заметим, что  вычисляется в текущий момент времени, а для получения значения  используется скользящее усреднение энергии каждого осциллятора спектральной группы по периоду колебаний .

 

4. Результаты

Моделирование динамики рассматриваемой системы проводили при следующих фиксированных значениях параметров: , , ,  . Ансамбль был расположен в точке . Расстояние между спектральными линиями ансамбля осцилляторов  было равно . Возбуждающий импульс распространялся от левого конца отрезка к правому.

На рис.1. показана зависимость поля от времени в точке с координатой  для случая, когда начальная амплитуда колебаний осцилляторов была равна нулю. Пик 1 соответствует падающему (исходному) импульсу, пик 2 – импульсу, отраженному от ансамбля, пики 3 и 4 – импульсам периодической последовательности («эха»).

 

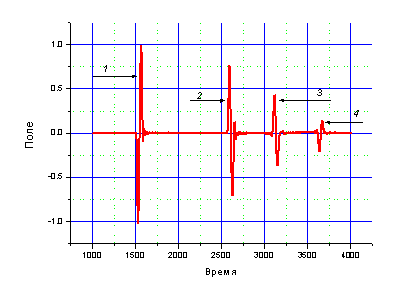
Рис.1. Зависимость поля от времени в фиксированной точке наблюдения.

 

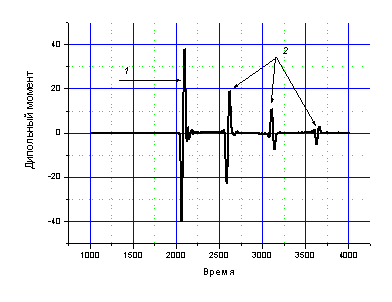
Рис.2. Зависимость суммарного дипольного момента от времени.

 

На рис.2. приведена временная зависимость суммарного дипольного момента ансамбля. Формирование пика 1 происходит в момент частичного поглощения ансамблем энергии падающего импульса поля. В этот же момент в точке расположения ансамбля формируется отраженный импульс поля. Периодическое совпадение фаз колебаний осцилляторов, имеющих различные собственные частоты, приводит к возникновению пиков 2, которые и обеспечивают отклик ансамбля в виде «эха». Амплитуда пиков 2 с течением времени уменьшается.

 

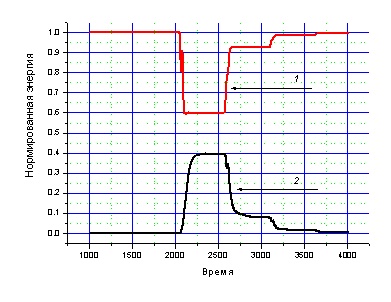
Рис.3. Зависимость энергии поля и ансамбля от времени при нулевой начальной амплитуде колебаний осцилляторов.

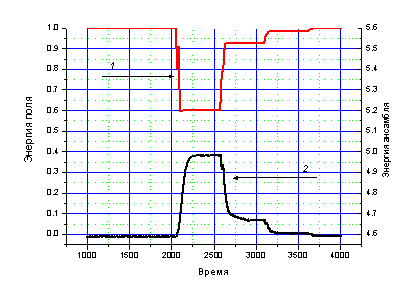
Рис.4. Зависимость энергии поля и ансамбля от времени при начальной амплитуде колебаний осцилляторов, равной 1.5 (отн. ед.).

 

На рис.3. показано изменение энергии поля (кривая 1) и ансамбля осцилляторов (кривая 2) со временем. В момент прохождения импульса через ансамбль происходит его частичное поглощение (первая ступенька кривых 1,2). Последующее формирование импульсов «эха» приводит к потере ансамблем энергии и, соответственно, увеличению энергии поля. Отметим, что конечное и начальное значения энергии поля и соответствующие значения энергии ансамбля частиц совпадают.

Такое же поведение энергии сохраняется и при ненулевых значениях амплитуд колебаний осцилляторов (рис.4.). Т.е. суммарное количество отдаваемой ансамблем полю энергии всегда не больше поглощенной им энергии.

 

5. Выводы

Результаты проведенных вычислительных экспериментов показывают, что в системе «поле – ансамбль линейных осцилляторов с дискретным набором собственных частот» формируется последовательность импульсов отклика, период следования которых соответствует обратной величине спектрального интервала между собственными частотами осцилляторов ансамбля. Амплитуда импульсов последовательности с течением времени уменьшается. Изменение энергии ансамбля  и поля во времени имеет ступенчатый характер, временное положение каждой «ступеньки» соответствует локальному максимуму суммарного дипольного момента осцилляторов. Вне зависимости от наличия в ансамбле линейных осцилляторов запасенной энергии, суммарная энергия излученных импульсов отклика не превышает энергии, поглощенной ансамблем при прохождении через место его расположения исходного импульса поля.

 

Литература

1. Б.Я.Дубецкий, В.П.Чеботаев // Письма в ЖЭТФ. 1985. Т.41. Вып.6. С.267.

2. Аллен Л., Эберли Дж. Оптический резонанс и двухуровневые атомы. М.: 1978.

3. Шумейкер Р. Когерентная инфракрасная спектроскопия нестационарных процессов. В кн. «Лазерная и когерентная спектроскопия», М.: 1982.

4. V.P. Chebotayev and B.Ya.Dubetsky // Appl.Phys. B 31, 45-52 (1983).

5. В.М.Агранович, Ю.Н.Гартштейн // Усп.физ.наук. 2006. Т.176. №10. С.1051.

6. В.Н.Корниенко, А.П.Привезенцев // РиЭ. 2012. Т.57. №2. С.211.

7. В.Н.Корниенко, А.П.Привезенцев // РиЭ. 2013. Т.58. № 7. С. 691.

8. Allen Taflove. Computational Electrodynamics: the finite-difference time-domain method. Artech Hous. Boston-London. 1995.

9. Р.Хокни, Дж.Иствуд. Численное моделирование методом частиц. М., «Мир»: 1987.