УДК 621.373.121.1
Прецизионное термостатирование резонатора на объёмных акустических волнах. Моделирование и синтез системы управления
А. П. Загороднов, А. Н. Якунин
Институт проблем точной механики и управления РАН, г. Саратов
Статья получена 25 октября 2013 г.
Аннотация. В работе приведены результаты поиска решения актуальной проблемы прецизионного термостатирования сапфирового резонатора на объёмных акустических волнах – на уровне не хуже 3,3·10-6°С. Обоснована необходимость построения системы термостабилизации на основе двух последовательно соединенных термоэлектрических модулей с введением демпфирующего слоя между ними. Предложена система управления, синтезированная с учетом динамических свойств такой структуры, описан алгоритм её настройки, исследованы особенности переходных процессов. Приведены результаты моделирования системы термостабилизации, доказывающие принципиальную возможность построения генератора на сапфировом резонаторе на объёмных акустических волнах для современных систем радиолокации с повышенной чувствительностью и разрешением.
Ключевые слова: радиолокация, резонатор на объёмных акустических волнах, прецизионная термостабилизация, моделирование, система управления.
Abstract: The results of the solutions of actual problem - the precision (at a level not less then 3,3·10-6°С) temperature control of a sapphire high-overtone bulk-acoustic resonator are presented in the paper. Necessity of thermal stabilization of system construction based on two thermoelectric modules connected in series with introduction of a damping layer between them is justified. A control system has been synthesized taking into account the dynamic properties of such a structure, an algorithm of its configuration is described, features of transients are investigated. The results of simulation of thermal stabilization system, proving the fundamental possibility of creation of a generator on a sapphire high-overtone bulk-acoustic resonator for modern radar systems with high sensitivity and resolution, are presented.
Keywords: radiolocation, high-overtone bulk-acoustic resonator, precision thermostatting, simulation, control system.
Введение
Построение высокочастотных генераторов с использованием миниатюрных высокодобротных сапфировых резонаторов на объёмных акустических волнах (ОАВ) является перспективным направлением снижения уровня фазовых шумов генераторов [1], повышения чувствительности и разрешающей способности современных систем радиолокации. Однако электрофизические свойства сапфира определяют существование высокого температурного коэффициента частоты резонатора [2], вследствие чего разработка высокостабильного генератора на основе ОАВ делает обязательным и принципиально важным этап создания системы прецизионного термостатирования резонатора. Так, генератор с рабочей частотой 1 ГГц и точностью установки частоты 0,1 Гц (относительное отклонение частоты составляет 10-10 и является типичным для систем радиолокации с активной фазированной антенной решёткой) требует поддержания температуры резонатора с точностью не хуже 3,3·10-6°С [3].
Как показывает анализ существующих средств прецизионного термостатирования, наибольшей точностью поддержания температуры на уровне 5·10-3°С обладают приборы компании ООО «ИзТех» [4]. При этом такие термостаты имеют значительные габаритные размеры (не менее 30 см в каждой проекции).
Поэтому постановка и решение задачи поиска технического решения для создания миниатюрной системы прецизионного термостатирования резонатора на ОАВ, обеспечивающей отклонение частоты менее 10-10 от номинала, является актуальной.
1. Выбор схемы построения системы термостабилизации
Выбор схемы построения системы термостабилизации удобно осуществлять методом экспресс-анализа динамических характеристик систем прецизионного термостатирования. В соответствии с данным методом используется упрощённая модель без учёта управляющего контура, что позволяет определить принципиальную возможность применимости исследуемой конструкции системы термостабилизации для обеспечения требуемых параметров. Предлагаемый метод [5] включает три этапа. На первом этапе производится расчёт стационарного режима работы термостата, на втором – определяются теплоинерционные свойства системы, на третьем – даётся оценка времени компенсации отклонения температуры.
На этапе «Расчёт стационарного режима» производится анализ стационарных режимов работы системы, определяются номинальные температура и управляющее воздействие, а также рабочий диапазон управляющего воздействия.
На этапе «Определение теплоинерционных свойств» рассчитываются максимально возможная скорость изменения температуры стабилизируемого объекта при изменении температуры окружающей среды, а также максимально возможное отклонение температуры за время, необходимое для измерения температуры.
На этапе «Оценка времени компенсации отклонений температуры» определяется влияние конструктивно-технологических факторов системы термостатирования на время компенсации отклонений.
При исследовании известных схем построения системы термостабилизации, а именно, – схемы на основе нагревательного элемента и схемы на основе термоэлектрического модуля (ТЭМ) – выявлено, что они не позволяют в силу присущих им конструктивных ограничений поддерживать температуру с требуемой точностью [5]. Так, система термостатирования на основе нагревательного элемента способна поддерживать температуру с предельной точностью до 6,2·10-4°С, что соответствует отклонению частоты на 19 Гц. Система термостатирования на основе ТЭМ способна поддерживать температуру с предельной точностью до 1,7·10-4°С, что соответствует отклонению частоты на 5 Гц. Таким образом, стабильность данных систем на 1-2 порядка ниже требуемой.
Существенного улучшения параметров термостабилизации можно достичь при применении предложенной в [5] двухконтурной системы термостатирования, имеющей два последовательно соединенных ТЭМ с демпфирующим слоем между ними, как показано на рис. 1.

Рис. 1. Двухконтурная система
термостатирования с демпфирующим слоем
(1 – резонатор в корпусе; 2 – внешний корпус; 3 – принудительное воздушное охлаждение; 4 – демпфирующий слой; 5 – ТЭМ)
Результаты моделирования системы термостабилизации, проведенного в [5], доказали потенциальную способность такой схемы обеспечить стабилизацию температуры резонатора с точностью до 2·10-6°С, что соответствует отклонению частоты на 0,06 Гц. Улучшение показателей достигается благодаря увеличению теплового сопротивления (использование двух последовательно установленных ТЭМ вместо одного) и тепловой инерционности (введение промежуточного демпфирующего слоя). Важным конструктивным элементом системы на рис. 1 является демпфирующий слой, который позволяет значительно снизить скорость изменения температуры резонатора при колебаниях температуры окружающей среды. Этого невозможно добиться при использовании стандартных выпускаемых блоков, состоящих из двух последовательно соединённых ТЭМ.
Приведённые выше результаты получены без учёта системы управления и определяются исключительно конструктивными особенностями термостата. Поскольку применение системы управления может внести некоторые коррективы в определение уровня погрешности, то следующие разделы настоящей работы посвящены разработке методики синтеза и моделированию системы прецизионного термостатирования с учетом функционирования всех компонентов управляющей системы.
2. Методика синтеза системы управления термостабилизацией
Рассмотрим двухконтурную систему термостатирования с демпфирующим слоем (рис. 1).
Резонатор 1 в данной конструкции связан через сопряжённый с ним ТЭМ (первый ТЭМ) с демпфирующим слоем 4, а связь с окружающей средой осуществляется через демпфирующий слой. Это позволяет упростить методику моделирования системы управления термостата в целом.
Температура демпфирующего слоя 4 зависит от температур резонатора 1 и внешней среды. Однако влияние температуры резонатора 1 и воздействие сопряженного с ним первого ТЭМ много меньше влияния температуры окружающей среды и воздействия ТЭМ (второй ТЭМ), сопряженного с корпусом 2. Такое соотношение обусловлено меньшими уровнями рассеиваемой в резонаторе мощности задающего сигнала и мощности первого ТЭМ по сравнению с мощностью второго ТЭМ и теплового потока через корпус, возникающего при любом изменении температуры окружающей среды.
Перечисленные особенности (разномасштабность по тепловой инерции и тепловым потокам) позволяют рассматривать системы управления первым и вторым ТЭМ как автономные. При этом сначала должна быть настроена система управления вторым ТЭМ, а затем произведена настройка системы управления первым ТЭМ при системе управления вторым ТЭМ, находящейся в рабочем режиме.
Построение системы управления как первого, так и второго ТЭМ осуществляется в соответствии с единым алгоритмом. При обнаружении отклонения температуры от номинальной [3] в системе управления генерируется команда на осуществление кратковременного воздействия (компенсирующий импульс с длительностью действия, равному периоду регистрации сигнала отклонения, что в рассматриваемой системе составляет 1 мс) с целью компенсации накопленного отклонения температуры. Уровень воздействия близок к уровню, определяемому пропорциональным звеном ПИД-регулятора, поэтому далее будет обозначаться как пропорциональный компонент. Вместе с компенсирующим импульсом в системе регулируется величина постоянного управляющего воздействия для поддержания объекта управления в требуемом диапазоне температур. Данное действие близко к интегральному звену ПИД-регулятора, поэтому далее будет обозначаться как интегральный компонент.
Использовать классический ПИД-регулятор [6] в данной системе управления не представляется возможным, так как в ней отсутствуют периодические данные об отклонении температуры, а состояние системы известно только в моменты обнаружения отклонения частоты от ожидаемого. Однако основные параметры такой системы близки к параметрам ПИД-регулятора, что позволяет использовать алгоритм экспериментальной настройки пропорционального и интегрального компонентов, близкий к описанному в [7] алгоритму настройки ПИД-регулятора.
При настройке системы управления внешнее воздействие задаётся в виде скачкообразного изменения температуры окружающей среды на величину, соответствующему максимально допустимому отклонению (в нашем 1°С). Данный вид воздействия позволяет получить оценку сверху, так как моделирует более жёсткий режим по сравнению с реальным [8].
После завершения настройки системы управления в жестком режиме проводится ее тестирование на линейное и синусоидальное изменения температуры.
3. Настройка системы управления вторым ТЭМ
Сначала производится подбор пропорционального компонента Kp2 системы. Анализ производится на небольшом промежутке времени t (50 с), так как в силу особенностей конструкции [3] в данной системе регистрируются лишь сравнительно малые (порядка 1 кГц) отклонения частоты, а значит и температуры, возникающие при отсутствии интегрального компонента.
При увеличении пропорционального компонента наблюдается увеличение разности отклонения температуры объекта DTD в момент обнаружения отклонения температуры (кривая 1 рис.2а, 2б и 2в) и после компенсирующего импульса (кривая 2 рис.2а, 2б и 2в).

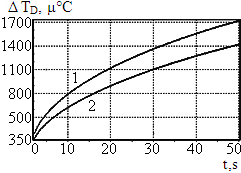
а) Kp2 = 1 б) Kp2 = 4
в) Kp2 = 16 г) Kp2 = 32
Рис. 2. К
настройке пропорционального компонента Kp2
При достижении определённого значения разность практически перестаёт изменяться (кривые 1 и 2 рис. 2в и 2г), так как холодопроизводительность ТЭМ является нелинейной функцией и имеет ограничение, то дальнейшее увеличение пропорционального компонента выше некоторого уровня не приводит к увеличению компенсирующего импульса.
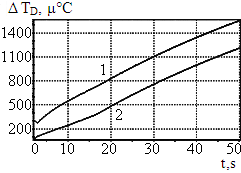
Далее производится настройка интегрального компонента Ki2. При его возрастании уменьшается отклонение температуры объекта DTD на протяжении рассматриваемого интервала времени как во время обнаружения (кривая 1 рис. 3а, 3б, 3в, 3г), так и после кратковременного воздействия (кривая 2 рис. 3а, 3б, 3в, 3г).
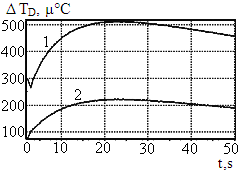
а) Ki2 = 1 б) Ki2 = 4

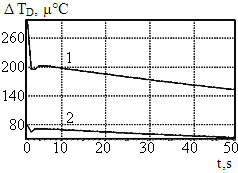
в) Ki2 = 16 г) Ki2 = 40
Рис. 3. К
настройке интегрального компонента Ki2
Из приведённых на рис. 3 данных видно, что увеличение Ki2 приводит к уменьшению как времени стабилизации (точка наибольшего по величине регистрируемого отклонения температуры смещается влево по оси времени), так и уровня отклонения температуры. Вместе с тем необходимо обращать внимание на то, что чрезмерное повышение интегрального компонента приводит к увеличению амплитуды автоколебаний при выходе системы в стационарный режим (см. рис. 4а и 4б).
Рекомендуется выбирать такой уровень интегрального компонента, при котором уровень отклонения температуры во всем рассматриваемом диапазоне времени не превосходит первое обнаруженное отклонение температуры. При этом необходимо учитывать, что подбором компонентов системы управления добиться уменьшения значения первого обнаруженного отклонения невозможно.
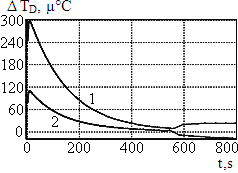

а) Ki2 = 16 б) Ki2 = 40
Рис. 4.
Автоколебания температуры демпфера в стационарном режиме
4. Настройка системы управления первым ТЭМ
Аналогично рассмотренному выше этап настройки системы управления первым ТЭМ начинается с подбора пропорционального компонента Kp1.
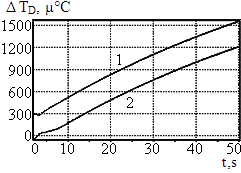
При увеличении пропорционально компонента наблюдается приближение кривой колебания отклонения температуры резонатора DTР к нулю (см. рис. 5а, 5б, 5в).
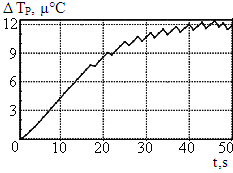

а) Kp1 = 1 б) Kp1 = 4
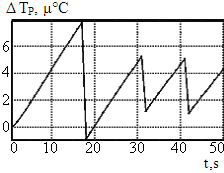
в) Kp1 = 16
Рис. 5. К настройке пропорционального компонента Kp1
Рекомендуется выбирать такой коэффициент Kp1, при котором наблюдается лишь незначительное перерегулирование (переход через ноль), как показано на рис. 5в, и учитывать, что дальнейшее увеличение пропорционального компонента приведёт к дестабилизации системы.
Затем производится настройка интегрального компонента Ki1. При настройке данного компонента необходимо значительно увеличивать исследуемый интервал времени t (до 800 с), так как время переходных процессов и время установления квазистационарного режима растут, и малые временные интервалы не являются показательными для настройки.
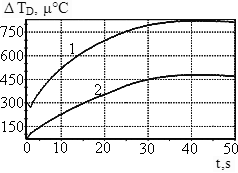
С ростом Ki1 увеличивается скорость затухания колебаний отклонения температуры резонатора DTР (см. рис. 6а, 6б). Однако рекомендуется выбирать такой коэффициент Ki1, при котором наблюдается незначительное перерегулирование (переход через 3·10-6°С на рис. 6б). При дальнейшем увеличении интегрального компонента возможны кратковременные выходы системы за требуемый температурный диапазон.

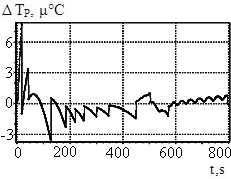
а) Ki1 = 1 б) Ki1 = 8
Рис. 6. К
настройке интегрального компонента Ki1
Данный алгоритм настройки системы управления прецизионной термостабилизацией является общим и может быть адаптирован при предъявлении каких-либо специфических требований к системе.
5. Моделирование функционирования системы термостабилизации
Функционирование полностью настроенной системы управления анализируется при воздействиях, приближенных к реальным в условиях использования кондиционированного воздуха для обдува внешнего корпуса. При этом отклонение температуры воздуха от номинала не превышает 1°С. Кроме того, учитывается дискретизация управляющего воздействия и задержка управляющего воздействия от момента обнаружения отклонения температуры, обусловленных использованием цифровых элементов.
Проведено исследование влияния линейно изменяющейся во времени температуры окружающей среды (1°С за время 300 с, далее температура не меняется). Этот вид воздействия более мягкий, чем скачкообразное изменение температуры. Результаты на рис. 7а показывают, что предлагаемая система при данном виде воздействия удерживает резонатор в заданном диапазоне температур. Так, на участке линейного изменения температуры окружающей среды отклонение температуры резонатора не превышает 3·10-6°С. Далее отклонение температуры резонатора колеблется в диапазоне ±2·10-6°С. При этом приблизительно через время равное 700 с система входит в стационарный режим с автоколебаниями. Скачкообразное изменение температуры резонатора в режиме автоколебаний обусловлено срабатываем внутреннего контура системы термостабилизации, плавное изменение — работой внешнего контура.
Синусоидальное изменение температуры окружающей среды с амплитудой 1°С и периодом колебаний 200 с является более жёстким по сравнению с предыдущим рассмотренным вариантом. Результаты моделирования, приведённые на рис. 7б, показывают, что при данном виде воздействия резонатор также удерживается в заданном диапазоне температур. Скачкообразное изменение температуры резонатора, как и в случае автоколебаний в стационарном режиме, обусловлено срабатываем внутреннего контура системы термостабилизации, плавное изменение — работой внешнего контура. При этом колебания отклонения температуры резонатора не превышают 1,5·10-6°С. Таких результатов удаётся добиться благодаря демпфирующему слою, сглаживающему периодическое внешнее воздействие.
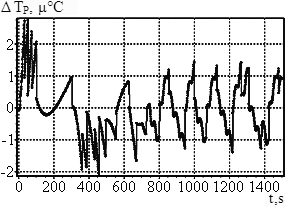
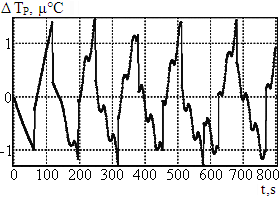
а) Линейное б) Синусоидальное
Рис.7. Функционирование системы термостабилизации при различных видах изменения температуры окружающей среды
Моделирование функционирования системы термостабилизации при линейном и синусоидальном изменении температуры окружающей среды показывает способность предлагаемой системы удерживать температуру резонатора в требуемых пределах и пригодность предлагаемой системы к использованию.
Заключение
В настоящей работе найдено и описано решение актуальной проблемы создания системы термостабилизации сапфирового резонатора на объёмных акустических волнах, заключающейся в необходимости поддержания температуры с прецизионной точностью – в единицы микроградусов. Показано, что требуемую точность поддержания температуры можно обеспечить лишь применением конструкции системы термостабилизации на основе двух последовательно соединенных термоэлектрических модулей с введением демпфирующего слоя между ними. Такая конструкция позволяет уменьшить влияние изменений температуры окружающей среды на два порядка по сравнению с традиционной схемой на основе одного термоэлектрического модуля. Предложена двухуровневая система управления термостабилизации, адаптирующая классическую систему ПИ-регулятора к нетрадиционным условиям – отсутствию периодических данных об ошибке. Представлен алгоритм настройки системы управления, аналогичный алгоритму экспериментальной настройки классического ПИД-регулятотра. Приведены результаты моделирования предложенной системы термостабилизации, доказывающие принципиальную возможность построения генератора на сапфировом резонаторе на объёмных акустических волнах для современных систем радиолокации с повышенной чувствительностью и разрешением.
Литература
1. Балышева О. Л., Григорьевский В. И., Гуляев Ю. В. и др. Акустоэлектронные устройства обработки и генерации сигналов. Принципы работы, расчёта и проектирования: монография под ред. Гуляева Ю. В. М.: Радиотехника, 2012. 412 с.
2. Driscoll M.M et al. Extremely low phase noise UHF oscillators utilizing high-overtone, bulk-acoustic resonators. IEEE Trans. Ultrason., Feroelec., Frec. Contr. November 1992. Vol. 39. No. 6. P. 774-779.
3. Загороднов А. П., Якунин А. Н. Вопросы построения малошумящего высокочастотного опорного генератора //Научное приборостроение. 2012. Т22. №1. С. 19-24.
4. Прецизионные измерители температуры // Каталог продукции ООО «Изтех». Зеленоград, 2012. [Электронный ресурс]. URL: http://www.iztech.ru (дата обращения: 24.10.13).
5. Загороднов А. П., Якунин А. Н. Исследование динамических свойств систем прецизионной термостабилизации резонатора. Материалы 10-й юбилейной Международной научно-технической конференции «АПЭП-2012», 19-20 сентября 2012. С. 162-163.
6. Справочник по теории автоматического управления / Под ред. Красовского. А.А. М.: Наука. Гл. ред. физ.-мат. лит., 1987. 712 с.
7. Wescott T. Applied Control Theory for Embedded Systems. Newnes: Elsevier, 2006. 320 p.
8. Методы классической и современной теории автоматического управления: Учебник в 5-и тт.; 2-е изд., перераб. и доп. Т. 1: Математические модели, динамические характеристики и анализ систем автоматического управления / Под ред. К. А. Пупкова, Н. Д. Егупова. М.: Издательство МГТУ им. Н. Э. Баумана, 2004. 656 с.