УДК 621.391
МЕТОДЫ И АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ ВЕТРОВОГО КОГЕРЕНТНОГО ДОПЛЕРОВСКОГО ЛИДАРНОГО ПРОФИЛОМЕТРА С КОНИЧЕСКИМ СКАНИРОВАНИЕМ
В. Р. Ахметьянов, Д. Н. Васильев, М. А. Коняев, О. А. Мишина, М. С. Пенкин, Г. А. Петров, Я. А. Тезадов, И. В. Шаталов, И. Ф. Ширяев
ООО “НПП “Лазерные системы”
Статья получена 4 сентября 2013 г., после доработки – 28 октября 2013 г.
Аннотация. В работе рассмотрены вопросы, связанные с программно-алгоритмическим обеспечением ветрового когерентного доплеровского лидарного профилометра, предназначенного для оперативного мониторинга ветровых характеристик атмосферы и, в частности, для определения такого метеоявления, как сдвиг ветра в районе взлетно-посадочной полосы аэропорта. Описан принцип работы лидарного профилометра с непрерывным коническим сканированием. Приведены методы и алгоритмы обработки лидарного сигнала, составляющие основу программно-алгоритмического обеспечения профилометра.
Ключевые слова: скорость и направление ветра, доплеровский лидар, методы и алгоритмы обработки сигнала.
Abstract: The paper deals with questions related to the program-algorithmic software of the wind coherent doppler lidar profiler, which is intended for operational monitoring of the wind characteristics of the atmosphere and, in particular, to determine such meteorological phenomenon as wind shear in the area of the airport's runway. The principle of operation of the lidar profiler with continuous conical scanning is described. Methods and algorithms of processing of lidar signal, as the basis of the profiler program-algorithmic support, are considered.
Key words: wind speed and direction, doppler lidar, methods and algorithms for signal processing.
1. Введение
В самых различных сферах жизнедеятельности человека требуется информация о ветровых характеристиках атмосферы. В результате в настоящее время для определения таких параметров ветра, как его скорость и направление, все более широкое распространение получают дистанционные методы зондирования атмосферы. Благодаря развитию технологической базы и бурному росту вычислительных мощностей компьютерной техники активно развиваются лидарные методы, в основе работы которых лежит эффект Доплера. В соответствии с достигнутым техническим уровнем в нормативных документах ICAO [1] в настоящее время рекомендуется внедрение ветровых когерентных доплеровских лидаров (КДЛ) в систему метеорологического обеспечения авиационной безопасности [2].
Работа КДЛ построена на допущении, что лазерное излучение на частоте f по мере распространения в атмосфере рассеивается на аэрозольных частицах. С учетом скорости движения этих частиц частота обратно рассеянной волны изменяется согласно эффекту Доплера.
В рассматриваемом типе когерентных доплеровских ладарах приемник рассеянного аэрозольными частицами сигнала расположен в том же месте, где и передатчик. Следовательно, выражение для частотного сдвига может быть записано следующим образом:
,
где Vr – радиальная составляющая скорости ветра или иначе проекция мгновенного вектора скорости V={Vx, Vy, Vz} на направление зондирования. Таким образом
,
где 
– непосредственно измеряемый
доплеровский сдвиг частоты.
Необходимо отметить, что в существующих и разрабатываемых КДЛ может использоваться как импульсное, так и непрерывное лазерное излучение. КДЛ с импульсным излучением, как правило, позволяет проводить зондирование атмосферы на расстояние от сотни метров до десятков километров. В то же время для обеспечения мер авиационной безопасности в приземном слое атмосферы, особенно в районе взлетно-посадочной полосы (ВПП) аэропорта необходимо проводить оперативный мониторинг ветровых характеристик атмосферы на расстоянии от единиц метров до нескольких сотен метров.
Для получения полной информации о скорости ветра необходимо проводить измерения, как минимум, при трех различных положениях зондирующего пучка в пространстве. Для этого используются различные методы сканирования атмосферы. В соответствии с известными методами КДЛ может работать в таких режимах сканирования, как RHI, PPI, VAD, либо их различная комбинация..
1. Range Height Indicator (RHI) – режим, при котором азимутальный угол остается постоянным, а угол места изменяется в определенном диапазоне.
2. Plan Position Indicator (PPI) – режим, при котором угол места остается фиксированным, как правило менее 10°, а азимутальный угол меняется либо во всем возможном диапазоне, либо в выбранном секторе.
3. Velocity Azimuth Display (VAD) – режим измерения производятся на нескольких азимутальных углах (обычно не менее 3) при фиксированном угле места (обычно 20° - 30° от вертикали).
В данной статье рассматриваются в первую очередь методы и алгоритмы обработки сигнала ветрового КДЛ с непрерывным излучением, в котором применяется коническое сканирование приземного слоя атмосферы.
2. Принцип конического сканирования
Как было
сказано выше, для получения полной информации о трех компонентах вектора
скорости ветра в декартовой системе координат 
с
помощью КДЛ необходимо провести измерения, как минимум, при трех различных
положениях зондирующего пучка в пространстве. В соответствии с рисунком 1,
поясняющим принцип конического сканирования атмосферы, на заданной высоте h,
определяемой необходимостью измерения, радиальную составляющую скорости ветра
можно записать следующим образом:
,
где θ - угол азимута лазерного луча, который изменяется в интервале [0;2π), а φ - угол места лазерного луча, изменяющийся в диапазоне [0; π/2].
Таким образом, при измерении радиальной скорости ветра в одной точке записывается только одно уравнение при трех неизвестных. При измерении радиальной составляющей скорости ветра в трех независимых точках в пространстве на заданной высоте для трех неизвестных параметров записывается система из трех независимых уравнений. Решение данной системы уравнений позволяет определить полный вектор скорости ветра. При непрерывном вращении лазерного луча по углу азимута путем отбора его дискретных положений получается переопределенная система уравнений, которая решается методом наименьших квадратов.
Отметим, что измерение полного вектора скорости ветра при коническом сканировании воздушного пространства лазерным лучом на различных высотах достигается путем соответствующего изменения фокусного расстояния оптической системы КДЛ. Ключевым моментом принципа конического сканирования является предположение о “замороженности” ветровых характеристик атмосферы за время сканирования на заданной высоте. Поэтому в разработанном алгоритме измерение на одной высоте происходит в течение одной секунды.
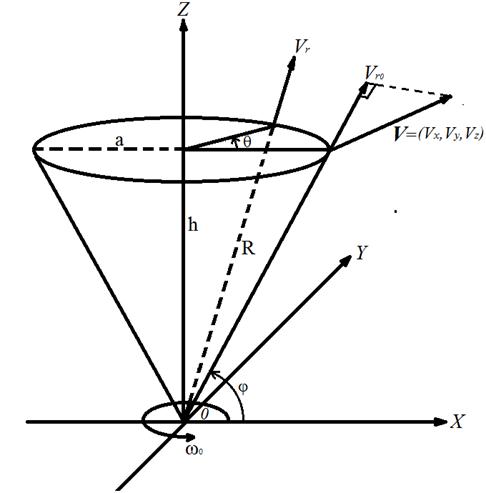
Рисунок 1. Принцип конического сканирования атмосферы лазерным лучом.
В случае, когда ветровые характеристики атмосферы за период полного сканирования лазерным лучом по углу азимута на заданной высоте остаются постоянными, радиальная составляющая вектора скорости ветра изменяется по синусоидальному закону, как это показано на рисунке 2.
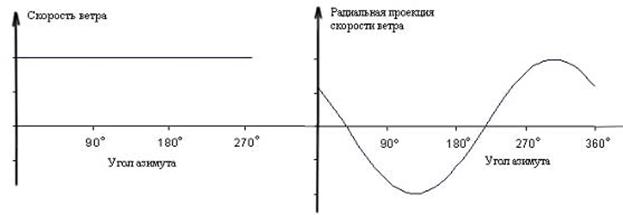
Рисунок 2. Закон изменения радиальной составляющей скорости ветра при постоянстве ветровых характеристик атмосферы при коническом сканировании.
Так как практически осуществляется измерение абсолютных значений доплеровского сдвига частоты, то и полученные результаты должны аппроксимироваться следующей функцией:
,
где a, b– аппроксимирующие коэффициенты.
Направление ветра по азимуту определяется
как угол 
, соответствующий максимальной
положительной скорости. Величина горизонтальной составляющей скорости
определяется амплитудой гармонической функции. Вертикальным смещением
полученного графика определяется величина вертикальной составляющей вектора
скорости.
3. Методы и алгоритмы определения скорости и направления ветра
Основными задачами программно-алгоритмического обеспечения КДЛ являются:
1. Определение спектральных характеристик гетеродинного сигнала на выходе приемного устройства.
2. Обнаружение полезного сигнала в спектральных данных и формирование набора частот, характеризующего скоростные параметры воздушных масс.
3. Подготовка спектральных данных для аппроксимации путем удаления выбросов из набора частот с целью уменьшения ошибочных вычислений параметров ветра.
4. Проведение операции аппроксимации с целью определения искомых параметров функции приближения.
5. Окончательный расчёт параметров ветра.
Блок-схема алгоритма вычисления параметров ветра приведена на рисунке 3.
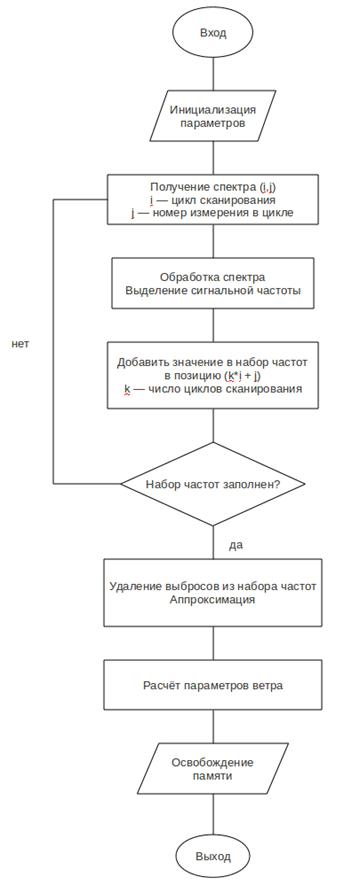
Рисунок 3. - Блок-схема алгоритма вычисления параметров ветра.
Алгоритм вычисления параметров ветра рассмотрим на примере обработки сигнала с профилометра лидарного ветрового ПЛВ-300 [3], разработанного ООО “Лазерные системы” в Санкт-Петербурге.
Сигнал с выхода приемника обратно рассеянного излучения содержит переменную составляющую с частотой до 50 МГц. Обрабатываемая полоса частот непосредственно задается диапазоном скоростей, определяемых лидаром. Аналого-цифровое преобразование осуществляется на частоте 100 МГц. Объем одиночной выборки содержит 512 отсчетов временного сигнала. Длительность выборки по времени – 5.12 мкс. Полученный временной сигнал поступает на блок быстрого преобразования Фурье (БПФ). На выходе блока БПФ вычисляется квадрат модуля комплексного Фурье-спектра.
Квадраты модулей спектров усредняются. Количество спектров в серии – 4096. Общая продолжительность одной серии съема данных - ~21 мс. На рисунке 4 представлена схема обработки сигнала.
Рисунок 4. - Схема обработки сигнала в единичном измерении.
На рисунке 5 показан вид результирующего спектрального сигнала.
Рисунок 5. - Результирующий спектральный сигнал.
Спектр содержит искомую дискретную компоненту в виде колоколообразного импульса. Отношение сигнал/шум находится в диапазоне 3 – 10 для нормальных атмосферных условий с МДВ в диапазоне 7 – 20 км. Ширина сигнала, определяемая по уровню 0.7 от максимального значения, составляет 1 – 5 МГц. Задача алгоритма заключается в поиске дискретной составляющей полезного спектра, определении ее максимального значения и вычислении соответствующей ему частоты доплеровского сдвига:
,
где N0 – положение, соответствующее нулевой скорости ветра.
После этого вычисляется абсолютное значение радиальной составляющей скорости ветра
,
где 
м –
рабочая длина волны КДЛ.
Для выделения полезного сигнала несущего информацию о доплеровском сдвиге частоты, необходимо провести обработку спектра, усредненного за 4096 реализаций. Основные этапы обработки спектра представлены ниже:
1. Нормировка спектра S.
Данная операция позволяет выделить изолинию спектра. Характерный вид спектра с неравномерной фоновой характеристикой показан на рисунке 6. Неравномерность полученного спектра обусловлена шумовыми характеристиками лазера, приемника и трака АЦП.
a) С помощью медианного фильтра с фиксированным окном
спектр сглаживается, из него удаляются резко выделяющиеся значения (в том числе
полезный колоколообразный сигнал). На выходе фильтра получается спектр 
. На рисунке 7 показан сглаженный спектр,
исходный вид которого приведен на рисунке 6.
b) Производится нормировка: 
.
Рисунок 6. - Усреднённый спектральный сигнал.
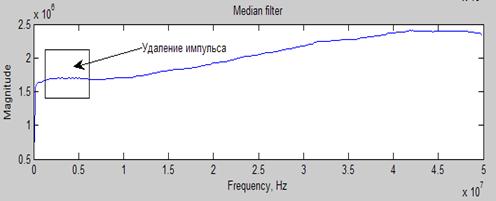
Рисунок 7. - Изолиния спектрального сигнала.
2. Определение частоты доплеровского сдвига 
в спектре полезного сигнала.
a) Выделение полезного колоколообразного сигнала на
нормированном спектре. Для этого производится сглаживание 
“скользящим” или “бегущим” средним с
маленьким окном, чтобы удалить случайные выбросы. В результате на выходе
получается спектр 
, показанный на рисунке 8.
b) Расчет математического ожидания m и
среднеквадратического отклонения s спектра .
Рисунок 8. - Спектральный сигнал
после нормировки и сглаживания.
Для точек
нормированного фильтрованного спектра, удовлетворяющих условию спектра
>
,
рассчитывается центральная частота колоколообразного импульса , множитель k – задает
порог чувствительности и лежит в пределах от 3 до 4, s – стандартное
отклонение, m –
математическое ожидание. Положение центральной частоты рассчитывается в
соответствии с известным центроидным методом по формуле центра масс:
,
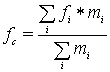где 
–
частота i-й точки спектра,
–
масса i-й точки (значение по амплитуде).
Кроме приведенного выше центроидного метода могут быть использованы такие методы, как метод гауссовой аппроксимации [4] либо метод с использованием порядковых статистик [5].
На рисунке 9 показан уровень
максимума спектрального сигнала и рассчитанный уровень порога 
.
3. Пункты 1 и 2 повторяются для окна медианного фильтра шириной в 2 раза большей. Форма сигнала (ширина колоколообразного импульса) зависит от текущих метеоусловий и может меняться. Алгоритм повторяется с большим окном медианного фильтра, чтобы не пропустить импульсы полезного сигнала различной ширины. Это позволяет использовать алгоритм независимо от текущей формы сигнала.
Применяя алгоритм к полученному спектру в каждой точке сканирующей траектории, получается набор частот, характеризующих поведение ветровых характеристик воздушных масс при сканировании на фиксированной высоте. Графически набор частот показан на рисунке 9.
Рисунок 9. - Результат сканирования на фиксированной высоте.
На рисунке 9 представлен результат сканирования на фиксированной высоте 90 метров в течении нескольких минут. На графике по горизонтальной оси отложены номера точек на кругу сканирования, по вертикальной оси – значения радиальных скоростей, соответствующих центральной частоте найденных на каждом кругу сканирования полезных спектральных сигналов.
4. Алгоритм удаления выбросов из набора частот
В рассматриваемом КДЛ линия зондирования за время ~1 секунду описывает коническую поверхность с углом раствора 22º по отношению к вертикальной оси. Для измерения скорости ветра на заданной высоте осуществляется за один цикл три оборота сканирования. Четвертый оборот используется для определения направления ветра.
Наборы частот с каждого оборота
объединяются в общий массив
по принципу:
,
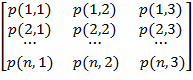где n – число радиальных проекций за один оборот, в качестве столбцов выступает номер оборота.
Спектры радиальных проекций помимо сигнальной составляющей также содержат шум, который в зависимости от атмосферных условий, может в меньшей или большей степени мешать выделению полезного сигнала. Таким образом, в результирующий набор частот попадают нежелательные шумовые частоты, которые должны быть удалены до вычисления параметров аппроксимирующей функции. Это повышает точность аппроксимации, и, соответственно, точность определения параметров скорости ветра.
На рисунке 10 приведена блок-схема алгоритма
удаления выбросов из набора частот. Для удаления выбросов из набора частот рассчитываются
среднее значение (m)
и среднеквадратичное отклонение (s) набора частот . Далее:
1. По порогу отсекаются все точки, амплитуда которых превышает
заданный порог 
, где 
.
2. Оставшиеся точки 
(подмножество ) передаются в алгоритм аппроксимации.
3. На основании результатов аппроксимации формируется вектор 
и вычисляется вектор ошибки аппроксимации
. Если вектор 
содержит
элементы, значение которых превышает три среднеквадратичных отклонения 
, то соответствующие элементы исключаются
из и алгоритм возвращается в начало пункта
3. Другими словами: для каждого 
, исключаются 
из и
повторяется процедура аппроксимации (рисунок 10). В случае успешного
завершения алгоритма удаления выбросов вычисляются параметры гармонической
функции.
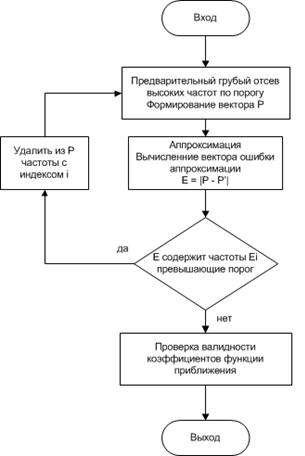
Рисунок 10. - Блок-схема алгоритма удаления выбросов из набора частот.
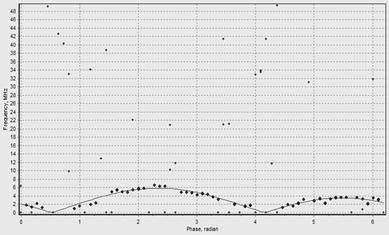
Рисунок 11. - Аппроксимация полученных данных гармонической зависимостью.
Особенностью разработанного алгоритма, является то, что отдельно обрабатывается четвертый оборот сканирования, который предназначен для определения направления ветра, такой подход увеличивает надежность измерений. При анализе данных четвертого оборота учитывается сдвиг всего спектра на половину диапазона спектральной оси. Производится поиск положения пика колоколообразного импульса справа или слева от центральной частоты (25 МГц – середина спектральной шкалы). Алгоритм обнаружения пика аналогичен описанному алгоритму обработки спектров. К имеющейся информации о фазе сигнала добавляется 0 или 180 градусов в зависимости от взаимного положения, обнаруженного на четвертом кругу сканирования пика и центральной частоты спектра.
5. Алгоритм определения параметров аппроксимирующей функции
Аппроксимирующая функция задается выражением:
.
Без потери общности ее общий вид показан на рисунке 12.
Рисунок 12. - Вид аппроксимирующей функции.
Очевидно, выражение для вектора скорости имеет вид:
.
Горизонтальная составляющая вектора скорости:
.
Вертикальная составляющая вектора скорости:
.
Как указывалось выше, на практике имеем:
.
Функция 
зависит от переменной 
и трёх параметров a, b и 
.
Тогда для n измерений за один оборот сканирования можно записать следующее выражение:
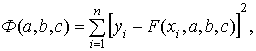
где 
, а 
..
Очевидно, для определения параметров a, b, с в соответствии с методом наименьших квадратов необходимо решить систему уравнений:
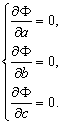
А именно:
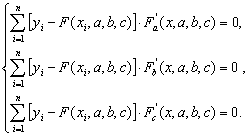
Решение системы уравнений содержит искомые параметры a, b и c, по которым вычисляется горизонтальная и вертикальная составляющие вектора скорости ветра, а также его направление. Отметим, что методы, алгоритмы и сама процедура определения параметров a, b и c в рассмотренной выше постановке детально проработаны в диссертации Смалихо И.Н. [6].
Описанная серия измерений производится при фиксированной фокусировке приемо-передающего телескопа, соответствующей высоте, на которой производятся измерения. Для измерения вертикального профиля скорости ветра эта серия повторяется при нескольких различных фокусировках. Основным конечным результатом измерений является вертикальный профиль скорости ветра, измеренный в нескольких заранее заданных точках по высоте, привязанный к топографическим координатам. Кроме того, должно быть известно, как сориентированы оси x, y относительно направления на север (с точностью 0.2° – 0.3°). Отображение вертикального профиля скорости ветра в зависимости от высоты на мониторе оператора ПЛВ-300 для примера показано на рисунке 13.
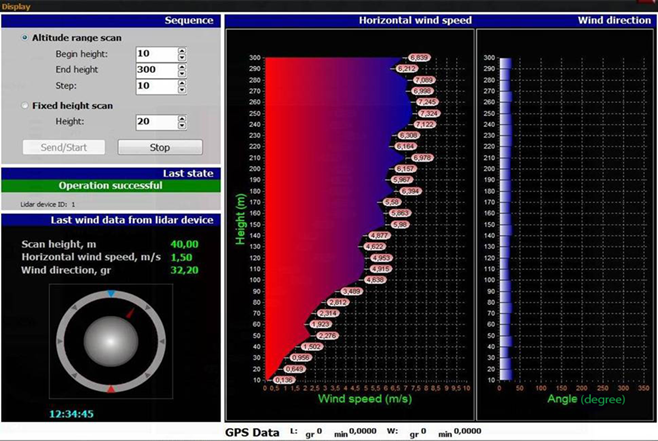
Рисунок 13. - Отображение на мониторе оператора данных о профиле ветра.
6. Выводы
Приведены результаты разработки программно-алгоритмического обеспечения ветрового когерентного доплеровского лидарного профилометра с непрерывным излучением и коническим сканированием атмосферы. Представлены основные принципы, структура и блок-схемы обработки данных с описанием конкретных методов и алгоритмов, которые использованы в профилометре лидарном ветровом ПЛВ-300 разработки ООО “НПП” Лазерные системы”. В результате проведенных испытаний получено, что к достоинствам разработанного программно-алгоритмического обеспечения можно отнести:
- относительную простоту реализации;
- невысокие требования к ресурсам вычислительной системы;
- достаточно высокую помехоустойчивость
- применимость данного алгоритма к различным режимам измерения радиальной скорости.
Полевые испытания показали [7], что ПЛВ-300 в совокупности с разработанным программно-алгоритмическим обеспечением позволяет измерять скорость ветра в диапазоне 1-55 м/с с точностью: абсолютной при V≤ 5 м/с - ±0.5 м/с, относительной при V>5 м/с - ±10%, а направление ветра - в диапазоне 0° - 360° с точностью ±10°.
1. Документ ИКАО: Doc 9426 ICAO, Air Traffic Services Planning Manual, Part II, Chapter 3, Appendix A. ICAO, 2007.
2. Борейшо А.А., Ахметьянов В.Р., Васильев Д.Н., Заморин И.С., Пенкин М.С., Клочков Д.В. Место и роль лидарного профилометра в системе метеообеспечения аэропорта // МЕТЕОСПЕКТР. – 2012. - №4, - С. 62-67.
3. Ахметьянов В.Р., Васильев Д.Н., Клочков Д.В., и др. Доплеровский лидарный профилометр для измерения параметров ветра // Измерительная техника.- 2013. - №6. - С. 35-39.
4. Ахметьянов В.Р., Мишина О.А. Обработка данных ветрового когерентного доплеровского лидара на основе метода гауссовой аппроксимации // Известия вузов. Приборостроение. - 2010. – № 1. – С. 20–26.
5. Ахметьянов В.Р., Мишина О.А. Метод оценивания положения максимума колоколообразной функции с использованием порядковых статистик. // Изв. СПбГЭТУ “ЛЭТИ”. 2010. №7. С. 83-87.
6. Смалихо И.Н. Ветровое зондирование когерентными доплеровскими лидарами: Дис. … доктора физико-математических наук: 01.04.05. – Томск, 2011. – 315 с.
7. Ахметьянов В.Р. Васильев Д.Н. Клочков Д.В. Коняев М.А. и др. Лидарный доплеровский профилометр для измерения параметров ветра в составе наземного комплекса метеорологического обеспечения аэронавигации. Авиакосмическое приборостроение. – 2013, №9, С. 41-52.