Удк 621.3.092
НАВЕДЕНИЕ РАДИОЛУЧА НА ЦЕЛЬ С УЧЁТОМ РЕФРАКЦИИ В АТМОСФЕРЕ ЗЕМЛИ
А. Н. Детков, С. И. Жеребцов, А. Н. Кобузев, И. А. Макаров
ОАО «НПК НИИДАР»,г. Москва
Получена 11 октября 2013 г.
Аннотация. Разработан алгоритм численного моделирования распространения радиолуча в нижней части атмосферы Земли с использованием как невозмущённой, так и возмущённой, произвольно задаваемой, зависимостью коэффициента преломления атмосферы от высоты при задании различных начальных углов места электрической оси антенны, в том числе отрицательные. Предложен способ расчета начального угла места радиолуча, обеспечивающего подсвет цели на заданной высоте и дальностях, включающих «загоризонтные» на базе разработанного алгоритма. Продемонстрированы полученные зависимости конечной высоты радиолуча от начального угла места антенны для технически важных характерных вариантов установки высоты антенны при различных дальностях до цели.
Ключевые слова: рефракция, коэффициент преломления, градиент коэффициента преломления, наведение радиолуча на цель, угол места.
Abstract. The algorithm for the numerical simulation of the propagation of the radio beam in the lower part of the atmosphere of the Earth using both unperturbed and perturbed, arbitrarily defined, the dependence of the refractive index of the height of the atmosphere by setting different starting elevations electrical axis of the antenna, including the negative ones was developed. We propose the method of calculating the initial elevation angle of the radio beam, providing target illumination at a given height and distances, including «the-horizon» on the basis of the algorithm. The dependencies of the final height of the radio beam from the initial elevation of your dish for the technically important characteristic of installation options for various antenna height ranges to the target were demonstrated.
Keywords: refraction, refractive index, gradient of refractive index, the radio beam targeting, the angle of elevation.
Введение
Электромагнитные свойства атмосферы Земли, определяющие условия распространения радиоволн, зависят от диапазона применяемых волн. Для сантиметровых, дециметровых и метровых радиоволн основным параметром состояния атмосферы, влияющим на распространение радиоволн, является градиент коэффициента преломления. Сам коэффициент преломления не постоянен – зависит от состояния атмосферы (например, время суток, сезон года и др.), а также изменяется по трассе распространения радиолуча, т.к. зависит от высоты. Обычно изменение коэффициента преломления по вертикальной координате много больше, чем в горизонтальном направлении [1], поэтому далее в работе будем рассматривать только рефракцию, связанную с высотной зависимостью показателя преломления атмосферы. В работе [2] показано, что решение подобной задачи сводится к двумерной (координаты «высота-дальность»), что не исключает, однако, возможности учёта и боковой рефракции с опорой на полученные ниже алгоритмы.
Известны алгоритмы вычисления вертикального искривления траектории радиолуча за счёт явления рефракции в атмосфере [2-6]. Рассматривая вместо сплошной среды с непрерывно меняющимся показателем преломления слоистую среду, авторы определяют угол преломления радиолуча на каждой границе раздела слоёв по закону Снеллиуса (Snell’s law). Такой конечно-разностный алгоритм расчёта рефракции радиолуча в атмосфере Земли, как показывают численные эксперименты, применим только для вычисления поправок в зоне прямой видимости цели, при положительных значениях начального угла места радиолуча и только для знакопостоянных градиентов показателя преломления по высоте. Первое условие вводит ограничение на распространение радиолуча следующего характера – локационный приёмо-передающий пункт должен располагаться строго ниже цели. Второе условие ограничивает возможность применения такого алгоритма для случая даже слабо возмущённой атмосферы, а не только при аномальной рефракции в ней.
Таким образом, целью данной работы являлось: разработать алгоритм наведения радиолуча на цель в атмосфере Земли для случаев нормального и аномального распределения показателя преломления по трассе распространения, на различных дальностях, как в зоне прямой видимости цели, так и в «загоризонтной» зоне.
Рефракция радиолуча в атмосфере Земли
В атмосфере, представляемой в виде сплошной среды, траектория распространения радиолуча описывается дугой с изменяющимся радиусом кривизны ρ, который определяется на текущем участке траектории через вертикальную проекцию градиента показателя преломления n среды [2]:
где ![]() - приведённый
коэффициент преломления (ПКП),
- приведённый
коэффициент преломления (ПКП), ![]() ,
, ![]() - текущий угол места (угол между
касательной к траектории в данной точке и горизонталью). При отрицательных
значениях
- текущий угол места (угол между
касательной к траектории в данной точке и горизонталью). При отрицательных
значениях ![]() траектория радиолуча искривляется к Земле
(положительная рефракция), а при положительном - от Земли (отрицательная
рефракция).
траектория радиолуча искривляется к Земле
(положительная рефракция), а при положительном - от Земли (отрицательная
рефракция).
Для алгоритма расчета траектории радиолуча используется
зависимость ![]() . Высотный профиль ПКП может быть
рассчитан, например, по модели стандартной атмосферы [7], либо рассчитан методами
интерполяции по отдельным (фиксированным) точкам, полученным с использованием метеорологических
данных [8]. При построении траектории распространения радиолуча в атмосфере будем
использовать как модель «гладкой» зависимости
. Высотный профиль ПКП может быть
рассчитан, например, по модели стандартной атмосферы [7], либо рассчитан методами
интерполяции по отдельным (фиксированным) точкам, полученным с использованием метеорологических
данных [8]. При построении траектории распространения радиолуча в атмосфере будем
использовать как модель «гладкой» зависимости ![]() (соответствующей,
например, стандартной модели атмосферы), так и «возмущенной», в которой
случайное возмущение вносилось путём добавления случайной аддитивной величины со
среднеквадратичным отклонением (СКО) пропорциональным абсолютному значению
приведённого показателя преломления в данной точке на основе обобщённой модели (см.
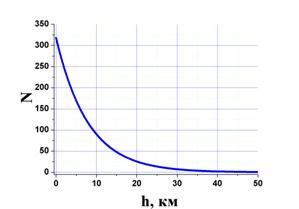
рис. 1). Использование модели возмущенной зависимости
(соответствующей,
например, стандартной модели атмосферы), так и «возмущенной», в которой
случайное возмущение вносилось путём добавления случайной аддитивной величины со
среднеквадратичным отклонением (СКО) пропорциональным абсолютному значению
приведённого показателя преломления в данной точке на основе обобщённой модели (см.
рис. 1). Использование модели возмущенной зависимости ![]() носит,
в том числе, демонстрационную функцию, призванную испытать устойчивость и
надёжность применяемых алгоритмов.
носит,
в том числе, демонстрационную функцию, призванную испытать устойчивость и
надёжность применяемых алгоритмов.
|
|
|
|
а) |
б) |
|
Рис. 1 Зависимость приведённого показателя преломления N от высоты h: а) обобщённая модель атмосферы без возмущения, б) обобщённая модель атмосферы со случайным возмущением (СКО возмущения 0,2). |
|
Алгоритм расчета траектории радиолуча
Расчет одиночной траектории радиолуча, направленного
под произвольным зенитным углом и на заданную дальность производится следующим
образом. Для начальной точки задаётся её высота ![]() , т.е.
высота начала распространения радиолуча или иначе высота расположения антенны,
отсчитываемая от поверхности Земли, и
, т.е.
высота начала распространения радиолуча или иначе высота расположения антенны,
отсчитываемая от поверхности Земли, и ![]() -
начальный зенитный угол радиолуча (антенны), угловая мера которого от начальной
точки до конечной разбивается на достаточно большое количество малых
элементарных частей прямыми, проведенными из центра Земли, с заданным шагом
элементарного угла
-
начальный зенитный угол радиолуча (антенны), угловая мера которого от начальной
точки до конечной разбивается на достаточно большое количество малых
элементарных частей прямыми, проведенными из центра Земли, с заданным шагом
элементарного угла ![]() (где K – количество интервалов
разбиения полного угла от начальной до конечной точки,
(где K – количество интервалов
разбиения полного угла от начальной до конечной точки, ![]() –
радиус Земли, L - длина пути по поверхности Земли между начальной и
конечными точками).
–
радиус Земли, L - длина пути по поверхности Земли между начальной и
конечными точками).
Построение i-ой
элементарной дуги радиолуча является решением геометрической задачи (рис. 2). Пусть
имеется начальная точка ![]() элементарной
дуги на заданной высоте
элементарной
дуги на заданной высоте ![]() (при расчете первой
элементарной дуги
(при расчете первой
элементарной дуги ![]() равна высоте положения фазового
центра антенны относительно центра Земли). Через точку
равна высоте положения фазового
центра антенны относительно центра Земли). Через точку ![]() проведём нормаль к поверхности Земли. В точке
проведём нормаль к поверхности Земли. В точке ![]() рассчитывается по формуле (1) радиус кривизны
траектории
рассчитывается по формуле (1) радиус кривизны
траектории ![]() . От
этой нормали откладывается зенитный угол
. От
этой нормали откладывается зенитный угол ![]() по
часовой стрелке при
по
часовой стрелке при ![]() (против
часовой стрелки при
(против
часовой стрелки при ![]() ) и
проводится соответствующая новая прямая в точке
) и
проводится соответствующая новая прямая в точке ![]() ,
являющаяся касательной к дуге радиолуча в данной точке.
,
являющаяся касательной к дуге радиолуча в данной точке.
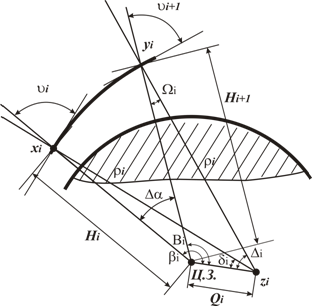
Рис. 2 Геометрия i-ой элементарной дуги траектории радиолуча в атмосфере Земли.
При этом центр ![]() кривизны
элементарной дуги радиолуча лежит на перпендикуляре к полученной касательной на
расстоянии
кривизны
элементарной дуги радиолуча лежит на перпендикуляре к полученной касательной на
расстоянии ![]() от
точки
от
точки ![]() . Из
точки
. Из
точки ![]() проведём дугу окружности радиусом
проведём дугу окружности радиусом ![]() до пересечения со следующей нормалью к поверхности
Земли, отложенной от предыдущей на шаг элементарного угла
до пересечения со следующей нормалью к поверхности
Земли, отложенной от предыдущей на шаг элементарного угла ![]() по ходу распространения радиолуча. В
результате, получим точку
по ходу распространения радиолуча. В
результате, получим точку ![]() и соответствующие ей
новые значения высоты дуги
и соответствующие ей
новые значения высоты дуги ![]() и зенитного угла
и зенитного угла ![]() радиолуча. Из геометрических соображений
следует, что для приведённого на рис. 2 варианта положения точки
радиолуча. Из геометрических соображений
следует, что для приведённого на рис. 2 варианта положения точки ![]() конечные значения высоты
конечные значения высоты ![]() этой дуги и зенитного угла
этой дуги и зенитного угла ![]() радиолуча могут быть рассчитаны на
основании известных значений начальной высоты
радиолуча могут быть рассчитаны на
основании известных значений начальной высоты ![]() дуги и
начального зенитного угла
дуги и
начального зенитного угла ![]() по формулам (2) – (3):
по формулам (2) – (3):
![]() ,
(2)
,
(2)
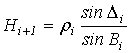 , (3)
, (3)
где ![]() - высота начала i-ой
дуги, отсчитываемая от центра Земли (Ц.З.),
- высота начала i-ой
дуги, отсчитываемая от центра Земли (Ц.З.), 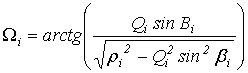 ,
, ![]() ,
, ![]() ,
, 
![]() ,
, ![]() ,
, 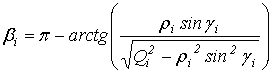 ,
, ![]() .
.
В конце K-го цикла расчета по данному алгоритму рассчитывается
высота![]() и, следовательно, высота
и, следовательно, высота ![]() конечной точки на заданной дальности по
поверхности Земли для заданной начальной высоты
конечной точки на заданной дальности по
поверхности Земли для заданной начальной высоты ![]() радиолуча
и начального зенитного угла
радиолуча
и начального зенитного угла ![]() .
.
Результаты моделирования распространения радиолуча
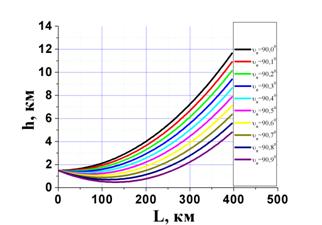
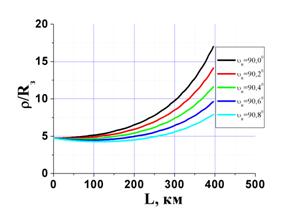
На основе изложенного выше алгоритма производилось моделирование распространения пучка радиолучей с различными начальными азимутальными углами в нижней атмосфере Земли (Рис. 3-5). Наименьший зенитный угол для крайнего радиолуча в пучке составлял 90о, при этом последующим азимутальным углам соответствовали отрицательные углы места. Видно, что даже при СКО возмущения 0,2 траекторные зависимости высоты радиолуча от дальности не сильно отличаются от случая невозмущённой атмосферы (рис. 3). Так на дальностях L=400 км для возмущённой атмосферы расхождение лучей по сравнению с невозмущённой атмосферой составило около 1 км. Вместе с тем, установлено, что градиент показателя преломления (Рис. 4) и радиусы кривизны траектории (Рис. 5) существенным образом зависят от наличия возмущения показателя преломления по трассе.
|
|
|
|
а) |
б) |
|
Рис. 3 Траекторные зависимости высоты h
от дальности L по Земле при распространении радиолуча в атмосфере
при различных начальных зенитных углах |
|
|
|
|
|
а) |
б) |
|
Рис. 4 Типичные траекторные
зависимости градиента приведённого показателя преломления |
|
|
|
|
|
а) |
б) |
|
Рис. 5 Траекторные
зависимости радиуса кривизны
|
|
Алгоритм расчета начального угла места
Описанный выше алгоритм расчёта траектории радиолуча
может быть использован для расчёта начального угла места радиолуча, под которым
его надо направить, чтобы попасть на заданной дальности в точку, находящуюся на
заданной высоте, например, с помощью метода дихотомии. Для этого зададим
начальный интервал поиска от 0 до 2π/3, в котором может находиться искомый
зенитный угол ![]() . Начальный интервал зенитных
углов делится пополам и для полученного зенитного угла равного π/3
рассчитывается высота конечной точки радиолуча hрас. Если расчётная высота конечной точки не попадает в
заданный интервал высот
. Начальный интервал зенитных
углов делится пополам и для полученного зенитного угла равного π/3
рассчитывается высота конечной точки радиолуча hрас. Если расчётная высота конечной точки не попадает в
заданный интервал высот![]() , где
, где ![]() - задаваемая
пользователем точность попадания радиолуча в точку, то в зависимости от знака выражения
- задаваемая
пользователем точность попадания радиолуча в точку, то в зависимости от знака выражения
![]() задается следующий угол
задается следующий угол ![]() : если
: если ![]() , делим пополам интервал зенитных углов от 0 до
π/3 (
, делим пополам интервал зенитных углов от 0 до
π/3 (![]() ), иначе – делим пополам интервал от π/3 до 2π/3 (
), иначе – делим пополам интервал от π/3 до 2π/3 (![]() ). Далее проводим снова расчет высоты конечной точки
радиолуча. Данный расчет повторяется, пока расчётная высота конечной точки не
попадает в заданный интервал высот. Начальный угол места установки электрической
оси антенны вычисляется по последнему значению зенитного угла:
). Далее проводим снова расчет высоты конечной точки
радиолуча. Данный расчет повторяется, пока расчётная высота конечной точки не
попадает в заданный интервал высот. Начальный угол места установки электрической
оси антенны вычисляется по последнему значению зенитного угла: ![]() . Заметим, что рассмотренный простейший метод
двухточечной дихотомии с разбивкой интервала на две половины в подобных
задачах, может приводить к зацикливанию процесса поиска решения и к остановке
сходимости последовательности длин разбиваемых интервалов. Поэтому в алгоритме
расчёта угла места нами применялся также метода поиска решения с использованием
многоточечной дихотомии.
. Заметим, что рассмотренный простейший метод
двухточечной дихотомии с разбивкой интервала на две половины в подобных
задачах, может приводить к зацикливанию процесса поиска решения и к остановке
сходимости последовательности длин разбиваемых интервалов. Поэтому в алгоритме
расчёта угла места нами применялся также метода поиска решения с использованием
многоточечной дихотомии.
Алгоритм расчёта угла места может быть использован, например, в программе управления приводом остронаправленной антенны при организации высокоскоростного канала передачи информации. Программа управления, использующая данный алгоритм, позволяет решать задачу наведения радиолуча антенны на цель (самолет), используя целеуказания – географические координаты, позволяющие по этим данным и координатам места установки антенны рассчитывать начальный угол места электрической оси антенны, на который её нужно установить с помощью поворотного устройства для нацеливания. Данные о положении цели обычно получаются по низкоскоростному каналу связи.
Результаты расчета начального угла места
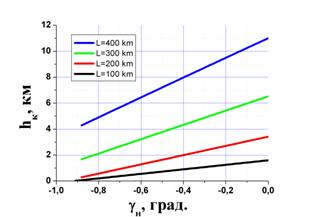
С помощью алгоритма расчета начального угла места получены зависимости конечных высот целей, подсвечиваемых радиолучом, от его начального угла места при различных дальностях до цели, включая «загоризонтные» для двух характерных случаев начальных высот 50 м и 1000 м (Рис. 6). Начальные высоты радиолуча порядка десятков метров могут отвечать ситуации установки антенны, например, на вышке, а начальные высоты около километра – на какой-либо возвышенности или на воздушном носителе (аэростат, вертолёт и т.д.). Нижние границы полученных значений углов места соответствуют минимальным значениям, при которых радиолуч при заданных условиях распространения не утыкается в Землю.
|
|
|
|
а) |
б) |
|
Рис. 6 Зависимости конечной
высоты hк
радиолуча от начального угла места
|
|
Заключение
Разработан алгоритм расчета траектории распространения радиолуча в нижней части атмосферы Земли с использованием как невозмущённой, так и возмущённой зависимостью коэффициента преломления атмосферы от высоты при произвольных начальных углах места электрической оси антенны, включая отрицательные.
В процессе моделирования подтверждена устойчивость созданного алгоритма расчета траектории распространения радиолуча в нижней части атмосферы Земли не только в условиях знакопеременного градиента показателя преломления по трассе, но и в условиях его значительного возмущения.
Разработан алгоритм расчета начального угла места электрической оси антенны для «нацеливания» радиолуча на цель, находящуюся на заданной высоте и расстоянии, включая случай загоризонтной дислокации.
Анализ результатов и скорости работы алгоритмов, методически объединённых в одну программу, позволяют допустить возможность их эффективного использования в технической задаче наведения радиолуча антенны на цель в режиме реального времени, а также в качестве наглядного средства обучения.
1. Колосов М.А., Неон А.А., Яковлев О.И. Распространение радиоволн при космической связи. М.: Изд. «Связь», 1968. 156с.
2. Чёрный Ф.Б. Распространение радиоволн. М.: Изд. «Советское радио», 1972. 464с.
3. Fortunati S., Gini F., Greco M.S., Farina A. , Graziano A., Giompapa S., Castella, F.R. Correction of Refracted Propagation Effects for Airborne Radar Tracking // IEEE Transactions on Aerospace and Electronic Systems. – 2013. v. 49. – № 1. – Р. 20 – 41.
4. Соколов К.С., Трекин В.В., Оводенко В.Б., Патронова Е.С. Метод оперативного учета влияния среды на траекторные измерения // Успехи современной радиоэлектроники. – 2012. – № 2. – С.17 – 21.
5. Оводенко В. Б., Патронова Е. С., Соколов К. С., Трекин В. В. Анализ влияния кратковременных вариаций метеопараметров на ошибки измерения координат в РЛС // Журнал радиоэлектроники: электронный журнал. 2013. №6. URL: http://jre.cplire.ru/jre/jun13/2/text.pdf
6. Родос Л.Я. Электродинамика и распространение радиоволн. – СПб.: Изд. «СЗТУ», 2007.
7. Седунов Ю. С. Атмосфера: справочник. – Л.: Гидрометеоиздат, 1991.
8. Бин Б.Р., Даттон Е.Дж. Радиометеорология. Л.: Изд. «Гидрометиздат», 1971. 363с.