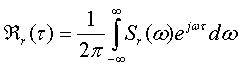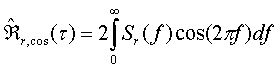УДК 621.391, 621.396
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ШУМОВОЙ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ С РАСШИРЕНИЕМ СПЕКТРА
В. И. Калинин, Д. Е. Радченко, В. А. Черепенин
Институт радиотехники и электроники им.
В.А.Котельникова РАН, Фрязинский
филиал
Статья получена 2 октября 2014 г.
Аннотация. Проведено численное моделирование сверхширокополосной (СШП) шумовой системы передачи информации с расширением спектра. Внесение цифровой информации выполняется в процессе кодовой спектральной модуляции СШП шумовых сигналов. Когерентное сжатие СШП шумовых сигналов в приемнике производится в результате двойной спектральной обработки. Исследованы спектральные и корреляционные характеристики принятых СШП шумовых сигналов при передаче бинарной информации в канале с аддитивной гауссовой помехой.
Ключевые слова: сверхширокополосные системы связи, шумовые сигналы, расширение спектра, корреляция, модуляция, численное моделирование.
Abstract. Numerical simulation of ultra wideband (UWB) noise communications based on spread spectrum technique is performed. Digital information is inserted into continuous noise signals in result of code spectral modulation. Coherent compression of UWB received noise signals is accomplished by means of double spectral processing. Spectral and correlation performance of UWB communication system is investigated for single-ray channel with additive Gaussian white noise.
Key words: ultra wideband communication systems, noise signals, spread spectrum, correlation, modulation, numerical simulation.
Введение
Телекоммуникационные системы с расширением спектра (SSC-Spread Spectrum Communications) характеризуются высокой скоростью передачи данных, помехоустойчивостью и электромагнитной совместимостью [1-6]. В работах [7-9] предложен способ беспроводной передачи цифровой информации с расширением спектра на основе СШП непрерывных шумовых сигналов с разделением по временной задержке информационных и опорного шумовых сигналов, излучаемых в линию связи. На экспериментальной установке микроволнового диапазона показана возможность кодовой спектральной модуляции в приемнике согласно потоку двоичных информационных символов и когерентного сжатия СШП шумовых сигналов в приемнике в результате двойной спектральной обработки с последующим восстановлением передаваемой информации [8,9]. Вероятностные характеристики шумовой системы связи с расширением спектра и временным разделением шумовых сигналов исследованы в работах [10-13]. Перспективным применением помехоустойчивой и скрытной системы связи с низким уровнем шумовых излучений являются беспроводные локальные сети терагерцового диапазона, в котором создание источников излучений с мощностью свыше 10 мВт является сложной задачей [14,15].
Известны системы беспроводной передачи информации на основе хаотических сигналов с амплитудной импульсной модуляцией и энергетическим приемом, которые используют простые схемы построения прямохаотических приемопередатчиков с низким энергопотреблением в беспроводных сверхширокополосных сенсорных сетях [16-18].
В данной работе численными методами проведено исследование канала СШП шумовой радиосвязи с аддитивным гауссовским белым шумом (АГБШ). При численном моделировании выполнен детальный анализ автокорреляционной функции принятых СШП шумовых сигналов.
СШП телекоммуникационная система
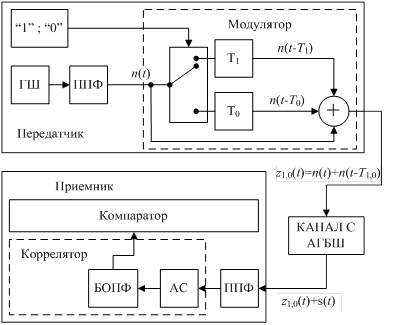
Функциональная схема беспроводной шумовой системы связи, представленная на рис.1, содержит передатчик с кодовой спектральной модуляцией и приемник с двойной спектральной обработкой СШП шумовых сигналов [8,15].
Рис.1. Функциональная схема СШП беспроводной шумовой системы связи.
Генератор шума в
передатчике формирует цифровой случайный сигнал с частотой дискретизации fd = 10 ГГц в виде белого шума с
нормальным распределением амплитуд. Шаг дискретизации между соседними дискретными
отсчетами составляет величину td = 1/fd = 0.1 нсек. Шумовой случайный сигнал поступает на вход цифрового полосно-пропускающего
фильтра (ППФ), на выходе которого формируется шумовой сигнал в виде нормального
случайного процесса n(t) с нулевым средним значением
(рис.2а), равномерным спектром Sn(f) с полосой частот Df = 1000 MHz в
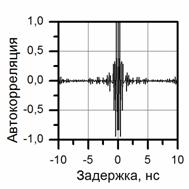
диапазоне 3100–4100 МГц (рис.2б) и быстроспадающей корреляцией ![]() за малое время когерентности
за малое время когерентности ![]() (рис.2в). Здесь дисперсия
(рис.2в). Здесь дисперсия ![]() характеризует среднюю мощность случайного
сигнала n(t). Частотный диапазон 3100–4100 МГц для системы связи выбирался
исходя из требований к частотному ресурсу при безлицензионном использовании СШП
сигналов с низкой мощностью изотропных излучений, которая не превышает
установленный порог [16-17].
характеризует среднюю мощность случайного
сигнала n(t). Частотный диапазон 3100–4100 МГц для системы связи выбирался
исходя из требований к частотному ресурсу при безлицензионном использовании СШП
сигналов с низкой мощностью изотропных излучений, которая не превышает
установленный порог [16-17].
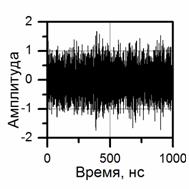
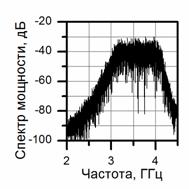
а) б) в)
Рис.2. Временная реализация (а), спектр мощности (б), автокорреляционная функция (в) для непрерывного опорного шумового сигнала в течение 1 мкс.
Частота дискретизации fd = 10 ГГц превышает более чем в два раза верхнюю частоту fm = 4.1 ГГц в спектре сигнала на рис.2. При условии fd > 2 fm справедливо представление непрерывных шумовых сигналов в виде дискретных во времени отсчетов согласно теореме Котельникова-Найквиста [20-21]. Шаг дискретизации во времени для шумовых сигналов устанавливается равным td = 1/fd = 0.1 нс. Временные реализации цифрового сигнала (рис.2а) содержат Nb = Tb/td случайных отсчетов на длительности Тb информационного бита. Скорость передачи Сb = 1/Тb двоичных битов составляет в численном эксперименте величину Cb = (1-2) Мб/с. При передаче информации с указанной скоростью используется Nb= fd/Cb= (5-10)×103 дискретных отсчетов шумового сигнала на длительности каждого бита. Все реализации случайного сигнала в потоке информационных битов являются взаимно ортогональными [12].
Шумовой сигнал n(t) с выхода цифрового ППФ фильтра в передатчике поступает на вход спектрального модулятора, в котором разделяется на информационный и опорный сигналы (рис.1). Модулятор содержит две линии задержки и опорный канал. Информационный шумовой сигнал задерживается в первой линии на время Т1 = 6 нс при поступлении символа “1”, либо в другой линии на время Т0 = 9 нс при поступлении символа “0”. Переключение линий задержки Т1, либо Т0 производится согласно потоку двоичных битов «1»; «0» от источника информации. Процесс переключения каналов отображается ключевой схемой на рис.1. При численном моделировании полагаем, что коэффициенты передачи H10=h10 exp(iθ10) и задержки T10 обеих линий не зависят от частоты f в полосе Δf шумового сигнала n(t) так, что выполняются условия:
В линейном сумматоре происходит сложение опорного сигнала n(t) с одним из шумовых сигналов, задержанных на время Т1, либо Т0 в зависимости от поступающих символов “1”, либо “0”.
На рис.3а,б изображены реализации суммарного СШП шумового сигнала на длительности Tb при внесении «1» бита (а), либо «0» бита (б), которые передаются со скоростью Cb = 1 Мб/с на основе опорного шумового сигнала n(t). Реализации (а) и (б) суммарного СШП шумового сигнала при передаче различных битов в линии связи не отличаются по виду от флуктуационного шума, что свидетельствует о низкой вероятности перехвата (Low Probability Interception-LPI) передаваемой информации и о высокой информационной скрытности СШП шумовой системы связи [4,6].
а) б)
Рис.3. Реализации суммарного шумового сигнала при передаче «0» и «1» символов.
Спектр мощности суммарного шумового сигнала z10(t), вычисляемый за время следования Tb одного информационного символа, модулирован периодической функцией в виде
Здесь ![]() и
и ![]() являются случайными оценками спектра
мощности для суммарного z10(t) и опорного n(t)
СШП шумовых сигналов за конечное время анализа Tb.
являются случайными оценками спектра
мощности для суммарного z10(t) и опорного n(t)
СШП шумовых сигналов за конечное время анализа Tb.
Суммирование полностью
некогерентных сигналов имеет место, когда задержки Т1 и Т0
информационных сигналов n(t-T1) и n(t-T0) относительно опорного сигнала n(t) значительно превышают время когерентности ![]() СШП шумового сигнала n(t)
СШП шумового сигнала n(t)
При интерференции
полностью некогерентных шумовых сигналов [7-9], когда выполняется условие (4),
спектральная плотность (3) модулируется гармонической функцией в зависимости от
частоты f с масштабом периодичности, равным
![]() .
.
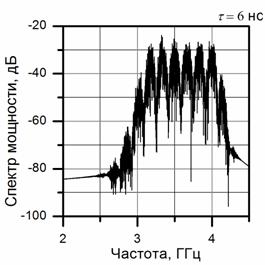
На рисунке 4а,б
представлены спектры мощности суммарных шумовых сигналов, поступающих в линию
при передаче двоичных символов. Спектры мощности на рис.4а,б, вычисленные за
конечное время Tb=1 мкс,
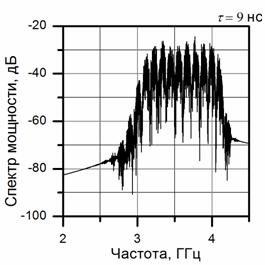
являются случайными функциями. Полоса частот шумовых сигналов составляет Df = 1000 МГц и время когерентности порядка ![]() . При передаче двоичного символа «0» задержка
сигнала в модуляторе составляет Т0 = 9 нс, тогда
период спектральной модуляции равен df0 = 1/Т0 = 111 МГц.
При передаче бита «1» задержка составляет Т1 = 6 нс и
период спектральной модуляции равен df1 = 1/Т1 = 167 МГц.
. При передаче двоичного символа «0» задержка
сигнала в модуляторе составляет Т0 = 9 нс, тогда
период спектральной модуляции равен df0 = 1/Т0 = 111 МГц.
При передаче бита «1» задержка составляет Т1 = 6 нс и
период спектральной модуляции равен df1 = 1/Т1 = 167 МГц.
а) б)

в) г)
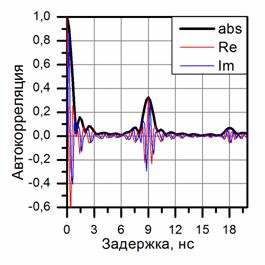
Рис.4. Спектры мощности (а,б) с кодовой спектральной модуляцией и комплексные автокорреляционные функции (в,г) при передаче «1» символа (а,в) и «0» символа (б,г). Цветными линиями изображены действительная (красным) и мнимая (синим) части, черной жирной линией- модуль для комплексной автокорреляционной функции (в,г).
Активные помехи в канале передачи отсутствуют.
Спектр двоичных битов, передаваемых со скоростью Сb=(1-2) Мб/с, занимает полосу частот F=1/Тb=(1-2) MГц. В результате кодовой спектральной модуляции происходит расширение спектра передаваемой цифровой информации до полосы частот Df = 1000 МГц СШП шумовых сигналов в B = Df/F= DfTb = (500-1000) раз. Произведение B = DfTb определяет базу (processing gain) сложного сигнала z10(t) и характеризует помехоустойчивость системы передачи информации [4].
Мощность суммарного
шумового сигнала z10 (t) определяется его дисперсией ![]() и равна удвоенной мощности
и равна удвоенной мощности ![]() исходного шумового сигнала n(t) при условии полной некогерентности опорного и
задержанных шумовых сигналов.
исходного шумового сигнала n(t) при условии полной некогерентности опорного и
задержанных шумовых сигналов.
Приемник СШП телекоммуникационной системы
Суммарный сигнал z10 (t) с кодовой спектральной модуляцией (рис.4а,б) поступает с выхода передатчика в канал связи с аддитивным гауссовым белым шумом (АГБШ). Полагаем коэффициент передачи канала связи не зависящим от частоты и равным единице в полосе Δf шумового сигнала n(t). Принятый сигнал в виде аддитивной смеси суммарного сигнала и гауссовой помехи поступает на вход цифрового ППФ фильтра с такой же полосой пропускания Δf, как в передатчике. На выходе цифрового ППФ фильтра формируется сигнал
r(t) = z10(t) + s(t) = [n(t) + n(t- T10)] + s(t) (5)
в виде суммы передаваемого шумового
сигнала z10(t) с кодовой спектральной модуляцией и
согласованной по спектру гауссовой помехи s(t)
с дисперсией ![]() быстроспадающей корреляцией
быстроспадающей корреляцией ![]() и равномерным спектром
и равномерным спектром ![]() в той же полосе частот Δf как у полезного сигнала z10(t).
в той же полосе частот Δf как у полезного сигнала z10(t).
Отношение сигнал/помеха (channel SNR) на входе приемника определяется отношением мощности принятого сигнала и гауссовой помехи в виде:
Полагаем полезный шумовой сигнал z10(t) и случайную помеху s(t) полностью некогерентными между собой. Тогда спектр мощности для принятого сигнала r(t) определяется в виде:
Спектр (7) содержит функцию,
периодически модулированную по частоте согласно потоку битов, и аддитивную
добавку ![]() в виде спектра помехи. В формуле (7)
спектры
в виде спектра помехи. В формуле (7)
спектры ![]() ,
, ![]() и
и ![]() для принятого сигнала r(t), опорного сигнала n(t)
и помехи s(t), являются случайными оценками за конечное время
длительности бита Тb
передаваемой информации.
для принятого сигнала r(t), опорного сигнала n(t)
и помехи s(t), являются случайными оценками за конечное время
длительности бита Тb
передаваемой информации.
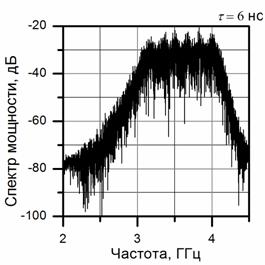
На рис.5а,б представлен
спектр мощности ![]() принятого сигнала (5) при
воздействии АГБШ помехи, когда отношение сигнал/помеха в канале (6) равно q = -5дБ.
принятого сигнала (5) при
воздействии АГБШ помехи, когда отношение сигнал/помеха в канале (6) равно q = -5дБ.
а) б)
в) г)
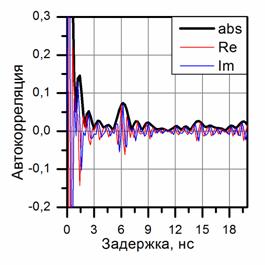
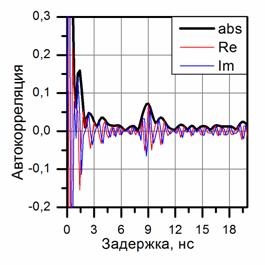
Рис.5. Спектры мощности (а,б) и комплексные автокорреляционные функции (в,г) при передаче «1» символа (а,в) и «0» символа (б,г) в канале с АГБШ помехой. Цветными линиями изображены действительная (красным) и мнимая (синим) части, черной жирной линией - модуль для автокорреляционной функции (в,г). Отношение сигнал/помеха в канале равно q = -5дБ.
Прием слабого полезного сигнала z10(t) производится «глубоко под тепловыми шумами» при отрицательном значении q < 0.0дБ отношения сигнал/помеха в канале. Сильные помехи эффективно маскируют периодическую модуляцию в спектре принятого сигнала так, что внешнему наблюдателю визуально трудно выделить информационную периодическую составляющую в спектре на фоне маскирующих помех при передаче двоичных битов, как изображено на рис. 5а,б при воздействии помех, превышающих полезный сигнал z10(t) по мощности в три раза, q = -5дБ. В работах [7-10,14-15] предложено решение задачи о выделении информационных сообщений, передаваемых на основе СШП шумовых сигналов в канале связи с АГБШ помехами, методом обратного преобразования Фурье от измеренного спектра мощности (7) для принятого сигнала (5).
Когерентная обработка СШП шумовых сигналов
В приемнике производится
когерентное сжатие принятых СШП шумовых сигналов (5) в полосу частот передаваемых
сообщений в результате двойного
спектрального анализа (double spectral
processing) [7-10]. Согласно теореме Винера – Хинчина
[20-21] искомую корреляцию ![]() можно вычислить в
результате обратного преобразования Фурье от измеренного спектра мощности Sr(ω), ω=2πf принятого сигнала r(t)
можно вычислить в
результате обратного преобразования Фурье от измеренного спектра мощности Sr(ω), ω=2πf принятого сигнала r(t)
Комплексная автокорреляционная функция, вычисленная по формуле (8) с использованием выражения (7) для спектра мощности принятого сигнала (5), имеет вид:
Комплексная автокорреляционная
функция (9) принятого сигнала в канале с АГБШ имеет информационный
корреляционный пик ![]() со сдвигом Т1,
либо Т0 согласно потоку двоичных битов (1;0). Автокорреляционная
функция (9) содержит также автокорреляционные функции
со сдвигом Т1,
либо Т0 согласно потоку двоичных битов (1;0). Автокорреляционная
функция (9) содержит также автокорреляционные функции ![]() и
и
![]() для опорного шумового сигнала n(t) с удвоенной мощностью
для опорного шумового сигнала n(t) с удвоенной мощностью ![]() и АГБШ
внешней помехи s(t) с мощностью
и АГБШ
внешней помехи s(t) с мощностью ![]() .
.
Коррелятор в приемнике на рис.1 содержит цифровой анализатор спектра – АС и цифровой Фурье процессор – БОФП. На выходе цифрового анализатора спектра в течение Tb каждого передаваемого бита определяется спектр мощности принятого шумового сигнала в виде (9). Цифровой Фурье процессор осуществляет быстрое обратное преобразование Фурье для массива цифровых отсчетов, которые формируются на выходе анализатора спектра АС. В результате двойной спектральной обработки за время следования каждого бита информации определяются квадратурные компоненты для комплексной автокорреляционной функции (9) в виде
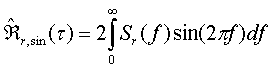 (10б)
(10б)
Модуль для комплексной автокорреляционной функции (9) вычисляется как среднее квадратичное значение от действительной (10а) и мнимой (10б) частей в виде
Компаратор на выходе цифрового
Фурье процессора (рис.1) производит сравнение информационных корреляционных
пиков со сдвигами Т1, либо Т0 для модуля
(11) и выделяет из них наибольший по величине корреляционный пик, отвечающий
передаваемому биту «1», либо «0». Таким образом, в приемнике происходит
однозначное восстановление передаваемой бинарной информации. Воздействие
внешней АГБШ помехи в канале связи сопровождается ростом случайных выбросов
для автокорреляционной функции ![]() в области
информационных пиков
в области
информационных пиков ![]() со сдвигом τ
= T10 , что приводит к увеличению ошибки
при восстановлении в приемнике передаваемой бинарной информации [10,12].
со сдвигом τ
= T10 , что приводит к увеличению ошибки
при восстановлении в приемнике передаваемой бинарной информации [10,12].
Действительная ![]() и мнимая
и мнимая ![]() квадратурные
компоненты (рис.4а,б и рис.5а,б) для комплексной автокорреляционной функции (9)
сильно отличаются друг от друга и испытывают знакопеременные биения при
изменении задержки
квадратурные
компоненты (рис.4а,б и рис.5а,б) для комплексной автокорреляционной функции (9)
сильно отличаются друг от друга и испытывают знакопеременные биения при
изменении задержки ![]() в пределах информационных корреляционных
пиков со сдвигом
в пределах информационных корреляционных
пиков со сдвигом ![]() , что усложняет процедуру
последующего выделения передаваемой информации [12]. Вычисление действительного
модуля (11) за конечное время анализа Tb, равное длительности одного бита, дает сглаженную и
случайную оценку [8-9] для комплексной автокорреляционной функции (9) для всех
значений аргумента τ, как изображено на рис.4в,г при отсутствии
внешних помех и на рис. 5в,г при воздействии АГБШ помехи в канале связи.
, что усложняет процедуру
последующего выделения передаваемой информации [12]. Вычисление действительного
модуля (11) за конечное время анализа Tb, равное длительности одного бита, дает сглаженную и
случайную оценку [8-9] для комплексной автокорреляционной функции (9) для всех
значений аргумента τ, как изображено на рис.4в,г при отсутствии
внешних помех и на рис. 5в,г при воздействии АГБШ помехи в канале связи.
Уровень случайных боковых
выбросов для модуля ![]() зависит от сдвига τ.
При воздействии внешних помех уменьшается относительная величина информационных
пиков со сдвигами τ =T10 на рис.5в,г по сравнению с рис.4в,г, когда внешние помехи отсутствуют.
В численном эксперименте наблюдаются аномально большие боковые выбросы для модуля
зависит от сдвига τ.
При воздействии внешних помех уменьшается относительная величина информационных
пиков со сдвигами τ =T10 на рис.5в,г по сравнению с рис.4в,г, когда внешние помехи отсутствуют.
В численном эксперименте наблюдаются аномально большие боковые выбросы для модуля
![]() при кратных сдвигах τ = jT10 (j=2,3,4), и прежде всего при удвоенной кратности
задержек τ = 2T10 как при
отсутствии внешних помех (рис.4в,г), так и при воздействии АГБШ помехи
(рис.5в,г) в канале связи.
при кратных сдвигах τ = jT10 (j=2,3,4), и прежде всего при удвоенной кратности
задержек τ = 2T10 как при
отсутствии внешних помех (рис.4в,г), так и при воздействии АГБШ помехи
(рис.5в,г) в канале связи.
На рис. 4(в,г)
представлен вторичный спектр для принятого шумового сигнала r(t), изображенного на рис. 3а,б при отсутствии АГБШ
помехи в канале связи. Вторичный спектр вычислен за время следования Tb=1мкс информационного бита в
результате компьютерного моделирования шумовой системы связи при передаче
двоичных битов на основе СШП непрерывных шумовых сигналов в частотном диапазоне
3100-4100 МГц. Вторичный спектр определяется модулем (11) автокорреляционной
функции ![]() , которая находится согласно формуле Винера-Хинчина
(8). Квадратурные компоненты
, которая находится согласно формуле Винера-Хинчина
(8). Квадратурные компоненты ![]() и
и ![]() комплексной автокорреляционной функции
комплексной автокорреляционной функции ![]() определяются методом быстрого обратного
преобразование Фурье, используя базисные функции cos(ωτ) и sin(ωτ), от спектра мощности (3) для принятого
сигнала [20]. На рис. 4а,б представлен спектр мощности с кодовой спектральной
модуляцией, период которой равен df1 = 167 МГц при передаче символа «1»,
либо df0 = 111 МГц при передаче символа «0». Вторичный
спектр, изображенный на рис. 4в,г, определяется в виде среднее квадратичного
значения (11) от квадратурных компонент
определяются методом быстрого обратного
преобразование Фурье, используя базисные функции cos(ωτ) и sin(ωτ), от спектра мощности (3) для принятого
сигнала [20]. На рис. 4а,б представлен спектр мощности с кодовой спектральной
модуляцией, период которой равен df1 = 167 МГц при передаче символа «1»,
либо df0 = 111 МГц при передаче символа «0». Вторичный
спектр, изображенный на рис. 4в,г, определяется в виде среднее квадратичного
значения (11) от квадратурных компонент ![]() и
и ![]() , найденных таким способом в численном
эксперименте.
, найденных таким способом в численном
эксперименте.
Вторичные спектры содержат четко выделенные информационные пики со сдвигом τ = Т1 = 6 нс при передаче «1» бита (рис.4а) и со сдвигом τ = Т0 = 9 нс при передаче «0» бита (рис.4б). Во вторичных спектрах на рис.4а,б выделяются статистически значимые боковые пики с удвоенной τ = 2Т10 задержкой. Боковые выбросы при утроенной задержке τ = 3Т10 характеризуются меньшей амплитудой так, что их трудно идентифицировать за время следования одного бита.
Спектры мощности (а,б) и вторичные спектры (в,г) для принятого шумового сигнала представлены на рис. 5а,б,в,г при воздействии сильной АГБШ помехи, когда прием сигналов производится «под шумами» так, что отношение сигнал/помеха в канале связи меньше единицы и равно q = -5 дБ. Сильная внешняя помеха маскирует информационную составляющую в спектре суммарного сигнала на рис.5а,б так, что кодовая спектральная модуляция визуально не обнаруживается в отличие от спектра на рис. 4а,б с периодической интерференцией, когда отсутствует внешняя помеха. Однако, при воздействии даже сильной внешней помехи q = -5 дБ в результате когерентного сжатия удается надежно выделить во вторичных спектрах статистически значимые информационные пики со сдвигом τ = Т1 = 6 нс при передаче «1» бита (рис.5в) и со сдвигом τ = Т0 = 9 нс при передаче «0» бита (рис.5г). Сравнение вторичных спектров на рисунках 4 и 5 показывает, что внешняя помеха уменьшает относительный вклад информационных пиков со сдвигом τ = Т10 и увеличивает случайную ошибку. Боковые выбросы на кратных задержках τ = jТ10 (j=2,3,4) во вторичных спектрах на рис.5в,г полностью маскируются сильной помехой.
Передача цифровой информации с расширением спектра (Spread Spectrum Noise Communications) осуществляется на основе относительного метода (Transmitted Reference) с разделением опорного и информационных шумовых сигналов по временной задержке [3-4]. В линию связи поступает непрерывный во времени суммарный шумовой сигнал, энергия которого равномерно распределена в текущем времени и в широкой полосе частот. Произведение полосы частот Δf = 1000 МГц и длительности Tb = 1-2 мкс результирующего шумового сигнала или база сигнала (processing gain) B=ΔfTb при передаче двоичных символов достигает большой величины порядка B= 500-1000. Передача информации на основе СШП непрерывных шумовых сигналов с большой базой характеризуется высокой помехоустойчивостью по отношению к внешним помехам и вредной интерференции в каналах с многолучевым распространением.
Заключение
Численное моделирование подтверждает возможность передачи данных со скоростью (1-2) Mб/с на основе непрерывных шумовых сигналов с полосой частот 1000 МГц в микроволновом диапазоне. Показано, что внесение цифровой информации в результате кодовой спектральной модуляции шумовых сигналов в передатчике приводит к расширению спектра передаваемой информации. В линию связи одновременно поступают информационные шумовые сигналы с задержкой согласно передаваемым двоичным символам и опорный шумовой сигнал. Когерентная обработка в приемнике осуществляется синхронно потоку информационных битов методом двойного спектрального анализа, в результате которого определяется комплексная автокорреляционная функция для СШП принятых шумовых сигналов за время следования каждого бита.
Действительная и мнимая составляющие для комплексной автокорреляционной функции существенно отличаются друг от друга и испытывают знакопеременные биения при изменении временного сдвига в пределах информационных корреляционных пиков, что усложняет процедуру последующего выделения передаваемой информации. Вычисление действительного модуля от квадратурных компонент за конечное время длительности бита, дает сглаженную и случайную оценку для автокорреляционной функции как при отсутствии, так при воздействии АГБШ помехи в канале связи.
В численном эксперименте наблюдаются аномально большие боковые выбросы для комплексной автокорреляционной функции при временных сдвигах, кратных информационной задержке, прежде всего при удвоенной кратности задержки.
Компаратор на выходе цифрового Фурье процессора производит сравнение действительных модулей для информационных корреляционных пиков с временными сдвигами согласно потоку битов и выделяет из них наибольший корреляционный пик, отвечающий передаваемому биту. Таким образом, в приемнике происходит однозначное восстановление передаваемой бинарной информации.
Система шумовой радиосвязи с кодовой спектральной модуляцией в передатчике и с двойной спектральной обработкой в приемнике обладает высокой помехоустойчивостью и позволяет осуществлять надежную передачу цифровой информации «под шумами». Результаты численного моделирования могут быть использованы для создания систем шумовой радиосвязи с расширением спектра, предназначенных для применения в персональных локальных WPAN сетях микроволнового и терагерцового диапазонов частот.
Работа выполнена при поддержке гранта РФФИ № 13-07-00903-м и Программы ОФН РАН «Радиовидение».
Литература
1. J.K. Holmes, Coherent Spread Spectrum Systems, Wiley, New York, 1982.
2. B. Sklar, Digital Communications: Fundamentals and Applications, 2nd edition, Prentice-Hall, 2001.
3. Rushforth C.K., Transmitted-reference techniques for random or unknown channels // IEEE Trans. Inf. Theory, 1964, 10 (1), pp.39-42.
4. Семенов А.М., Сикарев А.А. Широкополосная радиосвязь, М.: Воениздат, 1970.
5. Ю.В. Гуляев, В.Я. Кислов, В.В. Кислов, В.И. Калинин, В.В. Колесов, Р.В. Беляев, Г.М. Воронцов, Широкополосные телекоммуникационные средства с кодовым разделением каналов на основе хаотических сигналов // Радиотехника, 2002, № 10, С.3-15.
6. R.M. Narayanan and J. Chuang, Covert communications using heterodyne correlation random noise signals // Electronics Letters, 2007, vol.43, no. 22, pp.1211-1212.
7. Калинин В.И., Спектральная модуляция широкополосных шумовых сигналов // Радиотехника и электроника, 1996, Т. 41, № 4, С.488-493.
8. Калинин В.И., Сверхширокополосная передача информации с двойной спектральной обработкой шумовых сигналов // Письма в ЖТФ, 2005, Том 31, Вып.21, С.58-63.
9. Valery Kalinin, Andrey Panas, Vladimir Kolesov, and Vladimir Lyubchenko, Ultra Wideband Wireless Communication on the Base of Noise Technology // XVI International Conference on Microwaves, Radar and Wireless Communications, MIKON-2006, Poland, Krakow, May 22-24, 2006, Conference Proceedings, Vol. 2, pp. 615-618.
10. Калинин В.И., Чапурский В.В., Черепенин В.А. Вероятностные характеристики для сверхширокополосной шумовой системы связи с кодовой спектральной модуляцией // Доклады VII Всероссийской научно-техн. конференции "Радиолокация и радиосвязь" 25-27 ноября 2013, Москва, с.30-33.
11. Mikhail E. Ilchenko, V. I. Kalinin, T. N. Narytnik, and R. M. Didkovski, Potential Performance of the Communication Systems Using Autocorrelation Reception of Shift-Keyed Noise Signals // Telecommunications and Radio Engineering, 2014, Vol. 73, No. 11, pages 955-976.
12. Калинин В.И., Радченко Д.Е., Влияние межсимвольной задержки на помехоустойчивость системы телекоммуникации с расширением спектра // 16-я Межд. конференция "Цифровая обработка сигналов и ее применение" (DSPA-2014), Москва, 2014, доклады, Т.1, С. 224-227.
13. M. Sushchik, L.S. Tsimring, and A.R. Volkovskii, Performance Analysis of Correlation-Based Communication Schemes Utilising Chaos // IEEE Transactions on Circuits and Systms-I, vol.47, No.12, December 2000, pp.1684-1691.
14. Tiodor. Narytnik, Aladdin Amro, Michael Ilchenko, Valeri Kalinin, Osama Turabi. Sub-Terahertz Low Power UWB Communication Link for WPAN // Network and Complex Systems, 2012, Vol. 2, No. 4, p.45-49.
15. M. E. Ilchenko, V. A. Cherepenin, V. I. Kalinin, T. N. Narytnyk, V. V. Chapurskiy, Wireless terahertz communications with spectral modulation of UWB noise signals // Telecommunication Sciences, 2012, Vol. 3, N. 2, P. 39-43.
16. Дмитриев А.С., Клецов А.В., Лактюшкин А.М., Панас А.И., Старков С.О. "Сверхширокополосные коммуникационные системы на основе динамического хаоса" // Успехи современной радиоэлектроники, 2008, №1, C. 4–16.
17. Ю. В. Андреев, Е. В. Ефремова, В. А. Лазарев, Энергосберегающие режимы приемопередатчиков в сверхширокополосных сенсорных сетях // Журнал Радиоэлектроники, №1, 2012.
18. М.Ye. Ilchenko, Т.N. Narytnik, and R.М.
Didkovsky, Potential
Noise-Immunity of Communications with Power Reception of the Shift-Keyed Noise
Signals //
Telecommunications and Radio Engineering, 2014, Vol. 73, No. 0, p. 777-791.
19. G. Kolumban, M.P.Kennedy, and L.O. Chua, The role of synchronization in digital communications using chaos-Part III: Performance bounds for correlation receivers // IEEE Trans. Circuits Syst. I, vol. 47, no. 12, pp.1673-1683, Dec.2000.
20. Bendat J.S., Piersol A.G. Engineering Applications of Correlation and Spectral Analysis. Wiley – Interscience, New York,1980 [Имеется перевод: Бендат Дж., Пирсол А. Применения корреляционного и спектрального анализа. – М.: Мир, 1983]
21. Тихонов В.И. Статистическая радиотехника, Изд. Советское радио, М., 1966, 677 с.