УДК 538.566
МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ ГЕКТОМЕТРОВЫХ
И БОЛЕЕ ДЛИННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
НАД ПОКРЫТЫМИ ЛЕСОМ ТРАССАМИ
Ю. Б. Башкуев, М. Г. Дембелов
Институт физического материаловедения СО РАН
Статья получена 2 мая 2015 г., после доработки – 28 сентября 2015 г.
Аннотация. В статье представлены результаты моделирования поля земной волны, создаваемой вертикальным электрическим диполем над слоистой структурой «лес-почва». Показано, что в диапазоне 50-200 кГц условия распространения радиоволн над лесом при сильно-индуктивном импедансе более благоприятны, чем над почвой без леса. Получены значения модуля функции ослабления |W|, превышающие единицу и достигающие |W| = 1,74, которые обусловлены поверхностной электромагнитной волной (ПЭВ). При |W| > 1 условия распространения более благоприятны, чем над однородной бесконечно проводящей поверхностью. При анализе численных данных для |W| и уровня поля E на трассах с высотой леса от 7 до 25 метров установлено, что условия распространения радиоволн над лесистыми трассами зависят от частоты, высоты леса и расстояния от излучателя. Результаты моделирования показали сильное влияние лесных массивов на распространение радиоволн СДВ-ДВ диапазонов.
Ключевые слова: поверхностная электромагнитная волна, лесной массив, поверхностный импеданс, удельная проводимость, функция ослабления.
Abstract: Results of modeling of the ground wave field created by vertical electric dipole over layered structure “forest-soil” are offered in the paper. It is shown that conditions of radio wave propagation over forest massif with high inductive impedance in the 50-200 kHz ranges are more favourable than over soil without forest. Values of module of an attenuation function |W| that exceed 1,74 and that was account for by surface electromagnetic wave (SEW) were obtained. For |W| > 1, conditions for propagation are more favorable than over homogeneous conducting surface. After analysis of numerical data for |W| and field level E for paths with forest height from 7 to 25 meters, it is established that conditions of radio wave propagation over forest paths depend on frequency, forest height and distance from transmitter for high inductive surface impedance. Results of modeling have showed profound effect of forest massifs on radio wave propagation in the VLF-MF ranges.
Key words: surface electromagnetic wave, forest massif, surface impedance, conductivity, attenuation function.
Введение
В связи с проблемой поверхностной электромагнитной волны (ПЭВ) большое значение для покрытых лесом районов России имеет исследование распространения гектометровых и более длинных электромагнитных волн над лесистыми трассами. Обзор литературы по лесным территориям показал, что электромагнитные характеристики слоистых структур с резко контрастными электрическими свойствами «лес-почва» и процессы распространения радиоволн над ними исследованы не достаточно полно и глубоко [1-8]. Отличительной чертой лесной среды является наличие случайно расположенных цилиндрических и иных включений. Причем, если в диапазоне длин волн порядка тысяч и сотен метров лес представляет собой достаточно строго организованную электродинамическую структуру из-за преобладающего вклада волн, рассеянных вертикально ориентированными стволами деревьев, то в более коротковолновых диапазонах существенную роль играет переизлучение и рассеяние остальными произвольно ориентированными элементами лесной растительности. В данной статье мы ограничимся рассмотрением модели леса в диапазоне гектометровых и более длинных электромагнитных волн. В работах В.А.Егорова и Г.И. Макарова [4-6] решена задача определения переизлученного деревьями электромагнитного поля в диапазоне волн длиннее 100 м. Численный анализ решения позволил им сделать вывод о том, что влияние растительного покрова может быть учтено в модели однородного изотропного «леса-слоя» с эффективными значениями комплексной диэлектрической проницаемости, которая не зависит от высоты леса, от месторасположения точки наблюдения внутри лесного массива и от густоты расположения деревьев в лесу. Проведенный теми же авторами теоретический анализ результатов экспериментальных исследований искажений электромагнитного поля в присутствии отдельного дерева, являющегося основным элементом растительного покрова, позволил представить дерево в модели вертикального электрического переизлучателя с емкостной нагрузкой. Комплексное сопротивление такого переизлучателя определяется по геометрическим характеристикам ствола и кроны дерева с учетом удельной электрической проводимости древесины ствола дерева, по формулам, справедливым для конденсатора с утечкой, что дает хорошее совпадение теории и эксперимента. Результаты работ [4-6 ] были положены в основу принятой нами модели «лес–почва». Следует отметить, что двухслойная модель «лес-почва» («растительность – грунт») достаточно груба и не полностью учитывает поляризационные свойства стволов леса. В работе [7] для учета этих свойств вводится тензор относительной комплексной диэлектрической проницаемости. Не останавливаясь на практической направленности проведенного моделирования, заметим, что расчеты поверхностного импеданса мы можем проводить для любой n-слойной дискретно-слоистой или градиентной модели подстилающей среды [1]. Двухслойная модель приводит к более наглядному пониманию физических механизмов распространения радиоволн над лесной средой.
Цель работы - моделирование условий распространения электромагнитных волн в диапазоне 50-500 кГц (функция ослабления W, уровень электромагнитного поля Е) над слоистой структурой «лес-почва» в одномерном трассовом приближении, анализ численных данных моделирования.
1. Электрические характеристики лесой растительности
Для прогнозирования распространения СДВ-ДВ радиоволн вдоль покрытой лесом земной поверхности необходимо знать электрические параметры лесной растительности (sл и eл). В литературе имеется ограниченное количество экспериментальных данных [1-7], полученных в различных физико-географических условиях (субтропики, европейская часть России, Сибирь, северная Америка). Известно, что на территории России леса покрывают площадь свыше 7 млн. км2, из них в Прибайкалье и Забайкалье — 960 тыс. км2 (60% территории). Хвойные леса в России представлены, в основном сосной, лиственницей, елью и кедром. Из лиственных пород наиболее широко распространены береза и осина. Высота деревьев изменяется от 7 до 25 м, в среднем 10—20 м; диаметр ствола — от 0,1 до 0,8 м, а среднем 0,15—0,35 м. На открытых местах высота деревьев ниже, чем в густом лесу. Сосновые леса, преобладающие в Сибири, обычно растут на сухих песчаных почвах и южных склонах гор. Существует определенная связь между типом деревьев и геоэлектрическим разрезом подстилающей среды [1].
Лес рассматривается как изотропный полупроводящий
слой с относительной комплексной диэлектрической проницаемостью ![]() , высотой
, высотой ![]() ,
расстоянием между деревьями
,
расстоянием между деревьями ![]() , расположенный на
слоистой земле (l - длина волны в воздухе). Для определения
электрических параметров «леса-слоя» использовано соотношение для вертикально
поляризованной плоской волны в лесу [1, 2]:
, расположенный на
слоистой земле (l - длина волны в воздухе). Для определения
электрических параметров «леса-слоя» использовано соотношение для вертикально
поляризованной плоской волны в лесу [1, 2]:
![]() ,
,
справедливое в волновой зоне, где ![]() – вертикальная электрическая компонента
поля в лесу,
– вертикальная электрическая компонента
поля в лесу, ![]() – горизонтальная магнитная компонента
поля, Z0
–характеристический импеданс вакуума. Измерения эффективных
электрических параметров лесной растительности проведены в хвойных и лиственных
лесах различной густоты в диапазоне 50—620 кГц [1-3]. По результатам измерений
эффективная проводимость sл
хвойных лесов изменяется в пределах (0,12—0,3)×10-4
см/м, относительная диэлектрическая
проницаемость eл в пределах 1,2-1,4, в
среднем sл
= 0,2×10-4
см/м, eл
=1,3. Для лиственных лесов: sл =
(1,0 - 0,67)×10-4 Cм/м; eл
=
2—2,9. в среднем sл =
0,6×10-4
см/м, eл
= 2,7. Для однотипных пород деревьев значения sл
и eл
леса зависят от густоты лесной растительности - чем гуще лес, тем выше значения
sл
и eл.
В целом как проводимость, так и диэлектрическая проницаемость хвойных лесов
ниже, чем у лиственных лесов и кустарников. По-видимому, объяснить это можно
тем, что объем зеленой массы и ее электрические параметры в трехкомпонентной
смеси «воздух-древесина-листва» у лиственных пород больше, чем у хвойных. По
данным измерений, полученных мостовым методом (мост Е-10-2) в диапазоне
400—1000 кГц, для листьев березы e = 44—52, s
= 0,6—0,9 мСм/м; для сосновой хвои e = 7—9, s
= 0,1 мСм/м; для травы e = 33—44, s = 0,8—1,2
мСм/м. Следует отметить, что в работе [4] получен другой результат. Показано,
что эффективные значения комплексной диэлектрической проницаемости «леса-слоя»
– горизонтальная магнитная компонента
поля, Z0
–характеристический импеданс вакуума. Измерения эффективных
электрических параметров лесной растительности проведены в хвойных и лиственных
лесах различной густоты в диапазоне 50—620 кГц [1-3]. По результатам измерений
эффективная проводимость sл
хвойных лесов изменяется в пределах (0,12—0,3)×10-4
см/м, относительная диэлектрическая
проницаемость eл в пределах 1,2-1,4, в
среднем sл
= 0,2×10-4
см/м, eл
=1,3. Для лиственных лесов: sл =
(1,0 - 0,67)×10-4 Cм/м; eл
=
2—2,9. в среднем sл =
0,6×10-4
см/м, eл
= 2,7. Для однотипных пород деревьев значения sл
и eл
леса зависят от густоты лесной растительности - чем гуще лес, тем выше значения
sл
и eл.
В целом как проводимость, так и диэлектрическая проницаемость хвойных лесов
ниже, чем у лиственных лесов и кустарников. По-видимому, объяснить это можно
тем, что объем зеленой массы и ее электрические параметры в трехкомпонентной
смеси «воздух-древесина-листва» у лиственных пород больше, чем у хвойных. По
данным измерений, полученных мостовым методом (мост Е-10-2) в диапазоне
400—1000 кГц, для листьев березы e = 44—52, s
= 0,6—0,9 мСм/м; для сосновой хвои e = 7—9, s
= 0,1 мСм/м; для травы e = 33—44, s = 0,8—1,2
мСм/м. Следует отметить, что в работе [4] получен другой результат. Показано,
что эффективные значения комплексной диэлектрической проницаемости «леса-слоя» ![]() не зависят от породы деревьев: хвойные
или лиственные, от возраста лесных массивов, т.е. их высоты, диаметра стволов и
крон деревьев, а также от густоты лесных массивов. По данным же наших измерений
такая зависимость существует. Полученные нами значения sл
и eл
использованы для учета слоя леса при расчетах распространения радиоволн по
картам геоэлектрических разрезов (ГЭР), а также для оценки влияния сезонных
изменений электрофизических параметров sл
и eл
лесной среды на трассах распространения радиоволн.
не зависят от породы деревьев: хвойные
или лиственные, от возраста лесных массивов, т.е. их высоты, диаметра стволов и
крон деревьев, а также от густоты лесных массивов. По данным же наших измерений
такая зависимость существует. Полученные нами значения sл
и eл
использованы для учета слоя леса при расчетах распространения радиоволн по
картам геоэлектрических разрезов (ГЭР), а также для оценки влияния сезонных
изменений электрофизических параметров sл
и eл
лесной среды на трассах распространения радиоволн.
2. Поверхностный импеданс структуры «лес-почва»
Рассмотрим
поверхностный импеданс d слоистой
среды «лес-почва» для типичных электрических свойств и высоты леса. В СДВ-ДВ
диапазонах слой леса высотой 7-25 м можно считать тонким [1,10]. Рассмотрим
двухслойную модельную среду «смешанный лес-почва» с типичными параметрами для
смешанного леса sл =
10-4 см/м, eл
=1,6.
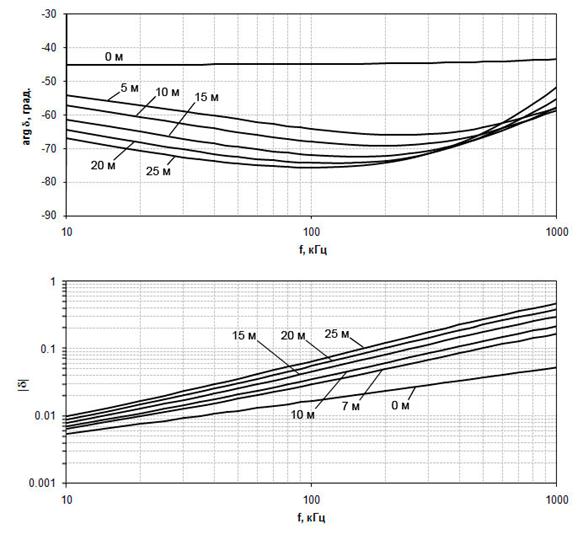
Для влажной почвы примем e = 20, s = 20 мСм/м [9]. На рис.1 представлена частотная зависимость
поверхностного импеданса d в диапазоне 10-1000 кГц для высоты леса от 7 до 25 м. Расчеты показывают, что слой леса с принятыми значениями sл
и eл
существенно
изменяет величину поверхностного импеданса слоистой среды «лес-почва»:
увеличивает модуль импеданса и смещает фазу в сторону сильно-индуктивных
импедансов (до -77°). Увеличение |d|
достигает 7,4 раза, а смещение ![]() доходит до 32°.
Изменение электрических параметров слоя леса в пределах значений sл
=
(0,2—1,2)×10-4 см/м и eл =
1,2—2 слабо влияет на величину импеданса d, тогда как увеличение
высоты леса h от 7 до 25 м почти линейно увеличивает |d|
и смещает jd в сильно-индуктивную
область. При этом на частотах от 500 до 1000 кГц для
высоты леса 20 и 25 м еще удовлетворяются импедансные граничные условия |d|2 << 1. При
рассмотрении зависимостей Re d(hл), Im d(hл)
установлено, что при увеличении высоты леса Re d остается почти
постоянной, а Im d изменяется линейно. Так как sп
>>
sл,
то справедливо соотношение [1]:
доходит до 32°.
Изменение электрических параметров слоя леса в пределах значений sл
=
(0,2—1,2)×10-4 см/м и eл =
1,2—2 слабо влияет на величину импеданса d, тогда как увеличение
высоты леса h от 7 до 25 м почти линейно увеличивает |d|
и смещает jd в сильно-индуктивную
область. При этом на частотах от 500 до 1000 кГц для
высоты леса 20 и 25 м еще удовлетворяются импедансные граничные условия |d|2 << 1. При
рассмотрении зависимостей Re d(hл), Im d(hл)
установлено, что при увеличении высоты леса Re d остается почти
постоянной, а Im d изменяется линейно. Так как sп
>>
sл,
то справедливо соотношение [1]:
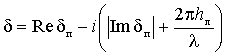 ,
,
согласно которому и происходит изменение d(hл). Следовательно, при прогнозировании распространения радиоволн над лесистыми трассами необходимо наиболее точно определить эффективную высоту слоя леса. Таким образом, частотные зависимости импеданса структуры «лес-почва» показывают, что распространение радиоволн над лесистыми трассами имеет особенности, характерные для сильно-индуктивных радиотрасс. Поэтому лесные районы Евразии, Африки, Америки и Австралии интересны для теории и практики распространения радиоволн.
Рис.1.
Частотная зависимость поверхностного импеданса двухслойной структуры «лес-почва»
в
диапазоне 10-1000 кГц для высоты леса от 7 до 25 м.
3. Метод расчета поля земной волны над импедансными трассами
Механизм распространения земной волны, амплитудно-фазовая структура которой имеет относительно высокую стабильность, является одним из основных в задачах расчета дальности действия радиолиний в ДВ-СВ диапазонах [10-15]. Под прогнозированием (моделированием) электромагнитного поля обычно понимают вычисление его амплитудно-фазовой структуры в пространстве и во времени на основе данных о среде, над которой распространяются волны. Наиболее адекватной моделью подстилающей среды на лесистых трассах является горизонтально-слоистая структура «лес-почва» с частотно-независимыми (или зависимыми) электрическими параметрами в каждом слое. Эта модель хорошо соответствует реальной земной поверхности в равнинных районах, имеющей в основном горизонтальную стратификацию слоев. Более точной по сравнению с однородной импедансной моделью подстилающей среды является модель многокусочной импедансной радиотрассы, когда импеданс изменяется вдоль направления распространения радиоволн. Область, существенная для распространения земной волны, охватывает несколько первых зон Френеля в окрестности геодезической линии, соединяющей излучатель и приемник. Известны следующие основные методы расчета функции ослабления W поля земной волны: 1) ряд нормальных волн (ряд В.А. Фока) [10-13]; 2) формула Калинина-Фейнберга [12]; 3) интегральное уравнение Хаффорда [10]; 4) интегральное уравнение Фейнберга [12,14]. При расчетах в СДВ-ДВ диапазонах подстилающая среда должна удовлетворять импедансным граничным условиям Леонтовича, то есть должно выполняться условие |d|2 << 1.
Рассмотрим задачу о поле вертикального
электрического диполя над однородной сферической поверхностью Земли.
Вертикальная составляющая напряженности электрического поля Е на
расстоянии R от излучателя на сферической поверхности Земли
представлена в виде ![]() , где Е0 –
напряженность электрического поля диполя, расположенного на плоской бесконечно
проводящей поверхности, W – функция ослабления. Модуль |W|
учитывает дополнительное (по отношению к множителю 1/R) убывание
амплитуды поля с расстоянием, а аргумент W (дополнительная фаза jдоп) характеризует
отклонение фазы волны от линейности в пространстве. Передатчик и приемник
расположены на поверхности Земли. Зависимость поля от времени принята в виде функции
, где Е0 –
напряженность электрического поля диполя, расположенного на плоской бесконечно
проводящей поверхности, W – функция ослабления. Модуль |W|
учитывает дополнительное (по отношению к множителю 1/R) убывание
амплитуды поля с расстоянием, а аргумент W (дополнительная фаза jдоп) характеризует
отклонение фазы волны от линейности в пространстве. Передатчик и приемник
расположены на поверхности Земли. Зависимость поля от времени принята в виде функции ![]() . В
расчетах излучаемая мощность равна 1 кВт.
. В
расчетах излучаемая мощность равна 1 кВт.
Модуль вертикальной составляющей электрического поля |EB| связан с модулем функции ослабления |W| формулой:
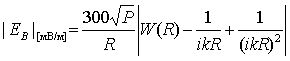 ,
,
где Р – излучаемая мощность, кВт; R – расстояние от источника до точки приема, км;
![]() –
индукционный,
–
индукционный, 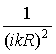 – статический члены, которые
«участвуют» в формировании поля в ближней зоне излучателя.
– статический члены, которые
«участвуют» в формировании поля в ближней зоне излучателя.
Расчет функции ослабления W для сферической земли проведен по ряду В.А. Фока [11]:
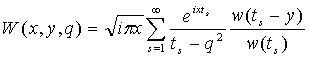 . (1)
. (1)
Здесь
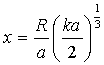 ,
,
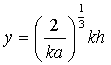 ,
,
 ,
,
где a – радиус Земли; d – приведенный поверхностный импеданс радиотрассы (-p/2 < arg d < p/2); h – высота приема сигнала над поверхностью Земли. Параметры ts являются корнями (нулями) трансцендентного уравнения:
w'(t)-qw(t)=0, (2)
где w(t) и w'(t) – функция Эйри, определяемая уравнением Эйри w¢¢(t)-tw(t)=0, и ее производная соответственно [11].
На начальном участке радиотрассы, где сферичностью Земли можно пренебречь, функция ослабления рассчитывается по формуле Зоммерфельда с помощью рядов [10] в предположении, что в окрестности излучателя справедлива модель однородной по импедансу плоской поверхности. В теории распространения радиоволн [10,13] показано, что поле над сильно-индуктивной трассой может на некоторых расстояниях превышать поле над бесконечно проводящей плоскостью, появляется ПЭВ. Интерференция между пространственной и поверхностной волнами вызывает также пространственные осцилляции поля.
4. Вычисление корней трансцендентного уравнения Фока
Основной особенностью при расчетах поля над сильно-индуктивными трассами по ряду В.А. Фока является вычисление корней ts трансцендентного уравнения Фока с учетом явления вырождения. Трансцендентное уравнение Фока вытекает из граничного условия Леонтовича для гладкой поверхности Земли. Рассмотрим динамику корней ts трансцендентного уравнения (2). Зависимость корней проанализируем при фиксированном значении аргумента q, а |q| будем менять от 0 до ∞. Корни t∞s и t0s, являющиеся абсолютными числами, удовлетворяют двум предельным случаям: q=∞ и q= 0 и лежат на луче arg t=p/3. Первые корни t∞s и t0s определяются таблично [11]: |t01|=1.019, |t02|=3.248, |t03|=4.82; |t∞1|=2.338, |t∞2|=4.088, |t∞3|=5.521. При s > 3 используются асимптотики: t0s=[(3p/2)(s-3/4)]2/3eip/3, t∞s=[(3p/2)(s-1/4)]2/3eip/3.
Для вычисления корней при малых значениях |q| (|q|<|t1/2|) удобно использовать дифференциальное уравнение для ts как функции от q:
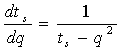 .
.
Для значений |q|>| t1/2| уравнение для ts будет иметь вид:
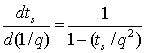 .
.
Используя данные формулы и вычисляя производные соответствующих порядков по q и (1/ q) , можно получить разложения в ряд Тейлора:
ts(q)=t0s+q/t0s-q2/(2t0s3)+….
ts(q)=t∞s+1/q+t∞s/(3q3)+….
При -90° <arg d < -60°
динамика корней характеристического уравнения на комплексной плоскости (t) усложняется. Сектор (-70,8° < arg d < -60°) является областью
возможного смыкания (вырождения) корней ts. Формула 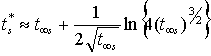 является
одним из приблизительных соотношений для корня вырождения
является
одним из приблизительных соотношений для корня вырождения ![]() [10]. При s®∞ фаза корня возможного вырождения arg
[10]. При s®∞ фаза корня возможного вырождения arg ![]() будет стремиться к 60°. При этом импедансы с фазой arg d = -70,8° соответствуют смыканию
первого и второго корней, импедансы с фазой arg d = -66,5° соответствуют смыканию
второго и третьего корней, и так далее. При arg d = -60° вырождаются корни
с бесконечно большими номерами. В этом случае в точках q= ±t1/2 происходит потеря аналитичности
функции ts(q). Для импедансов структуры «лес-почва», попадающих в
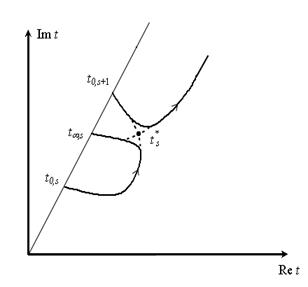
интервал -90° < arg d < -70,8° (0° < arg q < 19,2°), смыкания корней нет. На рис.
2а показан «предвырожденный» случай, когда arg q > arg qB.
Здесь текущая линия исходит из точки t0s и входит в точку t∞s, бесконечная ветвь выходит из точки t0s+1. Пунктирная линия показывает
траекторию нулей при вырождении, когда arg q = arg qB.
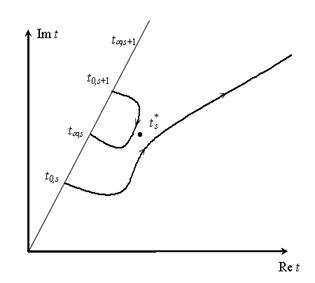
Рис.2б показывает «снятие» явления вырождения при arg q < arg qB,
здесь происходит «перекидывание» корней с высшего на низший, бесконечная ветвь
теперь выходит из точки t0s.
будет стремиться к 60°. При этом импедансы с фазой arg d = -70,8° соответствуют смыканию
первого и второго корней, импедансы с фазой arg d = -66,5° соответствуют смыканию
второго и третьего корней, и так далее. При arg d = -60° вырождаются корни
с бесконечно большими номерами. В этом случае в точках q= ±t1/2 происходит потеря аналитичности
функции ts(q). Для импедансов структуры «лес-почва», попадающих в
интервал -90° < arg d < -70,8° (0° < arg q < 19,2°), смыкания корней нет. На рис.
2а показан «предвырожденный» случай, когда arg q > arg qB.
Здесь текущая линия исходит из точки t0s и входит в точку t∞s, бесконечная ветвь выходит из точки t0s+1. Пунктирная линия показывает
траекторию нулей при вырождении, когда arg q = arg qB.
Рис.2б показывает «снятие» явления вырождения при arg q < arg qB,
здесь происходит «перекидывание» корней с высшего на низший, бесконечная ветвь
теперь выходит из точки t0s.
а) б)
Рис.2. Локализация линий нулей трансцендентного уравнения:
а)– предвырожденная ситуация, б)– послевырожденная ситуация.
Для радиотрассы с импедансом, лежащем в области -p/2 < arg d < -p/3, существует один член ряда под некоторым номером N, при котором при |q|®∞ кривая tN|argq=const®∞. Такие значения tN при |q| >>1 описываются асимптотикой: tN(q)||q|®∞= q2+1/(2q) [10].
Отметим, что при tN|argq=const®∞ N-й член ряда совпадает с поверхностной волной, которая выделяется в асимптотике решения задачи для плоской Земли с сильно-индуктивным поверхностным импедансом. После подстановки асимптотики в ряд Фока получаем:
![]() ,
, 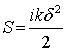 .
.
В этом случае N-й член ряда является функцией ослабления поверхностной волны над сферической Землей WПОВ. Сумма остальных членов ряда будет являться функцией ослабления пространственной волны WПР, а W=WПР+WПОВ. Фаза WПОВ растет быстрее фазы WПР, особенно при начальных значениях N и при тем больших значениях |q|, чем меньше значение arg q. Поэтому при |WПР|~|WПОВ| имеет место явление интерференции, которое вначале при малом отличии значений фаз обеих волн будет проявляться в виде сильного нарастания уровня результирующего поля. Затем при постепенном увеличении отличия значений фаз уровень поля будет снижаться. При достижении противофазы пространственной и поверхностной волн модуль функции ослабления может приблизиться к нулевому значению. После прохождения противофазы уровень поля вновь начинает расти. Таким образом, может иметь место немонотонное интерференционное убывание уровня поля при удалении от источника. В секторе -90° < arg d < -70,8° (0° < arg q < 19,2°) явление вырождения корней не происходит, на бесконечность уходит первая линия нулей ts. В этом случае затухание поверхностной волны оказывается наиболее близким к затуханию последующих волн, при этом первая нормальная волна является основной. Поэтому процесс интерференции здесь может выглядеть наиболее отчетливо.
5. Результаты расчетов распространения радиоволн над однородной импедансной радиотрассой «лес -почва» и их анализ
Рассмотрим расчеты функции ослабления
над импедансной трассой «лес-почва» в диапазоне 50 – 500 кГц. Из теории
распространения радиоволн над слоистыми средами [10,13] следует, что над
трассами с сильно-индуктивным импедансом появляется ПЭВ [15]. Эта волна,
экспоненциально затухающая по высоте, представляет практический интерес, так
как ее энергия убывает обратно пропорционально расстоянию от источника, в то
время как энергия пространственной (объемной) электромагнитной волны убывает
обратно пропорционально квадрату расстояния от источника. Функция ослабления W над сильно-индуктивной плоской
трассой содержит член ![]() , соответствующий поверхностной
волне. Максимум ПЭВ, равный
, соответствующий поверхностной
волне. Максимум ПЭВ, равный ![]() , наблюдается на
расстоянии
, наблюдается на
расстоянии 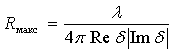 .
.
Сравнение численных данных для функции ослабления и уровня поля на однородной трассе «лес-почва» длиной 1000 км с поверхностным импедансом, соответствующим рис.1, показало, что условия распространения радиоволн над лесистыми трассами из-за сильно-индуктивного импеданса на расстояниях от излучателя, существенно зависящих от частоты, более благоприятны, чем над хорошо проводящей земной поверхностью (рис.3).
Проведем анализ пространственной зависимости |W| на разных частотах. Из графиков на рис.3 следует, что на частотах выше 50 кГц |W| имеет характерный для ПЭВ пространственный максимум |W|макс на расстояниях Rмакс. В табл.1 представлены расчетные значения |W|макс и Rмакс при изменении высоты леса от 7 до 25 м. Из табл.1 следует, что на частотах 50 – 300 кГц |W|макс увеличивается с ростом высоты леса. Однако при этом Rмакс увеличивается только на частотах 50 и 100 кГц. На частотах от 300 до 500 кГц Rмакс не превышает 33 км и резко уменьшается до 1 км на частоте 500 кГц при высоте леса 25 м. Физической причиной такого уменьшения Rмакс является рассмотренная в п.4 интерференция между пространственной и поверхностной волнами, которая вызывает пространственные осцилляции поля. Она сильно зависит от длины волны l и соотношения между высотой леса hл и l. Следовательно, наиболее благоприятными условия распространения радиоволн над лесистыми трассами будут в диапазоне частот от 50 до 150-200 кГц.
Таблица 1. Частотная зависимость значений |W|макс и расстояний Rмакс для ПЭВ при разной высоте леса
|
f, кГц
h, м |
50 |
100 |
200 |
300 |
400 |
500 |
||||||
|
|W|макс |
Rмакс, км |
|W|макс |
Rмакс, км |
|W|макс |
Rмакс,км |
|W|макс |
Rмакс,км |
|W|макс |
Rмакс,км |
|W|макс |
Rмакс,км |
|
|
7 |
1,03 |
26 |
1,104 |
75 |
1,242 |
71 |
1,277 |
33 |
1,262 |
17 |
1,228 |
8 |
|
10 |
1,054 |
59 |
1,178 |
108 |
1,376 |
78 |
1,401 |
29 |
1,342 |
13 |
1,288 |
6 |
|
15 |
1,099 |
101 |
1,33 |
100 |
1,565 |
67 |
1,511 |
22 |
1,417 |
9 |
1,33 |
4 |
|
20 |
1,154 |
139 |
1,5 |
175 |
1,676 |
52 |
1,559 |
15 |
1,426 |
6 |
1,333 |
2 |
|
25 |
1,223 |
181 |
1,61 |
203 |
1,739 |
39 |
1,556 |
9 |
1,398 |
4 |
1,327 |
1 |
В табл. 2 представлена пространственная область существования ПЭВ (|W| > 1) в зависимости от частоты и высоты леса. На частотах 50 и 100 кГц дальность действия радиолиний на ПЭВ достигает 600-800 км и увеличивается с ростом высоты леса. На частоте 200 кГц дальность действия радиолинии на ПЭВ при высоте леса 10 м достигает 288 км. На частотах от 300 до 500 кГц дальность действии радиолиний на ПЭВ существенно уменьшается при увеличении высоты леса. Этот диапазон частот характеризуется плохими условиями распространения радиоволн над лесистыми трассами. Однако этот эффект может быть использован при разработке методов дополнительного ослабления электромагнитных полей [7]. Полученные численные результаты следует учитывать при выборе рабочих частот ДВ-СВ радионавигационных систем, систем связи и радиовещания в лесистых районах. В табл.3 представлены расчеты модуля функции ослабления |W| и уровня поля Е на частоте 100 кГц на расстояниях 50, 100, 200, 300 и 400 км от источника в зависимости от высоты леса. Сравнение численных данных свидетельствует о том, что условия распространения радиоволн над лесными трассами из-за появления ПЭВ более благоприятны, чем над почвой.
Таблица 2. Пространственная область существования ПЭВ (|W|≥1) в зависимости от частоты и высоты леса
|
f, кГц h, м |
50 |
100 |
200 |
300 |
400 |
500 |
|
R,км |
R,км |
R,км |
R,км |
R,км |
R,км |
|
|
7 |
167 |
283 |
265 |
127 |
60 |
31 |
|
10 |
242 |
403 |
288 |
110 |
46 |
23 |
|
15 |
371 |
610 |
240 |
74 |
29 |
13 |
|
20 |
508 |
748 |
177 |
50 |
18,5 |
8,5 |
|
25 |
663 |
796 |
130 |
34 |
12 |
5 |
Так, на расстоянии 100 км уровень поля над почвой составляет Е = 2,82 мВ/м, а над структурой «лес – почва» с высотой леса 15 метров – Е = 3,92 мВ/м. Увеличение уровня поля составляет 39 %. На расстоянии 300 км это увеличение достигает уже 69%.
Таблица 3
|
R,км
hл, м |
50 |
100 |
200 |
300 |
400 |
|||||
|
0 7 10 15 20 25 |
|W| |
Е, мВ/м |
|W| |
Е, мВ/м |
|W| |
Е, мВ/м |
|W| |
Е, мВ/м |
|W| |
Е, мВ/м |
|
0,98 1,1 1,15 1,24 1,35 1,44 |
5,87 6,58 6,91 7,46 8,07 8,63 |
0,94 1,1 1,18 1,31 1,45 1,57 |
2,82 3,31 3,53 3,92 4,34 4,72 |
0,85 1,06 1,16 1,33 1,5 1,66 |
1,28 1,59 1,74 1,99 2,25 2,49 |
0,75 0,986 1,09 1,28 1,47 1,63 |
0,75 0,986 1,09 1,28 1,47 1,63 |
0,66 0,9 1,01 1,21 1,39 1,53 |
0,49 0,67 0,76 0,9 1,04 1,15 |
|
Анализ численных данных для модуля функции ослабления и уровня поля для однородной трассы «лес-почва» с поверхностным импедансом, соответствующим рис.1 и толщиной леса от 7 до 25 метров на расстояниях до 1000 км, показал, что при сильно-индуктивном импедансе условия распространения радиоволн над лесистыми трассами зависят от частоты и расстояния от излучателя. При |W| > 1, существенно зависящем в диапазоне 50-500 кГц от частоты, условия распространения при появлении ПЭВ более благоприятны, чем над однородной идеально проводящей поверхностью. Результаты моделирования показывают сильное влияние лесных массивов на распространение радиоволн СДВ-ДВ диапазонов.
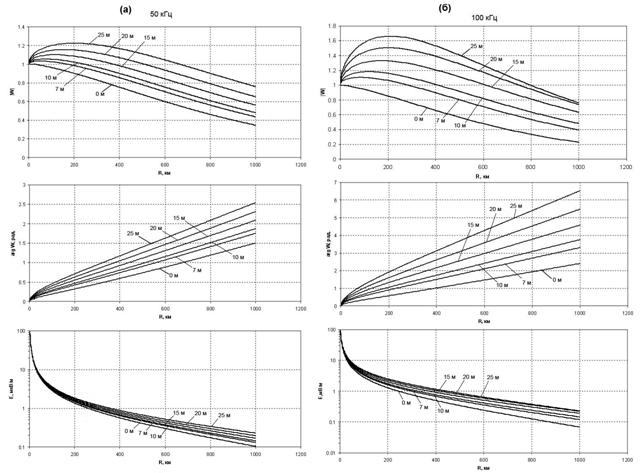
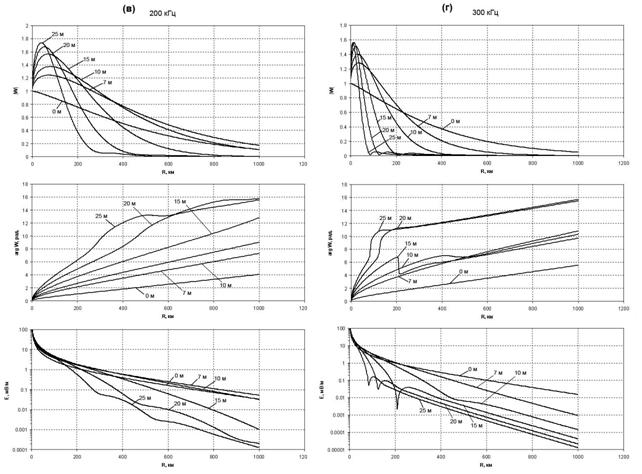
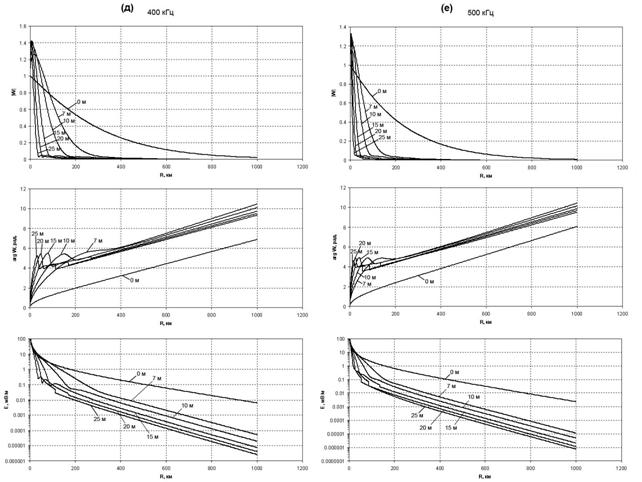
Рис. 3 а-е. Графики |W|, φдоп. и уровня
поля земной волны Е над радиотрассой «лес-почва»
на частотах
50(а),100(б), 200 (в), 300 (г), 400(д) и 500 (е) кГц.
6. Заключение
В диапазоне частот 50 -500 кГц на трассах длиной до 1000 км проведено численное моделирование электромагнитного поля для задачи распространения земной волны, создаваемой вертикальным электрическим диполем над слоистой структурой «лес-почва», имеющей сильно-индуктивный поверхностный импеданс. На основе разработанного комплекса программ моделирования показано, что в диапазоне 50-200 кГц условия распространения радиоволн над лесом всегда более благоприятны, чем над почвой без леса. Получены значения модуля функции ослабления |W|, превышающие единицу и достигающие |W| = 1,74, которые обусловлены поверхностной электромагнитной волной (ПЭВ). Аналитически рассмотрен процесс интерференции между пространственной и поверхностной волнами, который вызывает пространственные осцилляции поля. Анализ полученных фаз импедансов показал возможность значительного увеличения уровня ПЭВ в многослойных структурах «диэлектрик на проводнике». Подтверждение обнаруженного эффекта появления ПЭВ экспериментально получено при измерениях над двухслойной структурой «лес – грунт» [4] и «лед - соленая вода» [15]. Результаты экспериментов показали хорошее совпадение с данными численного моделирования. При анализе численных результатов для |W| и уровня поля E установлено, что условия распространения ДВ радиоволн над лесистыми трассами зависят от частоты, высоты леса и расстояния до излучателя. Численными расчетами показано сильное влияние лесных массивов на распространение радиоволн СДВ-СВ диапазонов. Результаты моделирования дали основание для проведения эксперимента в равнинных районах востока России. Рассмотрены и определены возможные районы эксперимента. Численные результаты могут быть использованы для выбора оптимальных рабочих частот ДВ-СВ радиолиний как средней, так и малой дальности.
Исследование выполнено за счет гранта Российского научного фонда (проект №14-19-01079) в Институте физического материаловедения СО РАН.
Литература
1. Башкуев Ю.Б. Электрические свойства природных слоистых сред. Новосибирск: Изд-во СО РАН, 1996, 207 с.
2. Башкуев Ю.Б., Адвокатов В.Р., Балханов В.К. Способ измерения эффективных электрических свойств лесной среды в длинноволновом диапазоне радиоволн и устройство для его осуществления // Патент на изобретение RU № 2336520 C1 G 01N 22/00, G 01R 27/00. Бюллетень № 29. 2008.
3. Балханов В.К., Адвокатов В.Р., Башкуев Ю.Б. Усредненные электрические характеристики «лесо-слоя» и высота лесного покрова // Журнал технической физики, 2014, Т. 84, № 8. с. 132-136.
4. Егоров В.А. Влияние растительного покрова на распространение средних и более длинных электромагнитных волн// Автореф. дисс. канд. физ.-мат. наук, Санкт-Петербург, 2007, 21 с.
5. Egorov V.A., Makarov G.I. «Influence of vegetable cover on propagation of electromagnetic waves with wavelength longer than 100 m» International Journal of Geomagnetism and Aeronomy. Vol.6, G13005, 2006.
6. Егоров В.А. , Макаров Г.И. Точность прогнозирования функции ослабления при помощи граничных условий импедансного типа в случае двухслойной трассы распространения // Радиотехника и электроника, 2011, Т. 56, №6, с. 694-697.
7. Tamir Th. «On radio-wave propagation in forest environments» IEEE Trans. Antennas and Propagation, vol. AP-15, №6, November 1967, p. 806-817.
8. Ломухин Ю.Л., Ветлужский А.Ю. Методы дополнительного ослабления электромагнитных полей. - Новосибирск: Наука, 2003, 136 с.
9. Башкуев Ю.Б., Хаптанов В.Б. Электрические характеристики черноземных почв Аларской степи // Вестник Бурятского государственного университета (серия Химия и физика), 2014, №3, с. 156-160.
10. Макаров Г.И., Новиков В.В., Рыбачек С.Т. Распространение электромагнитных волн над земной поверхностью. М.: Наука, 1991, 196 с.
11. Фок В.А. Проблемы дифракции и распространения электромагнитных волн. М.: Сов. Радио, 1970, 517 с.
12. Фейнберг Е.Л. Распространение радиоволн вдоль земной поверхности. М.: Физматлит, 1999, 496 с.
13. Wait J. R. Electromagnetic waves in stratified media. Pergamon Press, New York-Paris, 1962, 372 p.
14. Дембелов М.Г. Свидетельство об официальной регистрации программы для ЭВМ № 2007614416. Расчет функции ослабления поля земной волны над неоднородными радиотрассами по методу обобщенного интегрального уравнения Е.Л. Фейнберга. – М.: РОСПАТЕНТ, 18.10.2007.
15. Башкуев Ю.Б., Хаптанов В.Б., Дембелов М.Г. Экспериментальное доказательство существования поверхностной электромагнитной волны // Письма в Журнал технической физики, 2010, Т. 36, № 3. с. 88-95.