| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9 , 2000 |
ИСПОЛЬЗОВАНИЕ НЕКОГЕРЕНТНОГО ИЗЛУЧЕНИЯ ДЛЯ ТОМОГРАФИИ СРЕД С ПОГЛОЩЕНИЕМ
В. П. Якубов, Д.В. Лосев
Томский государственный университет
Получена 22 сентября 2000 г.
Рассматривается задача о томографии пространственно распределенного некогерентного источника излучения. Задача решается на основе обращения интегрального уравнения, сформулированного для углового распределения интенсивности, измеряемого на поверхности определенного радиуса. Предлагаемое обратное интегральное преобразование обобщает известные решения и учитывает ослабление, как за счет сферической расходимости, так и за счет экспоненциального ослабления.
1. Введение
В настоящее время методы
томографии признаются самыми
перспективными для целей интроскопии
неоднородных сред и диагностики
биологических тканей [1].
Получаемая с их помощью информация
отличается как объемом, так и точностью при
сохранении наглядности представления.
Область применения этих методов
чрезвычайно широка: от медицины до
геофизики и аэрономии. Постоянное
расширение области применения
томографических методов определяет
непрерывное совершенствование как самих
этих методов, так и способов зондирования
сред. Для зондирования сред начинают
использоваться более низкочастотные виды
электромагнитных полей (радиотомография [2,
3], импедансная томография [4],
магнитная томография [5]). Методы
обработки волновых проекций становятся
более тонкими, начинают учитываться
эффекты, которыми ранее пренебрегалось (дифракция,
рефракция, поглощение), а также их
комбинации. Сдерживающим здесь является
сложность рассматриваемых явлений и слабая
разработанность математических методов.
Что касается применения прямых численных
решений, то их устойчивость и точность
оставляет желать лучшего. Базовым методом математического
обеспечения современных томографов
является метод обратных проекций и его
модификации. Наиболее устойчивыми и
точными являются методы, основанные на
использовании различных интегральных
преобразований. Например, для
восстановления двумерных неоднородностей
при круговой схеме обзора эффективным
методом является разложение снятых теневых
проекций по круговым гармоникам в
сочетании с т.н. каузальным или
некаузальным решениями [6]. Однако
ядра этих преобразований обладают
особенностями в окрестности начала
координат, и это приводит к неустойчивости
решения. Для томографии распределения
некогерентных источников предложен метод
сведения задачи к интегральному уравнению
типа свертки и решения его с использованием
алгоритма быстрого преобразования Фурье [7].
Во всех этих случаях поглощением излучения
в среде приходится пренебрегать или
считать его исчезающе малым, иначе задача
просто не решается. Неучет этого влияния (особенно,
при использовании слабого по интенсивности
излучения или сильного поглощения в среде)
может приводить к значительным
погрешностям восстановления томограмм.
Несмотря на актуальность этой задачи, как
отмечается в обзоре [8], методов,
учитывающих фоновое поглощение излучения в
произвольной неоднородной среде, вплоть до
последнего времени в мире не разработано.
Исключение составляет малоинтересный
случай осесимметричных сред. В настоящей
работе предлагается математическое
решение общей задачи. Рассмотрим задачу о
пространственном распределении плотности
интенсивности источника излучения Рис. 1. Геометрия задачи.![]() в предположении его некогерентности и
локализации внутри объема
в предположении его некогерентности и
локализации внутри объема ![]() ,
ограниченного сферой радиуса
,
ограниченного сферой радиуса ![]() (рис.1). На границе этой сферы
наблюдаемая интегральная интенсивность
некогерентного излучения описывается
выражением [9]:
(рис.1). На границе этой сферы
наблюдаемая интегральная интенсивность
некогерентного излучения описывается
выражением [9]:
Здесь ![]() - коэффициент линейного поглощения по
интенсивности для фоновой среды в которой
распространяется поле излучения. Как видно
из (1), при этом наряду с фоновым поглощением
учитывается ослабление излучения за счет
сферической расходимости.
- коэффициент линейного поглощения по
интенсивности для фоновой среды в которой
распространяется поле излучения. Как видно
из (1), при этом наряду с фоновым поглощением
учитывается ослабление излучения за счет
сферической расходимости.
|
(2) |
где интегрирование ведется вдоль прямой, проведенной из точки наблюдения
Заметим, что радиус вектор
Для дальнейшего анализа удобно
перейти в интеграле (2) к
интегрированию по полярной переменной ![]() ,
предварительно представив распределение
интенсивности источника излучения
,
предварительно представив распределение
интенсивности источника излучения
|
(3) |
В результате интеграл (2) представляется в виде разложения:
|
(4) |
где
|
(5) |
Соотношения (3) - (5) представляют собой решение прямой задачи многоракурсного сканирования распределенного источника излучения
3. Решение задачи томографии в условиях поглощения
Уравнение (5)
является уравнением, обобщающим два
известных частных случая. Во-первых, это
случай отсутствия фонового затухания в
среде ![]() ,
но произвольного распределения
,
но произвольного распределения ![]() .
Для этого случая известны четыре решения:
каузальное, некаузальное [6], с
использованием обратного интегрального
преобразования Меллина [1] и
.
Для этого случая известны четыре решения:
каузальное, некаузальное [6], с
использованием обратного интегрального
преобразования Меллина [1] и
с использованием преобразования к уравнению в свертках [7]. Укажем здесь лишь каузальное решение:
|
(6) |
Во-вторых, это случай осевой симметрии (
|
(7) |
Предлагаемое нами общее решение уравнения (5) имеет вид:
|
(8) |
Очевидно, что выражение (8) содержит в себе как частные случаи и решение (6) при
Для доказательства справедливости решения (8) подставим его в исходное уравнение (5), которое при этом должно превратиться в тождество. Меняя порядок интегрирования, получаем, что
|
(9) |
где для внутреннего интеграла введено обозначение:
|
(10) |
В приложении будет показано, этот интеграл тождественно (при любых входящих в него параметрах!) равен
|
|
Это равенство становится тождеством, если выполняется условие
Восстановление
томограммы по многоракусным измерениям
интенсивности излучения ![]() сводится к нахождению коэффициентов
разложения
сводится к нахождению коэффициентов
разложения
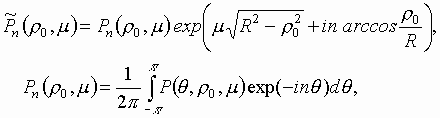
и последовательному выполнению интегрального преобразования (8) и суммирования (3).
4. Заключение
Таким образом, было показано, что
задача томографии может быть решена не
только в классическом случае непоглощающей
среды, чему соответствуют различные методы
обращения преобразования Радона, но и в
случае учета произвольного постоянного
поглощения в среде. Это дает возможность
повышения точности известных методов и
расширения сферы применения
томографических методов на новые области
науки и техники. Работа выполнена по грантам
Минобразования и РФФИ № 01-02-16546.
Литература
Приложение
Для доказательства тождества
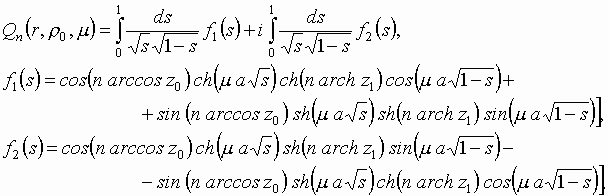
где:
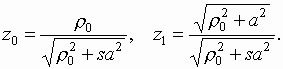 Интегралы такого типа вычисляются как
вычет в бесконечно удаленной точке [11]:
Интегралы такого типа вычисляются как
вычет в бесконечно удаленной точке [11]:
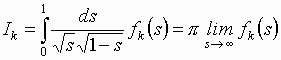 ,
,
![]() .
.
Интеграл для мнимой части элементарно вычисляется, если переписать
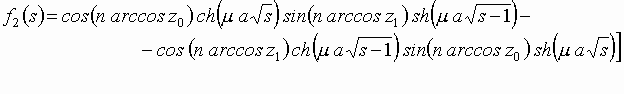
Очевидно, что при
 ,
и
,
и Для нахождения значения оставшегося интеграла с помощью простых тригонометрических преобразований перепишем функцию
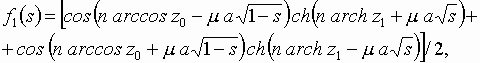
и найдем ее производную по переменной
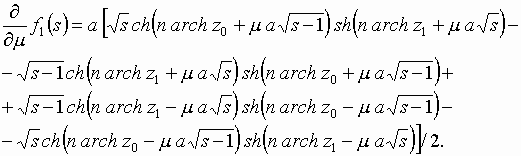
С учетом этого очевидно, что
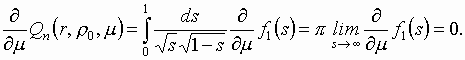
Отсюда можно записать, что
![]() ,
,
но при ![]() доказываемое тождество прямо вытекает из
каузального решения. Таким образом
тождество
доказываемое тождество прямо вытекает из
каузального решения. Таким образом
тождество ![]() доказано в случае наличия поглощения.
доказано в случае наличия поглощения.
Авторы:
Якубов Владимир Петрович, е-mail: yvlp@ic.tsu.ru;
Лосев Дмитрий Витальевич,
Томский государственный
университет