|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2002 |
|
Решение задачи развертки фазы и устранения неоднозначности определения высоты в двухчастотном интерферометре с синтезированием апертуры.
Ксендзук А.В.
Национальный аэрокосмический университет им. Н.Е. Жуковского «ХАИ».
Получена 18 сентября 2002 г.
В статье рассмотрен способ решения фазовой неоднозначности и развертки фазы в двухчастотном интерферометре с синтезированием апертуры антенны. Получена оригинальная структурная схема для двухчастотного интерферометра, позволяющая путем использования перемножителя эффективно решать задачи развертки фазы и устранения неоднозначности в определении высоты. Приведены результаты моделирования, подтверждающие теоретические выводы.
Независимо от вида обработки входного сигнала (метода оценки разности фаз сигналов в различных антеннах интерферометра) выходным параметром является гармоническая функция абсолютной фазы, [1] [2]:
где ![]() - волновое число,
- волновое число,
![]() - база интерферометра,
- база интерферометра,
![]() - средняя высота рельефа,
- средняя высота рельефа,
![]() - высота рельефа,
- высота рельефа,
![]() - расстояние от
середины базы интерферометра до точки пространства
- расстояние от
середины базы интерферометра до точки пространства ![]() .
.
При этом связь
между значением абсолютной фазы и ее оценкой ![]() задается неоднозначной функцией. В случае
отсутствия скачков высоты рельефа необходима развертка фазы, так как ее
оценочное значение изменяется в пределах от 0 до p.
Если же в области обзора присутствуют резкие скачки высоты, такие, что
изменение абсолютной фазы соответствует целому числу интервалов однозначности,
необходимо решение задачи неоднозначной оценки абсолютной фазы и,
соответственно, высоты.
задается неоднозначной функцией. В случае
отсутствия скачков высоты рельефа необходима развертка фазы, так как ее
оценочное значение изменяется в пределах от 0 до p.
Если же в области обзора присутствуют резкие скачки высоты, такие, что
изменение абсолютной фазы соответствует целому числу интервалов однозначности,
необходимо решение задачи неоднозначной оценки абсолютной фазы и,
соответственно, высоты.
Разделим ошибки оценки абсолютной фазы на нормальные и аномальные.
Нормальные ошибки возникают
вследствие присутствия аддитивного шума на входе измерительной системы.
Теоретически предельная точность измерений разности фаз ![]() в интерферометрической системе
при оптимальной обработке определяется с помощью дисперсии ошибок, [3]:
в интерферометрической системе
при оптимальной обработке определяется с помощью дисперсии ошибок, [3]:
где ![]() - энергетическое
соотношение сигнал/помеха,
- энергетическое
соотношение сигнал/помеха,
![]() - база интерферометра,
- база интерферометра,
![]() - длина волны
интерферометра.
- длина волны
интерферометра.
Очевидно, что чем больше отношение базы интерферометра к длине волны, тем меньше дисперсия ошибок оценки разности фаз в антеннах и, соответственно, меньше нормальные ошибки оценки высоты рельефа.
Однако при этом необходимо учесть, что связь между абсолютной фазой функции (и, соответственно, высотой рельефа поверхности) и ее оценкой задается неоднозначной функцией. Это может явиться причиной появления аномальных ошибок оценки абсолютной фазы и, соответственно, высоты рельефа. Этот факт можно записать следующим образом:
![]() ,
,
где ![]() - произвольное целое
число,
- произвольное целое
число,
Таким образом, в
интерферометрической системе помимо задачи оптимальной оценки разности фаз
сигналов в различных антеннах необходимо решать задачи развертки фазы и
устранения неоднозначности измерений. Решение задачи однозначной оценки фазы
можно интерпретировать как задачу оценки числа ![]() в последнем выражении. При решении этих
задач с точностью до нормальных ошибок и аппаратных погрешностей будет
восстановлена абсолютная фазы
в последнем выражении. При решении этих
задач с точностью до нормальных ошибок и аппаратных погрешностей будет
восстановлена абсолютная фазы ![]() и, соответственно, высота рельефа
и, соответственно, высота рельефа ![]() .
.
Задача развертки фазы не может быть точно решена в случае резких скачков высоты рельефа (на величину большую интервала однозначного определения). Интервал однозначного измерения фазы зависит от параметров интерферометрической системы, в частности, от рабочей частоты и базы. Таким образом, изменяя базу либо несущую частоту можно получить однозначные оценки высоты (без аномальных ошибок).
Однако при этом необходимо отметить, что при увеличении интервала однозначного определения абсолютной фазы и, соответственно, высоты рельефа ухудшается точность оценок разности фаз в интерферометрической системе. Таким образом, интервал однозначного определения и точность восстановления высоты рельефа находятся в противоречии, решить которое в одночастотном однобазовом интерферометре при отсутствии априорной информации не удается. Решение задачи однозначного восстановления высоты при одновременной высокой точности измерения можно получить при использовании многочастотных и/или многобазовых интерферометрических систем.
С точки зрения решения задачи устранения фазовой неоднозначности использование как многочастотных, так и многобазовых интерферометров эквивалентно. В общем случае развертывание многобазового интерферометра существенно сложнее, чем использование многочастотной системы. По этой причине вначале рассмотрим решение задачи однозначного определения высоты рельефа именно с помощью многочастотных интерферометрических систем.
Будем полагать, что при одной
базе ![]() имеется
набор несущих частот
имеется
набор несущих частот ![]() .
Тогда оценочное значение высоты при использовании частоты
.
Тогда оценочное значение высоты при использовании частоты ![]() определяется выражением:
определяется выражением:
Для исключения неоднозначности необходимо чтобы изменение аргумента находилось в пределах от 0 до p:
![]() ,
,
![]() ,
,
![]() .
.
Из последнего выражения видно,
что интервал однозначного измерения высоты определяется, в частности, несущей
частотой ![]() . При
ее увеличении интервал однозначного измерения
. При
ее увеличении интервал однозначного измерения ![]() и
и ![]() уменьшается, а при уменьшении - увеличивается.
уменьшается, а при уменьшении - увеличивается.
Выбор наименьшей несущей частоты ![]() необходимо осуществить
таким образом, чтобы интервал всех возможных изменений
необходимо осуществить
таким образом, чтобы интервал всех возможных изменений ![]() не превышал интервала однозначности
на этой частоте. После этого выполняется последовательное повышение точности
измерений при увеличении несущей частоты. Очевидно, что для того чтобы сохранялась
однозначность отсчета при переходе с измерений на одной частоте на другую,
требуется выполнение условия:
не превышал интервала однозначности
на этой частоте. После этого выполняется последовательное повышение точности
измерений при увеличении несущей частоты. Очевидно, что для того чтобы сохранялась
однозначность отсчета при переходе с измерений на одной частоте на другую,
требуется выполнение условия:
где ![]() - интервал
неоднозначности на несущей частоте
- интервал
неоднозначности на несущей частоте ![]() ,
,
![]() - ошибка оценки фазы на
несущей частоте
- ошибка оценки фазы на
несущей частоте ![]() (сумма
нормальной ошибки оценки разности фаз и аппаратурной ошибки).
(сумма
нормальной ошибки оценки разности фаз и аппаратурной ошибки).
Таким образом, зная величины ![]() путем использования
выражения (4) можно так подобрать несущие частоты интерферометрической системы,
чтобы получить заданную точность и при этом избежать неоднозначности в
определении высоты рельефа.
путем использования
выражения (4) можно так подобрать несущие частоты интерферометрической системы,
чтобы получить заданную точность и при этом избежать неоднозначности в
определении высоты рельефа.
Решение задачи развертки фазы при
наличии многочастотных наблюдений может быть получено с учетом того, что
изменение характера поведения высоты рельефа (и, соответственно характер изменения
второй производной неразвернутой абсолютной фазы) одинаково на всех частотах ![]() . Те точки пространства,
где происходит изменение знака второй производной
. Те точки пространства,
где происходит изменение знака второй производной ![]() можно определить путем использования
выражения:
можно определить путем использования
выражения:
где ![]() - оператор логического
умножения (оператор «И»).
- оператор логического
умножения (оператор «И»).
Развертка фазы при использовании
последнего выражения обычно дает более хорошие результаты, чем способ,
предложенный для однобазового одночастотного интерферометра. Причем
достоверность определения точек ![]() тем выше, чем больше различных частотных
каналов в интерферометре.
тем выше, чем больше различных частотных
каналов в интерферометре.
Рассмотрим решение задач развертки фазы для двухчастотного интерферометра. Выражения для оценок неразвернутой фазы запишем так:
где величины ![]() определяются значениями
несущих частот
определяются значениями
несущих частот ![]() .
.
Результаты
моделирования для двухчастотного интерферометра (соотношение частот выбрано
произвольно - ![]() )
показаны на рис. 1-5.
)
показаны на рис. 1-5.
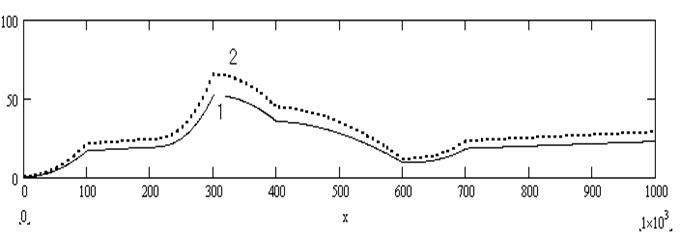
Рис. 1. Поведение высоты
рельефа ![]() .
.
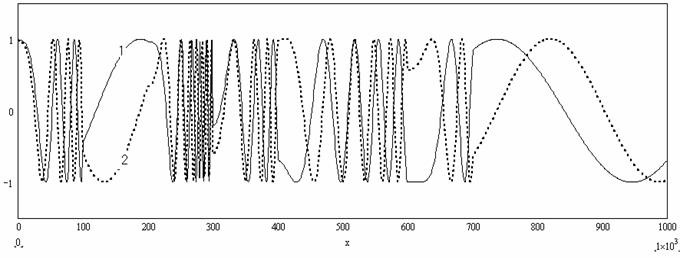
Рис.2. Поведение
абсолютной фазы. 1- на первой несущей частоте ![]() , 2- на второй несущей частоте
, 2- на второй несущей частоте ![]() .
.
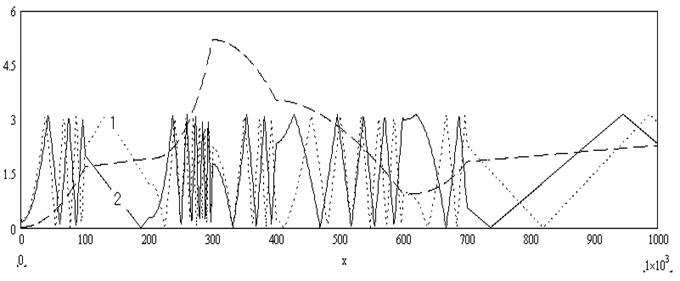
Рис.3. Поведение
функции 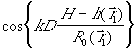 . 1-
на первой несущей частоте
. 1-
на первой несущей частоте 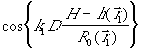 , 2- на второй несущей частоте
, 2- на второй несущей частоте 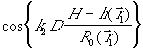 .
.
Как видно из рис.3. характер
поведения различен вследствие различия несущих частот ![]() и
и ![]() . Та же ситуация наблюдается и для
производных пространственной функции
. Та же ситуация наблюдается и для
производных пространственной функции  .
.
Рис.4.
Поведение производной косинуса абсолютной фазы. 1- на первой несущей частоте, 2- на второй несущей частоте.
Рис.5. Поведение неразвернутой абсолютной фазы на разных несущих частотах. 1- на первой несущей частоте, 2- на второй несущей частоте.
Различие в характере поведения неразвернутой фазы на различных несущих частотах позволяет определить точки пространства в которых изменяется поведение высоты рельефа (от монотонного возрастания до монотонного убывания) путем использования логического соотношения:
Это выражение представляет собой
модификацию (5) для случая двухчастотного интерферометра. Из последнего
выражения видно, что можно использовать как сами функции так и их
преобразования, инвариантные относительно точки изменения знака производной
пространственной функции  . Для наглядности в качестве такого
преобразования выбрана знаковая функция
. Для наглядности в качестве такого
преобразования выбрана знаковая функция ![]() . При аппаратной реализации предложенного
алгоритма это позволит использовать относительно простые битовые вычислительные
устройства при определении точек изменения характера поведения рельефа поверхности.
. При аппаратной реализации предложенного
алгоритма это позволит использовать относительно простые битовые вычислительные
устройства при определении точек изменения характера поведения рельефа поверхности.
Рис. 6.
Работа алгоритма выделения
точек изменения характера поведения рельефа. 1- знак функции  , 2- знак
, 2- знак 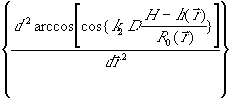 , 3- результат
развертки фазы.
, 3- результат
развертки фазы.
Таким образом, по результатам моделирования можно отметить, что применение двухчастотных измерений позволяет корректно провести развертку фазы. Интервал неоднозначного определения высоты определяется наименьшей несущей частотой. При проектировании двухчастотного интерферометра несущие частоты надо выбирать таким образом, чтобы выполнялось соотношение (7).
Однако наличие всего двух несущих частот обычно не позволяет при требуемой точности определения высоты рельефа добиться большого интервала однозначности измерений. То есть предпочтительно использовать больше двух несущих частот (многочастотную интерферометрическую систему). Однако необходимо отметить, что применение многочастотных интерферометров требует наличия дорогостоящих высокостабильных генераторов.
Для того чтобы сохранить достоинства многочастотных интерферометров и устранить недостатки рекомендуется воспользоваться перемножителем после схемы оптимального приема по двум несущим частотам. Структурная схема такого интерферометра показана ниже на рис. 7.
Рис.7. Структурная схема двухчастотного интерферометра с перемножителем.
Принцип
действия предложенного двухчастотного интерферометра основывается на том, что
на выходе этого перемножителя формируются гармоники с частотами, определяемыми
соотношением ![]() где
где
![]() -
произвольные целые числа. Входные сигналы по двум несущим
-
произвольные целые числа. Входные сигналы по двум несущим ![]() и
и ![]() поступают на приемные устройства и перемножитель.
После этого фильтрами Фi выделяются требуемые гармоники
с частотами
поступают на приемные устройства и перемножитель.
После этого фильтрами Фi выделяются требуемые гармоники
с частотами ![]() .
Полученные сигналы используются для развертки фазы и устранения
неоднозначности.
.
Полученные сигналы используются для развертки фазы и устранения
неоднозначности.
Теоретически, путем использования гармоник можно достичь как высокой точности оценки высоты рельефа поверхности, так и избежать аномальных ошибок связанных с неоднозначным определением фазы.
Однако необходимо учитывать
уменьшение амплитуды гармоники после перемножителя с увеличением числа ![]() . Вследствие этого
уменьшается амплитуда полезного сигнала на
. Вследствие этого
уменьшается амплитуда полезного сигнала на ![]() -й гармонике, уменьшается отношение сигнал/помеха
и, соответственно, возрастают нормальные ошибки измерения фазы. Более того, в
частотную полосу
-й гармонике, уменьшается отношение сигнал/помеха
и, соответственно, возрастают нормальные ошибки измерения фазы. Более того, в
частотную полосу ![]() -го
фильтра могут попадать гармоники более высоких порядков. То есть будут
дополнительные помехи при оценке фазы сигнала, что необходимо учитывать при
выборе несущих частот
-го
фильтра могут попадать гармоники более высоких порядков. То есть будут
дополнительные помехи при оценке фазы сигнала, что необходимо учитывать при
выборе несущих частот ![]() и
и
![]() , параметров
фильтров Фi.
, параметров
фильтров Фi.
Таким образом, по результатам моделирования можно сказать, что предложенная структурная схема двухчастотного интерферометра позволяет эффективно решать задачи восстановления высоты и развертки фазы.
Список литературы.
1. Радиолокационные методы исследования земли под ред. Ю.А. Мельника, - Москва: 1980.
2. X-SAR Interferometry, Dieter Just. СD SIR/X-SAR, Deutsche Agentur for Raumfahrtangelegenheiten (DARA) GmbH
3. Фалькович С.Е., Хомяков Э.Н. статистическая теория измерительных ралиосистем.-М.:Радио и связь, 1981.
 (1)
(1) , (2)
, (2)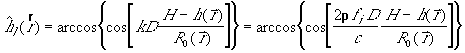
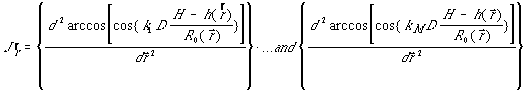 . (5)
. (5)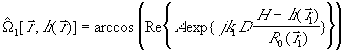 , (6)
, (6)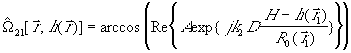 . (7)
. (7)

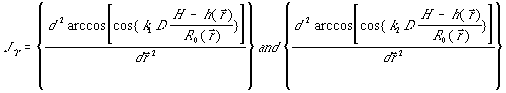 .(8)
.(8)