ОБНАРУЖЕНИЕ СИГНАЛОВ С НЕИЗВЕСТНЫМИ НАЧАЛЬНЫМИ ФАЗАМИ
М. А. Киреев
Филиал “Московского центра автоматизированного управления воздушным движением” Федеральное государственное унитарное предприятие “Госкорпорация по ОрВД”, Москва
Получена 13 сентября 2011 г.
Аннотация. В статье решается задача синтеза эффективного алгоритма приема полезного сигнала с неизвестными начальными фазами на фоне негауссовых помех. Показано, что для эффективного обнаружения сложного сигнала приемник должен в своем функциональном составе содержать нелинейный блок. Получены рабочие характеристики приемника обнаружения полезного сигнала на фоне негауссовых помех.
Ключевые слова: радиотехническая система, негауссова помеха, аддитивная смесь, оптимальный приемник, аналитическая функция, пороговый уровень.
Abstract. The problem of synthesis of effective algorithm of reception of a useful signal with unknown initial phases against ungauss hindrances is considered in the article. It is shown that for effective detection of a difficult signal the receiver should contain the nonlinear block in the functional structure. Performance data of the receiver of detection of a useful signal against ungauss hindrances are received.
Keywords: radio engineering system, ungauss hindrance, an additive mix, the optimum receiver, analytical function, threshold level.
Прием радионавигационных и радиосвязных сигналов сопровождается случайными аддитивными помехами и мешающими сигналами, имеющими зачастую негауссово распределение. Помимо этого, параметры принимаемых сигналов флуктуируют. При отражении радиоволн от морской поверхности или суши флуктуации вызываются изменением свойств отражающей поверхности. Флуктуации параметров радиосигналов происходят также при их прохождении через турбулентную атмосферу, коэффициенты преломления и поглощения в которой на различных высотах меняются по случайным законам [1]. По этой причине при приеме и обработке навигационной и связной информации используются методы теории вероятности и математической статистики, а сами прием и обнаружение рассматриваются как математическая задача.
Предположим необходимо осуществить обнаружение
полезного сложного сигнала с неизвестной начальной фазой ![]() :
:
где ![]() - амплитуды элементарных сигналов;
- амплитуды элементарных сигналов; ![]() - функции угловой
модуляции;
- функции угловой
модуляции; ![]() -
начальные фазы сигналов. На полезный сигнал
-
начальные фазы сигналов. На полезный сигнал ![]() действует аддитивная негауссова
помеха
действует аддитивная негауссова
помеха ![]() :
:
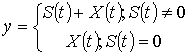 .
(2)
.
(2)
Для негауссовой помехи ![]() типа белого шума функционал
вероятности
типа белого шума функционал
вероятности ![]() , как
показано в [2], равен:
, как
показано в [2], равен:
 , (3)
, (3)
где ![]() - одномерная плотность
вероятности негауссовой помехи
- одномерная плотность
вероятности негауссовой помехи ![]() ,
, ![]() - интервал наблюдения равный
длительности сигнала. Алгоритм обнаружения в оптимальном приемнике, рис.1,
с учетом (2,3) равен:
- интервал наблюдения равный
длительности сигнала. Алгоритм обнаружения в оптимальном приемнике, рис.1,
с учетом (2,3) равен:
где ![]() есть случайный процесс на
выходе нелинейного четырехполюсника (НЧП), амплитудная характеристика
которого равна:
есть случайный процесс на
выходе нелинейного четырехполюсника (НЧП), амплитудная характеристика
которого равна:
Кроме НЧП в состав оптимального приемника
входит коррелятор или оптимальный линейный фильтра (ОФ),
частотная характеристика которого сопряжена со спектром сигнала ![]() , и порогового
устройства (ПУ), рис.1.
, и порогового
устройства (ПУ), рис.1.
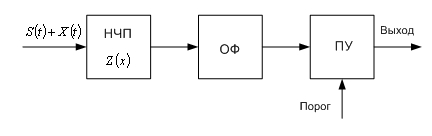
Рис.1. Оптимальный приемник полезного сигнала на фоне негауссовых помех.
Подставив выражение (1) в (4), получим формулу для алгоритма обнаружения:
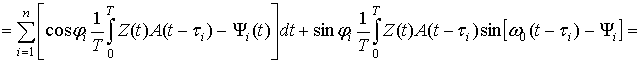 (6)
(6)
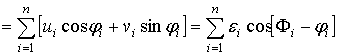 ,
,
где ![]() - квадратурные составляющие обнаруживаемого
сигнала. Из (6) следует, что отношение правдоподобия равно:
- квадратурные составляющие обнаруживаемого
сигнала. Из (6) следует, что отношение правдоподобия равно:
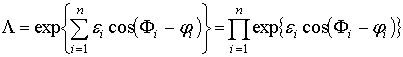 . (8)
. (8)
Усредняя отношение правдоподобия ![]() по случайным фазам
по случайным фазам ![]() , которые распределены
равномерно на интервале:
, которые распределены
равномерно на интервале:
 ,
,
получаем значение усредненной величины:
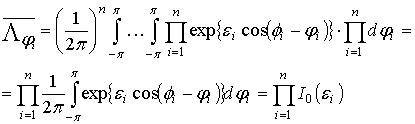 , (9)
, (9)
где ![]() - модифицированная функция
Бесселя нулевого порядка [3]. Из (9) получаем:
- модифицированная функция
Бесселя нулевого порядка [3]. Из (9) получаем:
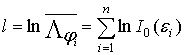 . (10)
. (10)
Полученный алгоритм показывает, что приемник
обнаружения, рис.2, содержит один НЧП и n квадратурных
каналов, в каждом из которых образуются величины ![]() и
и ![]() (7), которые возводятся
в квадрат и поступают на НЧП1 с амплитудной характеристикой
(7), которые возводятся
в квадрат и поступают на НЧП1 с амплитудной характеристикой ![]() .
.

Рис.2. Оптимальный приемник полезного сигнала на фоне негауссовых помех с квадратурными преобразователями.
С выходов всех НЧП1 напряжения поступают на сумматор и далее на пороговое устройство. Структурная схема приемника полезного сигнала с использованием интегральных микросхем производства фирмы Analog Devices [4] изображена на рис.3.
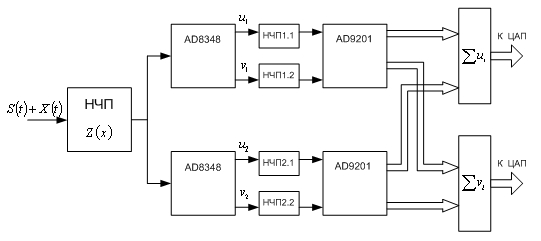
Рис.3. Оптимальный приемник полезного сигнала на фоне негауссовых помех с применением микросхем фирмы Analog Devices.
Используя далее тот факт, что огибающая ![]() может быть получена пропусканием напряжения с
выхода НЧП (с амплитудной характеристикой (5)) через линейный
фильтр, оптимальный для сигнала с любой начальной фазой и
детектированием (линейным), то структура приемника обнаружения упрощается
и состоит из НЧП,
может быть получена пропусканием напряжения с
выхода НЧП (с амплитудной характеристикой (5)) через линейный
фильтр, оптимальный для сигнала с любой начальной фазой и
детектированием (линейным), то структура приемника обнаружения упрощается
и состоит из НЧП, ![]() -
оптимальных фильтров (ОФ),
-
оптимальных фильтров (ОФ), ![]() - квадратичных детекторов (КвД), сумматора
и порогового устройства. По такой блок – схеме можно реализовать приемник
обнаружения сложного сигнала, состоящий из N элементарных
сигналов, рис.4.
- квадратичных детекторов (КвД), сумматора
и порогового устройства. По такой блок – схеме можно реализовать приемник
обнаружения сложного сигнала, состоящий из N элементарных
сигналов, рис.4.
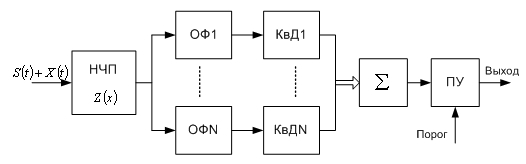
Рис.4. Оптимальный приемник сложного сигнала.
Допустим теперь, что сигнал (1) имеет вид когда
![]() . Тогда из
(6) сразу следует, что:
. Тогда из
(6) сразу следует, что:

![]()
 , (11)
, (11)
где
причем, ![]() и
и ![]() определяются из (7).
Из (11) следует, что
определяются из (7).
Из (11) следует, что
![]() (13)
(13)
На рис.5 изображена блок-схема приемника
обнаружения сигнала (1), реализующая алгоритм (13). Поэтому в силу
монотонности функции ![]() , оптимальный приемник (в принципе
любого по мощности сигнала) состоит из НЧП вида (5),
, оптимальный приемник (в принципе
любого по мощности сигнала) состоит из НЧП вида (5), ![]() - оптимальных
фильтров, сумматора, детектора огибающей (ДО) и порогового устройства, в
котором реализуется алгоритм:
- оптимальных
фильтров, сумматора, детектора огибающей (ДО) и порогового устройства, в
котором реализуется алгоритм:

Рис.5.
Оптимальный приемник с алгоритмом обнаружения вида ![]() .
.
Анализ показывает, что если сигнал (1) является единым сложным сигналом, то появляется возможность единого (когерентного) суммирования по высокой частоте, если устранить частотную расстройку элементарных сигналов и временное запаздывание.
Перейдем теперь к вычислениям характеристик.
Допустим, что распределение величин ![]() и
и ![]() является
нормальным. Неизвестная начальная фаза
является
нормальным. Неизвестная начальная фаза ![]() , имеет релеевское распределение на
интервале
, имеет релеевское распределение на
интервале ![]() :
:
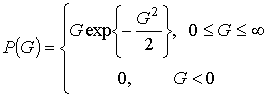 .
.
Если рассмотреть алгоритм (14), то для
отыскания распределения величины ![]() необходимо найти распределение суммы
квадратов случайных величин
необходимо найти распределение суммы
квадратов случайных величин ![]() . В работе [3] были получены как
формулы для распределений случайной величины
. В работе [3] были получены как
формулы для распределений случайной величины ![]() при наличии и при отсутствии
сигнала, так и формулы вероятностей
при наличии и при отсутствии
сигнала, так и формулы вероятностей ![]() и
и ![]() , причем рассмотрены пути упрощения
вычислительной процедуры по полученным достаточно сложным формулам
качества обнаружения. Поэтому воспользуемся сразу полученными формулами.
, причем рассмотрены пути упрощения
вычислительной процедуры по полученным достаточно сложным формулам
качества обнаружения. Поэтому воспользуемся сразу полученными формулами.
Так, например, при отсутствии сигнала в силу стационарности
помехи ![]() , поэтому,
как следует из (7),
, поэтому,
как следует из (7), ![]() , отсюда
, отсюда
а закон распределения приведенный в [3]:
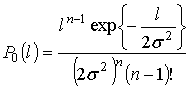 , (16)
, (16)
где дисперсия равна:
причем положено, что ![]() ,
, ![]() , откуда
, откуда ![]() . Из (17) получаем, что:
. Из (17) получаем, что:
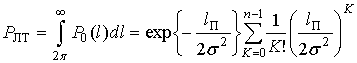 . (18)
. (18)
При малых вероятностях ложной тревоги, когда ![]() , из (18)
получаем:
, из (18)
получаем:
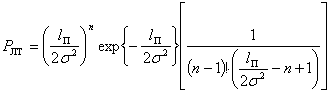 . (19)
. (19)
Пусть теперь сигнал присутствует в (15). Тогда из (7) получаем:
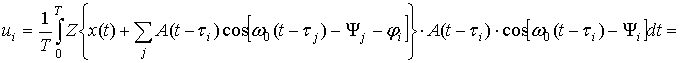
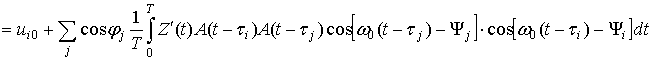 + (20)
+ (20)
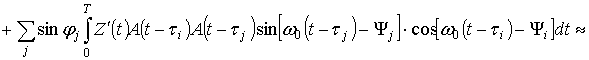
 +
+
+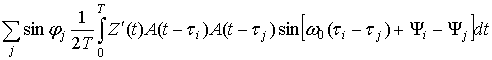 ,
,
где интегралами,
содержащими быстроосциллирующие функции типа ![]() , мы пренебрегаем в силу их малости.
Из (20) с учетом стационарности помехи и выражения для функционала
вероятности
, мы пренебрегаем в силу их малости.
Из (20) с учетом стационарности помехи и выражения для функционала
вероятности ![]() негауссовой
помехи как показано в [2], равного:
негауссовой
помехи как показано в [2], равного:
F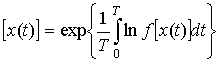 ,
,
где ![]() - одномерная плотность вероятности
негауссовой помехи
- одномерная плотность вероятности
негауссовой помехи ![]() ,
а
,
а ![]() -
интервал наблюдения, равный длительности сигнала, и (15) получаем:
-
интервал наблюдения, равный длительности сигнала, и (15) получаем:
Аналогично для ![]() получаем:
получаем:
Следовательно:
![]() ,
(23)
,
(23)
откуда
Дисперсия же случайной величины ![]() в (7), с учетом
малости сигнала равна (17).
в (7), с учетом
малости сигнала равна (17).
В [3] показано, что распределение величины (14) в этом случае равно:
 ,
, ![]() (25)
(25)
где ![]() - модифицированная функция Бесселя
- модифицированная функция Бесселя ![]() - го порядка,
- го порядка, ![]() определяется (24),
а
определяется (24),
а ![]() – (17).
Вероятность правильного обнаружения равна:
– (17).
Вероятность правильного обнаружения равна:
![]()
 ,
(26)
,
(26)
где функция ![]() есть обобщенная функция
[3]:
есть обобщенная функция
[3]:
 , (27)
, (27)
![]() ,
,  .
.
Если же все ![]() одинаковы, то из (24) следует, что
в отсутствие сигнала
одинаковы, то из (24) следует, что
в отсутствие сигнала 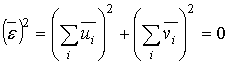 , ибо
, ибо ![]() , а дисперсия, как нетрудно проверить
равна (17):
, а дисперсия, как нетрудно проверить
равна (17):
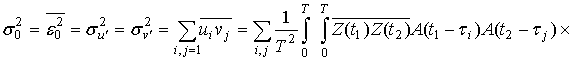
 ,
,
откуда
где были отброшены
интегралы от быстроосциллирующих функций. Вероятность ложной тревоги
при релеевском распределении случайной величины (15) и равенстве
величины ![]() (28)
равна:
(28)
равна:
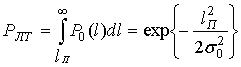 . (29)
. (29)
При наличии сигнала, с использованием (12), (21) и (22), получаем:
![]() , (30)
, (30)
где - 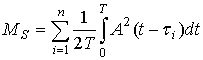 , (31)
, (31)
а дисперсия, в силу
малости сигнала, равна ![]() и определяется (28). Распределение
случайной величины
и определяется (28). Распределение
случайной величины ![]() (15)
в этом случае Райсовское [2], в котором
(15)
в этом случае Райсовское [2], в котором ![]() надо заменить на
надо заменить на ![]() (30), а дисперсию на
(30), а дисперсию на ![]() (28). Вероятность
правильного обнаружения равна:
(28). Вероятность
правильного обнаружения равна:
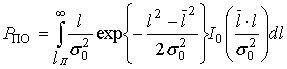 . (32)
. (32)
Отметим, что если сложный сигнал состоит из
элементарных сигналов, то при использовании приемника, выполненного по
блок – схеме рис.6, мощность сигнала (31) равна ![]() , т.е. увеличивается в
, т.е. увеличивается в ![]() раз по сравнению с
мощностью одного элементарного сигнала, что приводит к улучшению
качества обнаружения:
раз по сравнению с
мощностью одного элементарного сигнала, что приводит к улучшению
качества обнаружения: ![]() падает,
падает, ![]() растет.
растет.
Сделаем замечание относительно случая обнаружения сигнала
(1) в нестационарной негауссовской помехе. В этом случае все выражения
для средних и дисперсий, например, (17) и (24) усложняются, ибо как ![]() , так и
, так и ![]() будут явно зависеть
от времени, и вычислять соответствующие интегралы весьма трудно.
будут явно зависеть
от времени, и вычислять соответствующие интегралы весьма трудно.
Литература
1. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации: Учеб. пособие для вузов. – М.: Радио и связь, 1992. – 304 с.: ил.
2. Голяницкий И.А. Оптимальная пространственно – временная обработка негауссовых полей и процессов. - М.: Издательство МАИ, 1994. - 208 с.: ил.
3. Голяницкий И.А. Анализ и оптимизация нелинейных информационных систем. - М.: Издательство МАИ, 1996 г. 178 с.: ил.
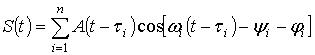 , (1)
, (1)
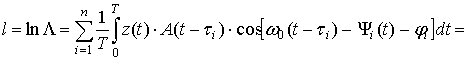
 (7)
(7) 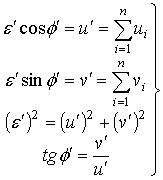 , (1
, (1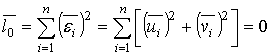 ,
(15)
,
(15) 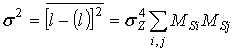 , (17)
, (17)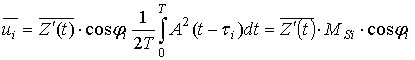 (2
(2 (2
(2 , (28)
, (28)