УДК 537.874.6; 621.396.9
ДИФРАКЦИЯ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ПРЯМОУГОЛЬНОМ ДИЭЛЕКТРИЧЕСКОМ КЛИНЕ. АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ
А. А. Комаров, В. А.
Пермяков
Национальный исследовательский университет Московский энергетический институт,
кафедра Антенных устройств и распространения радиоволн
Получена 3 сентября 2011 г.
Аннотация. Дифракция плоской электромагнитной волны на прямоугольном диэлектрическом клине исследована численно методом интегральных уравнений. Изучены амплитудные и фазовые характеристики полных токов, неравномерных частей токов, поверхностных импедансов, дифракционных полей при различных углах падения плоской волны. Проведено сравнение дифракционных полей с приближением физической оптики.
Ключевые слова. Плоская электромагнитная волна, диэлектрический клин, поверхностные интегральные уравнения, поверхностные токи, поверхностный импеданс, дифракционное поле.
Abstract. Diffraction of electromagnetic waves by a dielectric wedge is numerically analysed using the integral equation method. Amplitude and phase characteristics of the equivalent surface currents, the surface impedances and the scattered fields are analysed in detail for various incident angles of plane wave. The comparison of diffracted fields vs physical optics approximation is carried out.
Keywords: electromagnetic plane wave, dielectric wedge, surface integral equations, surface currents, surface impedance, diffraction field.
Введение
Необходимость определения дифракционных полей, созданных диэлектрическим клином (ДК), возникает во многих прикладных проблемах. Укажем на такие приложения, как формирование электромагнитных (ЭМ) полей покрытиями безэховых камер, в которых широко используются клиновидные структуры [1], распространение ЭМ волн в городе, когда фрагменты домов аппроксимируются прямоугольным ДК [2,3], дифракция ЭМ волн на естественных препятствиях клиновидной формы [4]. Во всех этих случаях для расчета ЭМ полей необходимо решение эталонной задачи дифракции ЭМ волн на ДК.
Эталонная задача формулируется следующим образом. Рассматривается дифракция плоской монохроматической электромагнитной волны, падающей под углом к ребру идеально острого однородного диэлектрического клина с потерями. Необходимо найти структуру ЭМ поля, рассеянного клином, на произвольных расстояниях от клина. Большой интерес для различных практических приложений представляет решение аналогичной задачи возбуждения диэлектрического клина локализованным источником ЭМ волн.
Если бы аналитическое решение такой эталонной задачи, пригодное при произвольных значениях параметров клина и структуры падающей ЭМ волны и удобное для получения асимптотических представлений, было найдено, это позволило бы получить асимптотики, пригодные для вычисления ЭМ поля в дальней зоне, аналогичные формулам неравномерной и равномерной геометрических теорий дифракции (ГТД) для идеально проводящего клина [5,6]. Такое универсальное решение до сих пор не найдено.
В [7] методом собственных функций (МСФ) получено численное решение двумерной задачи дифракции плоской волны на прямоугольном ДК в случае Н-поляризации (вектор напряжённости магнитного поля параллелен ребру клина). Известно также асимптотическое представление дифракции плоской волны на ДК, найденное с помощью интегралов Зоммерфельда-Малюжинца в двумерном случае [8], однако оно использует тонкую аналитическую технику, является достаточно громоздким и также требует численного решения.
В этой ситуации для расчета дифракционного поля от ДК применяют эвристические формулы [9,10], либо используют для описания ДК импедансное приближение и теорию Малюжинца для импедансного клина. Теория Малюжинца и асимптотические формулы для двумерной задачи дифракции плоской волны на импедансном клине приведены в [11,12]. При использовании эвристических формул или аппроксимации ДК импедансным возникает резонный вопрос о применимости подобных приближений.
Альтернативой поиску аналитических решений задачи дифракции на ДК может служить решение, найденное прямыми численными методами. Известны численные решения задачи дифракции ЭМ волн на ДК, полученные методом поверхностных интегральных уравнений (ПИУ) [13-16] и методом конечных разностей во временной области [17]. Спецификой численных методов является необходимость скругления ребра клина, однако при малом радиусе скругления принципиальной разницы между дифракционными полями для идеально острого и скругленного ДК на расстояниях от ребра, больших по сравнению с радиусом скругления, быть не должно, а именно этот случай представляет наибольший практический интерес. Численное решение представляет самостоятельную ценность, поскольку позволяет исследовать структуру ЭМ полей и поверхностного импеданса ДК. Кроме того, оно может быть применено для проверки применимости эвристических решений и импедансного приближения к ДК. Численное решение задачи дифракции на ДК может быть использовано для построения гибридной ГТД в соответствии с идеями, изложенными в [18,19].
Целью данной работы является исследование дифракции плоской ЭМ волны на ДК численным методом. Решение задачи дифракции на ДК со скругленным ребром методом ПИУ было получено Васильевым и Солодуховым в [13-15] для общего случая наклонного падения плоской ЭМ волны под произвольным углом к ребру ДК. Исследование дифракционных полей для ДК на основе этого подхода было проведено в работах [13,14,20,21]. При этом радиус скругления ребра задавался малым по сравнению с длиной волны для того, чтобы рассеянное поле совпадало с полем для идеально острого клина всюду, кроме небольшой области вблизи ребра. Поскольку задача дифракции плоской волны на ДК содержит 5 свободных параметров (2 угла падения плоской волны на ребро ДК, угол раскрыва клина, действительная и мнимая части диэлектрической проницаемости клина), то численное исследование явлений дифракции на всем множестве параметров не укладывается в рамки одной статьи. Исследование данной работы ограничено случаем нормального падения плоской ЭМ волны на ребро прямоугольного клина.
В работе сделан упор на изучение амплитудно-фазовых характеристик дифракционного поля, поверхностных токов и импедансов. Следует отметить, что фазовые характеристики полей, токов и импедансов ранее не были исследованы, за исключением работы [7], в которой была рассчитана фаза поверхностного импеданса прямоугольного ДК в случае Н-поляризации, и докладов [20,21]. В [20,21] было проведено также сравнение численных результатов, полученных методом ПИУ, с эвристическими формулами ГТД для ДК. В данной работе дан развернутый анализ численных результатов по дифракции плоской волны на прямоугольном ДК, кратко изложенных в [20,21]. Результаты работы могут быть полезны для оценки рассеяния ЭМ волн фрагментами зданий и другими искусственными конструкциями, аппроксимируемыми прямоугольным ДК.
1. Методика численного решения и исходные данные для расчётов
В этом пункте кратко обсуждается методика расчёта дифракции плоской гармонической волны на прямоугольном диэлектрическом клине (рис.1) для случая нормального падения волны на ребро клина. Временной множитель exp(iωt). Все линейные размеры ниже даны в безразмерных переменных, полученных делением линейных размеров на длину волны в свободном пространстве. Электрические поля нормированы делением на импеданс свободного пространства, так что размерности электрического и магнитного полей и поверхностных токов после нормировки совпадают, а поверхностные импедансы - нормированы делением на импеданс свободного пространства.
Согласно методу ПИУ для полубесконечных структур [13-15] в задаче дифракции на клине бесконечный контур интегрирования разбивается на три: два полубесконечных контура, идущих на бесконечность от точек, расположенных на противоположных гранях клина на расстоянии в несколько длин волн от вершины клина, и контур конечной длины, охватывающий скруглённую вершину клина (рис.1). При численном решении ИУ для поверхностных токов используется введённое Уфимцевым понятие о равномерных и неравномерных частях токов [22]. При этом положения точек, выделяющих полубесконечные контуры, выбираются таким образом, чтобы на этих контурах можно было пренебречь неравномерными токами.
Равномерные токи на гранях клина определяются в приближении геометрической оптики через параметры падающей плоской волны и коэффициенты Френеля. В результате исходное ИУ по бесконечному контуру клина сводится к ИУ для полных токов на конечном контуре (рис.1). Результатом решения ИУ являются полные токи на конечном контуре, из которых выделяются неравномерные части токов. Через отношения токов вычисляются поверхностные импедансы клина. Дифракционные поля вычисляются с использованием теоремы эквивалентности как асимптотические представления цилиндрической волны в дальней зоне [13-15].
Отметим, что идея выделения геометрооптической части поля на поверхности диэлектрического клина и сведения исходного ИУ к ИУ для дифракционной добавки к полю была предложена также в [23], однако не была практически реализована. Предложенный и реализованный в [13-15] метод решения дифракции волн на бесконечном клине отличается от идеи [23] тем, что ИУ [13-15] строится для полного тока на конечном контуре и в трехмерном случае. Изложение метода ИУ в применении к задаче дифракции на диэлектрическом клине в монографии [24], §2.3, базируется на работе [14].
При проведении конкретных расчетов длина контура АБ (рис.1), на котором решалось ИУ, была задана равной ν=20λ.
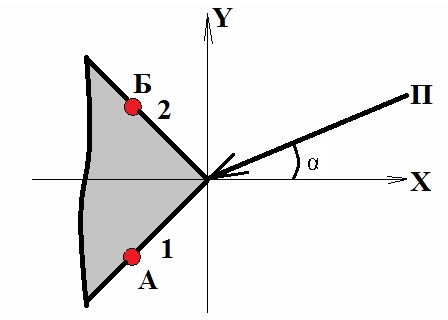
Рис.1. Поперечное сечение клина.
Вдоль контура АБ отсчитывается переменная v; в точке А v = – 10λ, в точке Б v = 10λ, а на ребре клина v =0.
Отметим, что на границах свет-тень падающей и отраженной волн асимптотики амплитуд дифракционных полей [13-15] обращаются в бесконечность. Причина обращения в бесконечность асимптотики амплитуды дифракционного поля в том, что она описывается цилиндрической волной, но на границе свет-тень падающей (отраженной) плоской волны амплитуда дифракционного поля количественно составляет конечную долю амплитуды падаюшей (отраженной) плоской волны, т.е. по отношению к амплитуде цилиндрической волны бесконечно велика.
Расчёты проводились для Е-поляризации (вектор электрического поля параллелен ребру клина) и Н-поляризации (вектор магнитного поля параллелен ребру клина) падающего поля. Ребро клина при численном решении сглаживалось окружностью малого радиуса (r=0,0159λ). Диэлектрическая проницаемость была принята равной ε = 4 – i0,12 , что в диапазоне длин волн 0,3 ÷ 3 м хорошо описывает свойства бетона.
Рассчитывались следующие величины :
1) распределение амплитуд и фаз поверхностных токов по контуру поперечного сечения клина;
2) распределение амплитуд и фаз неравномерных частей поверхностных токов по контуру поперечного сечения клина;
3) распределение модуля и фазы поверхностного импеданса по контуру поперечного сечения клина;
4) зависимости амплитуды и фазы дифракционного поля в дальней зоне от угла наблюдения в плоскости, перпендикулярной ребру клина.
Диапазон углов облучения клина плоской волной α, отсчитываемый от плоскости симметрии клина, менялся в пределах 0о ≤α ≤45о, при этом плоские волны, проникшие внутрь клина, в нем не переотражаются.
2. Облучение прямоугольного диэлектрического клина плоской электромагнитной волной
2.1 Результаты расчётов
Ниже на рис.2 приведены зависимости амплитуд и фаз поверхностных токов от координаты вдоль боковой поверхности клина, на рис.3 – зависимости амплитуд и фаз неравномерных частей поверхностных токов. На всех рисунках, относящихся к токам, использованы следующие обозначения: для Е-поляризации чёрным цветом показан ток Jez, синим – ток Jmv; для Н- поляризации: зелёным цветом – ток Jev, красным – Jmz.
На рис. 4 показаны зависимости модуля и фазы поверхностного импеданса от координаты вдоль боковой поверхности клина, на рис. 5 – зависимости амплитуды и фазы рассеянного поля в дальней зоне от угла наблюдения. Чёрным цветом на этих рисунках показаны зависимости, относящиеся к Е-поляризации, красным – к Н-поляризации волны. Сплошными линиями на рис. 5 обозначены величины, полученные строго по методу ПИУ, штриховыми – в приближении физической оптики (ФО), в последнем случае для расчета полей использовались равномерные части токов, заданные на всем контуре клина.
|
Рис.2. Амплитуды и фазы поверхностных токов;
а) угол облучения α = 0о; б) угол облучения α = 20о; в) угол облучения α = 45о
|
Рис.3. Амплитуды и фазы неравномерных частей токов;
а) угол облучения α = 0о; б) угол облучения α = 20о; в) угол облучения α = 45о
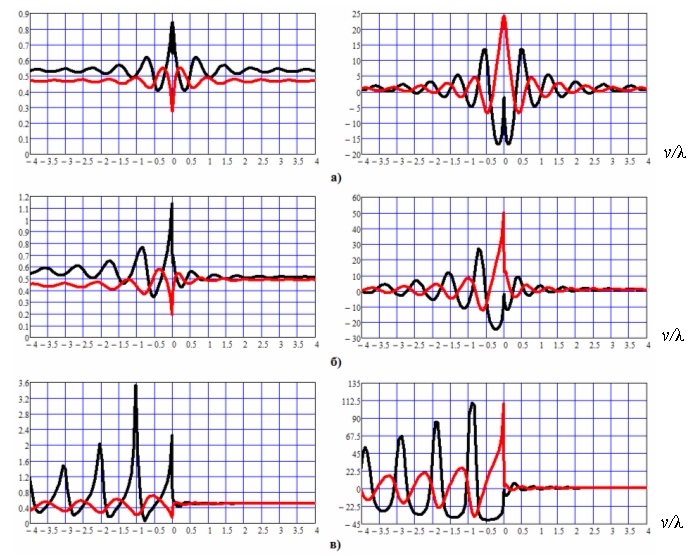
Рис.4. Модули и фазы поверхностных импедансов;
а) угол облучения α = 0о; б) угол облучения α = 20о; в) угол облучения α = 45о
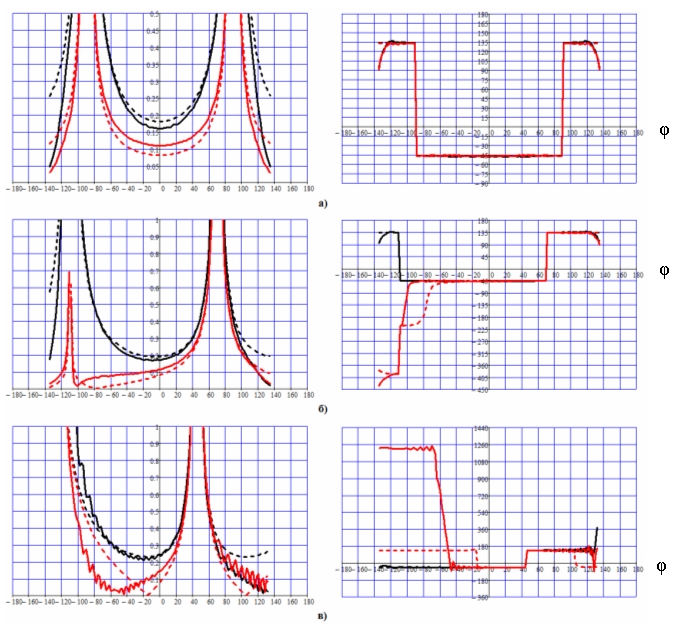
Рис.5. Амплитуды и фазы рассеянных клином полей, как функции угла наблюдения;
а) угол облучения α = 0о; б) угол облучения α = 20о; в) угол облучения α = 45о
2.2. Обсуждение численных результатов.
Поверхностные токи. Из рис. 2 следует, что полные электрические и магнитные токи для обеих поляризаций падающей волны представляют собой сумму осциллирующих неравномерных и постоянных равномерных составляющих. Фазы полных токов Jez, Jmv, Jmz графически совпадают на большей части грани; небольшие различия видны только вблизи вершины клина. Полный ток Jev для Н-поляризации отличается по фазе от остальных токов на 180о.
Законы изменения фаз полных
токов (рис.2, правый столбец) – близки к линейным и согласуются с законом
изменения фаз падающей и отражённой плоских волн, движущихся в свободном
пространстве вдоль плоской границы раздела сред. В приближении геометрической
оптики (ГО) фаза плоской волны вдоль грани клина меняется по закону 
рад, где 
, θ – угол между
нормалью к грани клина и волновым вектором падающей (отраженной) волны,
верхний знак берется на правой, нижний – на левой грани клина, Ф0 –
значение фазы при ν=0.
Модули неравномерных частей токов, осциллируя, стремятся к нулю при движении вдоль направляющей от вершины клина (рис.3, левый столбец). Амплитуды неравномерных токов падают на порядок относительно максимальных значений на расстояниях свыше трёх длин волн (Jmv, Jmz) при симметричном облучении (α=0).
Поведение фаз
неравномерных токов внутри ДК в направлении от вершины приближенно описывается
законом 
, где
- коэффициент
замедления волны неравномерного тока, 
- фазовая скорость волны неравномерного тока
на соответствующей грани клина. Зависимости фаз неравномерных токов от
координаты ν содержат участки, на которых фазы неравномерных
токов меняются достаточно быстро, и чередующиеся с ними участки, на которых
фазы токов меняются практически линейно. Участки с быстрым изменением фазы
включают в себя прилегающие к вершине клина, а также небольшой длины участки, соотствующие
окрестностям минимумов амплитуд токов. Для определенности рассмотрим
неравномерную часть тока Jmν и оценим величину коэф. замедления тока на участках с
практически линейным замедлением фазы тока, в пределах которых отклонение фазы
от линейного закона не превышает 10%. Из численного эксперимента следует, что
коэффициенты замедления этого тока в случае симметричного облучения лежат в
пределах 1,74 … 1,63, т.е. меньше коэф. замедления плоской волны в диэлектрике,
равного 2. При несимметричном облучении (α=20о) коэффицииенты
замедления тока на стороне клина, освещенной под меньшим углом, колеблются в пределах
1,77-1,68, на стороне клина, освещенной под большим углом – в пределах
1,68-1,59.
Колебания амплитуд полных и неравномерных электрических и магнитных токов для обеих поляризаций падающей волны сильнее выражены на грани 1 (v<0) клина, освещенной под большим углом θ относительно нормали к грани (при α=20о θ = 65о), нежели на грани 2 (v>0), освещенной под меньшим углом (при α=20о θ = 25о).
Поверхностные импедансы. Поверхностные импедансы ДК находятся через отношения поверхностных токов
.
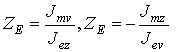(1)
Из рис.4 (левый столбец) следует, что модули импедансов, аналогично модулям токов, имеют неравномерную и равномерную составляющие. Равномерные составляющие импедансов определяются из задачи падения плоской волны перпендикулярной (для клина – Е) поляризации, либо параллельной (для клина – Н) поляризации на диэлектрическое полупространство, как
,
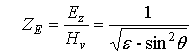. (2)
Так, при α=0, пренебрегая потерями
в среде, получим для равномерной части импеданса Е-поляризации 
, для Н-поляризации 
. Полученные значения
импедансов, как и следовало ожидать, согласуются с результатами расчётов
модулей импедансов на расстояниях от вершины клина, на которых становятся
малыми осцилляции импеданса. На этих же расстояниях фазы поверхностных
импедансов близки к нулю. Значения расстояний, на которых можно пренебречь
осцилляциями модуля и фазы импеданса, существенно зависят от угла падения волны
на грань клина. При симметричном облучении (α=0) – это расстояние свыше
4λ, при несимметричном соответствующие расстояния уменьшаются для грани,
освещенной под меньшим углом падения волны на грань и увеличиваются для грани,
освещенной под большим углом (см. рис. 4 б,в).
Дифракционные поля.
При симметричном
облучении амплитуды дифракционных полей минимальны в направлении обратного
рассеяния и в направлениях вдоль граней клина (рис.5а) . На границах свет-тень
отражённых волн (при углах ±90о относительно плоскости симметрии
клина) дифракционные поля неограниченно растут. Причина этого роста была объяснена выше. Амплитуды дифракционных полей вблизи границ свет-тень для Е-поляризации
выше, чем для Н-поляризации. Фазы дифракционных полей равны приблизительно 45о
в секторе углов наблюдения 
и возрастают скачком на 180о
при выходе за границы этого сектора (рис.5а).
При угле облучения α = 20о вблизи границ свет-тень отражённых волн дифракционные поля растут, причём при угле наблюдения +70о (соответствует грани 2 клина) амплитуды дифракционных полей практически не различаются по величине, а при угле наблюдения – 110о (соответствует грани 1 клина) амплитуда дифракционного поля Е-поляризации существенно превышает амплитуду дифракционного поля Н-поляризации (рис.5б).
Фазы дифракционных полей практически совпадают для двух поляризаций при углах наблюдения более – 90о и качественно различаются вблизи границы свет-тень при меньших углах наблюдения (рис.5б).
При угле облучения α = 45о поведение дифракционного поля для обеих поляризаций в общих чертах, такое же, как и в случае α = 20о. Характерное отличие состоит в том, что при углах наблюдения свыше 45о и меньше 0о амплитуды и фазы дифракционных полей для обеих поляризаций приобретают колебательный характер. Однако по сравнению с поверхностным импедансом уровень колебаний рассеянного поля не очень велик. Причина в том, что дифракционное поле является интегральной характеристикой токов и вклад в поле осциллирующих частей токов при этом сглаживается.
Сравнение результатов расчётов дифракционного поля методом ИУ и и методом ФО показывает, что приближение ФО качественно правильно отражает основные особенности в поведении модуля рассеянного поля почти всюду в диапазоне исследованных параметров клина. Заметные качественные отличия наблюдаются в двух случаях: при углах падения волны, при которых возникают осцилляции дифракционного поля в расчетах по методу ИУ, отсутствующие в приближении ФО, и при углах наблюдения, которым соответствует нуль дифракционного поля в приближении ФО. Наибольшие различия между приближением ФО и расчетом по методу ПИУ наблюдаются для Н-поляризации. При несимметричном облучении клина в случае Н-поляризации минимум поля в расчете по методу ИУ и в приближении ФО достигается при разных углах наблюдения, в случае Е-поляризации – при одном и том же угле наблюдения. Следует отметить принципиальные качественные отличия поведения фазы дифракционного поля в приближении ФО от расчета по методу ПИУ в определенных секторах углов наблюдения при несимметричном облучении ДК.
Заключение
Проведено численное исследование основных характеристик дифракции плоской электромагнитной волны на ДК: поверхностных токов и импедансов, дифракционных полей в дальней зоне ДК. Исследование выполнено для прямоугольного ДК при значении его комплексной диэлектрической проницаемости ε = 4 – i0,12 в двумерном случае (направление падающей волны перпендикулярно ребру клина) для нескольких углов падения плоской волны относительно плоскости симметрии клина. Аналогичные расчеты для клина с проницаемостью ε=3–i0,06 показали, что вариации диэлектрической проницаемости в пределах принятых исходных данных не приводят к принципиальным изменениям, отражаясь прежде всего на фазовых характеристиках неравномерных частей токов.
Принципиальным моментом, отличающим данную работу от других работ по ДК, является исследование фазовых характеристик токов, импедансов и дифракционного поля.
Поверхностные импедансы граней ДК являются осциллирующими функциями координаты в тех же пределах, что и неравномерные части токов. Существование заметных осцилляций поверхностного импеданса ДК указывает на принципиальное отличие процесса дифракции на ДК от импедансного клина. Однако вопрос об аппроксимации ДК импедансным для расчета дифракционных полей заслуживает отдельного исследования, т.к. дифракционные поля являются интегральными характеристиками токов и вклад осциллирующих частей токов в поле при этом может сглаживаться.
Наибольшие различия между приближением ФО и расчетом по методу ПИУ наблюдаются для Н поляризации при несимметричном облучении клина.
В заключение подчеркнем, что данная работа существенно опирается на результаты пионерских исследований проф. Васильева Е.Н. и доц. Солодухова В.В. [13-15].
Литература
1. Балабуха Н.П., Зубов А.С., Солосин В.С. Компактные полигоны для измерения характеристик рассеяния объектов. –М.: Наука, 2007. -266 с.
2. R.P. Torres a.o. CINDOOR: An Engineering Tool for Planning and Design of Wireless System in Enclosed Spaces. // Antennas and Propagation Magazine, 1999, vol. 41, No.4. pp. 11-21.
3. Пермяков В.А., Жексенов М.А. Методы расчета распространения радиоволн в городе (обзор). /Излучение и рассеяние электромагнитных волн. ИРЭМВ-2009. Труды международной научной конференции. Таганрог – Дивноморское, Россия, июнь 27- июль 1, 2009, с. 48-52
4. Черенкова Е.Л., Чернышов О.В. Распространение радиоволн. –М.:, Радио и связь, 1984. 272 с.
5. Боровиков В.А., Кинбер Б.Е. Геометрическая теория дифракции. –М.: Связь, 1978. – 248 с.
6. Kouyoumjian R.G., Pathak P.H. A Uniform Geometrical Theory of Diffraction for an Edge in an Perfectly Conducting Surface. // Proc. IEEE. 1974, vol. 62, No.11, pp. 1448- 1461
7. Jones D.S. Impedance of a lossy wedge. IMA Journal of Applied Mathematics (2001), 66, 411-422.
8. Крячко А.Ф., Лихачев В.М., Смирнов С.Н., Сташкевич А.И. Теория рассеяния электромагнитных волн в угловых струтурах. СПб.: Наука, 2009, -194 с.
9. Luebbers R.J. Finite Conductivity Uniform GTD Versus Knife Edge Diffraction in Prediction of Propagation Path Loss. // IEEE Trans. Antennas Propagat. , vol. 32, No. 1, 1984, pp. 70-76
10. Holm P.D. A New Heuristic UTD Diffraction Coefficient for Nonperfectly Conducting Wedges. // IEEE Trans. on Antennas and Propagation, vol. 32, No. 2, 1984, pp. 175-177.
11. Osipov A.V., Norris A.N. The Malyuzhinets theory for scattering from wedge boundaries: a review. Wave motion, 29, (1999), pp. 313-340.
12. Norris A.N., Osipov A.V. Far-field analysis of the Malyuzhinets solution for plane and surfase waves diffraction by an imedance wedge. Wave motion, 30, (2000), pp. 69-89.
13. Васильев Е.Н., Солодухов В.В. О дифракционных коэффициентах для диэлектрического клина. //В сб. Теория дифракции и распространения волн. т.1. VI Всесоюзный симпозиум по дифракции и распространению волн. 1973. С. 238-242.
14. Васильев Е.Н., Солодухов В.В. Дифракция электромагнитных волн на диэлектрическом клине. //Известия ВУЗов, Радиофизика, 1974, т. 17, № 10, с. 1518-1528.
15. Васильев Е.Н., Солодухов В.В. Метод интегральных уравнений в зададчах дифракции на полубесконечных диэлектрических структурах. Препринт № 25(397), -М.: ИРЭ РАН СССР, 45 с.
16. Vasil’ev E.N., Soloukhov V.V., Fedorenko A.I. The integral equation method in the problem of electromagnetic waves difraction by complex bodies. // Electromagnetics, V.11, No.2, 1991, pp. 161-182.
17. Rouviere J.F., Douchin N., Combes P.F. Diffraction by a Lossy Dielectric Wedges Using Both Heuristic UTD Formulation and FDTD. // IEEE Trans. on Antennas and Propagation, vol. 47, No. 11, 1999, pp. 1702- 1708.
18. Васильев Е.Н., Солодухов В.В. Гибридные геометрическая и физическая теории дифракции. // Труды 11-й всероссийской школы – конференции по дифракции и распространению волн. М.: МГУ. 1998. С. 5-17.
19. Vasil'ev E.N., Solodukhov V.V. Hybrid Geometrical Theory of Diffraction. // Journal of Communication Technology and Electronics, vol. 45, Suppl. 2, 2000, pp. 184-195.
20. Пермяков В.А., Жексенов М.А., Комаров А.А. Сравнение дифракционных полей от диэлектрического клина, полученных методом интегральных уравнений и в приближении равномерной геометрической теории дифракции. //ИРЭ РАН , 3-я Всероссийская научно – техническая конференция «Радиолокация и радиосвязь», Москва, 26-30 октября 2009 г., доклады, Москва, 2009 г. , электронное издание, с. 682-686.
21. Пермяков В.А., Жексенов М.А., Комаров А.А. О применении равномерной геометрической теории дифракции к анализу дифракционных полей от диэлектрического клина. //Космическая радиолокация (электронный ресурс). Всероссийские радиофизические чтения –конференции памяти Н.А.Арманда. Сб. докладов научно-практической конференции (Муром, 28 июня-1 июля 2010 г). – Муром, изд. полиграфический центр МИВЛГУ, 2010, - 307 с., - 1 электронно-оптический диск. № гос. регистрации 0321001174, с. 264-269.
22. Уфимцев П.Я. Метод краевых волн в физической теории дифракции. –М.: Сов. Радио, 1962, - 243 с.
23.Нефедов Е.И., Сивов А.Н. К задаче дифракции на бесконечном однородном диэлектрическом клине. Препринт ИРЭ АН СССР №80, М., 1971, 13 с.
Нефедов Е.И., Сивов А.Н. Геометрооптическое решение задачи о диэлектрическом клине. / РиЭ, 1974, т.19, №4, с. 824-827.
24.Нефедов Е.И. Дифракция электромагнитных волн на диэлектрических структурах. М.: Наука, 1979, - 272 с.