УДК 535.361.2

ДЕТЕКТИРОВАНИЕ ПОГЛОЩАЮЩЕЙ НЕОДНОРОДНОСТИ БИОЛОГИЧЕСКИХ ТКАНЕЙ В ДИФФУЗИОННОЙ ОПТИЧЕСКОЙ ТОМОГРАФИИ НА ОСНОВЕ ПОЗДНО ПРИШЕДШИХ ФОТОНОВ

С. Г. Проскурин, С. В. Фролов, А. Ю. Потлов

«Энергетический факультет» ФГБОУ ВПО «Тамбовский государственный технический университет», кафедра «Биомедицинская техника»

Получена 20 августа 2012 г., после доработки – 4 сентября 2012 г.

Аннотация. Описан новый метод непосредственной регистрации оптической неоднородности (гематомы, кисты, опухоли) в биологической ткани, до реконструкции изображения с помощью диффузионной оптической томографии (ДОТ). Метод основан на регистрации поздно пришедших фотонов (ППФ рассеивающихся и диффузно проходящих через биообъект или фантом. В экспериментальной части исследования используются импульсный фемтосекундный лазер близкого ИК диапазона, в качестве излучателя, и стрик камера с линейкой детекторов, в качестве приёмника излучения. В теоретической части рассматривается модель диффузии исходного числа фотонов в импульсе – модель капли, со временем равномерно заполняющей объект и движущейся к его центру.

Ключевые слова: диффузионная оптическая томография (ДОТ), поздно пришедшие фотоны (ППФ), регистрация неоднородности, оптические свойства биообъектов.

Abstract. A new method of immediate inhomogeneity detection (hematoma, cyst, tumour), which is determined prior of image reconstruction by means of diffuse optical tomography (DOT). The method is based on detection of late arriving photons (LAP), which are scattered and diffusely travel through biological object or a phantom are used for the purpose. In experiment, near infrared femtosecond pulsed laser is used as a source of irradiation. Streak camera with detection array is used as a detector. Theoretical part describes diffusion model of a bunch of photons – model of a drop, which uniformly fills the object with time and moves to the center of it.

Keywords: diffuse optical tomography (DOT), inhomogeneity detection, late arriving photons (LAP), optical properties of biological objects.

Введение

Диффузионная оптическая томография (ДОТ) — перспективный томографический метод исследования тканей, основанный на физическом явлении диффузии и на различном поглощении света оксигенированной и неоксигенированной кровью. Метод базируется на измерении интенсивности излучения регистрируемого после многократного рассеяния (диффузии фотонов) внутри биообъекта.

При использовании импульсного источника излучения, в первую очередь, принято обращать внимание на начальную часть (рис.1) кривой временной функции рассеяния точки (ВФРТ). Область I, соответствует рано пришедшим фотонам [1,2], область II (средняя часть) характеризует среднее время пролета фотонов [3-5]. В подавляющем большинстве работ по ДОТ, используют именно первые две части [1-5]. Авторами предлагается использовать и последнюю часть диффузно прошедшего излучения ВФРТ (область III). Эта область соответствует поздно пришедшим фотонам [6,7]. Важно отметить, что поздно пришедшие фотоны практически не вносят вклада в вычисление среднего времени пролета диффузно прошедшего импульса излучения [8,9].

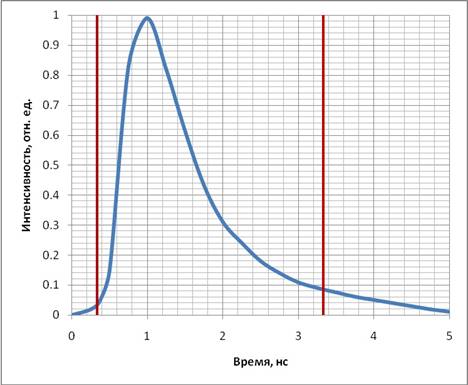
Рис.1. Временная функция рассеяния точки – оптический импульс диффузно прошедший через сильно рассеивающую среду

В данной работе предлагается модель капли – импульса излучения с фиксированным исходным числом фотонов, который падает на объект около поверхности и диффундирует (расплывается) по нему с преимущественным движением к центру объекта. Такая модель рассматривается как, единственная возможность описать экспериментально полученные данные, как для однородного, так и для неоднородного случаев. Эта модель представляет собой решение уравнение переноса излучения в диффузионном приближении [1, 2]:

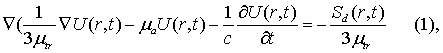
где U (r,t) – диффузионная составляющая лучистой энергии; – транспортный коэффициент экстинкции, который есть сумма коэффициента поглощения и редуцированного коэффициента рассеяния – ; g – параметр анизотропии рассеяния; – функция источника оптического излучения.

С другой стороны, согласно микроскопическому закону Бэра-Ламберта, ВФРТ, как решение уравнения (1), может быть представлена в виде мультипликативной функции: произведения независимо рассеивающей и независимо поглощающей компоненты:

где I_o – исходная интенсивность излучения, которая соответствует числу фотонов в одном импульсе; c_n – скорость света в среде с показателем преломления n; индекс i = 1,2 обозначает две рассеивающие среды с двумя разными показателями поглощения.

Материалы и методы исследований

В экспериментальной установке (рис. 2) качестве источника импульсного излучения в используется фемтосекундный титан-сапфировый лазер с синхронизацией мод MIRA 900-B (Coherent) и выводом излучения через световод на исследуемый объект.

Рис.2. Фотография экспериментальной установки.

Накачка импульсного лазера осуществляется излучением непрерывного аргонового лазера INNOVA 307 (Coherent). В качестве фантома используется цилиндр, изготовленный из эпоксидной смолы с добавлением наночастиц оксида титана TiO₂со средним диаметром 3 мкм [9]. Концентрация частиц была подобрана таким образом, чтобы редуцированный коэффициент рассеяния был таким же, как у биологических тканей. Для моделирования поглощающей неоднородности в материал, из которого был изготовлен цилиндр, добавлялся специальный краситель с известными спектральными свойствами, чтобы увеличить коэффициент поглощения μ_a (рис.3). Диаметр цилиндра составлял 68 мм, высота также равна 68 мм. Регистрирующие излучение световоды собраны в один пучок и доставляют сигнал к линейке детектора Streak Camera C4334 (Hamamatsu Photonics KK) с временным разрешением 10 пс. Измерения интегральной интенсивности непрерывного излучения проводятся с помощью этого же прибора, но с выключенной временной разверткой. Часть излучения попадает на триггер и контролируется измерителем мощности и длины волны.

Большой динамический диапазон детектируемого сигнала, порядка 10¹⁶, создает существенные трудности для получения абсолютных величин R’(a,t) и =ln[R’(a,t)] [10-12]. Поэтому ранее, как правило, измерялся нормированный на максимум сигнал, основное внимание уделялось форме ВФРТ для линейной и логарифмической шкал интенсивности.

Чтобы получить все кривые диффузно прошедшего излучения R(a, t) в одном масштабе и с учетом абсолютной величины интенсивности, был предложен поэтапный метод измерений [8]. На первом этапе детектировался интегрированный сигнал

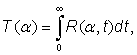
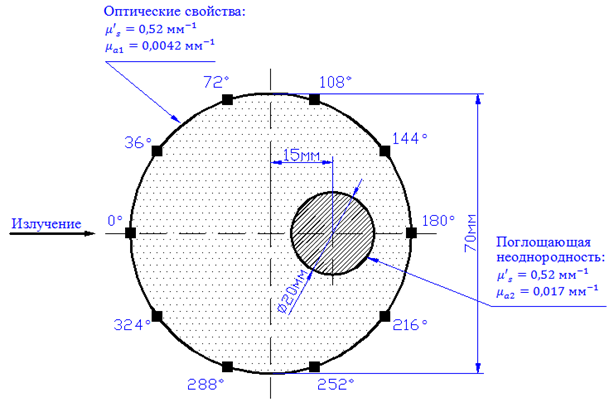
Рис.3. – Поперечное сечение исследуемого фантома с выбранными оптическими свойствами

а на втором этапе детектировалась только форма диффузно прошедшего импульса (ВФРТ – зависимость интенсивности от времени) без учета абсолютной величины интенсивности. Результаты при различных углах вычислялись по следующей формуле:

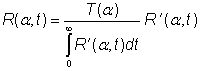
Непосредственная регистрация оптической неоднородности в эксперименте проводилась на основе набора измеренных значений амплитуды и фазы рассеянного излучения. В основе этого алгоритма лежат методы теории возмущений, в соответствии с которыми пространственные разделенияи в зондируемом объекте представляются в следующем виде [13]:

Уравнение Гельмгольца должно быть заменено уравнением для возмущений значений интенсивности диффузионной составляющей:

где λ – параметр; K и D₀ соответствуют невозмущённым параметрам объекта; определяется возмущениями и . Комплексное значение амплитуды волны фотонной плотности представляется как разложение в ряд по степеням λ:

где член порядка N определяется рекуррентным соотношением:

;

r_dопределяет положение приёмника; G(r, r_d) – функция Грина для уравнения Гельмгольца.

Для многих приложений коэффициент можно считать постоянным по всему объёму объекта, а флуктуации - малой и плавно изменяющейся величиной. В данном случае , и только линейный член в разложении ряда может рассматриваться при определении амплитуды и фазы волны фотонной плотности. Разбивая зондируемый объект на n элементов размером h, можно свести задачу восстановления к решению системы линейных уравнений [13]:

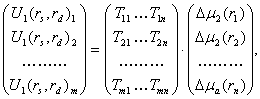
Результаты и обсуждение

Рассмотренную в данной работе диффузионную модель капли нам удалось реализовать в виде специализированного программного продукта, используя численное моделирование на языке C# . На программный продукт получено свидетельство о государственной регистрации программы для ЭВМ в ФПИС [14]. В качестве вычислителя используется CPU (центральный процессор) компьютера, а не GPU (графический процессор), т.к. алгоритм программы не предусматривает распараллеливание. В дальнейшем для увеличения производительности вычислений планируется усовершенствование этого алгоритма под использование графического процессора [15].

Сравним данные полученные в результате моделирования с данными эксперимента для однородного случая. На рис. 4 показаны ВФРТ для двух позиций световодов детектора – 36º и 180º . В этом случае и экспериментальные и расчётные кривые, ln[R(a, t)], сходятся в одну линию. Виртуальный изотропный источник (ВИИ) пакета фотонов движется от поверхности объекта к его центру. После определённого времени, 2,5-3 нс, можно считать, что ВИИ находится в центре объекта. Это означает, что регистрация поздно пришедших фотонов эквивалентна ситуации, когда источник излучения помещен в центр объекта. Такая ситуация аналогична диффузии капли флуоресцирующей краски (отсюда название – модель капли), падающей у поверхности объекта и со временем равномерно заполняющей всё его сечение. В целом, диффузионное приближение работает достаточно эффективно. Особенно хорошее совпадение наблюдается после первой наносекунды. Для угла 36˚ и времени меньше наносекунды диффузионное приближение работает существенно хуже, что говорит о необходимости использовать именно поздно пришедшие фотоны.

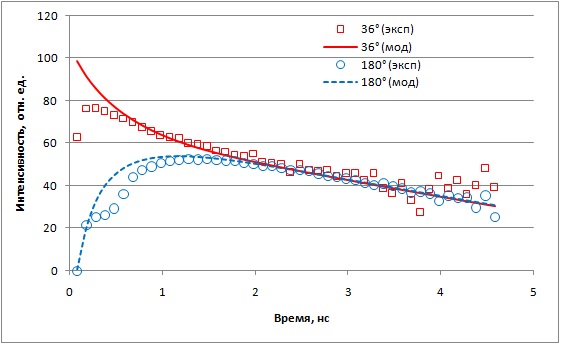
Рис.4. Данные сравнения эксперимента и численной модели для 36º и 180º, соответствующих однородному объекту

Диффузионное приближение движущегося к центру ВИИ дает возможность решать задачу ДОТ в два этапа:

1. непосредственное детектирование неоднородности без решения обратной задачи,

2. восстановление карты распределения неоднородностей – собственно томография.

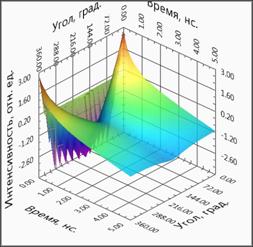
Если все кривые разместить на трехмерном рисунке то, в однородном случае получится плоскость, а в неоднородных – плоскости с провалами на тех углах, рядом с которыми находится неоднородность (рис.5). Такое трехмерное представление данных, для всех несимметричных случаев, позволяет непосредственно, без решения обратной задачи определить наличие или отсутствие неоднородности в режиме реального времени.

(а) (б)

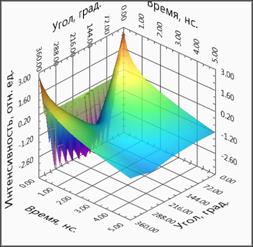
(в) (г)

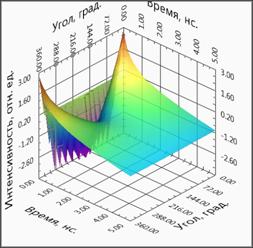
(д)

Рис.5. Трехмерное представление временных зависимостей ВФРТ для различных случаев. Представлены результаты моделирование соответствующий поглощающей неоднородности, расположенной около 0˚ (а), около 90˚(б), около 180˚ (в), около 270˚ (г) и однородному случаю (д). В однородном случае 3D поверхность в области ППФ является плоской, без провалов

Кроме 3-D визуализации ВФРТ, также предлагается использовать индекс неоднородности – HI, который представляет собой зависимость от времени стандартного отклонения от его средних значений для N детектируемых точек и вычисляется по следующей формуле:

где - угол, под которым располагается соответствующий световод. Результаты вычисления индекса неоднородности (HI) для различных случаев представлены на рис. 6.

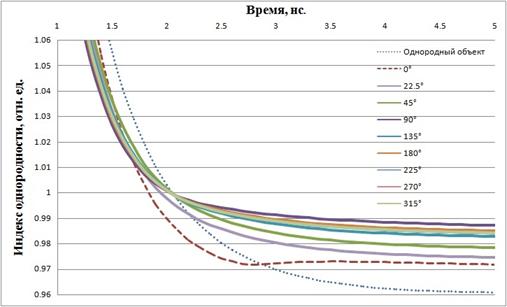
Рис 6. Зависимость индекса неоднородности HI от времени для однородного объека и при наличии неоднородности для 0˚, 22.5˚, 45˚, 90˚, 135˚, 180˚, 225˚, 270˚ и 315˚

В случае однородного объекта HI(t) стремится к нулю, а при наличии неоднородности зависимости стремятся к параллельным оси времени прямым. Минимум HI(t) наблюдается, когда поглощающая неоднородность находиться около угла .

Заключение

Экспериментально и при помощи численного моделирования было показано, что виртуальный изотропный источник оптического излучения движется от поверхности объекта к его центру, а не сквозь него, как это считалось раньше. Т.е. измерение поздно пришедших фотонов эквивалентно ситуации, когда световод источника помещён непосредственно в центр объекта. Диффузионное приближение и модель капли движущейся к центру дают возможность по-новому подойти к решению задачи оптической диффузионной томографии с разделением её на два этапа. Первый этап – это быстрое детектирование неоднородности без решения обратной задачи; второй этап – восстановление карты неоднородностей с решением обратной задачи, собственно томография.

Дальнейшая работа будет сконцентрирована на достижении более точного соответствия результатов эксперимента и численного моделирования. Особый интерес представляют случаи, когда неоднородности разных размеров расположены близко к центру объекта.

Литература

1. Dehghani B.H., Srinivasan S., Pogue B.W., Gibson A. Numerical modeling and image reconstruction in diffuse optical tomography // Mathematical, Physical and Engineering Sciences. – 2009. – V.9. – P.3073–3093.

2. Gibson A., Dehghani H. Diffuse optical imaging // Mathematical, Physical and Engineering Sciences. – 2009. – V.9. – P.3055–3072.

3. Orlova A.G., Turchin I.V., Plehanov V.I., Shakhova N.M., Fiks I.I., Kleshnin M.I., Konuchenko N.Yu., Kamensky V.A.. Frequency–domain diffuse optical tomography with single source–detector pair for breast cancer detection // Laser Physics Letters. – 2008. – №4. – P. 321–327.

4. Клешнин М.С., Турчин И.В.. Спектрально–разрешенная диффузионная флуоресцентная томография биологических тканей // Квантовая электроника. – 2010. – №6. – C. 531–537.

5. Arridge S.R., Hebden J.C., Schweiger M., Schmidt F.E.W., Fry M.E., Hillman E.M.C., Dehghani H., Delpy D.T.A method for 3D time–resolved optical tomography // International Journal of Imaging Systems and Technology. – 2000. – P.2–11.

6. Коновалов А.Б., Власов В.В., Калинцев А.Г., Кравценюк О.В., Любимов В.В. Импульсная диффузионная оптическая томография на основе использования аналитических статистических характеристик траектории фотонов // Квантовая электроника. – 2006. – №11. – C. 1048–1055.

7. Третьяков Е.В., Шувалов В.В., Шутов И.В. Быстрые приближенные статистические нелинейные алгоритмы для решения задач диффузионной оптической томографии объектов со сложной внутренней структурой. // Квантовая электроника, 2001. – Т.31, С. 1095–1100.

8. Proskurin S.G. Late Arriving Photons in Diffuse Optical Tomography // Saratov Fall Meeting – SFM’11/ Saratov, Russia, 2011.

9. Проскурин С.Г. Использование поздно пришедших фотонов для диффузионной оптической томографии биологических объектов. // Квантовая электроника, 2011. – Т. 41. – С. 402–406.

10. Кириллин М.Ю., Меглинский И.В., Приезжев А.В. Влияние кратностей рассеяния на формирование сигнала в оптической низко-когерентной томографии сильно рассеивающих сред // Квантовая электроника, 2006.-№3.- С.247-252.

11. Kravtsenyuk O.V., Lyubimov V.V., Kuzmin V.L., Meglinskiǐ I.V. Diffuse optical tomography of dynamic inhomogeneities in randomly inhomogeneous media // Optics and Spectroscopy, 2006.- Т.100.-№ 6.-С. 950-957.

12. Konovalov A.B., Vlasov V.V., Mogilenskikh D.V., Kravtsenyuk O.V., Lyubimov V.V. Algebraic reconstruction and postprocessing in one-step diffuse optical tomography // Quantum Electronics, 2008.- № 6.-P. 588-596.

13. Зимняков Д.А., Тучин В.В. Оптическая томография тканей // Квантовая электроника. – 2002. – № 10. – С. 849–867.

14. Свидетельство о государственной регистрации программы для ЭВМ в ФПИС №2012615093 «Моделирование рассеяния света в биологической ткани»/ С.Г. Проскурин, С.В. Фролов, А.Ю. Потлов (RU). Зарегистрировано в реестре программ для ЭВМ 07.06.2012 г.

15. Фикс И.И. Использование графических процессоров для решения задачи распространения света в диффузионной флуоресцентной томографии методом Монте-Карло // Вестник Нижегородского университета им. Н.И. Лобачевского, 2011.-№ 4 (1).- С. 190–195.