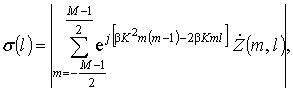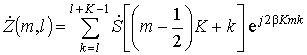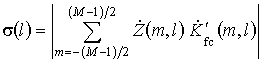Анализ модифицированных алгоритмов формирования радиолокационных изображений.

УДК 621.396

АНАЛИЗ МОДИФИЦИРОВАННЫХ АЛГОРИТМОВ ФОРМИРОВАНИЯ РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ

С. М. Зраенко

Уральский федеральный университет имени первого Президента России Б.Н.Ельцина

Получена 26 августа 2013 г.

Аннотация. Проведено исследование модифицированных алгоритмов кусочно-линейной аппроксимации применительно к обработке сигналов в радиолокаторе с синтезированной апертурой. Определены их вычислительная эффективность и качественные параметры формируемого изображения. Приведены структурные схемы трех модификаций алгоритма и представлены результаты их анализа по требуемой разрядности вычислений.

Ключевые слова: модифицированные алгоритмы кусочно-линейной аппроксимации, вычислительная эффективность, параметры изображения, разрядность вычислений.

Abstract: A study of modified algorithms piecewise linear approximation with respect to signal processing in synthetic aperture radar. Determine their computational efficiency and the quality parameters of the generated image. Shows a block scheme of the three versions of the algorithm and the results of their analysis on the required bit computing.

Key words: modified algorithms of piecewise linear approximation, computational efficiency, image parameters, bit computing.

1. Введение

Формирование радиолокационного изображения (РЛИ) в радиолокаторе с синтезированной апертурой (РСА), установленном на космическом аппарате, характеризуется высокими требованиями к производительности и объему оперативной памяти вычислителя. Кроме этого, в космических РСА возникает необходимость учета линейного и квадратичного смещений элементов по дальности за время синтезирования апертуры, вызванных, прежде всего, вращением Земли и существенной кривизной фазового фронта отраженной волны. Вместе с тем, дополнительным требованием, предъявляемым к таким системам, может являться необходимость реализации предельного разрешения (использование при синтезировании апертуры всего сигнала принимаемого бортовой антенной от каждого элемента цели) для максимизации отношения сигнал/шум в формируемом изображении [1]. Последнее обстоятельство приводит к необходимости использования квазинепрерывного режима смены информации при обработке траекторного сигнала (рис. 1).

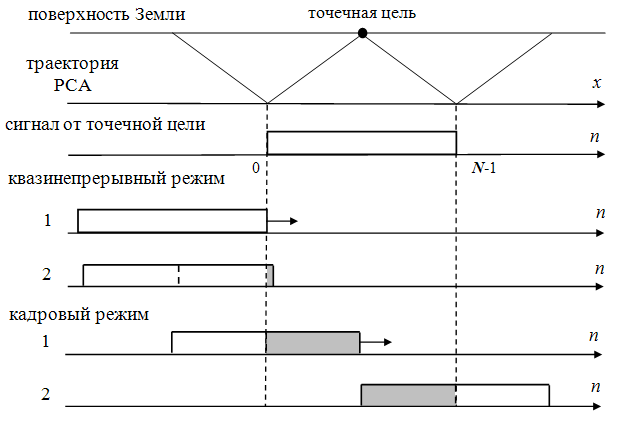
Рис. 1. Сигнал, принятый от точечной цели; кадровый и квазинепрерывный режимы смены данных при синтезировании апертуры.

На рисунке цифрами 1 и 2 обозначены соседние взаимные положения пачки импульсов отраженных от точечной цели и окна обработки. Для кадрового режима смены данных представлена наихудшая ситуация с точки зрения потерь в разрешении и энергетике для формируемых пикселей изображения. Необходимость использования квазинепрерывного режима смены информации при синтезировании апертуры может быть также связана и с ограничениями на объем оперативной памяти, выделяемой для выполнения процедуры формирования РЛИ [1]. Одновременно указанным условиям удовлетворяет алгоритм дискретной свертки, который, однако, требует выполнения большого количества операций, что ограничивает возможности вычислительного устройства по оперативному анализу формируемого изображения. Одним из возможных решений здесь может быть применение при обработке приближенных по точности формирования РЛИ алгоритмов, к которым, в частности относятся так называемые алгоритмы кусочно-линейной аппроксимации.

2. Алгоритмы кусочно-линейной аппроксимации

Данные алгоритмы базируются на методе кусочно-линейной аппроксимации, в котором квадратичная опорная фазовая функция, соответствующая идеальному фокусированию, заменяется касательными к ней отрезками [2]. В этом случае весь интервал синтезирования длительностью N отсчетов сигнала разбивается на M сегментов по K отсчетов в каждом. При этом выражение для l-го пикселя РЛИ в одном канале дальности можно представить в виде:

(1)

где m – номер сегмента, – параметр квадратичного закона изменения фазы вдоль траектории РСА (), – длина волны зондирующего колебания, – наклонная дальность от РСА до элемента цели, – скорость носителя РСА, – период дискретизации принимаемого сигнала, – номер отсчета входного сигнала, а – результат обработки внутри сегмента:

. (2)

Здесь k – номер отсчета внутри сегмента, а – сжатые по дальности отсчеты траекторного сигнала.

Таким образом, в пределах сегментов после цифрового гетеродинирования производится суммирование, а для объединения сегментов требуется выполнить коррекцию фазы, обратное гетеродинирование, задержку и суммирование результатов обработки в каждом (рис. 2).

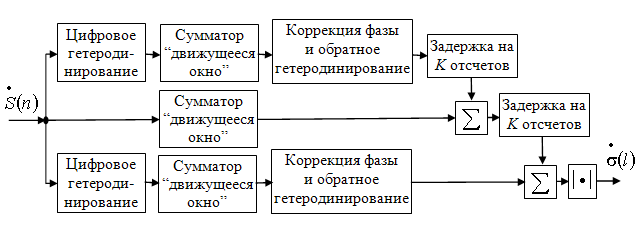
Рис. 2. Структура алгоритма формирования РЛИ методом кусочно-линейной аппроксимации для трех сегментов.

Следствием аппроксимации опорной функции являются уменьшение главного и появление дифракционных максимумов в результирующей диаграмме направленности синтезированной апертуры (ДНСА), уровень которых регулируется выбором длительности сегментов. Размер сегментов можно также согласовать со смещением элементов по дальности за время синтезирования, что позволит упростить его коррекцию. Выигрыш в быстродействии при использовании данного метода обеспечивается за счет распараллеливания на M каналов (процессоров) и за счет упрощения обработки данных в каждом сегменте (нефокусированного синтезирования). Для получения одного пикселя выходного изображения при синтезировании апертуры из N отсчетов здесь требуется выполнить 2(M-1) комплексных умножений, что, как правило, на один- полтора порядка меньше по сравнению с обычной сверткой и (N-1) комплексное сложение. Однако объем оперативной памяти (2N-K) комплексных слов для реализации данного алгоритма приблизительно в два раза больше, чем при реализации алгоритма прямой свертки.

Достоинствами алгоритма являются при квазинепрерывной смене информации пониженные требования к производительности процессора, а также простота коррекции смещения элементов дальности и возможность оценивания доплеровских параметров сигнала и их введения в алгоритм обработки на этапе объединения сегментов. Недостатками – приблизительно в два раза больший требуемый объем оперативного запоминающего устройства (ОЗУ) по сравнению с алгоритмом прямой свертки и несколько больший уровень боковых лепестков.

Для уменьшения требуемого объема памяти предложена модификация базового алгоритма кусочно-линейной аппроксимации (1), (2), полученная из него без введения дополнительных приближений, снижающих качество формируемого РЛИ [1]. При его разработке использовано то обстоятельство, что стоящие под знаком суммы в (2) произведения

где при формировании следующего пикселя РЛИ изменяют свое относительное положение в пределах сегментов, но не изменяются по величине. Коррекция же данных произведений (частичных произведений) происходит только при их переходе в следующий сегмент. Объединение отсчетов в сегментах здесь, в отличие от базового алгоритма, заменено на уточнение сегментных сумм – добавление входящего и вычитание выходящего из сегмента частичного произведения. Таким образом, базовый алгоритм кусочно-линейной аппроксимации преобразован из параллельной в последовательную структуру (рис. 3), в которой вновь входящий отсчет умножается на «коэффициент входа» , переходящий в следующий сегмент отсчет умножается на «коэффициент коррекции» , а перед объединением сегментные суммы умножаются на «коэффициент фазовой коррекции и обратного гетеродинирования» :

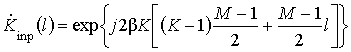. (3)

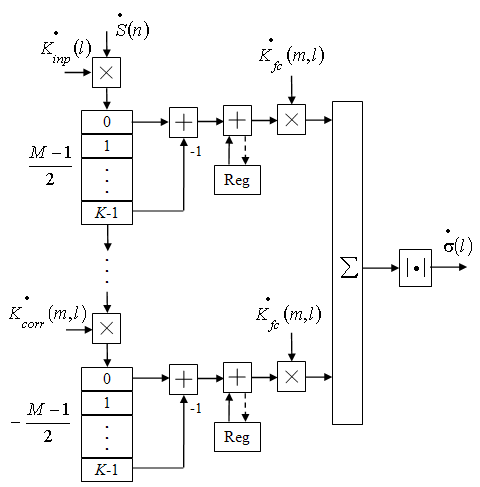
Рис. 3. Структура первого модифицированного алгоритма кусочно-линейной аппроксимации.

Требуемый для реализации алгоритма объем памяти включает M запоминающих устройств, объемом K комплексных слов каждое, для хранения частичных произведений в сегментах и M запоминающих устройств, объемом одно комплексное слово, для хранения сегментных сумм. Для формирования пикселя РЛИ в одном канале дальности для данного алгоритма требуется 2M комплексных умножений и 3M-1 комплексных сложений (2M – на корректирование сегментных сумм, M-1 – на их объединение).

Таким образом, модифицированный вариант алгоритма формируется из базового без введения дополнительных приближений, а потому характеризуется такими же качественными показателями формируемого РЛИ, но требует при реализации почти в два раза меньше памяти при практически том же количестве комплексных умножений.

При необходимости коррекция смещения элементов по дальности и амплитудное взвешивание для уменьшения уровня боковых лепестков могут осуществляться здесь вместе с коррекцией фазы перед объединением сегментов.

Основной трудностью при реализации данного алгоритма впрочем, также как и базового, является необходимость вычисления для каждого нового отсчета РЛИ коэффициентов обработки , и . Всего потребуется определить 2M коэффициентов для всех каналов дальности, обрабатываемых одной фокусирующей функцией.

Количество коэффициентов обработки можно сократить до M + 2 перенеся не зависящие от переменной l значения аргументов входного и корректирующих коэффициентов в аргумент коэффициентов фазовой коррекции и обратного гетеродинирования:

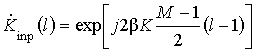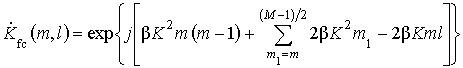. (4)

Дальнейшие модификации алгоритма [3] основаны на том, что в коэффициентах сумма первого и второго слагаемых в показателе экспоненты не зависит от m и равна . Этот постоянный фазовый множитель можно вынести за знак суммы и модуля в выражении (1). Поскольку он влияет только на фазу текущего выходного отсчета РЛИ, то операцию второго этапа обработки можно записать в виде:

, (5)

где .

Особенностью измененных коэффициентов второго этапа обработки является то, что они образуют комплексно сопряженные пары для сегментов, симметрично расположенных относительно центра апертуры. Использование этого свойства коэффициентов позволяет организовать второй этап обработки, например, при нечетном числе сегментов в виде

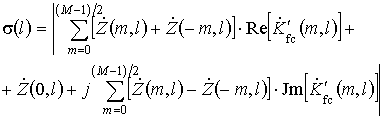(6)

(рис. 4). Количество операций комплексного умножения здесь сокращается приблизительно до 1,5M , а операций вычисления коэффициентов до M /2 + 2 на один выходной отсчет.

Третий вариант модифицированного алгоритма кусочно-линейной аппроксимации получается при перенумеровывании сегментов i = 0…M-1. При этом аргументы коэффициентов фазовой коррекции и обратного гетеродинирования можно представить как

, (7)

а сами коэффициенты, при рекуррентном вычислении, в виде:

(8)

где .

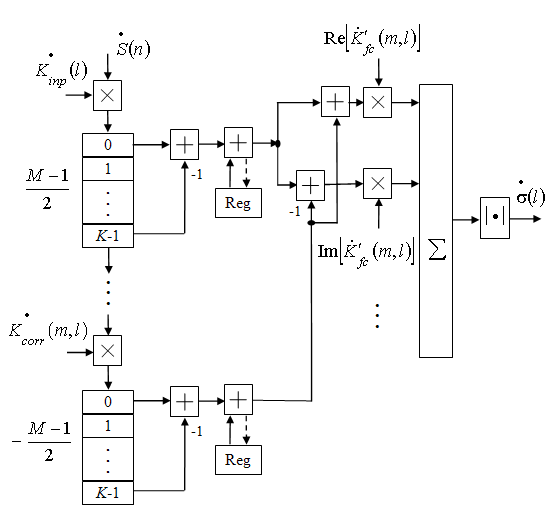
Рис. 4. Структура второго модифицированного алгоритма кусочно-линейной аппроксимации.

Первый множитель данного соотношения при подстановке (8) в выражение (5) можно вынести за знак модуля. Вычисления на втором этапе обработки при этом могут быть организованы следующим образом:

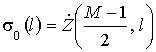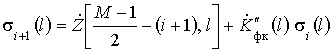. (9)

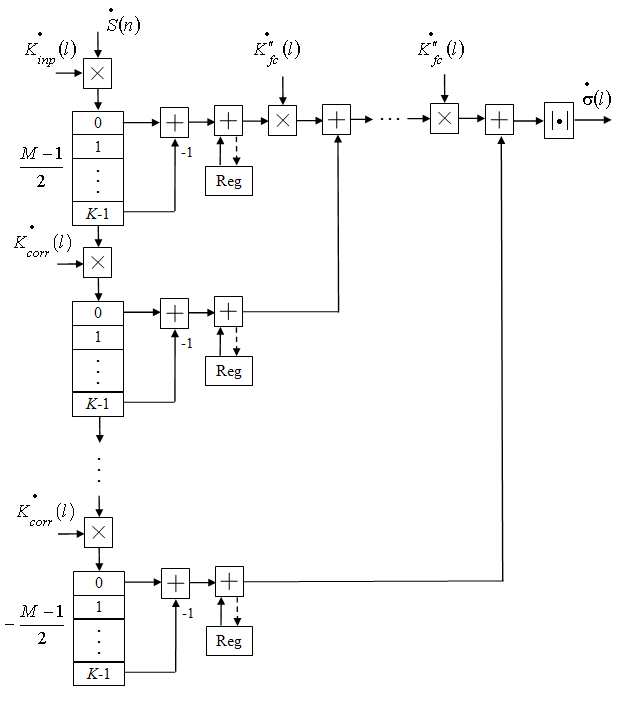
Рис. 5. Структура третьего модифицированного алгоритма кусочно-линейной аппроксимации.

Хотя в этой модификации (рис. 5) количество комплексных умножений (2M-1) немного больше, чем в предыдущей (1,5M), количество вычисляемых

коэффициентов обработки для каждого нового отсчета здесь всего три. Кроме этого, при разработке спецвычислителя, второй этап алгоритма можно выполнить на одной микросхеме, реализующей операцию типа D = C + AB.

3. Анализ алгоритмов кусочно-линейной аппроксимации

Как уже отмечалось, в алгоритмах кусочно-линейной аппроксимации по сравнению с традиционными необходимо рассчитывать коэффициенты обработки для каждого нового отсчета РЛИ. Хотя коэффициенты обработки периодичны по l, их период зависит от наклонной дальности, входящей в , и достаточно велик вследствие нецелочисленного значения величин , . В этой связи предлагается вместо прямого вычисления коэффициентов обработки перейти к таблице, элементами которой являются квантованные значения синуса и косинуса. Кроме этого аргументы коэффициентов определяются рекуррентно и квантуются в диапазоне на N₁ уровней (N₁ – размер таблицы) для определения номера требуемого коэффициента в таблице. Все это позволяет существенно уменьшить временные затраты на их вычисление.

Результаты сравнения алгоритмов кусочно-линейной аппроксимации –базового (КЛА), первого (МКЛА₁), второго (МКЛА₂) и третьего (МКЛА₃), модифицированных с алгоритмом дискретной свертки при формировании пикселя РЛИ в одном канале дальности (без учета входного и выходного буферов для хранения данных), приведены в таблице 1.

При сравнении алгоритмов следует иметь в виду то, что разработанные алгоритмы являются приближенными, а потому сравнение их с алгоритмом дискретной свертки может производиться только после определения их параметров (количества отсчетов в сегменте K и количества сегментов M), влияющих на качественные характеристики синтезируемой апертуры. Основными характеристиками качества формируемого по данным космического РСА радиолокационного изображения являются разрешающая способность и динамический диапазон. Они, в свою очередь, определяются такими характеристиками диаграммы направленности синтезированной антенны как ширина и уровень главного лепестка, а также максимальный и интегральный уровни боковых. Эти характеристики зависят как от параметров РСА, так и от алгоритмов обработки и параметров применяемого вычислителя (разрядности и типа арифметики).

Таблица 1.

Алгоритм	Комплексных умножений	Комплексных сложений	ОЗУ (комплексных слов)	Вычисляемых номеров коэффициентов
1. Дискретной свертки	N	N-1	N	–
2. КЛА	2(M-1)	N-1	2N-K	2M
3. МКЛА₁	2M	3M-1	N+M	2M
4. МКЛА₂	1,5M	3M-1	N+M	2+M/2
5. МКЛА₃	2M-1	3M-1	N+M	3

Исследование эффективности алгоритмов цифровой обработки сигналов вследствие их сложности было проведено методом моделирования на универсальной ЭВМ. Разработанные алгоритмы включают алгоритмы имитации сигналов, отраженных от точечной и протяженной целей и принятых РСА, алгоритмы моделирования процесса цифрового формирования РЛИ с учетом ограниченной разрядности вычислителя и алгоритмы обработки результатов.

Как было показано по результатам моделирования, вполне удовлетворительные характеристики формируемого изображения достигаются при ошибке аппроксимации фазы траекторного сигнала на краю сегмента (таблица 2). При этом с учетом соотношения между максимальной ошибкой аппроксимации и количеством сегментов

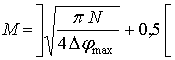(11)

выигрыш в количестве выполняемых комплексных умножений при синтезировании апертуры из 2048 отсчетов для разработанных алгоритмов может достигать почти 30 раз.

В таблице приведены нормированные к номинальным (соответствующим идеальной обработке) значения для уровня главного лепестка и разрешающей способности .

Таблица 2.

Алгоритм

Амплитудный вес

Характеристики ДНСА

дБ

Дискретной

свертки

нет

по апертуре

-1,8

–

-10

-14,5

1,3

Кусочно-линейной аппроксимации

нет

между сегментами

-0,25

-2,0

-15,8

-8

-10,2

1,3

При исследовании требуемой разрядности вычислительного устройства анализировались те же указанные выше параметры диаграммы направленности синтезированной антенны. Анализ требуемой разрядности вычислений проведен методом математического моделирования на ЭВМ процессов, происходящих в исследуемых цифровых фильтрах. При этом исследовалось влияние разрядности сигнала, коэффициентов фильтра и вычислений в арифметике с фиксированной и плавающей запятой. При анализе влияния разрядности вычислений применялась следующая методика: первоначально квантовался только входной сигнал, далее квантовались только коэффициенты обработки. После этого выбирались некоторая разрядность квантования сигнала и коэффициентов обработки, снижающие на малую заданную величину оцениваемые параметры ДНСА, и после этого исследовалась требуемая разрядность вычислителя. Количество отсчетов в синтезированной апертуре при анализе выбрано N = 128 для уменьшения времени вычислений.

При исследовании влияния квантования входного сигнала с округлением на характеристики формируемого изображения показано, что уже при 4-х разрядном АЦП сигнала уровни главного и максимального бокового лепестков отличаются не более чем на 0,3 дБ от соответствующих значений при обработке без квантования, а интегральный уровень боковых лепестков приближается к своему предельному значению, равному - 4,7 дБ (при определении ширины главного лепестка не по нулям диаграммы направленности, а на уровне -3 дБ, поскольку при ограничении разрядности вычислений происходит "заплывание" нулей ДНСА).

По результатам моделирования показано, что при реализации алгоритма дискретной свертки достаточно 16-32 коэффициентов обработки, представляемых 4…5 разрядами, а для алгоритмов кусочно-линейной аппроксимации 32-64 (N/2) коэффициентов при 5 разрядном их представлении.

Требуемая разрядность при вычислениях с фиксированной запятой в алгоритме дискретной свертки определяется разрядностью входного сигнала, поскольку в памяти при реализации этого алгоритма (регистре сдвига) хранятся данные до их умножения на коэффициенты обработки. В модифицированных алгоритмах кусочно- линейной аппроксимации при их реализации необходимо 6...7 разрядов под частичные произведения,для хранения которых требуется основная память и 10...11 разрядов требуется при объединении отсчетов в сегментах.

4. Выводы

Проведено исследование модифицированных алгоритмов кусочно-линейной аппроксимации применительно к обработке сигналов в радиолокаторе с синтезированной апертурой. Определены параметры алгоритмов, определяющие требуемое количество операций при их реализации и качественные характеристики формируемого изображения. Показана высокая вычислительная эффективность данных приближенных алгоритмов по сравнению с алгоритмом дискретной свертки, достигающая 30 раз по количеству комплексных умножений при синтезировании апертуры из 2048 отсчетов. Приведены структурные схемы трех модификаций алгоритма и представлены результаты их анализа по требуемой разрядности вычислений.

Литература

1. Неронский Л.Б., Коберниченко В.Г., Зраенко С.М. Цифровое синтезирование радиолокационных изображений земной поверхности в радиолокаторе с синтезированной апертурой космического аппарата "Алмаз-1" // Исследования Земли из космоса. 1993. №4. С.33-43.

2. Herman E.E., Williams F.C. // Synthetic array processor: Pat. № 4227194. USA. 07.10.80.

3. Зраенко С.М., Коберниченко В.Г. Эффективный алгоритм цифровой обработки сигналов в радиолокаторе с синтезированной апертурой // Цифровые радиоэлектронные системы. 1997. №1. С.22-32.